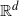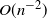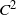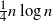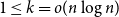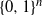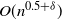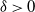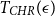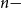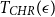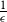135 results
8 - Special Matrices, Markov Chains, and PageRank
-
- Book:
- Linear Algebra for Data Science, Machine Learning, and Signal Processing
- Published online:
- 01 November 2024
- Print publication:
- 16 May 2024, pp 283-334
-
- Chapter
- Export citation

Economic Networks
- Theory and Computation
-
- Published online:
- 11 April 2024
- Print publication:
- 25 April 2024
Topological reconstruction of compact supports of dependent stationary random variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1339-1369
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Perfect sampling of stochastic matching models with reneging
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1307-1339
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
An inaccuracy measure between non-explosive point processes with applications to Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 25 October 2023, pp. 735-756
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
MECHANISTIC MARKOV MODELS FOR THE EVOLUTION OF GENE FAMILIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 10 August 2023, pp. 513-515
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
On Markov chain approximations for computing boundary crossing probabilities of diffusion processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 1386-1415
- Print publication:
- December 2023
-
- Article
- Export citation
Mixing time bounds for edge flipping on regular graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 1317-1332
- Print publication:
- December 2023
-
- Article
- Export citation
Multiple random walks on graphs: mixing few to cover many
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 February 2023, pp. 594-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - The Things that Bug Us*
-
- Book:
- Dicing with Death
- Published online:
- 18 November 2022
- Print publication:
- 08 December 2022, pp 178-205
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Large Deviations for Markov Chains
- Published online:
- 03 August 2022
- Print publication:
- 27 October 2022, pp 1-13
-
- Chapter
- Export citation
Fast mixing of a randomized shift-register Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 253-266
- Print publication:
- March 2023
-
- Article
- Export citation

Large Deviations for Markov Chains
-
- Published online:
- 03 August 2022
- Print publication:
- 27 October 2022
Syllable Structure Spatially Distributed: Patterns of Monosyllables in German Dialects
-
- Journal:
- Journal of Germanic Linguistics / Volume 34 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 01 August 2022, pp. 241-287
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Normal Approximation for Functions of Hidden Markov Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 536-569
- Print publication:
- June 2022
-
- Article
- Export citation
4 - Static Systems: Probabilistic Structural Uncertainty
-
- Book:
- Large-Scale System Analysis Under Uncertainty
- Published online:
- 17 January 2022
- Print publication:
- 17 February 2022, pp 91-129
-
- Chapter
- Export citation
On the forward algorithm for stopping problems on continuous-time Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1043-1063
- Print publication:
- December 2021
-
- Article
- Export citation
On the mixing time of coordinate Hit-and-Run
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 320-332
-
- Article
- Export citation
A product form for the general stochastic matching model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 449-468
- Print publication:
- June 2021
-
- Article
- Export citation
Entropy of killed-resurrected stationary Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 177-196
- Print publication:
- March 2021
-
- Article
- Export citation