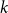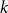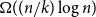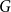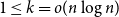1. Introduction
A random walk on a graph is a stochastic process that at each time step chooses a neighbour of the current vertex as its next state. The fact that a random walk visits every vertex of a connected, undirected graph in polynomial time was first used to solve the undirected
![]() $s-t$
connectivity problem in logarithmic space [Reference Aleliunas, Karp, Lipton, Lovász and Rackoff4]. Since then random walks have become a fundamental primitive in the design of randomised algorithms which feature in approximation algorithms and sampling [Reference Lovász44, Reference Sarma, Nanongkai, Pandurangan and Tetali57], load balancing [Reference Karger, Ruhl, Gibbons and Adler35, Reference Sauerwald and Sun59], searching [Reference Gkantsidis, Mihail and Saberi25, Reference Lv, Cao, Cohen, Li, Shenker, Ebcioglu, Pingali and Nicolau45], resource location [Reference Kempe, Kleinberg, Demers, Vitter, Spirakis and Yannakakis36], property testing [Reference Czumaj, Monemizadeh, Onak and Sohler15, Reference Akash Kumar, Stolman and Thorup38, Reference Akash Kumar, Stolman, Charikar and Cohen39], graph parameter estimation [Reference Ben-Hamou, Oliveira, Peres and Czumaj7, Reference Cooper, Radzik and Siantos14] and biological applications [Reference Boczkowski, Guinard, Korman, Lotker, Renault, Bender, Farach-Colton and Mosteiro8, Reference Clementi, D’Amore, Giakkoupis, Natale, Miller, Censor-Hillel and Korhonen10, Reference Guinard, Korman, Paul and Bläser27].
$s-t$
connectivity problem in logarithmic space [Reference Aleliunas, Karp, Lipton, Lovász and Rackoff4]. Since then random walks have become a fundamental primitive in the design of randomised algorithms which feature in approximation algorithms and sampling [Reference Lovász44, Reference Sarma, Nanongkai, Pandurangan and Tetali57], load balancing [Reference Karger, Ruhl, Gibbons and Adler35, Reference Sauerwald and Sun59], searching [Reference Gkantsidis, Mihail and Saberi25, Reference Lv, Cao, Cohen, Li, Shenker, Ebcioglu, Pingali and Nicolau45], resource location [Reference Kempe, Kleinberg, Demers, Vitter, Spirakis and Yannakakis36], property testing [Reference Czumaj, Monemizadeh, Onak and Sohler15, Reference Akash Kumar, Stolman and Thorup38, Reference Akash Kumar, Stolman, Charikar and Cohen39], graph parameter estimation [Reference Ben-Hamou, Oliveira, Peres and Czumaj7, Reference Cooper, Radzik and Siantos14] and biological applications [Reference Boczkowski, Guinard, Korman, Lotker, Renault, Bender, Farach-Colton and Mosteiro8, Reference Clementi, D’Amore, Giakkoupis, Natale, Miller, Censor-Hillel and Korhonen10, Reference Guinard, Korman, Paul and Bläser27].
The fact that random walks are local and memoryless (Markov property) ensures they require very little space and are relatively unaffected by changes in the environment, for example, dynamically evolving graphs or graphs with edge failures. These properties make random walks a natural candidate for parallelisation, where running parallel walks has the potential of lower time overheads. One early instance of this idea are space-time trade-offs for the undirected
![]() $s-t$
connectivity problem [Reference Broder, Karlin, Raghavan and Upfal9, Reference Feige22]. Other applications involving multiple random walks are sublinear algorithms [Reference Czumaj and Sohler16], local clustering [Reference Andersen, Chung and Lang6, Reference Spielman and Teng60] or epidemic processes on networks [Reference Lam, Liu, Mitzenmacher, Sun, Wang and Rabani41, Reference Pettarin, Pietracaprina, Pucci, Upfal, Gavoille and Fraigniaud55].
$s-t$
connectivity problem [Reference Broder, Karlin, Raghavan and Upfal9, Reference Feige22]. Other applications involving multiple random walks are sublinear algorithms [Reference Czumaj and Sohler16], local clustering [Reference Andersen, Chung and Lang6, Reference Spielman and Teng60] or epidemic processes on networks [Reference Lam, Liu, Mitzenmacher, Sun, Wang and Rabani41, Reference Pettarin, Pietracaprina, Pucci, Upfal, Gavoille and Fraigniaud55].
Given the potential applications of multiple random walks in algorithms, it is important to understand fundamental properties of multiple random walks. The speed-up, first introduced in [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5], is the ratio of the worst-case cover time by a single random walk to the cover time of
![]() $k$
parallel walks. Following [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5] and subsequent works [Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Reference Elsässer and Sauerwald20, Reference Ivaskovic, Kosowski, Pajak, Sauerwald, Vollmer and Vallée31, Reference Klasing, Kosowski, Pajak, Sauerwald, Fatourou and Taubenfeld37, Reference Patel, Carron and Bullo53, Reference Sauerwald, Richa and Guerraoui58] our understanding of when and why a speed-up is present has improved. In particular, various results in [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5, Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Reference Elsässer and Sauerwald20] establish that as long as the lengths of the walks are not smaller than the mixing, the speed-up is linear in
$k$
parallel walks. Following [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5] and subsequent works [Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Reference Elsässer and Sauerwald20, Reference Ivaskovic, Kosowski, Pajak, Sauerwald, Vollmer and Vallée31, Reference Klasing, Kosowski, Pajak, Sauerwald, Fatourou and Taubenfeld37, Reference Patel, Carron and Bullo53, Reference Sauerwald, Richa and Guerraoui58] our understanding of when and why a speed-up is present has improved. In particular, various results in [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5, Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Reference Elsässer and Sauerwald20] establish that as long as the lengths of the walks are not smaller than the mixing, the speed-up is linear in
![]() $k$
. However, there are still many challenging open problems, for example, understanding the effect of different start vertices or characterising the magnitude of speed-up in terms of graph properties, a problem already stated in [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5]: ‘
$k$
. However, there are still many challenging open problems, for example, understanding the effect of different start vertices or characterising the magnitude of speed-up in terms of graph properties, a problem already stated in [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5]: ‘
![]() $\ldots$
which leads us to wonder whether there is some other property of a graph that characterises the speed-up achieved by multiple random walks more crisply than hitting and mixing times’. Addressing the previous questions, we introduce new quantities and couplings for multiple random walks, that allow us to improve the state-of-the-art by refining, strengthening or extending results from previous works.
$\ldots$
which leads us to wonder whether there is some other property of a graph that characterises the speed-up achieved by multiple random walks more crisply than hitting and mixing times’. Addressing the previous questions, we introduce new quantities and couplings for multiple random walks, that allow us to improve the state-of-the-art by refining, strengthening or extending results from previous works.
While there is an extensive body of research on the foundations of (single) random walks (and Markov chains), it seems surprisingly hard to transfer these results and develop a systematic theory of multiple random walks. One of the reasons is that processes involving multiple random walks often lead to questions about short random walks, for example, shorter than the mixing time. Such short walks may also arise in applications including generating random walk samples in massively parallel systems [Reference Lacki, Mitrovic, Onak, Sankowski, Makarychev, Makarychev, Tulsiani, Kamath and Chuzhoy40, Reference Sarma, Nanongkai, Pandurangan and Tetali57], or in applications where random walk steps are expensive or subject to delays (e.g. when crawling social networks like Twitter [Reference Cooper, Radzik and Siantos14]). The challenge of analysing short random walks (shorter than mixing or hitting time) has been mentioned not only in the area of multiple cover times (e.g. [Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Sec. 6]), but also in the context of concentration inequalities for random walks [Reference Lezaud43, p. 863] and property testing [Reference Czumaj and Sohler16].
1.1. Our contribution
Our first set of results provide several tight bounds on
![]() $t_{\mathsf{cov}}^{(k)}(\pi )$
in general (connected) graphs, where
$t_{\mathsf{cov}}^{(k)}(\pi )$
in general (connected) graphs, where
![]() $t_{\mathsf{cov}}^{(k)}(\pi )$
is the expected time for each vertex to be visited by at least one of
$t_{\mathsf{cov}}^{(k)}(\pi )$
is the expected time for each vertex to be visited by at least one of
![]() $k$
independent walks each started from a vertex independently sampled from the stationary distribution
$k$
independent walks each started from a vertex independently sampled from the stationary distribution
![]() $\pi$
.
$\pi$
.
The main findings of Section 3 include:
-
Proving general bounds of
 $\mathcal{O} \Bigl ( \bigl (\frac{|E|}{kd_{\mathsf{min}}}\bigr )^2\log ^2 n \Bigr )$
,
$\mathcal{O} \Bigl ( \bigl (\frac{|E|}{kd_{\mathsf{min}}}\bigr )^2\log ^2 n \Bigr )$
,
 $\mathcal{O} \Bigl ( \frac{\max _{v\in V}{\mathbb{E}}_{\pi } \!\left [\tau _v\right ]}{k} \log n \Bigr )$
and
$\mathcal{O} \Bigl ( \frac{\max _{v\in V}{\mathbb{E}}_{\pi } \!\left [\tau _v\right ]}{k} \log n \Bigr )$
and
 $\mathcal{O}\!\left (\frac{|E|\log n}{kd_{\mathsf{min}} \sqrt{1-\lambda _2} }\right )$
on
$\mathcal{O}\!\left (\frac{|E|\log n}{kd_{\mathsf{min}} \sqrt{1-\lambda _2} }\right )$
on
 $t_{\mathsf{cov}}^{(k)}(\pi )$
, where
$t_{\mathsf{cov}}^{(k)}(\pi )$
, where
 $d_{\mathsf{min}}$
is the minimum degree,
$d_{\mathsf{min}}$
is the minimum degree,
 ${\mathbb{E}}_{\pi }\![\tau _v]$
is the hitting time of
${\mathbb{E}}_{\pi }\![\tau _v]$
is the hitting time of
 $v\in V$
from a stationary start vertex and
$v\in V$
from a stationary start vertex and
 $\lambda _2$
is the second largest eigenvalue of the transition matrix of the walk. All three bounds are tight for certain graphs. The first bound improves over [Reference Broder, Karlin, Raghavan and Upfal9], the second result is a Matthew’s type bound for multiple random walks, and the third yields tight bounds for non-regular expanders such as preferential attachment graphs.
$\lambda _2$
is the second largest eigenvalue of the transition matrix of the walk. All three bounds are tight for certain graphs. The first bound improves over [Reference Broder, Karlin, Raghavan and Upfal9], the second result is a Matthew’s type bound for multiple random walks, and the third yields tight bounds for non-regular expanders such as preferential attachment graphs. -
We prove that for any graph
 $G$
and
$G$
and
 $1\leq k= o( n\log n )$
,
$1\leq k= o( n\log n )$
,
 $t_{\mathsf{cov}}^{(k)}(\pi )=\Omega ((n/k) \log n)$
. Weaker versions of this bound were obtained in [Reference Elsässer and Sauerwald20], holding only for certain values of
$t_{\mathsf{cov}}^{(k)}(\pi )=\Omega ((n/k) \log n)$
. Weaker versions of this bound were obtained in [Reference Elsässer and Sauerwald20], holding only for certain values of
 $k$
or under additional assumptions on the mixing time. Our result matches the fundamental
$k$
or under additional assumptions on the mixing time. Our result matches the fundamental
 $\Omega (n \log n)$
lower bound for single random walks (
$\Omega (n \log n)$
lower bound for single random walks (
 $k=1$
) [Reference Aldous3, Reference Feige21], and generalises it in the sense that total amount of work by all
$k=1$
) [Reference Aldous3, Reference Feige21], and generalises it in the sense that total amount of work by all
 $k$
stationary walks together for covering is always
$k$
stationary walks together for covering is always
 $\Omega (n \log n).$
We establish the
$\Omega (n \log n).$
We establish the
 $\Omega ((n/k) \log n)$
bound by reducing the multiple walk process to a single, reversible Markov chain and applying a general lower bound on stationary cover times [Reference Aldous3].
$\Omega ((n/k) \log n)$
bound by reducing the multiple walk process to a single, reversible Markov chain and applying a general lower bound on stationary cover times [Reference Aldous3]. -
A technical tool that provides a bound on the lower tail of the cover time by
 $k$
walks from stationary for graphs with a large and (relatively) symmetric set of hard to hit vertices (Lemma 3.9). When applied to the
$k$
walks from stationary for graphs with a large and (relatively) symmetric set of hard to hit vertices (Lemma 3.9). When applied to the
 $2$
d torus and binary trees this yields a tight lower bound.
$2$
d torus and binary trees this yields a tight lower bound.
In Section 4, we introduce a novel quantity for multiple walks we call partial mixing. Intuitively, instead of mixing all (or at least half) of the
![]() $k$
walks, we only need to mix a specified number
$k$
walks, we only need to mix a specified number
![]() $\tilde{k}$
of them. We put this idea on a more formal footing and prove
$\tilde{k}$
of them. We put this idea on a more formal footing and prove
![]() $\min$
-
$\min$
-
![]() $\max$
theorems which relate worst-case cover times
$\max$
theorems which relate worst-case cover times
![]() $t_{\mathsf{cov}}^{(k)}$
to partial mixing times
$t_{\mathsf{cov}}^{(k)}$
to partial mixing times
![]() $t_{\mathsf{mix}}^{(\tilde{k},k)}$
and stationary cover times:
$t_{\mathsf{mix}}^{(\tilde{k},k)}$
and stationary cover times:
-
For any graph
 $G$
and any
$G$
and any
 $1 \leq k \leq n$
, we prove that:
$1 \leq k \leq n$
, we prove that: \begin{equation*} t_{\mathsf {cov}}^{(k)} \leq 12 \cdot \min _{1 \leq \tilde {k} \lt k} \max \left ( t_{\mathsf {mix}}^{(\tilde {k},k)}, t_{\mathsf {cov}}^{(\tilde {k})}(\pi ) \right ). \end{equation*}
\begin{equation*} t_{\mathsf {cov}}^{(k)} \leq 12 \cdot \min _{1 \leq \tilde {k} \lt k} \max \left ( t_{\mathsf {mix}}^{(\tilde {k},k)}, t_{\mathsf {cov}}^{(\tilde {k})}(\pi ) \right ). \end{equation*}
For now, we omit details such as the definition of the partial mixing time
![]() $t_{\mathsf{mix}}^{(\tilde{k},k)}$
as well as some
$t_{\mathsf{mix}}^{(\tilde{k},k)}$
as well as some
![]() $\min$
-
$\min$
-
![]() $\max$
characterisations that serve as lower bounds (these can be found in Section 4). Intuitively these characterisations suggest that for any number of walks
$\max$
characterisations that serve as lower bounds (these can be found in Section 4). Intuitively these characterisations suggest that for any number of walks
![]() $k$
, there is an ‘optimal’ choice of
$k$
, there is an ‘optimal’ choice of
![]() $\tilde{k}$
so that one first waits until
$\tilde{k}$
so that one first waits until
![]() $\tilde{k}$
out of the
$\tilde{k}$
out of the
![]() $k$
walks are mixed, and then considers only these
$k$
walks are mixed, and then considers only these
![]() $\tilde{k}$
stationary walks when covering the remainder of the graph.
$\tilde{k}$
stationary walks when covering the remainder of the graph.
This argument involving mixing only some walks extends and generalises prior results that involve mixing all (or at least a constant portion) of the
![]() $k$
walks [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5, Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Reference Elsässer and Sauerwald20]. Previous approaches only imply a linear speed-up as long as the lengths of the walks are not shorter than the mixing time of a single random walk. In contrast, our characterisation may still yield tight bounds on the cover time for random walks that are much shorter than the mixing time.
$k$
walks [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5, Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Reference Elsässer and Sauerwald20]. Previous approaches only imply a linear speed-up as long as the lengths of the walks are not shorter than the mixing time of a single random walk. In contrast, our characterisation may still yield tight bounds on the cover time for random walks that are much shorter than the mixing time.
In Section 5, we demonstrate how our insights can be used on several well-known graph classes. As a first step, we determine their stationary cover times; this is based on our bounds from Section 3. Secondly, we derive lower and upper bounds on the partial mixing times. Finally, with the stationary cover times and partial mixing times at hand, we can apply the characterisations from Section 4 to infer lower and upper bounds on the worst-case stationary times. For some of those graphs the worst-case cover times were already known before, while for, e.g., binary trees and preferential attachment graphs, our bounds are new.
-
For the graph families of binary trees, cycles,
 $d$
-dim. tori (
$d$
-dim. tori (
 $d=2$
and
$d=2$
and
 $d\geq 3$
), hypercubes, cliques and (possibly non-regular) expanders we determine the cover time up to constants, for both worst-case and stationary start vertices (see Table 1 for the quantitative results).
$d\geq 3$
), hypercubes, cliques and (possibly non-regular) expanders we determine the cover time up to constants, for both worst-case and stationary start vertices (see Table 1 for the quantitative results).
We believe that this new methodology constitutes some progress towards the open question of Alon, Avin, Koucký, Kozma, Lotker, and Tuttle [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5] concerning a characterisation of worst-case cover times.
Table 1 All results above are
![]() $\Theta(\cdot)$
, that is bounded above and below by a multiplicative constant, apart from the mixing time of expanders which is only bounded from above.
$\Theta(\cdot)$
, that is bounded above and below by a multiplicative constant, apart from the mixing time of expanders which is only bounded from above.

Notes: PA above is the preferential attachment process where each vertex has
![]() $m$
initial links, the results hold w.h.p., see [Reference Cooper and Frieze12, Reference Mihail, Papadimitriou and Saberi48]. Cells shaded in
$m$
initial links, the results hold w.h.p., see [Reference Cooper and Frieze12, Reference Mihail, Papadimitriou and Saberi48]. Cells shaded in ![]() are new results proved in this paper with the exception that for
are new results proved in this paper with the exception that for
![]() $k= \mathcal{O}(\!\log n)$
upper bounds on the stationary cover time for binary trees, expanders and preferential attachment graphs can be deduced from general bounds for the worst-case cover time in [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5]. Cells shaded
$k= \mathcal{O}(\!\log n)$
upper bounds on the stationary cover time for binary trees, expanders and preferential attachment graphs can be deduced from general bounds for the worst-case cover time in [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5]. Cells shaded ![]() in the second to last column are known results we re-prove in this paper using our partial mixing time results, for the
in the second to last column are known results we re-prove in this paper using our partial mixing time results, for the
![]() $2$
-dim grid we only re-prove upper bounds. References for the second to last column are given in Section 5, except for the barbell, see [Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, p. 2]. The barbell consists of two cliques on
$2$
-dim grid we only re-prove upper bounds. References for the second to last column are given in Section 5, except for the barbell, see [Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, p. 2]. The barbell consists of two cliques on
![]() $n/2$
vertices connected by single edge; we include this in the table as an interesting example where the speed-up by stationary walks is exponential in
$n/2$
vertices connected by single edge; we include this in the table as an interesting example where the speed-up by stationary walks is exponential in
![]() $k$
. All other results for single walks can be found in [Reference Aldous and Fill2], for example.
$k$
. All other results for single walks can be found in [Reference Aldous and Fill2], for example.
1.2. Novelty of our techniques
While a lot of the proof techniques in previous work [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5, Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Reference Elsässer and Sauerwald20, Reference Sauerwald, Richa and Guerraoui58] are based on direct arguments such as mixing time (or relaxation time), our work introduces a number of new methods which, to the best of our knowledge, have not been used in the analysis of cover time of multiple walks before. In particular, one important novel concept is the introduction of the so-called partial mixing time. The idea is that instead of waiting for all (or a constant portion of)
![]() $k$
walks to mix, we can just mix some
$k$
walks to mix, we can just mix some
![]() $\tilde{k}\leq k$
walks to reap the benefits of coupling these
$\tilde{k}\leq k$
walks to reap the benefits of coupling these
![]() $\tilde{k}$
walks to stationary walks. This then presents a delicate balancing act where one must find an optimal
$\tilde{k}$
walks to stationary walks. This then presents a delicate balancing act where one must find an optimal
![]() $\tilde{k}$
minimising the overall bound on the cover time, for example in expanders the optimal
$\tilde{k}$
minimising the overall bound on the cover time, for example in expanders the optimal
![]() $\tilde{k}$
is linear in
$\tilde{k}$
is linear in
![]() $k$
whereas in binary trees it is approximately
$k$
whereas in binary trees it is approximately
![]() $\sqrt{k}$
, and for the cycle it is roughly
$\sqrt{k}$
, and for the cycle it is roughly
![]() $\log k$
. This turning point reveals something about the structure of the graph and our results relating partial mixing to hitting time of sets helps one find this. Another tool we frequently use is a reduction to random walks with geometric resets, similar to a PageRank process, which allows us to relate multiple walks from stationary to a single reversible Markov chain.
$\log k$
. This turning point reveals something about the structure of the graph and our results relating partial mixing to hitting time of sets helps one find this. Another tool we frequently use is a reduction to random walks with geometric resets, similar to a PageRank process, which allows us to relate multiple walks from stationary to a single reversible Markov chain.
2. Notation and preliminaries
Throughout
![]() $G=(V,E)$
will be a finite undirected, connected graph with
$G=(V,E)$
will be a finite undirected, connected graph with
![]() $n=|V|$
vertices and
$n=|V|$
vertices and
![]() $m=|E|$
edges. For
$m=|E|$
edges. For
![]() $v\in V(G)$
let
$v\in V(G)$
let
![]() $d(v)=|\{u\in V \;:\; uv\in E(G)\}|$
denote the degree of
$d(v)=|\{u\in V \;:\; uv\in E(G)\}|$
denote the degree of
![]() $v$
and
$v$
and
![]() $d_{\mathsf{min}}= \min _{v \in V}d(v)$
and
$d_{\mathsf{min}}= \min _{v \in V}d(v)$
and
![]() $d_{\mathsf{max}}= \max _{v \in V}d(v)$
denote the minimum and maximum degrees in
$d_{\mathsf{max}}= \max _{v \in V}d(v)$
denote the minimum and maximum degrees in
![]() $G$
respectively. For any
$G$
respectively. For any
![]() $ k \geq 1$
, let
$ k \geq 1$
, let
![]() $X_t= \left(X_t^{(1)},\dots, X_t^{(k)}\right)$
be the multiple random walk process where each
$X_t= \left(X_t^{(1)},\dots, X_t^{(k)}\right)$
be the multiple random walk process where each
![]() $X_{t}^{(i)}$
is an independent random walk on
$X_{t}^{(i)}$
is an independent random walk on
![]() $G$
. Let
$G$
. Let
denote the conditional expectation where, for each
![]() $1\leq i\leq k$
,
$1\leq i\leq k$
,
![]() $X_{0}^{(i)} =u_i\in V$
is the start vertex of the
$X_{0}^{(i)} =u_i\in V$
is the start vertex of the
![]() $i$
th walk. Unless mentioned otherwise, walks will be lazy, that is, at each step the walk stays at its current location with probability
$i$
th walk. Unless mentioned otherwise, walks will be lazy, that is, at each step the walk stays at its current location with probability
![]() $1/2$
, and otherwise moves to a neighbour chosen uniformly at random. We let the random variable
$1/2$
, and otherwise moves to a neighbour chosen uniformly at random. We let the random variable
![]() $\tau _{\mathsf{cov}}^{(k)}(G)=\inf \!\left\{t \;:\; \bigcup _{i=0}^t\{X_i^{(1)}, \dots, X_i^{(k)} \} = V \right\}$
be the first time every vertex of the graph has been visited by some walk
$\tau _{\mathsf{cov}}^{(k)}(G)=\inf \!\left\{t \;:\; \bigcup _{i=0}^t\{X_i^{(1)}, \dots, X_i^{(k)} \} = V \right\}$
be the first time every vertex of the graph has been visited by some walk
![]() $X_t^{(i)}$
. For
$X_t^{(i)}$
. For
![]() $u_1, \dots, u_k\in V$
let
$u_1, \dots, u_k\in V$
let
denote the cover time of
![]() $k$
walks from
$k$
walks from
![]() $(u_1, \dots, u_k)$
and the cover time of
$(u_1, \dots, u_k)$
and the cover time of
![]() $k$
walks from worst-case start positions respectively. For simplicity, we drop
$k$
walks from worst-case start positions respectively. For simplicity, we drop
![]() $G$
from the notation if the underlying graph is clear from the context. We shall use
$G$
from the notation if the underlying graph is clear from the context. We shall use
![]() $\pi$
to denote the stationary distribution of a single random walk on a graph
$\pi$
to denote the stationary distribution of a single random walk on a graph
![]() $G$
. For
$G$
. For
![]() $v\in V$
this is given by
$v\in V$
this is given by
![]() $\pi (v) = \frac{d(v)}{ 2m}$
which is the degree over twice the number of edges. Let
$\pi (v) = \frac{d(v)}{ 2m}$
which is the degree over twice the number of edges. Let
![]() $\pi _{\min } = \min _{v\in V} \pi (v)$
and
$\pi _{\min } = \min _{v\in V} \pi (v)$
and
![]() $\pi _{\max }=\max _{v\in V} \pi (v)$
. We use
$\pi _{\max }=\max _{v\in V} \pi (v)$
. We use
![]() $\pi ^k$
, which is a distribution on
$\pi ^k$
, which is a distribution on
![]() $V^k$
given by the product measure of
$V^k$
given by the product measure of
![]() $\pi$
with itself, to denote the stationary distribution of a multiple random walk. For a probability distribution
$\pi$
with itself, to denote the stationary distribution of a multiple random walk. For a probability distribution
![]() $\mu$
on
$\mu$
on
![]() $V$
let
$V$
let
![]() ${\mathbb{E}}_{\mu ^k} [\!\cdot\!]$
denote the expectation with respect to
${\mathbb{E}}_{\mu ^k} [\!\cdot\!]$
denote the expectation with respect to
![]() $k$
walks where each start vertex is sampled independently from
$k$
walks where each start vertex is sampled independently from
![]() $\mu$
and
$\mu$
and
In particular,
![]() $t_{\mathsf{cov}}^{(k)}(\pi,G)$
denotes the expected cover time from
$t_{\mathsf{cov}}^{(k)}(\pi,G)$
denotes the expected cover time from
![]() $k$
independent stationary start vertices. For a set
$k$
independent stationary start vertices. For a set
![]() $S\subseteq V$
(if
$S\subseteq V$
(if
![]() $S=\{v\}$
is a singleton set we use
$S=\{v\}$
is a singleton set we use
![]() $\tau _v^{(k)}$
, dropping brackets), we define
$\tau _v^{(k)}$
, dropping brackets), we define
as the first time at least one vertex in the set
![]() $S$
is visited by any of the
$S$
is visited by any of the
![]() $k$
independent random walks. Let
$k$
independent random walks. Let
be the worst-case vertex to vertex hitting time. When talking about a single random walk we drop the (1) index, that is,
![]() $t_{\mathsf{cov}}^{(1)}(G) = t_{\mathsf{cov}}(G)$
; we also drop
$t_{\mathsf{cov}}^{(1)}(G) = t_{\mathsf{cov}}(G)$
; we also drop
![]() $G$
from the notation when the graph is clear. If we wish the graph
$G$
from the notation when the graph is clear. If we wish the graph
![]() $G$
to be clear we shall also use the notation
$G$
to be clear we shall also use the notation
![]() ${\mathbb{P}}_{u,G}[ \cdot ]$
and
${\mathbb{P}}_{u,G}[ \cdot ]$
and
![]() ${\mathbb{E}}_{u,G} [ \cdot ]$
. For
${\mathbb{E}}_{u,G} [ \cdot ]$
. For
![]() $t\geq 0$
we let
$t\geq 0$
we let
![]() $N_v(t)$
denote the number of visits to
$N_v(t)$
denote the number of visits to
![]() $v\in V$
by a single random walk up-to time
$v\in V$
by a single random walk up-to time
![]() $t$
.
$t$
.
For a single random walk
![]() $X_t$
with stationary distribution
$X_t$
with stationary distribution
![]() $\pi$
and
$\pi$
and
![]() $x\in V$
, let
$x\in V$
, let
![]() $d_{\textrm{TV}}(t)$
and
$d_{\textrm{TV}}(t)$
and
![]() $s_x(t)$
be the total variation and separation distances for
$s_x(t)$
be the total variation and separation distances for
![]() $X_t$
given by
$X_t$
given by
where
![]() $P_{x,\cdot }^t$
is the
$P_{x,\cdot }^t$
is the
![]() $t$
-step probability distribution of a random walk starting from
$t$
-step probability distribution of a random walk starting from
![]() $x$
and, for probability measures
$x$
and, for probability measures
![]() $\mu,\nu$
,
$\mu,\nu$
,
![]() $||\mu - \nu ||_{\textrm{TV}} = \frac{1}{2}\sum _{x\in V}|\mu (x)-\nu (x)|$
is the total variation distance. Let
$||\mu - \nu ||_{\textrm{TV}} = \frac{1}{2}\sum _{x\in V}|\mu (x)-\nu (x)|$
is the total variation distance. Let
![]() $ s(t)=\max _{x\in V}s_x(t)$
, then for
$ s(t)=\max _{x\in V}s_x(t)$
, then for
![]() $0\lt \varepsilon \leq 1$
the mixing and separation times [Reference Levin, Peres and Wilmer42, (4.32)] are
$0\lt \varepsilon \leq 1$
the mixing and separation times [Reference Levin, Peres and Wilmer42, (4.32)] are
and
![]() $t_{\mathsf{mix}}\;:\!=\;t_{\mathsf{mix}}(1/4)$
and
$t_{\mathsf{mix}}\;:\!=\;t_{\mathsf{mix}}(1/4)$
and
![]() $t_{\mathsf{sep}}\;:\!=\; t_{\mathsf{sep}}(1/e)$
. A strong stationary time (SST)
$t_{\mathsf{sep}}\;:\!=\; t_{\mathsf{sep}}(1/e)$
. A strong stationary time (SST)
![]() $\sigma$
, see [Reference Levin, Peres and Wilmer42, Ch. 6] or [Reference Aldous and Diaconis1], is a randomised stopping time for a Markov chain
$\sigma$
, see [Reference Levin, Peres and Wilmer42, Ch. 6] or [Reference Aldous and Diaconis1], is a randomised stopping time for a Markov chain
![]() $Y_t$
on
$Y_t$
on
![]() $V$
with stationary distribution
$V$
with stationary distribution
![]() $\pi$
if
$\pi$
if
Let
![]() $t_{\mathsf{rel}} = \frac{1}{1-\lambda _2}$
be the relaxation time of
$t_{\mathsf{rel}} = \frac{1}{1-\lambda _2}$
be the relaxation time of
![]() $G$
, where
$G$
, where
![]() $\lambda _2$
is the second largest eigenvalue of the transition matrix of the (lazy) random walk on
$\lambda _2$
is the second largest eigenvalue of the transition matrix of the (lazy) random walk on
![]() $G$
. A sequence of graphs
$G$
. A sequence of graphs
![]() $(G_n)$
is a sequence of expanders (or simply an expander) if
$(G_n)$
is a sequence of expanders (or simply an expander) if
![]() $\liminf _{n\to \infty } 1-\lambda _2(G_n) \gt 0$
, which implies that
$\liminf _{n\to \infty } 1-\lambda _2(G_n) \gt 0$
, which implies that
![]() $t_{\mathsf{rel}} = \Theta (1)$
.
$t_{\mathsf{rel}} = \Theta (1)$
.
For random variables
![]() $Y,Z$
we say that
$Y,Z$
we say that
![]() $Y$
dominates
$Y$
dominates
![]() $Z$
(
$Z$
(
![]() $Y\succeq Z$
) if
$Y\succeq Z$
) if
![]() $ {\mathbb{P}} [ Y \geq x ] \geq {\mathbb{P}} [ Z \geq x ]$
for all real
$ {\mathbb{P}} [ Y \geq x ] \geq {\mathbb{P}} [ Z \geq x ]$
for all real
![]() $x$
. Finally, we shall use the following inequality [Reference Motwani and Raghavan50, Proposition B.3]:
$x$
. Finally, we shall use the following inequality [Reference Motwani and Raghavan50, Proposition B.3]:
3. Multiple stationary cover times
We shall state our general upper and lower bound results for multiple walks from stationary in Sections 3.1 and 3.2 before proving these results in Sections 3.3 and 3.4, respectively.
3.1. Upper bounds
Broder, Karlin, Raghavan and Upfal [Reference Broder, Karlin, Raghavan and Upfal9] showed that for any graph
![]() $G$
(with
$G$
(with
![]() $m=|E|$
) and
$m=|E|$
) and
![]() $k\geq 1$
,
$k\geq 1$
,
We first prove a general bound which improves this bound by a multiplicative factor of
![]() $d_{\mathsf{min}} ^2\log n$
which may be
$d_{\mathsf{min}} ^2\log n$
which may be
![]() $\Theta (n^2\log n)$
for some graphs.
$\Theta (n^2\log n)$
for some graphs.
Theorem 3.1.
For any graph
![]() $G$
and any
$G$
and any
![]() $k\geq 1$
,
$k\geq 1$
,
This bound is tight for the cycle if
![]() $k=n^{\Theta (1)}$
, see Theorem 5.2. Theorem 3.1 is proved by relating the probability a vertex
$k=n^{\Theta (1)}$
, see Theorem 5.2. Theorem 3.1 is proved by relating the probability a vertex
![]() $v$
is not hit up to a certain time
$v$
is not hit up to a certain time
![]() $t$
to the expected number of returns to
$t$
to the expected number of returns to
![]() $v$
by a walk of length
$v$
by a walk of length
![]() $t$
from
$t$
from
![]() $v$
and applying a bound by Oliveira and Peres [Reference Oliveira, Peres, Mishna and Munro51].
$v$
and applying a bound by Oliveira and Peres [Reference Oliveira, Peres, Mishna and Munro51].
The next bound is analogous to Matthew’s bound [Reference Aldous and Fill2, Theorem 2.26] for the cover time of single random walks from worst-case, however it is proved by a different method.
Theorem 3.2.
For any graph
![]() $G$
and any
$G$
and any
![]() $k\geq 1$
, we have
$k\geq 1$
, we have
This bound is tight for many graphs, see Table 1. Following this paper the stronger bound
![]() $t_{\mathsf{cov}}^{(k)}(\pi ) = \mathcal{O}(t_{\mathsf{cov}}/k )$
was recently proved by Hermon and Sousi [Reference Hermon and Sousi30]. A version of Theorem 3.2 for
$t_{\mathsf{cov}}^{(k)}(\pi ) = \mathcal{O}(t_{\mathsf{cov}}/k )$
was recently proved by Hermon and Sousi [Reference Hermon and Sousi30]. A version of Theorem 3.2 for
![]() $t_{\mathsf{cov}}^{(k)}$
was established in [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5] provided
$t_{\mathsf{cov}}^{(k)}$
was established in [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5] provided
![]() $k=\mathcal{O}(\!\log n )$
, the restriction on
$k=\mathcal{O}(\!\log n )$
, the restriction on
![]() $k$
is necessary (for worst-case) as witnessed by the cycle. Theorem 3.2 also gives the following explicit bound.
$k$
is necessary (for worst-case) as witnessed by the cycle. Theorem 3.2 also gives the following explicit bound.
Corollary 3.3.
For any graph
![]() $G$
and any
$G$
and any
![]() $k\geq 1$
, we have
$k\geq 1$
, we have
Proof. Use
![]() $\max _{v\in V}{\mathbb{E}}_{\pi } [\tau _{v}] \leq 20 m \sqrt{t_{\mathsf{rel}}+1}/d_{\mathsf{min}}$
from [Reference Oliveira, Peres, Mishna and Munro51, Theorem 1] in Theorem 3.2.
$\max _{v\in V}{\mathbb{E}}_{\pi } [\tau _{v}] \leq 20 m \sqrt{t_{\mathsf{rel}}+1}/d_{\mathsf{min}}$
from [Reference Oliveira, Peres, Mishna and Munro51, Theorem 1] in Theorem 3.2.
Notice that, for any
![]() $k\geq 1$
, this bound is tight for any expander with
$k\geq 1$
, this bound is tight for any expander with
![]() $d_{\min }=\Omega (m/n)$
, such as preferential attachment graphs with
$d_{\min }=\Omega (m/n)$
, such as preferential attachment graphs with
![]() $m\geq 2$
, see Theorems 5.14 and 5.13. We now establish some bounds for classes of graphs determined by the return probabilities of random walks.
$m\geq 2$
, see Theorems 5.14 and 5.13. We now establish some bounds for classes of graphs determined by the return probabilities of random walks.
Lemma 3.4.
Let
![]() $G$
be any graph satisfying
$G$
be any graph satisfying
![]() $\pi _{\mathsf{min}} =\Omega (1/n)$
,
$\pi _{\mathsf{min}} =\Omega (1/n)$
,
![]() $t_{\mathsf{mix}} = \mathcal{O}(n )$
and
$t_{\mathsf{mix}} = \mathcal{O}(n )$
and
![]() $\sum _{i=0}^{t} P_{vv}^i =\mathcal{O}(1 + t\pi (v) )$
for any
$\sum _{i=0}^{t} P_{vv}^i =\mathcal{O}(1 + t\pi (v) )$
for any
![]() $t\leq t_{\mathsf{rel}}$
and
$t\leq t_{\mathsf{rel}}$
and
![]() $v\in V$
. Then for any
$v\in V$
. Then for any
![]() $1\leq k\leq n$
,
$1\leq k\leq n$
,
The bound above applies to a broad class of graphs including the hypercube and high dimensional grids. The following bound holds for graphs with sub-harmonic return times, this includes binary trees and
![]() $2$
d-grid/torus.
$2$
d-grid/torus.
Lemma 3.5.
Let
![]() $G$
be any graph satisfying
$G$
be any graph satisfying
![]() $\pi _{\max } =\mathcal{O}(\pi _{\min } )$
,
$\pi _{\max } =\mathcal{O}(\pi _{\min } )$
,
![]() $\sum _{i=0}^tP_{v,v}^i = \mathcal{O}(1+\log t )$
for any
$\sum _{i=0}^tP_{v,v}^i = \mathcal{O}(1+\log t )$
for any
![]() $t\leq t_{\mathsf{rel}}$
and
$t\leq t_{\mathsf{rel}}$
and
![]() $v\in V$
, and
$v\in V$
, and
![]() $t_{\mathsf{mix}}=\mathcal{O}(n )$
. Then for any
$t_{\mathsf{mix}}=\mathcal{O}(n )$
. Then for any
![]() $1\leq k\leq (n\log n)/3$
,
$1\leq k\leq (n\log n)/3$
,
3.2. Lower bounds
Generally speaking, lower bounds for random walks seem to be somewhat more challenging to derive than upper bounds. In particular, the problem of obtaining a tight lower bound for the cover time of a simple random walk on an undirected graph was open for many years [Reference Aldous and Fill2]. This was finally resolved by Feige [Reference Feige21] who proved
![]() $t_{\mathsf{cov}} \geq (1-o(1 ))n\log n$
(this bound was known up-to constants for stationary Markov chains by Aldous [Reference Aldous3]). We prove a generalisation of this bound, up to constants, that holds for
$t_{\mathsf{cov}} \geq (1-o(1 ))n\log n$
(this bound was known up-to constants for stationary Markov chains by Aldous [Reference Aldous3]). We prove a generalisation of this bound, up to constants, that holds for
![]() $k$
random walks starting from stationary (thus also for worst-case).
$k$
random walks starting from stationary (thus also for worst-case).
Theorem 3.6.
There exists a constant
![]() $c\gt 0$
such that for any graph
$c\gt 0$
such that for any graph
![]() $G$
and
$G$
and
![]() $1 \leq k \leq c \cdot n\log n$
,
$1 \leq k \leq c \cdot n\log n$
,
We remark that in this section all results hold (and are proven) for non-lazy random walks, which by stochastic domination implies that the same result also holds for lazy random walks. Theorem 3.6 is tight, uniformly for all
![]() $1 \leq k \leq n$
, for the hypercube, expanders and high-dimensional tori, see Theorem 5.14. We note that [Reference Elsässer and Sauerwald20] proved this bound for any start vertices under the additional assumption that
$1 \leq k \leq n$
, for the hypercube, expanders and high-dimensional tori, see Theorem 5.14. We note that [Reference Elsässer and Sauerwald20] proved this bound for any start vertices under the additional assumption that
![]() $k \geq n^{\epsilon }$
, for some constant
$k \geq n^{\epsilon }$
, for some constant
![]() $\varepsilon \gt 0$
. One can track the constants in the proof of Theorem 3.6 and show that
$\varepsilon \gt 0$
. One can track the constants in the proof of Theorem 3.6 and show that
![]() $c \gt 2 \cdot 10^{-11}$
, we have not optimised this but note that
$c \gt 2 \cdot 10^{-11}$
, we have not optimised this but note that
![]() $c\leq 1$
must hold in either condition of Theorem 3.6 due to the complete graph.
$c\leq 1$
must hold in either condition of Theorem 3.6 due to the complete graph.
To prove this result, we introduce the geometric reset graph, which allows us to couple the multiple random walk to a single walk to which we can apply a lower bound by Aldous [Reference Aldous3]. The geometric reset graph is a small modification to a graph
![]() $G$
which gives an edge-weighted graph
$G$
which gives an edge-weighted graph
![]() $\widehat{G}(x)$
such that the simple random walk on
$\widehat{G}(x)$
such that the simple random walk on
![]() $\widehat{G}(x)$
emulates a random walk on
$\widehat{G}(x)$
emulates a random walk on
![]() $G$
with
$G$
with
![]() $\operatorname{Geo}\!(x )$
resets to stationarity, where
$\operatorname{Geo}\!(x )$
resets to stationarity, where
![]() $\operatorname{Geo}(x )$
is a geometric random variable with expectation
$\operatorname{Geo}(x )$
is a geometric random variable with expectation
![]() $1/x$
. This is achieved by adding a dominating vertex
$1/x$
. This is achieved by adding a dominating vertex
![]() $z$
to the graph and weighting edges from
$z$
to the graph and weighting edges from
![]() $z$
so that after
$z$
so that after
![]() $z$
is visited the walk moves to a vertex
$z$
is visited the walk moves to a vertex
![]() $v\in V(G)$
proportional with probability
$v\in V(G)$
proportional with probability
![]() $\pi (v)$
.
$\pi (v)$
.
Definition 3.7.
(The Geometric Reset Graph
![]() $\widehat{G}(x)$
). For any graph
$\widehat{G}(x)$
). For any graph
![]() $G$
the undirected, edge-weighted graph
$G$
the undirected, edge-weighted graph
![]() $\widehat{G}(x)$
, where
$\widehat{G}(x)$
, where
![]() $0 \lt x \leq 1$
, consists of all vertices
$0 \lt x \leq 1$
, consists of all vertices
![]() $V(G)$
and one extra vertex
$V(G)$
and one extra vertex
![]() $z$
. All edges from
$z$
. All edges from
![]() $G$
are included with edge-weight
$G$
are included with edge-weight
![]() $1-x$
. Further,
$1-x$
. Further,
![]() $z$
is connected to each vertex
$z$
is connected to each vertex
![]() $u \in G$
by an edge with edge-weight
$u \in G$
by an edge with edge-weight
![]() $x \cdot d(u)$
, where
$x \cdot d(u)$
, where
![]() $d(u)$
is the degree of vertex
$d(u)$
is the degree of vertex
![]() $u$
in
$u$
in
![]() $G$
.
$G$
.
Given a graph with edge weights
![]() $\{w_e\}_{e\in E}$
the probability a non-lazy random walk moves from
$\{w_e\}_{e\in E}$
the probability a non-lazy random walk moves from
![]() $u$
to
$u$
to
![]() $v$
is given by
$v$
is given by
![]() $w_{uv}/ \sum _{w\in V} w_{uw}$
. Thus the walk on
$w_{uv}/ \sum _{w\in V} w_{uw}$
. Thus the walk on
![]() $\widehat{G}(x)$
behaves as a random walk in
$\widehat{G}(x)$
behaves as a random walk in
![]() $G$
, apart from that in any step, it may move to the extra vertex
$G$
, apart from that in any step, it may move to the extra vertex
![]() $z$
with probability
$z$
with probability
![]() $\frac{x d(u)}{x d(u) + (1-x)d(u)} = x$
. Once the walk is at
$\frac{x d(u)}{x d(u) + (1-x)d(u)} = x$
. Once the walk is at
![]() $z$
it moves back to a vertex
$z$
it moves back to a vertex
![]() $u \in V\backslash \{z\}$
with probability
$u \in V\backslash \{z\}$
with probability
Hence, the stationary distribution
![]() $\widehat{\pi }$
of the random walk on
$\widehat{\pi }$
of the random walk on
![]() $\widehat{G}(x)$
is proportional to
$\widehat{G}(x)$
is proportional to
![]() $\pi$
on
$\pi$
on
![]() $V(G)$
, and for the extra vertex
$V(G)$
, and for the extra vertex
![]() $z$
we have
$z$
we have
Using the next lemma, we can then obtain bounds on the multiple stationary cover time by simply bounding the cover time in the augmented graph
![]() $\widehat{G}(x)$
for some
$\widehat{G}(x)$
for some
![]() $x$
.
$x$
.
Lemma 3.8.
Let
![]() $G$
be any graph,
$G$
be any graph,
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $x = Ck/T$
where
$x = Ck/T$
where
![]() $C\gt 30$
and
$C\gt 30$
and
![]() $T\geq 5Ck$
. Then,
$T\geq 5Ck$
. Then,
The result in Lemma 3.8 will also be used later in this work to prove a lower bound for the stationary cover time of the binary tree and two-dimensional grid when
![]() $k$
is small.
$k$
is small.
The next result we present utilises the second moment method to obtain a lower bound which works well for
![]() $k=n^{\Theta (1)}$
walks on symmetric (e.g. transitive) graphs. In particular, we apply this to get tight lower bounds for cycles, the
$k=n^{\Theta (1)}$
walks on symmetric (e.g. transitive) graphs. In particular, we apply this to get tight lower bounds for cycles, the
![]() $2$
-dim. torus and binary trees in Section 5.
$2$
-dim. torus and binary trees in Section 5.
Lemma 3.9.
For any graph
![]() $G$
, subset
$G$
, subset
![]() $S\subseteq V$
and
$S\subseteq V$
and
![]() $t\geq 1$
, let
$t\geq 1$
, let
![]() $p = \max _{u\in S}{\mathbb{P}}_{\pi }[\tau _u\leq t ]$
. Then, for any
$p = \max _{u\in S}{\mathbb{P}}_{\pi }[\tau _u\leq t ]$
. Then, for any
![]() $k\geq 2$
satisfying
$k\geq 2$
satisfying
![]() $ 2p^2k\lt 1$
, we have
$ 2p^2k\lt 1$
, we have
3.3. Proofs of upper bounds
We begin by stating some basic facts.
Lemma 3.10.
Let
![]() $N_v(t)$
be the number of visits to
$N_v(t)$
be the number of visits to
![]() $v\in V$
by a
$v\in V$
by a
![]() $t$
-step walk,
$t$
-step walk,
![]() $t\geq 1$
, then
$t\geq 1$
, then
-
(i)
 $\displaystyle {\mathbb{P}}_{\pi ^k}\!\left[\tau _{\mathsf{cov}}^{(k)} \geq t \right] \leq \sum _{v\in V}\exp\!(\!-\!k{\mathbb{P}}_{\pi }[N_v(t)\geq 1 ] ),$
$\displaystyle {\mathbb{P}}_{\pi ^k}\!\left[\tau _{\mathsf{cov}}^{(k)} \geq t \right] \leq \sum _{v\in V}\exp\!(\!-\!k{\mathbb{P}}_{\pi }[N_v(t)\geq 1 ] ),$
-
(ii)
 $\displaystyle \frac{(t+1)\pi (v)}{\sum _{i=0}^tP_{v,v}^{i}}\leq {\mathbb{P}}_{\pi }\!\left [N_v(t)\geq 1 \right ] =\frac{{\mathbb{E}}_{\pi } \!\left [N_v(t)\right ]}{{\mathbb{E}}_{\pi } \!\left [N_v(t)\mid N_v(t)\geq 1\right ]} \leq \frac{2(t+1)\pi (v)}{ \sum _{i=0}^{t/2} P_{v,v}^i }$
,
$\displaystyle \frac{(t+1)\pi (v)}{\sum _{i=0}^tP_{v,v}^{i}}\leq {\mathbb{P}}_{\pi }\!\left [N_v(t)\geq 1 \right ] =\frac{{\mathbb{E}}_{\pi } \!\left [N_v(t)\right ]}{{\mathbb{E}}_{\pi } \!\left [N_v(t)\mid N_v(t)\geq 1\right ]} \leq \frac{2(t+1)\pi (v)}{ \sum _{i=0}^{t/2} P_{v,v}^i }$
, -
(iii)
 $\displaystyle \sum _{i=0}^tP_{u,u}^{i} \leq \frac{e}{e-1}\left (\sum _{i=0}^{\lceil t_{\mathsf{rel}} \rceil -1}P_{u,u}^{i} -\lceil t_{\mathsf{rel}} \rceil \pi (u)\right )+ (t+1)\pi (u)$
.
$\displaystyle \sum _{i=0}^tP_{u,u}^{i} \leq \frac{e}{e-1}\left (\sum _{i=0}^{\lceil t_{\mathsf{rel}} \rceil -1}P_{u,u}^{i} -\lceil t_{\mathsf{rel}} \rceil \pi (u)\right )+ (t+1)\pi (u)$
.
Proof. For Item (i), by independence of the walks and the union bound we have
 \begin{align*} {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)} \geq t \right ] & \leq \sum _{v\in V} \prod _{i=1}^k\left (1-{\mathbb{P}}_{\pi }\!\left [N_v^{(i)}(t)\geq 1\right ]\right )\leq \sum _{v\in V}\exp\!\left (-k{\mathbb{P}}_{\pi }\!\left [N_v(t)\geq 1\right ] \right ). \end{align*}
\begin{align*} {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)} \geq t \right ] & \leq \sum _{v\in V} \prod _{i=1}^k\left (1-{\mathbb{P}}_{\pi }\!\left [N_v^{(i)}(t)\geq 1\right ]\right )\leq \sum _{v\in V}\exp\!\left (-k{\mathbb{P}}_{\pi }\!\left [N_v(t)\geq 1\right ] \right ). \end{align*}
For Item (ii), since
![]() $N_v(t)$
is a non-negative integer, we have
$N_v(t)$
is a non-negative integer, we have
For the two inequalities first observe that
![]() ${\mathbb{E}}_{\pi } [N_v(t)]=(t+1)\pi (v)$
. Now, conditional on a walk first hitting
${\mathbb{E}}_{\pi } [N_v(t)]=(t+1)\pi (v)$
. Now, conditional on a walk first hitting
![]() $v$
at time
$v$
at time
![]() $s$
we have
$s$
we have
![]() $N_v(t)= \sum _{i=0}^{t-s}P_{v,v}^{t}$
. The first inequality in Item (ii) then follows since
$N_v(t)= \sum _{i=0}^{t-s}P_{v,v}^{t}$
. The first inequality in Item (ii) then follows since
![]() ${\mathbb{E}}_{\pi } [N_v(t)\mid N_v(t)\geq 1]\leq \sum _{i=0}^t P_{v,v}^{i}$
. For the last inequality in Item (ii), observe that, by reversibility, for any
${\mathbb{E}}_{\pi } [N_v(t)\mid N_v(t)\geq 1]\leq \sum _{i=0}^t P_{v,v}^{i}$
. For the last inequality in Item (ii), observe that, by reversibility, for any
![]() $t\geq 1$
$t\geq 1$
 \begin{align*} {\mathbb{P}}_{\pi }\!\left [N_v\left (\left \lceil \tfrac{t-1}{2}\right \rceil \right )\geq 1,\; N_v( t) \geq 1\right ] &= \sum _{v_0v_1\cdots v_t : v\in \bigcup _{i=0}^{\lceil \frac{t-1}{2}\rceil }\{v_i\} } \pi (v_0)P_{v_0,v_1}\cdots P_{v_{t-1},v_t} \\[5pt] &= \sum _{v_0v_1\cdots v_t : v\in \bigcup _{i=0}^{\lceil \frac{t-1}{2}\rceil }\{v_i\} } \pi (v_t)P_{v_t,v_{t-1}}\cdots P_{v_{1},v_0}\\[5pt] &= {\mathbb{P}}_{\pi }\!\left [N_v(t)- N_v\left (\left \lfloor \tfrac{t+1}{2}\right \rfloor -1\right )\geq 1,\; N_v( t) \geq 1\right ]. \end{align*}
\begin{align*} {\mathbb{P}}_{\pi }\!\left [N_v\left (\left \lceil \tfrac{t-1}{2}\right \rceil \right )\geq 1,\; N_v( t) \geq 1\right ] &= \sum _{v_0v_1\cdots v_t : v\in \bigcup _{i=0}^{\lceil \frac{t-1}{2}\rceil }\{v_i\} } \pi (v_0)P_{v_0,v_1}\cdots P_{v_{t-1},v_t} \\[5pt] &= \sum _{v_0v_1\cdots v_t : v\in \bigcup _{i=0}^{\lceil \frac{t-1}{2}\rceil }\{v_i\} } \pi (v_t)P_{v_t,v_{t-1}}\cdots P_{v_{1},v_0}\\[5pt] &= {\mathbb{P}}_{\pi }\!\left [N_v(t)- N_v\left (\left \lfloor \tfrac{t+1}{2}\right \rfloor -1\right )\geq 1,\; N_v( t) \geq 1\right ]. \end{align*}
Since
![]() $\{N_v( t) \geq 1 \}=\{N_v\left (\left \lceil \tfrac{t-1}{2}\right \rceil \right )\geq 1 \}\cup \{N_v(t)- N_v\left (\left \lfloor \tfrac{t+1}{2}\right \rfloor -1\right )\geq 1\}$
we have
$\{N_v( t) \geq 1 \}=\{N_v\left (\left \lceil \tfrac{t-1}{2}\right \rceil \right )\geq 1 \}\cup \{N_v(t)- N_v\left (\left \lfloor \tfrac{t+1}{2}\right \rfloor -1\right )\geq 1\}$
we have
Thus
![]() ${\mathbb{E}}_{\pi } \!\left [N_v(t) \mid N_v(t)\geq 1\right ] \geq (1/2)\cdot \sum _{i=0}^{\lceil \frac{t-1}{2}\rceil }P_{v,v}^{i}$
as claimed.
${\mathbb{E}}_{\pi } \!\left [N_v(t) \mid N_v(t)\geq 1\right ] \geq (1/2)\cdot \sum _{i=0}^{\lceil \frac{t-1}{2}\rceil }P_{v,v}^{i}$
as claimed.
Finally, for Item (iii), the proof of [Reference Oliveira, Peres, Mishna and Munro51, Lemma 1] shows that
 \begin{equation*}\sum _{i=0}^t P_{u,u}^{i} - (t+1)\pi (u)\leq \frac {e}{e-1}\left (\sum _{i=0}^{\lceil t_{\mathsf {rel}} \rceil -1}P_{u,u}^{i} -\lceil t_{\mathsf {rel}} \rceil \pi (u)\right ),\end{equation*}
\begin{equation*}\sum _{i=0}^t P_{u,u}^{i} - (t+1)\pi (u)\leq \frac {e}{e-1}\left (\sum _{i=0}^{\lceil t_{\mathsf {rel}} \rceil -1}P_{u,u}^{i} -\lceil t_{\mathsf {rel}} \rceil \pi (u)\right ),\end{equation*}
rearranging gives the result.
Recall
![]() $a\wedge b$
denotes
$a\wedge b$
denotes
![]() $\min ( a, b )$
. We shall use the following result of Oliveira and Peres [Reference Oliveira, Peres, Mishna and Munro51, Theorem 2] for lazy walks: for any
$\min ( a, b )$
. We shall use the following result of Oliveira and Peres [Reference Oliveira, Peres, Mishna and Munro51, Theorem 2] for lazy walks: for any
![]() $v\in V$
and
$v\in V$
and
![]() $t\geq 0$
we have
$t\geq 0$
we have
Note that we prove Theorem 3.1 for lazy walks however this also applies to non-lazy walks as the cover time of a lazy walk stochastically dominates that of a non-lazy walk.
Proof of Theorem
3.1. Recall that we aim to prove
![]() $t_{\mathsf{cov}}^{(k)}(\pi ) = \mathcal{O} \big ( \big (\frac{m}{kd_{\mathsf{min}}}\big )^2\log ^2 n \big )$
. To begin observe that if
$t_{\mathsf{cov}}^{(k)}(\pi ) = \mathcal{O} \big ( \big (\frac{m}{kd_{\mathsf{min}}}\big )^2\log ^2 n \big )$
. To begin observe that if
![]() $k\geq 10 (m/d_{\mathsf{min}} )\log n$
then the probability any vertex
$k\geq 10 (m/d_{\mathsf{min}} )\log n$
then the probability any vertex
![]() $u$
is unoccupied at time
$u$
is unoccupied at time
![]() $0$
is
$0$
is
![]() $(1-\pi (u))^k\leq e^{-\pi (u)k}\leq e^{-d_{\mathsf{min}} k/(2m)}$
. For any graph
$(1-\pi (u))^k\leq e^{-\pi (u)k}\leq e^{-d_{\mathsf{min}} k/(2m)}$
. For any graph
![]() $t_{\mathsf{cov}} \leq 16mn/d_{\mathsf{min}} \leq 16n^3$
by [Reference Kahn, Linial, Nisan and Saks34, Theorem 2], thus we have
$t_{\mathsf{cov}} \leq 16mn/d_{\mathsf{min}} \leq 16n^3$
by [Reference Kahn, Linial, Nisan and Saks34, Theorem 2], thus we have
It follows that we can assume
![]() $k\leq 10 (m/d_{\mathsf{min}} )\log n$
for the remainder of the proof.
$k\leq 10 (m/d_{\mathsf{min}} )\log n$
for the remainder of the proof.
We will apply Lemma 3.10 to bound
![]() ${\mathbb{P}}_{\pi ^k}\left[\tau _{\mathsf{cov}}^{(k)} \geq t \right]$
for
${\mathbb{P}}_{\pi ^k}\left[\tau _{\mathsf{cov}}^{(k)} \geq t \right]$
for
![]() $t\geq 1$
. To begin, by (2) we have
$t\geq 1$
. To begin, by (2) we have
 \begin{align*} \sum _{i=0}^{t} P_{u,u}^{i} &\leq \frac{10d(u)}{d_{\mathsf{min}}}\sum _{i=0}^{t} \frac{1}{\sqrt{i+1}} + (t+1) \pi (u) \leq \frac{10 d(u)}{d_{\mathsf{min}}}\left (\int _{1}^{t} \frac{1}{\sqrt{x}}\, \textrm{d}x +1\right ) + (t+1)\pi (u). \end{align*}
\begin{align*} \sum _{i=0}^{t} P_{u,u}^{i} &\leq \frac{10d(u)}{d_{\mathsf{min}}}\sum _{i=0}^{t} \frac{1}{\sqrt{i+1}} + (t+1) \pi (u) \leq \frac{10 d(u)}{d_{\mathsf{min}}}\left (\int _{1}^{t} \frac{1}{\sqrt{x}}\, \textrm{d}x +1\right ) + (t+1)\pi (u). \end{align*}
Now, since
![]() $d_{\mathsf{min}}\leq d(u)$
,
$d_{\mathsf{min}}\leq d(u)$
,
![]() $\pi (u)\leq 1$
and
$\pi (u)\leq 1$
and
![]() $t\geq 1$
, we have
$t\geq 1$
, we have
 \begin{align*} \sum _{i=0}^{t} P_{u,u}^{i} &\leq \frac{10d(u)}{d_{\mathsf{min}}}\left (\left [2\sqrt{t} - 2\sqrt{1} \right ] + 1 \right )+ t\pi (u) +1 \leq \frac{20d(u)}{d_{\mathsf{min}}}\sqrt{ t} +t\pi (u). \end{align*}
\begin{align*} \sum _{i=0}^{t} P_{u,u}^{i} &\leq \frac{10d(u)}{d_{\mathsf{min}}}\left (\left [2\sqrt{t} - 2\sqrt{1} \right ] + 1 \right )+ t\pi (u) +1 \leq \frac{20d(u)}{d_{\mathsf{min}}}\sqrt{ t} +t\pi (u). \end{align*}
Thus, by Lemma 3.10 (ii) and dividing each term by a factor of
![]() $\pi (u)=d(u)/2m$
we have
$\pi (u)=d(u)/2m$
we have
We now define
![]() $t^* =\left (\frac{300m\log n}{kd_{\mathsf{min}}}\right )^2$
. Firstly if
$t^* =\left (\frac{300m\log n}{kd_{\mathsf{min}}}\right )^2$
. Firstly if
![]() $k\geq 10\log n$
, then for any
$k\geq 10\log n$
, then for any
![]() $t\geq t^*$
we have
$t\geq t^*$
we have
 \begin{equation*}k{\mathbb{P}}_{\pi }\!\left [N_v(t)\geq 1 \right ]\geq \frac {k\left (\frac {300m\log n}{kd_{\mathsf {min}}}\right )^2}{(40m/d_{\mathsf {min}})\cdot \frac {300m\log n}{kd_{\mathsf {min}}} + \left (\frac {300m\log n}{kd_{\mathsf {min}}}\right )^2} \geq \frac {300\log n }{40+300/10}\gt 4\log n. \end{equation*}
\begin{equation*}k{\mathbb{P}}_{\pi }\!\left [N_v(t)\geq 1 \right ]\geq \frac {k\left (\frac {300m\log n}{kd_{\mathsf {min}}}\right )^2}{(40m/d_{\mathsf {min}})\cdot \frac {300m\log n}{kd_{\mathsf {min}}} + \left (\frac {300m\log n}{kd_{\mathsf {min}}}\right )^2} \geq \frac {300\log n }{40+300/10}\gt 4\log n. \end{equation*}
Now, since
![]() $t_{\mathsf{cov}}\leq 16n^3$
, Lemma 3.10(i) gives
$t_{\mathsf{cov}}\leq 16n^3$
, Lemma 3.10(i) gives
![]() ${\mathbb{E}}_{\pi ^k} \left [\tau _{\mathsf{cov}}^{(k)}\right ]\leq t^* +o\!\left (n^{-3}\right )\cdot 16n^3 = \mathcal{O}\big (\big (\frac{m}{kd_{\mathsf{min}}}\big )^2\log ^2 n\big )$
.
${\mathbb{E}}_{\pi ^k} \left [\tau _{\mathsf{cov}}^{(k)}\right ]\leq t^* +o\!\left (n^{-3}\right )\cdot 16n^3 = \mathcal{O}\big (\big (\frac{m}{kd_{\mathsf{min}}}\big )^2\log ^2 n\big )$
.
Finally, if
![]() $k\leq 10\log n$
then
$k\leq 10\log n$
then
![]() $ t^*\geq (300m/d_{\mathsf{min}})^2/100 =900(m/d_{\mathsf{min}})^2$
. However,
$ t^*\geq (300m/d_{\mathsf{min}})^2/100 =900(m/d_{\mathsf{min}})^2$
. However,
![]() $t_{\mathsf{cov}} \leq 16mn/d_{\mathsf{min}} \leq 32m^2/d_{\mathsf{min}}^2$
by [Reference Kahn, Linial, Nisan and Saks34, Theorem 2]. Thus,
$t_{\mathsf{cov}} \leq 16mn/d_{\mathsf{min}} \leq 32m^2/d_{\mathsf{min}}^2$
by [Reference Kahn, Linial, Nisan and Saks34, Theorem 2]. Thus,
![]() ${\mathbb{E}}_{\pi ^k} \!\left[t_{\mathsf{cov}}^{(k)}\right]\leq t^*$
holds as claimed.
${\mathbb{E}}_{\pi ^k} \!\left[t_{\mathsf{cov}}^{(k)}\right]\leq t^*$
holds as claimed.
Proof of Theorem
3.2. We consider first the case
![]() $k \lt 8\log _2 n$
. To begin, for any pair
$k \lt 8\log _2 n$
. To begin, for any pair
![]() $u,v$
it holds that
$u,v$
it holds that
![]() ${\mathbb{E}}_{u} [\tau _{v}] \leq 2\max _{w\in V}{\mathbb{E}}_{\pi } [\tau _{w}]$
by [Reference Levin, Peres and Wilmer42, Lemma 10.2]. Thus by Markov’s inequality
${\mathbb{E}}_{u} [\tau _{v}] \leq 2\max _{w\in V}{\mathbb{E}}_{\pi } [\tau _{w}]$
by [Reference Levin, Peres and Wilmer42, Lemma 10.2]. Thus by Markov’s inequality
for any
![]() $v\in V$
. Then, the Markov property yields
$v\in V$
. Then, the Markov property yields
Thus, by independence of the
![]() $k$
walks
$k$
walks
and finally by the union bound,
Therefore, since the cover time of a single walk satisfies
![]() $t_{\mathsf{cov}} =\mathcal{O}(n^3 )$
, we have
$t_{\mathsf{cov}} =\mathcal{O}(n^3 )$
, we have
We now cover the case
![]() $ 8\log _2 n\leq k \leq 100\max _{v\in V}{\mathbb{E}}_{\pi } [\tau _v] \cdot \log n$
, where we apply Items (i) & (ii) of Lemma 3.10 to bound
$ 8\log _2 n\leq k \leq 100\max _{v\in V}{\mathbb{E}}_{\pi } [\tau _v] \cdot \log n$
, where we apply Items (i) & (ii) of Lemma 3.10 to bound
![]() ${\mathbb{P}}_{\pi ^k}\!\left[\tau _{\mathsf{cov}}^{(k)} \geq t \right]$
. Observe that
${\mathbb{P}}_{\pi ^k}\!\left[\tau _{\mathsf{cov}}^{(k)} \geq t \right]$
. Observe that
 \begin{align*} \sum _{i=0}^{t} P_{v,v}^i = \sum _{i=0}^{t} (P_{v,v}^i-\pi (v)) + (t+1)\pi (v). \end{align*}
\begin{align*} \sum _{i=0}^{t} P_{v,v}^i = \sum _{i=0}^{t} (P_{v,v}^i-\pi (v)) + (t+1)\pi (v). \end{align*}
Since the walk is lazy
![]() $(P_{v,v}^i-\pi (v))$
is non-negative and non-increasing in
$(P_{v,v}^i-\pi (v))$
is non-negative and non-increasing in
![]() $i$
[Reference Levin, Peres and Wilmer42, Exercise 12.5]. Thus
$i$
[Reference Levin, Peres and Wilmer42, Exercise 12.5]. Thus
 \begin{align*} \sum _{i=0}^{t} P_{v,v}^i \leq \sum _{i=0}^{\infty } (P_{v,v}^i-\pi (v)) + (t+1)\pi (v) = \pi (v){\mathbb{E}}_{\pi } \!\left [\tau _v\right ]+ (t+1)\pi (v), \end{align*}
\begin{align*} \sum _{i=0}^{t} P_{v,v}^i \leq \sum _{i=0}^{\infty } (P_{v,v}^i-\pi (v)) + (t+1)\pi (v) = \pi (v){\mathbb{E}}_{\pi } \!\left [\tau _v\right ]+ (t+1)\pi (v), \end{align*}
as
![]() $\pi (v){\mathbb{E}}_{\pi } [\tau _v]=\sum _{i=0}^{\infty } (P_{v,v}^i-\pi (v))$
by [Reference Aldous and Fill2, Lemma 2.11]. Now, by Lemma 3.10 (ii) we have
$\pi (v){\mathbb{E}}_{\pi } [\tau _v]=\sum _{i=0}^{\infty } (P_{v,v}^i-\pi (v))$
by [Reference Aldous and Fill2, Lemma 2.11]. Now, by Lemma 3.10 (ii) we have
Choosing
![]() $t = 8\left \lceil \frac{\log n}{k}\max _{v\in V}{\mathbb{E}}_{\pi } \!\left [\tau _v\right ] \right \rceil$
yields
$t = 8\left \lceil \frac{\log n}{k}\max _{v\in V}{\mathbb{E}}_{\pi } \!\left [\tau _v\right ] \right \rceil$
yields
since
![]() $k\geq 8\log n$
. Then an application of Lemma 3.10 (i) gives
$k\geq 8\log n$
. Then an application of Lemma 3.10 (i) gives
Again, as
![]() $t_{\mathsf{cov}} = \mathcal O(n^3)$
, we conclude
$t_{\mathsf{cov}} = \mathcal O(n^3)$
, we conclude
![]() ${\mathbb{E}}_{\pi ^k} \left [t_{\mathsf{cov}}^{(k)}\right ] \leq 8\left \lceil \frac{\log n}{k}\max _{v\in V}{\mathbb{E}}_{\pi } \!\left [\tau _v\right ] \right \rceil +\mathcal O(1)$
.
${\mathbb{E}}_{\pi ^k} \left [t_{\mathsf{cov}}^{(k)}\right ] \leq 8\left \lceil \frac{\log n}{k}\max _{v\in V}{\mathbb{E}}_{\pi } \!\left [\tau _v\right ] \right \rceil +\mathcal O(1)$
.
Finally assume that
![]() $k\geq 100\max _{v\in V}{\mathbb{E}}_{\pi } [\tau _v] \cdot \log n$
. Recall that
$k\geq 100\max _{v\in V}{\mathbb{E}}_{\pi } [\tau _v] \cdot \log n$
. Recall that
![]() $ \max _v{\mathbb{E}}_{\pi } [\tau _v] \geq (1/2) \cdot \max _{x,y}{\mathbb{E}}_{x} [\tau _y]$
by [Reference Aldous and Fill2, Lemma 3.15] and
$ \max _v{\mathbb{E}}_{\pi } [\tau _v] \geq (1/2) \cdot \max _{x,y}{\mathbb{E}}_{x} [\tau _y]$
by [Reference Aldous and Fill2, Lemma 3.15] and
![]() $\max _{x,y}{\mathbb{E}}_{x} [\tau _y] \geq \max _{x,y} m R(x,y)$
by the commute time identity [Reference Levin, Peres and Wilmer42, Proposition 10.6], where
$\max _{x,y}{\mathbb{E}}_{x} [\tau _y] \geq \max _{x,y} m R(x,y)$
by the commute time identity [Reference Levin, Peres and Wilmer42, Proposition 10.6], where
![]() $R(x,y)$
is the effective resistance between
$R(x,y)$
is the effective resistance between
![]() $x$
and
$x$
and
![]() $y$
(see [Reference Levin, Peres and Wilmer42, Section 9.4]). Thus we have
$y$
(see [Reference Levin, Peres and Wilmer42, Section 9.4]). Thus we have
as
![]() $R(x,y)\geq \max \{1/d(x),1/d(y)\}$
by the definition of the effective resistance. The probability that any vertex
$R(x,y)\geq \max \{1/d(x),1/d(y)\}$
by the definition of the effective resistance. The probability that any vertex
![]() $u$
is unoccupied at time
$u$
is unoccupied at time
![]() $0$
is
$0$
is
![]() $(1-\pi (u))^k\leq e^{-\pi (u)k}$
. For any graph
$(1-\pi (u))^k\leq e^{-\pi (u)k}$
. For any graph
![]() $t_{\mathsf{cov}} \leq 16n^3$
by [Reference Kahn, Linial, Nisan and Saks34, Theorem 2] and thus, one can check that by (3), we have
$t_{\mathsf{cov}} \leq 16n^3$
by [Reference Kahn, Linial, Nisan and Saks34, Theorem 2] and thus, one can check that by (3), we have
as claimed.
Proof of Lemma
3.4. The lower bound will follow from the general lower bound we prove later in Theorem 3.6. For the upper bound notice that, by Lemma 3.10 (iii) and our hypothesis that
![]() $\sum _{i=0}^{t} P_{vv}^i =\mathcal{O}(1 + t\pi (v) )$
for any
$\sum _{i=0}^{t} P_{vv}^i =\mathcal{O}(1 + t\pi (v) )$
for any
![]() $t\leq t_{\mathsf{rel}}$
, we have that for any
$t\leq t_{\mathsf{rel}}$
, we have that for any
![]() $T\geq 0$
,
$T\geq 0$
,
 \begin{equation*} \sum _{t=0}^T P_{v,v}^t \leq \frac {e}{e-1}\left (\sum _{i=0}^{\lceil t_{\mathsf {rel}} \rceil -1}P_{v,v}^{i} -\lceil t_{\mathsf {rel}} \rceil \pi (v)\right )+ (T+1)\pi (v)\leq C(1 + T\pi (v)), \end{equation*}
\begin{equation*} \sum _{t=0}^T P_{v,v}^t \leq \frac {e}{e-1}\left (\sum _{i=0}^{\lceil t_{\mathsf {rel}} \rceil -1}P_{v,v}^{i} -\lceil t_{\mathsf {rel}} \rceil \pi (v)\right )+ (T+1)\pi (v)\leq C(1 + T\pi (v)), \end{equation*}
for some constant
![]() $C\lt \infty$
. Now, by Lemma 3.10 (ii) and as
$C\lt \infty$
. Now, by Lemma 3.10 (ii) and as
![]() $\pi _{\mathsf{min}} =\Omega (1/n)$
holds by hypothesis, for any
$\pi _{\mathsf{min}} =\Omega (1/n)$
holds by hypothesis, for any
![]() $v$
and
$v$
and
![]() $T= \mathcal{O}(n )$
there exists a constant
$T= \mathcal{O}(n )$
there exists a constant
![]() $C'\lt \infty$
such that
$C'\lt \infty$
such that
First consider
![]() $k=\omega (\!\log n)$
, and let
$k=\omega (\!\log n)$
, and let
![]() $T= \lceil 4C'(n/k)\log n \rceil =\mathcal{O}(n )$
. Lemma 3.10 (i) and (4) give
$T= \lceil 4C'(n/k)\log n \rceil =\mathcal{O}(n )$
. Lemma 3.10 (i) and (4) give
Otherwise, if
![]() $k = \mathcal{O}(\!\log n )$
, then we consider consecutive periods of length
$k = \mathcal{O}(\!\log n )$
, then we consider consecutive periods of length
![]() $5t_{\mathsf{mix}}= \mathcal{O}(n )$
. For any
$5t_{\mathsf{mix}}= \mathcal{O}(n )$
. For any
![]() $u,v\in V$
, (4) gives
$u,v\in V$
, (4) gives
The probability that a vertex
![]() $v$
is not hit in a period, starting from any vector in
$v$
is not hit in a period, starting from any vector in
![]() $V^k$
is
$V^k$
is
and thus after
![]() $20C'\lceil \frac{n}{k t_{\mathsf{mix}}}\cdot \log n\rceil$
periods the probability
$20C'\lceil \frac{n}{k t_{\mathsf{mix}}}\cdot \log n\rceil$
periods the probability
![]() $v$
has not been hit is at most
$v$
has not been hit is at most
![]() $e^{-5 \log n}= n^{-5}$
. By the union bound, and since worst-case cover time of a single walk on any graph is
$e^{-5 \log n}= n^{-5}$
. By the union bound, and since worst-case cover time of a single walk on any graph is
![]() $\mathcal{O}(n^3 )$
, the cover time is
$\mathcal{O}(n^3 )$
, the cover time is
![]() $\mathcal{O}\!\left (t_{\mathsf{mix}} \cdot \frac{n}{k t_{\mathsf{mix}}}\cdot \log n \right )= \mathcal{O}\!\left (\frac{n}{k}\cdot \log n\right )$
.
$\mathcal{O}\!\left (t_{\mathsf{mix}} \cdot \frac{n}{k t_{\mathsf{mix}}}\cdot \log n \right )= \mathcal{O}\!\left (\frac{n}{k}\cdot \log n\right )$
.
Proof of Lemma
3.5. From Lemma 3.10 (iii) we deduce that
![]() $\sum _{i=0}^{t} P_{v,v}^i = \mathcal{O}(1+ t/n+\log t )$
for any
$\sum _{i=0}^{t} P_{v,v}^i = \mathcal{O}(1+ t/n+\log t )$
for any
![]() $t\leq n(\!\log n)^2$
. Thus we can apply Lemma 3.10 (ii) which, for any
$t\leq n(\!\log n)^2$
. Thus we can apply Lemma 3.10 (ii) which, for any
![]() $2\leq t \leq n(\!\log n)^2$
, gives
$2\leq t \leq n(\!\log n)^2$
, gives
for some fixed constant
![]() $c\gt 0$
. Let
$c\gt 0$
. Let
![]() $t^*=C \frac{n\log n}{k}\log \left (\frac{n\log n}{k}\right )$
and
$t^*=C \frac{n\log n}{k}\log \left (\frac{n\log n}{k}\right )$
and
![]() $C\log n \leq k \leq (n\log n )/3$
for some constant
$C\log n \leq k \leq (n\log n )/3$
for some constant
![]() $1\lt C\;:\!=\;C(c)\lt \infty$
to be determined later then,
$1\lt C\;:\!=\;C(c)\lt \infty$
to be determined later then,
In addition we have
Thus inserting (6) into (5) then applying (7) yields the following for any
![]() $v\in V$
,
$v\in V$
,
 \begin{equation*}k{\mathbb{P}}_{\pi }\!\left [\tau _v\leq t\right ] \geq \frac {c}{2} \cdot \frac {kt^*}{n\log t^*} \geq \frac {c }{2 }\cdot \frac {(Cn\log n)\log \left (\frac {n\log n}{k}\right ) }{(2 + \log C)n\log \left (\frac {n\log n}{k}\right )} = \frac {Cc \log n }{4 + 2\log C } .\end{equation*}
\begin{equation*}k{\mathbb{P}}_{\pi }\!\left [\tau _v\leq t\right ] \geq \frac {c}{2} \cdot \frac {kt^*}{n\log t^*} \geq \frac {c }{2 }\cdot \frac {(Cn\log n)\log \left (\frac {n\log n}{k}\right ) }{(2 + \log C)n\log \left (\frac {n\log n}{k}\right )} = \frac {Cc \log n }{4 + 2\log C } .\end{equation*}
We can assume w.l.o.g. that
![]() $c\lt 1$
and thus taking
$c\lt 1$
and thus taking
![]() $C= 100/c^2$
yields
$C= 100/c^2$
yields
![]() $\frac{Cc }{4 + 2\log C } \gt \frac{100/c}{14 + 4\log\!(1/c)} \gt 5$
. So by independence of the walks we have
$\frac{Cc }{4 + 2\log C } \gt \frac{100/c}{14 + 4\log\!(1/c)} \gt 5$
. So by independence of the walks we have
Thus, by the union bound
![]() ${\mathbb{P}}_{\pi ^k}\!\left[\tau _\mathsf{cov}^{(k)} \gt t^* \right]\leq n^{-4}$
. So, since the worst-case expected cover time by a single walk on any graph is
${\mathbb{P}}_{\pi ^k}\!\left[\tau _\mathsf{cov}^{(k)} \gt t^* \right]\leq n^{-4}$
. So, since the worst-case expected cover time by a single walk on any graph is
![]() $\mathcal{O}(n^3 )$
, we have
$\mathcal{O}(n^3 )$
, we have
![]() $t_{\mathsf{cov}}^{(k)}(\mathcal{T}_n,\pi )= \mathcal{O}(t^* )$
, as claimed.
$t_{\mathsf{cov}}^{(k)}(\mathcal{T}_n,\pi )= \mathcal{O}(t^* )$
, as claimed.
The case
![]() $k\leq (100\log n )/c^2$
remains. For any
$k\leq (100\log n )/c^2$
remains. For any
![]() $k = \mathcal{O}(\!\log n )$
, consider periods of length
$k = \mathcal{O}(\!\log n )$
, consider periods of length
![]() $5t_{\mathsf{mix}}=\mathcal{O}(n )$
. Then by Lemma 3.10 (ii), for any pair of vertices
$5t_{\mathsf{mix}}=\mathcal{O}(n )$
. Then by Lemma 3.10 (ii), for any pair of vertices
![]() $v,w$
and some
$v,w$
and some
![]() $C'\lt \infty$
, we have
$C'\lt \infty$
, we have
Thus the probability
![]() $v\in V$
is not hit in a period, starting from any configuration in
$v\in V$
is not hit in a period, starting from any configuration in
![]() $ V^k$
is
$ V^k$
is
Thus after
![]() $5C'\lceil (n\log ^2 n)/(k t_{\mathsf{mix}})\rceil$
periods the probability
$5C'\lceil (n\log ^2 n)/(k t_{\mathsf{mix}})\rceil$
periods the probability
![]() $v$
has not been hit is at most
$v$
has not been hit is at most
![]() $e^{-5 \log n}= n^{-5}$
, so (similarly) the cover time is
$e^{-5 \log n}= n^{-5}$
, so (similarly) the cover time is
![]() $\mathcal{O}\!\left (t_{\mathsf{mix}} \cdot \frac{n\log ^2 n}{k t_{\mathsf{mix}}}\right )= \mathcal{O}\!\left (\frac{n}{k}\cdot \log ^2 n\right )$
as claimed.
$\mathcal{O}\!\left (t_{\mathsf{mix}} \cdot \frac{n\log ^2 n}{k t_{\mathsf{mix}}}\right )= \mathcal{O}\!\left (\frac{n}{k}\cdot \log ^2 n\right )$
as claimed.
3.4. Proofs of lower bounds
We begin by proving the lower bound obtained by the reset coupling.
Proof of Lemma
3.8. Let
![]() $x = Ck/T$
, and recall that in each step that the random walk on
$x = Ck/T$
, and recall that in each step that the random walk on
![]() $\widehat{G}(x)$
is not at the vertex
$\widehat{G}(x)$
is not at the vertex
![]() $z$
, it moves to
$z$
, it moves to
![]() $z$
with probability
$z$
with probability
![]() $x$
. For
$x$
. For
![]() $i\geq 1$
, we refer to the portion of the walk between the
$i\geq 1$
, we refer to the portion of the walk between the
![]() $i$
th and
$i$
th and
![]() $(i+1)$
th visits to
$(i+1)$
th visits to
![]() $z$
as the
$z$
as the
![]() $i$
th sub-walk. For
$i$
th sub-walk. For
![]() $i\geq 0$
let
$i\geq 0$
let
![]() $X_i\sim \operatorname{Geo}\!(x )$
be i.i.d. geometric random variables with mean
$X_i\sim \operatorname{Geo}\!(x )$
be i.i.d. geometric random variables with mean
![]() $1/x$
, then it follows that the
$1/x$
, then it follows that the
![]() $i$
th sub-walk has length
$i$
th sub-walk has length
![]() $X_i+1$
and takes
$X_i+1$
and takes
![]() $X_i-1$
steps inside
$X_i-1$
steps inside
![]() $G$
(the steps leaving and entering
$G$
(the steps leaving and entering
![]() $z$
are not in
$z$
are not in
![]() $G$
) and it takes at most
$G$
) and it takes at most
![]() $X_0$
steps to first visit
$X_0$
steps to first visit
![]() $z$
.
$z$
.
If we let
![]() $X=\sum _{i=0}^{Ck/3}X_i$
then we see that
$X=\sum _{i=0}^{Ck/3}X_i$
then we see that
![]() $X + Ck/3$
stochastically dominates the time taken for the first
$X + Ck/3$
stochastically dominates the time taken for the first
![]() $Ck/3$
sub-walks to occur within a walk on
$Ck/3$
sub-walks to occur within a walk on
![]() $\widehat{G}(x)$
. Observe that
$\widehat{G}(x)$
. Observe that
![]() ${\mathbb{E}} [X] = T/3$
and so a Chernoff bound for sums of geometric r.v.’s [Reference Janson32, Theorem 2.1] gives
${\mathbb{E}} [X] = T/3$
and so a Chernoff bound for sums of geometric r.v.’s [Reference Janson32, Theorem 2.1] gives
Note that
![]() $2{\mathbb{E}} [X]+ Ck/3 \leq T$
. Thus, if
$2{\mathbb{E}} [X]+ Ck/3 \leq T$
. Thus, if
![]() $\mathcal{E}_1$
is the event that there are at least
$\mathcal{E}_1$
is the event that there are at least
![]() $Ck/3$
sub-walks in a walk of length
$Ck/3$
sub-walks in a walk of length
![]() $T$
, then
$T$
, then
![]() ${\mathbb{P}}\left [\mathcal{E}_1^c\right ]\leq e^{-\frac{Ck}{10}}$
.
${\mathbb{P}}\left [\mathcal{E}_1^c\right ]\leq e^{-\frac{Ck}{10}}$
.
For each
![]() $i\geq 0$
, we have
$i\geq 0$
, we have
![]() ${\mathbb{P}} [X_i\geq 1/(2x)]= (1-x)^{1/(2x)}\geq 1/2$
by Bernoulli’s inequality. Let
${\mathbb{P}} [X_i\geq 1/(2x)]= (1-x)^{1/(2x)}\geq 1/2$
by Bernoulli’s inequality. Let
![]() $\mathcal{E}_2$
be the event that
$\mathcal{E}_2$
be the event that
![]() $\{X_i\geq 1/(2x)\}$
holds for more than
$\{X_i\geq 1/(2x)\}$
holds for more than
![]() $k$
values
$k$
values
![]() $1\leq i\leq Ck/3$
. Recall that
$1\leq i\leq Ck/3$
. Recall that
![]() $C\gt 30$
and, as the
$C\gt 30$
and, as the
![]() $X_i$
’s are independent, a Chernoff bound [Reference Mitzenmacher and Upfal49, Theorem 4.5] gives
$X_i$
’s are independent, a Chernoff bound [Reference Mitzenmacher and Upfal49, Theorem 4.5] gives
 \begin{equation*}{\mathbb{P}}\left [\mathcal {E}_2^c\right ]\leq {\mathbb{P}}\left [\operatorname {Bin}\!\left ( \frac {Ck}{3},\frac {1}{2} \right )\leq k\right ]\leq \exp\!\left (- \frac {1}{2}\cdot \left (1-\frac {6}{C}\right )^2\cdot \frac {Ck}{6} \right ) \leq e^{-\frac {Ck}{20}} .\end{equation*}
\begin{equation*}{\mathbb{P}}\left [\mathcal {E}_2^c\right ]\leq {\mathbb{P}}\left [\operatorname {Bin}\!\left ( \frac {Ck}{3},\frac {1}{2} \right )\leq k\right ]\leq \exp\!\left (- \frac {1}{2}\cdot \left (1-\frac {6}{C}\right )^2\cdot \frac {Ck}{6} \right ) \leq e^{-\frac {Ck}{20}} .\end{equation*}
Observe that conditional on
![]() $\mathcal{E}_1\cap \mathcal{E}_2$
there are at least
$\mathcal{E}_1\cap \mathcal{E}_2$
there are at least
![]() $k$
sub-walks which take at least
$k$
sub-walks which take at least
![]() $s$
many steps within
$s$
many steps within
![]() $G$
where
$G$
where
![]() $s= \frac{1}{2x} -1 = \frac{T}{2Ck}-1\geq \frac{T}{10Ck}$
, since
$s= \frac{1}{2x} -1 = \frac{T}{2Ck}-1\geq \frac{T}{10Ck}$
, since
![]() $T\geq 5Ck$
. Recall that at each visit to
$T\geq 5Ck$
. Recall that at each visit to
![]() $z$
the walk on
$z$
the walk on
![]() $\widehat{G}(x)$
moves to a vertex
$\widehat{G}(x)$
moves to a vertex
![]() $v\in V(G)$
proportional to
$v\in V(G)$
proportional to
![]() $\pi (v)$
. It follows that, conditional on
$\pi (v)$
. It follows that, conditional on
![]() $\mathcal{E}_1\cap \mathcal{E}_2$
, we can couple
$\mathcal{E}_1\cap \mathcal{E}_2$
, we can couple
![]() $k$
stationary random walks of length
$k$
stationary random walks of length
![]() $s$
on
$s$
on
![]() $G$
to a single random walk of length
$G$
to a single random walk of length
![]() $T$
on
$T$
on
![]() $\widehat{G}$
such that if the latter walk has not covered
$\widehat{G}$
such that if the latter walk has not covered
![]() $\widehat{G}$
then the former walks have not covered
$\widehat{G}$
then the former walks have not covered
![]() $G$
. Thus
$G$
. Thus
and the result follows since
![]() $ {\mathbb{P}}\left [ \mathcal{E}_1^c\cup \mathcal{E}_2^c\right ] \leq e^{-\frac{Ck}{10}} + e^{-\frac{Ck}{20}}\lt e^{-\frac{Ck}{50}}$
.
$ {\mathbb{P}}\left [ \mathcal{E}_1^c\cup \mathcal{E}_2^c\right ] \leq e^{-\frac{Ck}{10}} + e^{-\frac{Ck}{20}}\lt e^{-\frac{Ck}{50}}$
.
We shall prove the general lower bound with this coupling, however, we must first state a technical lemma.
Lemma 3.11.
For any reversible Markov chain and
![]() $0\lt b\lt 1$
we have
$0\lt b\lt 1$
we have
![]() $ t_{\mathsf{cov}}\leq 2t_{\mathsf{cov}}(\pi )$
and
$ t_{\mathsf{cov}}\leq 2t_{\mathsf{cov}}(\pi )$
and
![]() ${\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\gt b\cdot t_{\mathsf{cov}}(\pi ) \right ] \gt \frac{1-b}{2}$
.
${\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\gt b\cdot t_{\mathsf{cov}}(\pi ) \right ] \gt \frac{1-b}{2}$
.
Proof of Lemma
3.11. We first show
![]() $t_{\mathsf{cov}}\leq 2t_{\mathsf{cov}}(\pi )$
. The Random Target Lemma [Reference Levin, Peres and Wilmer42, Lemma 10.1] states that
$t_{\mathsf{cov}}\leq 2t_{\mathsf{cov}}(\pi )$
. The Random Target Lemma [Reference Levin, Peres and Wilmer42, Lemma 10.1] states that
![]() ${\mathbb{E}}_{x} [\tau _\pi ]=\sum _{v\in V}{\mathbb{E}}_{x} [\tau _v]\pi (v)$
does not depend on
${\mathbb{E}}_{x} [\tau _\pi ]=\sum _{v\in V}{\mathbb{E}}_{x} [\tau _v]\pi (v)$
does not depend on
![]() $x\in V$
. Thus, for any
$x\in V$
. Thus, for any
![]() $u\in V$
,
$u\in V$
,
Then, since choosing a vertex
![]() $v$
independently from
$v$
independently from
![]() $\pi$
and waiting for the random walk to hit
$\pi$
and waiting for the random walk to hit
![]() $v$
is a strong stationary time for the random walk, we have
$v$
is a strong stationary time for the random walk, we have
Observe that, by the Markov Property, for any
![]() $0\lt b\lt 1$
we have
$0\lt b\lt 1$
we have
 \begin{align*} t_{\mathsf{cov}}(\pi ) &\leq b t_{\mathsf{cov}}(\pi )\cdot {\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\leq bt_{\mathsf{cov}}(\pi ) \right ]+(b t_{\mathsf{cov}}(\pi ) + t_{\mathsf{cov}})\cdot {\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\gt bt_{\mathsf{cov}}(\pi ) \right ]\\[5pt] &= b t_{\mathsf{cov}}(\pi ) + t_{\mathsf{cov}}\cdot {\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\gt b t_{\mathsf{cov}}(\pi ) \right ]\\[5pt] &\leq b t_{\mathsf{cov}}(\pi ) + 2t_{\mathsf{cov}}(\pi )\cdot {\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\gt b t_{\mathsf{cov}}(\pi ) \right ], \end{align*}
\begin{align*} t_{\mathsf{cov}}(\pi ) &\leq b t_{\mathsf{cov}}(\pi )\cdot {\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\leq bt_{\mathsf{cov}}(\pi ) \right ]+(b t_{\mathsf{cov}}(\pi ) + t_{\mathsf{cov}})\cdot {\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\gt bt_{\mathsf{cov}}(\pi ) \right ]\\[5pt] &= b t_{\mathsf{cov}}(\pi ) + t_{\mathsf{cov}}\cdot {\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\gt b t_{\mathsf{cov}}(\pi ) \right ]\\[5pt] &\leq b t_{\mathsf{cov}}(\pi ) + 2t_{\mathsf{cov}}(\pi )\cdot {\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\gt b t_{\mathsf{cov}}(\pi ) \right ], \end{align*}
as
![]() $t_{\mathsf{cov}}\leq 2t_{\mathsf{cov}}(\pi )$
. Rearranging gives
$t_{\mathsf{cov}}\leq 2t_{\mathsf{cov}}(\pi )$
. Rearranging gives
![]() ${\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\gt b\cdot t_{\mathsf{cov}}(\pi ) \right ] \geq \frac{1-b}{2}$
.
${\mathbb{P}}_{\pi }\!\left [\tau _{\mathsf{cov}}\gt b\cdot t_{\mathsf{cov}}(\pi ) \right ] \geq \frac{1-b}{2}$
.
Before proving Theorem 3.6 we must recall a result by Aldous [Reference Aldous3].
Theorem 3.12. ([Reference Aldous3, Theorem 1]). Let
![]() $(X_t)_{t\geq 0}$
be a stationary Markov chain on a state space
$(X_t)_{t\geq 0}$
be a stationary Markov chain on a state space
![]() $I$
with irreducible transition matrix
$I$
with irreducible transition matrix
![]() $P_{i,j}$
and stationary distribution
$P_{i,j}$
and stationary distribution
![]() $\pi$
. Let
$\pi$
. Let
![]() $\tau _{\mathsf{cov}}$
be the cover time and define
$\tau _{\mathsf{cov}}$
be the cover time and define
![]() $t^{*}$
to be the solution of
$t^{*}$
to be the solution of
Let
![]() $0 \lt \theta \lt 1$
and suppose the following hypotheses are satisfied:
$0 \lt \theta \lt 1$
and suppose the following hypotheses are satisfied:
-
(a)
 $P_{i,i} = 0$
for all
$P_{i,i} = 0$
for all
 $i\in I$
.
$i\in I$
. -
(b)
 $\sum _{j\in J}\exp\!(\! -t^{*} \cdot \pi (j) )\geq \theta$
where
$\sum _{j\in J}\exp\!(\! -t^{*} \cdot \pi (j) )\geq \theta$
where
 $J\subseteq I$
is the set of states
$J\subseteq I$
is the set of states
 $j$
such that
$j$
such that
 $\max _{i\in I }P_{i,j}\leq 1 - \theta$
.
$\max _{i\in I }P_{i,j}\leq 1 - \theta$
. -
(c) The chain is reversible; that is
 $\pi (i)P_{i,j} = \pi (j) P_{j,i}$
for all
$\pi (i)P_{i,j} = \pi (j) P_{j,i}$
for all
 $i, j\in I$
.
$i, j\in I$
.
Then
![]() ${\mathbb{E}} [\tau _{\mathsf{cov}}]\geq c_0 t^*$
, where
${\mathbb{E}} [\tau _{\mathsf{cov}}]\geq c_0 t^*$
, where
![]() $c_0 \gt \theta$
depends only on
$c_0 \gt \theta$
depends only on
![]() $\theta$
.
$\theta$
.
We now have all the pieces we need to prove Theorem 3.6.
Proof of Theorem
3.6. We wish to apply Theorem 3.12 to the geometric reset graph
![]() $\widehat{G}(x)$
for some suitable
$\widehat{G}(x)$
for some suitable
![]() $x\;:\!=\;x(n,k)$
. The following claim is based on [Reference Aldous3, Proposition 2].
$x\;:\!=\;x(n,k)$
. The following claim is based on [Reference Aldous3, Proposition 2].
Claim 3.13.
For
![]() $n\geq 3$
and
$n\geq 3$
and
![]() $0\lt x \leq 1/2$
the walk on
$0\lt x \leq 1/2$
the walk on
![]() $\widehat{G}(x)$
satisfies Theorem 3.12 with
$\widehat{G}(x)$
satisfies Theorem 3.12 with
![]() $\theta =1/2$
.
$\theta =1/2$
.
Proof of Claim. Let
![]() $\pi$
and
$\pi$
and
![]() $\widehat{\pi }$
denote the stationary distributions of
$\widehat{\pi }$
denote the stationary distributions of
![]() $G$
and
$G$
and
![]() $\widehat{G}$
, respectively. Note that for any
$\widehat{G}$
, respectively. Note that for any
![]() $x\lt 1$
the walk on the weighted graph
$x\lt 1$
the walk on the weighted graph
![]() $\widehat{G}(x)$
satisfies
$\widehat{G}(x)$
satisfies
![]() $P_{i,i}=0$
and is reversible. These are items (a) and (c) from Theorem 3.12 and we now prove item (b) also holds for
$P_{i,i}=0$
and is reversible. These are items (a) and (c) from Theorem 3.12 and we now prove item (b) also holds for
![]() $\theta =1/2$
.
$\theta =1/2$
.
Partition
![]() $V(\widehat{G})= V(G)\cup \{z\}$
into sets
$V(\widehat{G})= V(G)\cup \{z\}$
into sets
![]() $I_1$
,
$I_1$
,
![]() $I_2$
,
$I_2$
,
![]() $I_3$
as follows. Let
$I_3$
as follows. Let
![]() $I_1$
be the set of leaves of
$I_1$
be the set of leaves of
![]() $G$
, that is vertices of degree
$G$
, that is vertices of degree
![]() $1$
in
$1$
in
![]() $G$
(and degree
$G$
(and degree
![]() $2$
in
$2$
in
![]() $\widehat{G}$
as all vertices are connected to
$\widehat{G}$
as all vertices are connected to
![]() $z$
). Let
$z$
). Let
![]() $I_2$
be the set of vertices of
$I_2$
be the set of vertices of
![]() $V(G)$
which are adjacent to at least one leaf of
$V(G)$
which are adjacent to at least one leaf of
![]() $G$
. Let
$G$
. Let
![]() $I_3$
be the remaining vertices (in particular
$I_3$
be the remaining vertices (in particular
![]() $z \in I_3$
). Let
$z \in I_3$
). Let
![]() $J = I_1 \cup I_3$
and fix
$J = I_1 \cup I_3$
and fix
![]() $j \in J$
. For the case
$j \in J$
. For the case
![]() $j=z$
, by the definition of
$j=z$
, by the definition of
![]() $\widehat{G}$
and by hypothesis, we have
$\widehat{G}$
and by hypothesis, we have
![]() $P_{v,z} =x\leq 1/2$
for any
$P_{v,z} =x\leq 1/2$
for any
![]() $v\in V$
. Otherwise, if
$v\in V$
. Otherwise, if
![]() $i$
is a neighbour of
$i$
is a neighbour of
![]() $j\neq z$
then
$j\neq z$
then
![]() $i$
cannot be a leaf, so
$i$
cannot be a leaf, so
![]() $P_{i,j} = \frac{1-x}{d(i)(1-x)+xd(i)} = \frac{1-x}{d(i)} \leq 1/2$
. Thus it suffices to verify
$P_{i,j} = \frac{1-x}{d(i)(1-x)+xd(i)} = \frac{1-x}{d(i)} \leq 1/2$
. Thus it suffices to verify
Consider an edge
![]() $ik\in E(\widehat{G})$
where
$ik\in E(\widehat{G})$
where
![]() $i\in I_1$
, then we must have
$i\in I_1$
, then we must have
![]() $k\in I_2$
. Since
$k\in I_2$
. Since
![]() $\widehat{\pi }(i)\lt \widehat{\pi }(k)$
we have
$\widehat{\pi }(i)\lt \widehat{\pi }(k)$
we have
![]() $\exp\!(\! -t^{*} \cdot \pi (i) )\geq \exp\!(\! -t^{*} \cdot \pi (k) )$
and also
$\exp\!(\! -t^{*} \cdot \pi (i) )\geq \exp\!(\! -t^{*} \cdot \pi (k) )$
and also
![]() $|I_1|\geq |I_2|$
. Thus, summing over all leaves
$|I_1|\geq |I_2|$
. Thus, summing over all leaves
![]() $i$
gives
$i$
gives
However by the definition of
![]() $t^*$
, the sum over all
$t^*$
, the sum over all
![]() $i\in I$
is equal to
$i\in I$
is equal to
![]() $1$
, thus so (9) implies that the sum over
$1$
, thus so (9) implies that the sum over
![]() $I_2$
is at most
$I_2$
is at most
![]() $1/2$
, and so (8) follows.
$1/2$
, and so (8) follows.
Now since
![]() $t^*\geq n\log n$
by [Reference Aldous3, (1.2)], it follows from Claim 3.13. and Theorem 3.12 that there exists some universal constant
$t^*\geq n\log n$
by [Reference Aldous3, (1.2)], it follows from Claim 3.13. and Theorem 3.12 that there exists some universal constant
![]() $0\lt c\lt \infty$
such that for any
$0\lt c\lt \infty$
such that for any
![]() $0\lt x\leq 1/2$
we have
$0\lt x\leq 1/2$
we have
Thus by Lemma 3.11 we have
![]() ${\mathbb{P}}_{\widehat{\pi },\widehat{G}(x)}\!\left [\tau _{\mathsf{cov}} \gt \frac{c}{2}\cdot n\log n\right ] \geq \frac{1}{4}$
. We seek to apply Lemma 3.8 with
${\mathbb{P}}_{\widehat{\pi },\widehat{G}(x)}\!\left [\tau _{\mathsf{cov}} \gt \frac{c}{2}\cdot n\log n\right ] \geq \frac{1}{4}$
. We seek to apply Lemma 3.8 with
![]() $C=100$
and
$C=100$
and
![]() $T= \frac{c}{2}\cdot n\log n$
. Firstly, we see that the condition
$T= \frac{c}{2}\cdot n\log n$
. Firstly, we see that the condition
![]() $T\geq 5kC$
forces the restriction
$T\geq 5kC$
forces the restriction
![]() $k\leq c'\cdot n \log n$
where
$k\leq c'\cdot n \log n$
where
![]() $c' = \frac{c}{2\cdot 5\cdot C}= \frac{c}{1000}$
for
$c' = \frac{c}{2\cdot 5\cdot C}= \frac{c}{1000}$
for
![]() $0\lt c\lt \infty$
universal. Secondly the condition
$0\lt c\lt \infty$
universal. Secondly the condition
![]() $1/2\geq x = Ck/T$
forces the condition
$1/2\geq x = Ck/T$
forces the condition
![]() $k\leq c''n\log n$
where
$k\leq c''n\log n$
where
![]() $c'' = \frac{c}{2\cdot C}\geq c'$
.
$c'' = \frac{c}{2\cdot C}\geq c'$
.
Thus, provided
![]() $1\leq k\leq c'\cdot n \log n$
holds, all other assumptions are satisfied and we have
$1\leq k\leq c'\cdot n \log n$
holds, all other assumptions are satisfied and we have
by Lemma 3.8. The result follows by taking the constant in the statement to be
![]() $c/2000\leq c'$
, since
$c/2000\leq c'$
, since
![]() $c\gt 0$
is universal.
$c\gt 0$
is universal.
Proof of Lemma
3.9. Let
![]() $X_v= \textbf{1}(\tau _v \gt t)$
be the indicator that
$X_v= \textbf{1}(\tau _v \gt t)$
be the indicator that
![]() $v\in V$
has not been visited up-to time
$v\in V$
has not been visited up-to time
![]() $t$
and
$t$
and
![]() $X = \sum _{v\in S} X_v$
. Let
$X = \sum _{v\in S} X_v$
. Let
![]() $p_v = {\mathbb{P}}_{\pi }[\tau _v\leq t ]$
,
$p_v = {\mathbb{P}}_{\pi }[\tau _v\leq t ]$
,
![]() $p=\max _{v\in S}p_v$
, and observe that
$p=\max _{v\in S}p_v$
, and observe that
![]() ${\mathbb{E}}_{\pi ^k} [X_v] = (1-p_v)^k$
. Thus, we have
${\mathbb{E}}_{\pi ^k} [X_v] = (1-p_v)^k$
. Thus, we have
where the first inequality is by (1) since
![]() $0\leq p\leq 1$
and the last is by the assumption
$0\leq p\leq 1$
and the last is by the assumption
![]() $p^2k \leq 2p^2k \lt 1$
. Let
$p^2k \leq 2p^2k \lt 1$
. Let
![]() $R(t)$
be the number of vertices in
$R(t)$
be the number of vertices in
![]() $S$
that are visited by a single
$S$
that are visited by a single
![]() $t$
-step random walk. Observe that
$t$
-step random walk. Observe that
![]() ${\mathbb{E}}_{\pi } [R(t)] = \sum _{v \in S} p_v$
. Let
${\mathbb{E}}_{\pi } [R(t)] = \sum _{v \in S} p_v$
. Let
![]() $r(v,w) = {\mathbb{P}}_{\pi }[\tau _v\leq t,\tau _w\leq t ]$
, then for any
$r(v,w) = {\mathbb{P}}_{\pi }[\tau _v\leq t,\tau _w\leq t ]$
, then for any
![]() $v,w\in V$
,
$v,w\in V$
,
Recall the identity
![]() $a^k-b^k= (a-b)\sum _{i=0}^{k-1}a^{k-1-i}b^i$
for
$a^k-b^k= (a-b)\sum _{i=0}^{k-1}a^{k-1-i}b^i$
for
![]() $k\geq 2$
. Thus,
$k\geq 2$
. Thus,
 \begin{align*} {\mathbb{E}}_{\pi ^k}[X^2] &= \sum _{v\in S} \sum _{w\in S} (1-p_v-p_w+r(v,w))^k\notag \\[5pt] &=\sum _{v\in S} \sum _{w\in S} \left ( (1-p_v-p_w)^k + ((1-p_v-p_w+r(v,w))^k-(1-p_v-p_w)^k)\right )\notag \\[5pt] &= \sum _{v\in S} \sum _{w\in S} \left ( (1-p_v-p_w)^k +r(v,w)\sum _{i=0}^{k-1}(1-p_v-p_w)^i(1-p_v-p_w+r(v,w))^{k-1-i}\right ). \end{align*}
\begin{align*} {\mathbb{E}}_{\pi ^k}[X^2] &= \sum _{v\in S} \sum _{w\in S} (1-p_v-p_w+r(v,w))^k\notag \\[5pt] &=\sum _{v\in S} \sum _{w\in S} \left ( (1-p_v-p_w)^k + ((1-p_v-p_w+r(v,w))^k-(1-p_v-p_w)^k)\right )\notag \\[5pt] &= \sum _{v\in S} \sum _{w\in S} \left ( (1-p_v-p_w)^k +r(v,w)\sum _{i=0}^{k-1}(1-p_v-p_w)^i(1-p_v-p_w+r(v,w))^{k-1-i}\right ). \end{align*}
Since
![]() $2p^2k \lt 1$
and
$2p^2k \lt 1$
and
![]() $k\geq 2$
, we have
$k\geq 2$
, we have
![]() $1- p_v -p_w \geq 1-2p \gt 0$
. Additionally we have
$1- p_v -p_w \geq 1-2p \gt 0$
. Additionally we have
![]() $ r(v,w)\leq \min (p_v,p_w)$
and so
$ r(v,w)\leq \min (p_v,p_w)$
and so
![]() $1- p_v -p_w+r(v,w)\leq 1- \max \{p_v,p_w\} \leq 1$
. Thus
$1- p_v -p_w+r(v,w)\leq 1- \max \{p_v,p_w\} \leq 1$
. Thus
 \begin{align} {\mathbb{E}}_{\pi ^k}[X^2] &\leq \sum _{v\in S} \sum _{w\in S} \left ( (1-p_v-p_w)^k +r(v,w) \cdot k\right )\notag \\[5pt] &\leq \sum _{v\in S} \sum _{w\in S} e^{-kp_v-kp_w} +\left (\sum _{v\in S} \sum _{w\in S} r(v,w)\right ) \cdot k\notag \\[5pt] &= \left (\sum _{v\in S}e^{-kp_v} \right )^2+ {\mathbb{E}}_{\pi }[R(t)^2]\cdot k. \end{align}
\begin{align} {\mathbb{E}}_{\pi ^k}[X^2] &\leq \sum _{v\in S} \sum _{w\in S} \left ( (1-p_v-p_w)^k +r(v,w) \cdot k\right )\notag \\[5pt] &\leq \sum _{v\in S} \sum _{w\in S} e^{-kp_v-kp_w} +\left (\sum _{v\in S} \sum _{w\in S} r(v,w)\right ) \cdot k\notag \\[5pt] &= \left (\sum _{v\in S}e^{-kp_v} \right )^2+ {\mathbb{E}}_{\pi }[R(t)^2]\cdot k. \end{align}
Recall the Paley-Zygmund inequality: for any non-negative random variable
![]() $X$
,
$X$
,
![]() ${\mathbb{P}}_{\pi ^k}[X\gt 0 ] \geq {\mathbb{E}}_{\pi ^k} [X]^2/{\mathbb{E}}_{\pi ^k} [X^2]$
. Inserting (10) and (11) into the (inverted) fraction
${\mathbb{P}}_{\pi ^k}[X\gt 0 ] \geq {\mathbb{E}}_{\pi ^k} [X]^2/{\mathbb{E}}_{\pi ^k} [X^2]$
. Inserting (10) and (11) into the (inverted) fraction
![]() $\frac{{\mathbb{E}}_{\pi ^k} \left [X^2\right ]}{{\mathbb{E}}_{\pi ^k} \left [X\right ]^2}$
gives
$\frac{{\mathbb{E}}_{\pi ^k} \left [X^2\right ]}{{\mathbb{E}}_{\pi ^k} \left [X\right ]^2}$
gives
Finally, we claim that
![]() ${\mathbb{E}}_{\pi } [R(t)^2] \leq 2p^2 |S|(\!\min _{v \in S} \pi (v))^{-1}$
, therefore
${\mathbb{E}}_{\pi } [R(t)^2] \leq 2p^2 |S|(\!\min _{v \in S} \pi (v))^{-1}$
, therefore
 \begin{equation*} \frac {{\mathbb{E}}_{\pi ^k} \left [X^2\right ]}{{\mathbb{E}}_{\pi ^k} \left [X\right ]^2} \leq \frac {1}{(1-p^2k)^2}+ \frac {2kp^2e^{2kp}|S|/(\!\min _{v \in S} \pi (v))}{|S|^2(1-p^2k)^2} \leq \frac {1+ \frac {2kp^2e^{2kp}}{|S|\min _{v \in S} \pi (v)}}{(1-p^2k)^2} \end{equation*}
\begin{equation*} \frac {{\mathbb{E}}_{\pi ^k} \left [X^2\right ]}{{\mathbb{E}}_{\pi ^k} \left [X\right ]^2} \leq \frac {1}{(1-p^2k)^2}+ \frac {2kp^2e^{2kp}|S|/(\!\min _{v \in S} \pi (v))}{|S|^2(1-p^2k)^2} \leq \frac {1+ \frac {2kp^2e^{2kp}}{|S|\min _{v \in S} \pi (v)}}{(1-p^2k)^2} \end{equation*}
Now since
![]() ${\mathbb{P}}_{\pi ^k}\!\left[ \tau _{\mathsf{cov}}^{(k)} \leq t \right] = 1 - {\mathbb{P}}_{\pi ^k}\!\left[ \tau _{\mathsf{cov}}^{(k)} \gt t \right] \leq 1 - {\mathbb{E}}_{\pi ^k} [X]^2/{\mathbb{E}}_{\pi ^k} [X^2]$
we have
${\mathbb{P}}_{\pi ^k}\!\left[ \tau _{\mathsf{cov}}^{(k)} \leq t \right] = 1 - {\mathbb{P}}_{\pi ^k}\!\left[ \tau _{\mathsf{cov}}^{(k)} \gt t \right] \leq 1 - {\mathbb{E}}_{\pi ^k} [X]^2/{\mathbb{E}}_{\pi ^k} [X^2]$
we have
 \begin{equation*}{\mathbb{P}}_{\pi ^k}\!\left [ \tau _{\mathsf {cov}}^{(k)} \leq t\right ] \leq 1 - \frac {(1-p^2k)^2}{1+ \frac {2kp^2e^{2kp}}{|S|\min _{v \in S} \pi (v)}}\leq 1 - (1-2p^2k)\left (1 - \frac {2kp^2e^{2kp}}{|S|\min _{v \in S} \pi (v)} \right ), \end{equation*}
\begin{equation*}{\mathbb{P}}_{\pi ^k}\!\left [ \tau _{\mathsf {cov}}^{(k)} \leq t\right ] \leq 1 - \frac {(1-p^2k)^2}{1+ \frac {2kp^2e^{2kp}}{|S|\min _{v \in S} \pi (v)}}\leq 1 - (1-2p^2k)\left (1 - \frac {2kp^2e^{2kp}}{|S|\min _{v \in S} \pi (v)} \right ), \end{equation*}
since
![]() $\frac{1}{1+x}\geq 1-x$
for any
$\frac{1}{1+x}\geq 1-x$
for any
![]() $x\geq 0$
. Now, as
$x\geq 0$
. Now, as
![]() $|S|\min _{v \in S} \pi (v)\leq 1$
we have
$|S|\min _{v \in S} \pi (v)\leq 1$
we have
which concludes the main proof. To prove the claim, first observe that
 \begin{equation} {\mathbb{E}}_{\pi } \!\left [R(t)^2\right ] = {\mathbb{E}}_{\pi } \!\left [\sum _{v\in S}\sum _{w\in S} \textbf{1}(\tau _v\leq t )\textbf{1}(\tau _w\leq t )\right ] = \sum _{v\in S}\sum _{w\in S} {\mathbb{P}}_{\pi }\!\left [\tau _v\leq t, \tau _w\leq t\right ]. \end{equation}
\begin{equation} {\mathbb{E}}_{\pi } \!\left [R(t)^2\right ] = {\mathbb{E}}_{\pi } \!\left [\sum _{v\in S}\sum _{w\in S} \textbf{1}(\tau _v\leq t )\textbf{1}(\tau _w\leq t )\right ] = \sum _{v\in S}\sum _{w\in S} {\mathbb{P}}_{\pi }\!\left [\tau _v\leq t, \tau _w\leq t\right ]. \end{equation}
Now, by the Markov property, for any pair
![]() $(v,w)\in V^2$
we have
$(v,w)\in V^2$
we have
Thus by inserting the bound from (13) into (12) we have
 \begin{align*} {\mathbb{E}}_{\pi } \!\left [R(t)^2\right ] &\leq p\sum _{v\in S}\sum _{w\in S}{\mathbb{P}}_{v}\!\left [\tau _w\leq t\right ] + p\sum _{w\in S}\sum _{v\in S}{\mathbb{P}}_{w}\!\left [\tau _v\leq t\right ] \\[5pt] &\leq p\sum _{v\in S} {\mathbb{E}}_{v} \left [R(t)\right ]+p\sum _{w\in S}{\mathbb{E}}_{w} \left [R(t)\right ]\nonumber \\[5pt] &\leq p\sum _{v\in S} {\mathbb{E}}_{v} \left [R(t)\right ]\cdot \pi (v)\cdot \left(\!\min _{v \in S} \pi (v)\right)^{-1}+p\sum _{w\in S}{\mathbb{E}}_{w} \left [R(t)\right ]\cdot \pi (w)\cdot \left(\!\min _{v \in S} \pi (v)\right)^{-1}\nonumber \\[5pt] &\leq 2p{\mathbb{E}}_{\pi } \!\left [R(t)\right ](\!\min _{v \in S} \pi (v))^{-1}\\[5pt] &\leq 2p^2 |S|(\!\min _{v \in S} \pi (v))^{-1}, \end{align*}
\begin{align*} {\mathbb{E}}_{\pi } \!\left [R(t)^2\right ] &\leq p\sum _{v\in S}\sum _{w\in S}{\mathbb{P}}_{v}\!\left [\tau _w\leq t\right ] + p\sum _{w\in S}\sum _{v\in S}{\mathbb{P}}_{w}\!\left [\tau _v\leq t\right ] \\[5pt] &\leq p\sum _{v\in S} {\mathbb{E}}_{v} \left [R(t)\right ]+p\sum _{w\in S}{\mathbb{E}}_{w} \left [R(t)\right ]\nonumber \\[5pt] &\leq p\sum _{v\in S} {\mathbb{E}}_{v} \left [R(t)\right ]\cdot \pi (v)\cdot \left(\!\min _{v \in S} \pi (v)\right)^{-1}+p\sum _{w\in S}{\mathbb{E}}_{w} \left [R(t)\right ]\cdot \pi (w)\cdot \left(\!\min _{v \in S} \pi (v)\right)^{-1}\nonumber \\[5pt] &\leq 2p{\mathbb{E}}_{\pi } \!\left [R(t)\right ](\!\min _{v \in S} \pi (v))^{-1}\\[5pt] &\leq 2p^2 |S|(\!\min _{v \in S} \pi (v))^{-1}, \end{align*}
as claimed.
4. Mixing few walks to cover many vertices
In this section, we present several bounds on
![]() $t_{\mathsf{cov}}^{(k)}$
, the multiple cover time from worst-case start vertices, based on
$t_{\mathsf{cov}}^{(k)}$
, the multiple cover time from worst-case start vertices, based on
![]() $t_{\mathsf{cov}}^{(k)}(\pi )$
, the multiple cover time from stationarity, and a new notion that we call partial mixing time. The intuition behind this is that on many graphs such as cycles or binary trees, only a certain number, say
$t_{\mathsf{cov}}^{(k)}(\pi )$
, the multiple cover time from stationarity, and a new notion that we call partial mixing time. The intuition behind this is that on many graphs such as cycles or binary trees, only a certain number, say
![]() $\tilde{k}$
out of
$\tilde{k}$
out of
![]() $k$
walks will be able to reach vertices that are “far away” from their start vertex. That means covering the whole graph
$k$
walks will be able to reach vertices that are “far away” from their start vertex. That means covering the whole graph
![]() $G$
hinges on how quickly these
$G$
hinges on how quickly these
![]() $\tilde{k}$
“mixed” walks cover
$\tilde{k}$
“mixed” walks cover
![]() $G$
. However, we also need to take into account the number of steps needed to “mix” those. Theorem 4.7 makes this intuition more precise and suggests that the best strategy for covering a graph might be when
$G$
. However, we also need to take into account the number of steps needed to “mix” those. Theorem 4.7 makes this intuition more precise and suggests that the best strategy for covering a graph might be when
![]() $\tilde{k}$
is chosen so that the time to mix
$\tilde{k}$
is chosen so that the time to mix
![]() $\tilde{k}$
out of
$\tilde{k}$
out of
![]() $k$
walks and the stationary cover time of
$k$
walks and the stationary cover time of
![]() $\tilde{k}$
walks are approximately equal. As in the previous section we shall first state our results before proving them in the final two subsections.
$\tilde{k}$
walks are approximately equal. As in the previous section we shall first state our results before proving them in the final two subsections.
4.1. Two notions of mixing for multiple random walks
We begin by introducing the notion of partial mixing time. For any graph
![]() $G$
, and any
$G$
, and any
![]() $1 \leq \tilde{k} \lt k$
, we define the partial mixing time:
$1 \leq \tilde{k} \lt k$
, we define the partial mixing time:
 \begin{equation} \begin{aligned} t_{\mathsf{mix}}^{(\tilde{k},k)}(G) &= \inf \left \{t \geq 1 \;:\; \textit{there exists an SST }\tau \text{ such that }\min _{v\in V}{\mathbb{P}}_{v}\!\left [\tau \leq t\right ] \geq \tilde{k}/k \right \}\\[5pt] &= \inf \left \{t \geq 1 \;:\; s(t)\leq 1-\tilde k/k \right \} . \end{aligned} \end{equation}
\begin{equation} \begin{aligned} t_{\mathsf{mix}}^{(\tilde{k},k)}(G) &= \inf \left \{t \geq 1 \;:\; \textit{there exists an SST }\tau \text{ such that }\min _{v\in V}{\mathbb{P}}_{v}\!\left [\tau \leq t\right ] \geq \tilde{k}/k \right \}\\[5pt] &= \inf \left \{t \geq 1 \;:\; s(t)\leq 1-\tilde k/k \right \} . \end{aligned} \end{equation}
where SST stands for strong stationary time, and
![]() $s(t)$
is the separation distance (see Section 2). We note that the two definitions above are equivalent by the following result.
$s(t)$
is the separation distance (see Section 2). We note that the two definitions above are equivalent by the following result.
Proposition 4.1. ([Reference Aldous and Diaconis1], Proposition 3.2). If
![]() $\sigma$
is an SST then
$\sigma$
is an SST then
![]() ${\mathbb{P}} [\sigma \gt t]\geq s(t)$
for any
${\mathbb{P}} [\sigma \gt t]\geq s(t)$
for any
![]() $t\geq 0$
. Furthermore there exists an SST for which equality holds.
$t\geq 0$
. Furthermore there exists an SST for which equality holds.
Finally, we can rewrite the second definition based on
![]() $s(t)$
as follows:
$s(t)$
as follows:
This notion of mixing, based on the idea of separation distance and strong stationary times for single walks, will be useful for establishing an upper bound on the worst-case cover time. For lower bounds on the cover time by multiple walk we will now introduce another notion of mixing for multiple random walks in terms of hitting probabilities of large sets. Before doing so, we recall a fundamental connection for single random walks which links mixing times with hitting times of large sets. In particular, let
then the following theorem shows this large-set hitting time is equivalent to the mixing time.
Theorem 4.2. ([Reference Oliveira52] and independently [Reference Peres and Sousi54]). Let
![]() $\alpha \lt 1/2$
. Then there exist positive constants
$\alpha \lt 1/2$
. Then there exist positive constants
![]() $c(\alpha )$
and
$c(\alpha )$
and
![]() $C(\alpha )$
so that for every reversible chain
$C(\alpha )$
so that for every reversible chain
Inspired by that fundamental result, we introduce the following quantity, which will be used to lower bound the cover time of multiple random walks,
 \begin{align} t_{\mathsf{large-hit}}^{(\tilde{k},k)}(G) = \min \left \{t \geq 1: \min _{u \in V, S \subseteq V : \pi (S) \geq 1/4} {\mathbb{P}}_{u}\!\left [ \tau _{S} \leq t\right ] \geq \frac{\tilde{k}}{k} \right \}. \end{align}
\begin{align} t_{\mathsf{large-hit}}^{(\tilde{k},k)}(G) = \min \left \{t \geq 1: \min _{u \in V, S \subseteq V : \pi (S) \geq 1/4} {\mathbb{P}}_{u}\!\left [ \tau _{S} \leq t\right ] \geq \frac{\tilde{k}}{k} \right \}. \end{align}
Note that both notions of mixing times are only defined for
![]() $\tilde k\lt k$
. However, by the union bound, there exists a
$\tilde k\lt k$
. However, by the union bound, there exists a
![]() $C\lt \infty$
such that if we run
$C\lt \infty$
such that if we run
![]() $k$
walks for
$k$
walks for
![]() $Ct_{\mathsf{mix}} \log k$
steps then all
$Ct_{\mathsf{mix}} \log k$
steps then all
![]() $k$
walks will be close to stationarity in terms of TV-distance. Our next lemma generalises this fact.
$k$
walks will be close to stationarity in terms of TV-distance. Our next lemma generalises this fact.
Lemma 4.3.
There exists a constant
![]() $C\lt \infty$
such that for any graph and
$C\lt \infty$
such that for any graph and
![]() $1\leq \tilde{k}\lt k$
we have
$1\leq \tilde{k}\lt k$
we have
-
(i)
 $\displaystyle{t_{\mathsf{mix}}^{(\tilde{k},k)} \leq 2\cdot t_{\mathsf{mix}}\cdot \left \lceil \log _2 \left (\frac{2k}{k-\tilde{k}}\right )\right \rceil }$
,
$\displaystyle{t_{\mathsf{mix}}^{(\tilde{k},k)} \leq 2\cdot t_{\mathsf{mix}}\cdot \left \lceil \log _2 \left (\frac{2k}{k-\tilde{k}}\right )\right \rceil }$
, -
(ii)
 $\displaystyle{t_{\mathsf{large-hit}}^{(\tilde{k},k)} \leq C\cdot t_{\mathsf{mix}} \cdot \left \lceil \log \left (\frac{k}{k-\tilde{k}}\right )\right \rceil }$
.
$\displaystyle{t_{\mathsf{large-hit}}^{(\tilde{k},k)} \leq C\cdot t_{\mathsf{mix}} \cdot \left \lceil \log \left (\frac{k}{k-\tilde{k}}\right )\right \rceil }$
.
The partial mixing time can be bounded from below quite simply by mixing time.
Lemma 4.4.
For any graph and
![]() $1\leq \tilde{k}\lt k$
we have
$1\leq \tilde{k}\lt k$
we have
 \begin{equation*}t_{\mathsf {mix}}^{(\tilde {k},k)} \geq t_{\mathsf {mix}} \!\left (1-\frac {\tilde {k}}{k}\right ).\end{equation*}
\begin{equation*}t_{\mathsf {mix}}^{(\tilde {k},k)} \geq t_{\mathsf {mix}} \!\left (1-\frac {\tilde {k}}{k}\right ).\end{equation*}
Proof. This follows since
![]() $d_{\textrm{TV}}(t)\leq s(t)$
holds for any
$d_{\textrm{TV}}(t)\leq s(t)$
holds for any
![]() $t\geq 0$
by [Reference Levin, Peres and Wilmer42, Lemma 6.3].
$t\geq 0$
by [Reference Levin, Peres and Wilmer42, Lemma 6.3].
We would prefer a bound in terms of
![]() $t_{\mathsf{mix}}\;:\!=\;t_{\mathsf{mix}}(1/4)$
instead of
$t_{\mathsf{mix}}\;:\!=\;t_{\mathsf{mix}}(1/4)$
instead of
![]() $t_{\mathsf{mix}}(1-\tilde{k}/k)$
as the former is easier to compute for most graphs. The following lemma establishes such a lower bound for both notions of mixing time at the cost of a
$t_{\mathsf{mix}}(1-\tilde{k}/k)$
as the former is easier to compute for most graphs. The following lemma establishes such a lower bound for both notions of mixing time at the cost of a
![]() $\tilde{k}/k$
factor.
$\tilde{k}/k$
factor.
Lemma 4.5.
There exists some constant
![]() $c\gt 0$
such that for any graph and
$c\gt 0$
such that for any graph and
![]() $1\leq \tilde{k}\lt k$
we have
$1\leq \tilde{k}\lt k$
we have
-
(i)
 $\displaystyle{t_{\mathsf{mix}}^{(\tilde{k},k)} \geq c\cdot \frac{\tilde{k}}{k}\cdot t_{\mathsf{mix}}}$
,
$\displaystyle{t_{\mathsf{mix}}^{(\tilde{k},k)} \geq c\cdot \frac{\tilde{k}}{k}\cdot t_{\mathsf{mix}}}$
, -
(ii)
 $\displaystyle{t_{\mathsf{large-hit}}^{(\tilde{k},k)}\geq c\cdot \frac{\tilde{k}}{k}\cdot t_{\mathsf{mix}}}$
.
$\displaystyle{t_{\mathsf{large-hit}}^{(\tilde{k},k)}\geq c\cdot \frac{\tilde{k}}{k}\cdot t_{\mathsf{mix}}}$
.
We leave as an open problem whether our two notions of mixing for multiple random walks are equivalent up to constants, but the next result gives partial progress in one direction.
Lemma 4.6.
For any graph and
![]() $1\leq \tilde{k}\lt k/4$
we have
$1\leq \tilde{k}\lt k/4$
we have
4.2. Upper and lower bounds on cover time by partial mixing
Armed with our new notions of mixing time for multiple random walks from Section 4.1, we can now use them to prove upper and lower bounds on the worst-case cover time in terms of stationary cover times and partial mixing times. We begin with the upper bound.
Theorem 4.7.
For any graph
![]() $G$
and any
$G$
and any
![]() $1 \leq k \leq n$
,
$1 \leq k \leq n$
,
This theorem improves on various results in [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5] and [Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19] which bound the worst-case cover time by mixing all
![]() $k$
walks, and it also generalises a previous result in [Reference Elsässer and Sauerwald20, Lemma 3.1], where most walks were mixed, that is,
$k$
walks, and it also generalises a previous result in [Reference Elsässer and Sauerwald20, Lemma 3.1], where most walks were mixed, that is,
![]() $\tilde{k} = k/2$
.
$\tilde{k} = k/2$
.
We also prove a lower bound for cover times, however this involves the related definition of partial mixing time based on the hitting times of large sets.
Theorem 4.8.
For any graph
![]() $G$
with
$G$
with
![]() $\pi _{\max }=\max _{u} \pi (u)$
and any
$\pi _{\max }=\max _{u} \pi (u)$
and any
![]() $1 \leq k \leq n$
,
$1 \leq k \leq n$
,
Further, for any regular graph
![]() $G$
any
$G$
any
![]() $\gamma \gt 0$
fixed, there is a constant
$\gamma \gt 0$
fixed, there is a constant
![]() $C=C(\gamma )\gt 0$
such that
$C=C(\gamma )\gt 0$
such that
As we will see later, both Theorems 4.7 and 4.8 yield asymptotically tight (or tight up to logarithmic factors) upper and lower bounds for many concrete networks. To explain why this is often the case, note that both bounds include one non-increasing function in
![]() $\tilde{k}$
and one non-decreasing in function in
$\tilde{k}$
and one non-decreasing in function in
![]() $\tilde{k}$
. That means both bounds are optimised when the two functions are as close as possible. Then balancing the two functions in the upper bound asks for
$\tilde{k}$
. That means both bounds are optimised when the two functions are as close as possible. Then balancing the two functions in the upper bound asks for
![]() $\tilde{k}$
such that
$\tilde{k}$
such that
![]() $t_{\mathsf{mix}}^{(\tilde{k},k)} \approx t_{\mathsf{cov}}^{(\tilde{k})}(\pi )$
. Similarly, balancing the two functions in the first lower bound demands
$t_{\mathsf{mix}}^{(\tilde{k},k)} \approx t_{\mathsf{cov}}^{(\tilde{k})}(\pi )$
. Similarly, balancing the two functions in the first lower bound demands
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)} \approx n/\tilde{k}$
(assuming
$t_{\mathsf{large-hit}}^{(\tilde{k},k)} \approx n/\tilde{k}$
(assuming
![]() $\pi _{\max }=O(1/n)$
). Hence for any graph
$\pi _{\max }=O(1/n)$
). Hence for any graph
![]() $G$
where
$G$
where
![]() $t_{\mathsf{mix}}^{(\tilde{k},k)} \approx t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
, and also
$t_{\mathsf{mix}}^{(\tilde{k},k)} \approx t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
, and also
![]() $t_{\mathsf{cov}}^{(\tilde{k})}(\pi ) \approx n/\tilde{k}$
, the upper and lower bounds will be close. This turns out to be the case for many networks, as we will demonstrate in Section 5.
$t_{\mathsf{cov}}^{(\tilde{k})}(\pi ) \approx n/\tilde{k}$
, the upper and lower bounds will be close. This turns out to be the case for many networks, as we will demonstrate in Section 5.
One exception where Theorem 4.8 is far from tight is the cycle, we shall also prove a min-max theorem but with a different notion of partial cover time which is tight for the cycle.
For a set
![]() $S\subseteq V$
, we let
$S\subseteq V$
, we let
![]() $\tau ^{(k)}_{\mathsf{cov}}(S)$
be the first time that every vertex in
$\tau ^{(k)}_{\mathsf{cov}}(S)$
be the first time that every vertex in
![]() $S$
has been visited by at least one of the
$S$
has been visited by at least one of the
![]() $k$
walks, thus
$k$
walks, thus
![]() $\tau _{\mathsf{cov}}^{(k)}(V) = \tau ^{(k)}_{\mathsf{cov}}$
. Then we define the set cover time
$\tau _{\mathsf{cov}}^{(k)}(V) = \tau ^{(k)}_{\mathsf{cov}}$
. Then we define the set cover time
where the first minimum is over all sets
![]() $S\subseteq V$
satisfying
$S\subseteq V$
satisfying
![]() $\pi (S)\geq 1/4$
and the second is over all probability distributions
$\pi (S)\geq 1/4$
and the second is over all probability distributions
![]() $\mu$
on the set
$\mu$
on the set
![]() $\partial S=\{x\in S \;:\; \text{exists }y\in S^c, \;xy \in E \}$
.
$\partial S=\{x\in S \;:\; \text{exists }y\in S^c, \;xy \in E \}$
.
Theorem 4.9.
For any graph
![]() $G$
and any
$G$
and any
![]() $1 \leq k \leq n$
,
$1 \leq k \leq n$
,
4.3. Geometric lower bounds on the large-hit and large-cover times
We will now derive two useful lower bounds on
![]() $ t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
; one based on the conductance of the graph, and a second one based on the distance to a large set the random walk needs to hit.
$ t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
; one based on the conductance of the graph, and a second one based on the distance to a large set the random walk needs to hit.
For two sets
![]() $A,B \subseteq V$
the ergodic flow
$A,B \subseteq V$
the ergodic flow
![]() $Q(A,B)$
is given by
$Q(A,B)$
is given by
![]() $Q(A,B) = \sum _{a\in A, b\in B} \pi (a) P_{a,b},$
where
$Q(A,B) = \sum _{a\in A, b\in B} \pi (a) P_{a,b},$
where
![]() $P$
denotes the transition matrix of a (lazy) single random walk. We define the conductance
$P$
denotes the transition matrix of a (lazy) single random walk. We define the conductance
![]() $\Phi (S)$
of a set
$\Phi (S)$
of a set
![]() $S\subseteq V$
with
$S\subseteq V$
with
![]() $\pi (S) \in (0,1/2]$
to be
$\pi (S) \in (0,1/2]$
to be
Lemma 4.10.
For any graph
![]() $G$
with conductance
$G$
with conductance
![]() $\Phi (G)$
, and any
$\Phi (G)$
, and any
![]() $1 \leq \tilde{k} \leq k$
, we have
$1 \leq \tilde{k} \leq k$
, we have
We remark that a similar bound to that in Lemma 4.10 was used implicitly in [Reference Sauerwald, Richa and Guerraoui58, Proof of Theorem 1.1], which proved
![]() $t_{\mathsf{cov}}^{(k)} \geq \sqrt{ \frac{n}{k \cdot \Phi (G)}}$
.
$t_{\mathsf{cov}}^{(k)} \geq \sqrt{ \frac{n}{k \cdot \Phi (G)}}$
.
The next lemmas are needed to apply Theorems 4.8 & 4.9 to cycles/tori.
Lemma 4.11.
Let
![]() $G$
be a
$G$
be a
![]() $d$
-dimensional torus with constant
$d$
-dimensional torus with constant
![]() $d\geq 2$
(or cycle,
$d\geq 2$
(or cycle,
![]() $d=1$
). Then, for any
$d=1$
). Then, for any
![]() $u \in V$
,
$u \in V$
,
![]() $S\subseteq V$
satisfying
$S\subseteq V$
satisfying
![]() $|S| \geq n/4$
, and
$|S| \geq n/4$
, and
![]() $\tilde{k} \leq k/2$
, we have
$\tilde{k} \leq k/2$
, we have
 \begin{equation*} t_{\mathsf {large-hit}}^{(\tilde {k},k)} = \Omega \left ( \frac {\textrm {dist}(u,S)^2}{\log\!( k/\tilde {k}) } \right ). \end{equation*}
\begin{equation*} t_{\mathsf {large-hit}}^{(\tilde {k},k)} = \Omega \left ( \frac {\textrm {dist}(u,S)^2}{\log\!( k/\tilde {k}) } \right ). \end{equation*}
Lemma 4.12.
Let
![]() $S \subseteq V$
be a subset of vertices with
$S \subseteq V$
be a subset of vertices with
![]() $\pi (S) \geq 1/4$
,
$\pi (S) \geq 1/4$
,
![]() $t \geq 2$
be an integer and
$t \geq 2$
be an integer and
![]() $k \geq 100$
such that
$k \geq 100$
such that
![]() $\sum _{s=0}^{t} P_{u,u}^s \geq 32 \cdot t \cdot \pi (u) \cdot k$
for all
$\sum _{s=0}^{t} P_{u,u}^s \geq 32 \cdot t \cdot \pi (u) \cdot k$
for all
![]() $u \in S$
. Then, for any distribution
$u \in S$
. Then, for any distribution
![]() $\mu$
on
$\mu$
on
![]() $S$
,
$S$
,
4.4. Proofs of lemmas in Section 4.1
Proof of Lemma
4.3. We start with Item (i). Let
![]() $\bar d_{\textrm{TV}}(t) = \max _{x,y \in V} \|P_{x,\cdot }^t -P_{y,\cdot }^t\|_{\textrm{TV}}$
. Then
$\bar d_{\textrm{TV}}(t) = \max _{x,y \in V} \|P_{x,\cdot }^t -P_{y,\cdot }^t\|_{\textrm{TV}}$
. Then
hold for any integers
![]() $t,\ell \geq 0$
by Lemmas 4.11, 4.12 and 19.3, respectively, of [Reference Levin, Peres and Wilmer42].
$t,\ell \geq 0$
by Lemmas 4.11, 4.12 and 19.3, respectively, of [Reference Levin, Peres and Wilmer42].
Thus if we take
![]() $\ell = \lceil \log _{2} (2k/(k-\tilde{k}) ) \rceil$
and
$\ell = \lceil \log _{2} (2k/(k-\tilde{k}) ) \rceil$
and
![]() $t = t_{\mathsf{mix}}(1/4)$
then we have
$t = t_{\mathsf{mix}}(1/4)$
then we have
 \begin{equation*} s(2\ell t) \leq 1-(1-\bar d_{\textrm{TV}}(\ell t))^2 \leq 2\bar d_{\textrm{TV}}(\ell t)\leq 2\bar d_{\textrm{TV}}( t)^\ell \leq 2\cdot ( 2 d_{\textrm{TV}}( t))^\ell \leq 2\cdot \left (\frac {1}{2}\right )^{\log _{2}\left (\frac {2k}{k-\tilde {k}}\right )} \leq 1- \frac {\tilde {k}}{k}, \end{equation*}
\begin{equation*} s(2\ell t) \leq 1-(1-\bar d_{\textrm{TV}}(\ell t))^2 \leq 2\bar d_{\textrm{TV}}(\ell t)\leq 2\bar d_{\textrm{TV}}( t)^\ell \leq 2\cdot ( 2 d_{\textrm{TV}}( t))^\ell \leq 2\cdot \left (\frac {1}{2}\right )^{\log _{2}\left (\frac {2k}{k-\tilde {k}}\right )} \leq 1- \frac {\tilde {k}}{k}, \end{equation*}
it follows that
![]() $ t_{\mathsf{mix}}^{(\tilde{k},k)}\leq 2\ell t \leq 2 t_{\mathsf{mix}} \left\lceil \log _{2} (2k/(k-\tilde{k}) ) \right\rceil$
.
$ t_{\mathsf{mix}}^{(\tilde{k},k)}\leq 2\ell t \leq 2 t_{\mathsf{mix}} \left\lceil \log _{2} (2k/(k-\tilde{k}) ) \right\rceil$
.
For Item (ii), by the Markov property for any non-negative integers
![]() $\ell$
and
$\ell$
and
![]() $t$
, we have
$t$
, we have
By Markov’s inequality we have
![]() $\max _{x\in V, S\subseteq V, \pi (S)\geq 1/4}{\mathbb{P}}_{x}[\tau _S\gt 2t_{\mathsf{H}} ]\leq 1/2$
and by Theorem 4.2 there exists some
$\max _{x\in V, S\subseteq V, \pi (S)\geq 1/4}{\mathbb{P}}_{x}[\tau _S\gt 2t_{\mathsf{H}} ]\leq 1/2$
and by Theorem 4.2 there exists some
![]() $C$
such that
$C$
such that
![]() $t_{\mathsf{H}}\leq Ct_{\mathsf{mix}}$
. Thus, if we take
$t_{\mathsf{H}}\leq Ct_{\mathsf{mix}}$
. Thus, if we take
![]() $T = 2Ct_{\mathsf{mix}} \cdot \lceil \log _2 (k/(k-\tilde{k}) ) \rceil$
, then
$T = 2Ct_{\mathsf{mix}} \cdot \lceil \log _2 (k/(k-\tilde{k}) ) \rceil$
, then
 \begin{equation*}\max _{x\in V, S\subseteq V, \pi (S)\geq 1/4}{\mathbb{P}}_{x}\!\left [\tau _S\gt T\right ]\leq \left (\max _{x\in V, S\subseteq V, \pi (S)\geq 1/4}{\mathbb{P}}_{x}\!\left [\tau _S\gt 2t_{\mathsf {H} }\right ]\right )^{\log _2\left (k/(k-\tilde {k})\right )} \leq 1 -\frac {\tilde {k}}{k}. \end{equation*}
\begin{equation*}\max _{x\in V, S\subseteq V, \pi (S)\geq 1/4}{\mathbb{P}}_{x}\!\left [\tau _S\gt T\right ]\leq \left (\max _{x\in V, S\subseteq V, \pi (S)\geq 1/4}{\mathbb{P}}_{x}\!\left [\tau _S\gt 2t_{\mathsf {H} }\right ]\right )^{\log _2\left (k/(k-\tilde {k})\right )} \leq 1 -\frac {\tilde {k}}{k}. \end{equation*}
It follows that
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)} \leq T = C't_{\mathsf{mix}} \lceil \log\!(k/(k-\tilde{k}) ) \rceil$
for some
$t_{\mathsf{large-hit}}^{(\tilde{k},k)} \leq T = C't_{\mathsf{mix}} \lceil \log\!(k/(k-\tilde{k}) ) \rceil$
for some
![]() $C'\lt \infty$
.
$C'\lt \infty$
.
Proof of Lemma
4.5. For Item (i), if we let
![]() $\ell = t_{\mathsf{mix}}^{(\tilde{k},k)}+1$
then the separation distances satisfies
$\ell = t_{\mathsf{mix}}^{(\tilde{k},k)}+1$
then the separation distances satisfies
![]() $s(\ell )\leq 1-\tilde{k}/k$
. Thus, by the definition of separation distance, for any pair of vertices
$s(\ell )\leq 1-\tilde{k}/k$
. Thus, by the definition of separation distance, for any pair of vertices
![]() $x,y\in V$
we have
$x,y\in V$
we have
![]() $P_{x,y}^\ell \geq (\tilde{k}/k) \cdot \pi (y)$
. Thus for any
$P_{x,y}^\ell \geq (\tilde{k}/k) \cdot \pi (y)$
. Thus for any
![]() $x\in V$
and set
$x\in V$
and set
![]() $S\subseteq V$
satisfying
$S\subseteq V$
satisfying
![]() $\pi (S)\geq 1/4$
we have
$\pi (S)\geq 1/4$
we have
 \begin{equation} {\mathbb{P}}_{x}\!\left [\tau _S \leq \ell \right ]\geq \sum _{y\in S} P_{x,y}^\ell \geq \sum _{y\in S} \frac{\tilde{k}}{k} \cdot \pi (y) = \frac{\tilde{k}}{k}\sum _{y\in S} \pi (y) = \frac{\tilde{k}}{k}\pi (S)\geq \frac{\tilde{k}}{4k}. \end{equation}
\begin{equation} {\mathbb{P}}_{x}\!\left [\tau _S \leq \ell \right ]\geq \sum _{y\in S} P_{x,y}^\ell \geq \sum _{y\in S} \frac{\tilde{k}}{k} \cdot \pi (y) = \frac{\tilde{k}}{k}\sum _{y\in S} \pi (y) = \frac{\tilde{k}}{k}\pi (S)\geq \frac{\tilde{k}}{4k}. \end{equation}
Since (17) holds for all
![]() $x\in V$
and
$x\in V$
and
![]() $S\subseteq V$
where
$S\subseteq V$
where
![]() $\pi (S)\geq 1/4$
, we have
$\pi (S)\geq 1/4$
, we have
![]() $ t_{\mathsf{H}} \leq \ell \cdot (4k/\tilde{k})$
, as
$ t_{\mathsf{H}} \leq \ell \cdot (4k/\tilde{k})$
, as
![]() $\tau _S$
is stochastically dominated by
$\tau _S$
is stochastically dominated by
![]() $\ell$
times the number of phases of length
$\ell$
times the number of phases of length
![]() $\ell$
before
$\ell$
before
![]() $S$
is hit. By Theorem 4.2 there exists a universal constant
$S$
is hit. By Theorem 4.2 there exists a universal constant
![]() $ C\lt \infty$
such that for any graph
$ C\lt \infty$
such that for any graph
![]() $t_{\mathsf{mix}} \leq C\cdot t_{\mathsf{H}}$
, thus
$t_{\mathsf{mix}} \leq C\cdot t_{\mathsf{H}}$
, thus
for some universal constant
![]() $C'\lt \infty$
as
$C'\lt \infty$
as
![]() $ t_{\mathsf{mix}}^{(\tilde{k},k)}\geq 1$
.
$ t_{\mathsf{mix}}^{(\tilde{k},k)}\geq 1$
.
For Item (ii), observe that if instead we set
![]() $ \ell = t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
then (17) still holds (in fact the stronger bound
$ \ell = t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
then (17) still holds (in fact the stronger bound
![]() ${\mathbb{P}}_{x}[\tau _S \leq \ell ] \geq \tilde{k}/k$
holds) and the rest of the proof goes through unchanged.
${\mathbb{P}}_{x}[\tau _S \leq \ell ] \geq \tilde{k}/k$
holds) and the rest of the proof goes through unchanged.
Proof of Lemma
4.6. If we let
![]() $\ell = t_{\mathsf{mix}}^{(4\tilde{k},k)}+1$
then
$\ell = t_{\mathsf{mix}}^{(4\tilde{k},k)}+1$
then
![]() $s(\ell )\leq 1-4\tilde{k}/k$
. So,
$s(\ell )\leq 1-4\tilde{k}/k$
. So,
![]() $P_{x,y}^\ell \geq (4\tilde{k}/k) \cdot \pi (y)$
for any pair of vertices
$P_{x,y}^\ell \geq (4\tilde{k}/k) \cdot \pi (y)$
for any pair of vertices
![]() $x,y\in V$
. Thus for any
$x,y\in V$
. Thus for any
![]() $x\in V$
and set
$x\in V$
and set
![]() $S\subseteq V$
satisfying
$S\subseteq V$
satisfying
![]() $\pi (S)\geq 1/4$
we have
$\pi (S)\geq 1/4$
we have
 \begin{equation*} {\mathbb{P}}_{x}\!\left [\tau _S \leq \ell \right ]\geq \sum _{y\in S} P_{x,y}^\ell \geq \sum _{y\in S} \frac {4\tilde {k}}{k} \cdot \pi (y) = \frac {4\tilde {k}}{k}\sum _{y\in S} \pi (y) = \frac {4\tilde {k}}{k}\pi (S)\geq \frac {\tilde {k}}{k}. \end{equation*}
\begin{equation*} {\mathbb{P}}_{x}\!\left [\tau _S \leq \ell \right ]\geq \sum _{y\in S} P_{x,y}^\ell \geq \sum _{y\in S} \frac {4\tilde {k}}{k} \cdot \pi (y) = \frac {4\tilde {k}}{k}\sum _{y\in S} \pi (y) = \frac {4\tilde {k}}{k}\pi (S)\geq \frac {\tilde {k}}{k}. \end{equation*}
Consequently, we have
![]() $ t_{\mathsf{large-hit}}^{(\tilde{k},k)}\leq \ell = t_{\mathsf{mix}}^{(4\tilde{k},k)} +1 \leq 2t_{\mathsf{mix}}^{(4\tilde{k},k)},$
as claimed since
$ t_{\mathsf{large-hit}}^{(\tilde{k},k)}\leq \ell = t_{\mathsf{mix}}^{(4\tilde{k},k)} +1 \leq 2t_{\mathsf{mix}}^{(4\tilde{k},k)},$
as claimed since
![]() $t_{\mathsf{mix}}^{(4\tilde{k},k)}\geq 1$
.
$t_{\mathsf{mix}}^{(4\tilde{k},k)}\geq 1$
.
4.5. Proofs of upper and lower bounds for covering via partial mixing
Proof of Theorem
4.7. Fix any
![]() $1 \leq \tilde{k} \lt k$
. It suffices to prove that with
$1 \leq \tilde{k} \lt k$
. It suffices to prove that with
![]() $k$
walks starting from arbitrary positions running for
$k$
walks starting from arbitrary positions running for
steps, we cover
![]() $G$
with probability at least
$G$
with probability at least
![]() $1/4$
. Consider a single walk
$1/4$
. Consider a single walk
![]() $X_1$
on
$X_1$
on
![]() $G$
starting from
$G$
starting from
![]() $v$
. From the definition of
$v$
. From the definition of
![]() $s_v(t)$
we have that at time
$s_v(t)$
we have that at time
![]() $T= t_{\mathsf{mix}}^{(\tilde k, k)}$
there exists a probability measure
$T= t_{\mathsf{mix}}^{(\tilde k, k)}$
there exists a probability measure
![]() $\nu _v$
on
$\nu _v$
on
![]() $V$
such that,
$V$
such that,
Now, note that (14) yields
![]() $(1-s_v(T))\geq \tilde k/k$
, therefore, we can generate
$(1-s_v(T))\geq \tilde k/k$
, therefore, we can generate
![]() $X_1(T)$
as follows: with probability
$X_1(T)$
as follows: with probability
![]() $1-s_v(T)\geq \tilde k/k$
we sample from
$1-s_v(T)\geq \tilde k/k$
we sample from
![]() $\pi$
, otherwise we sample from
$\pi$
, otherwise we sample from
![]() $\nu _v$
. If we now consider
$\nu _v$
. If we now consider
![]() $k$
independent walks, the number of walks that are sampled at time
$k$
independent walks, the number of walks that are sampled at time
![]() $T$
from
$T$
from
![]() $\pi$
has a binomial distribution
$\pi$
has a binomial distribution
![]() $\text{Bin}(k,\tilde{k}/k)$
with
$\text{Bin}(k,\tilde{k}/k)$
with
![]() $k$
trials and probability
$k$
trials and probability
![]() $\tilde k/k$
, whose expectation is
$\tilde k/k$
, whose expectation is
![]() $\tilde k$
. Since the expectation
$\tilde k$
. Since the expectation
![]() $\tilde{k}$
is an integer it is equal to the median. Thus, with probability at least
$\tilde{k}$
is an integer it is equal to the median. Thus, with probability at least
![]() $1/2$
, at least
$1/2$
, at least
![]() $\tilde k$
walks are sampled from the stationary distribution. Now, consider only the
$\tilde k$
walks are sampled from the stationary distribution. Now, consider only the
![]() $\tilde k$
independent walks starting from
$\tilde k$
independent walks starting from
![]() $\pi$
. After
$\pi$
. After
![]() $2t_{\mathsf{cov}}^{(\tilde k)}(\pi )$
steps, these walks will cover
$2t_{\mathsf{cov}}^{(\tilde k)}(\pi )$
steps, these walks will cover
![]() $G$
with probability at least
$G$
with probability at least
![]() $1/2$
, due to Markov’s inequality.
$1/2$
, due to Markov’s inequality.
We conclude that in
![]() $t$
time steps, from any starting configuration of the
$t$
time steps, from any starting configuration of the
![]() $k$
walks, the probability we cover the graph is at least
$k$
walks, the probability we cover the graph is at least
![]() $1/4$
. Hence in expectation, after (at most) 4 periods of length
$1/4$
. Hence in expectation, after (at most) 4 periods of length
![]() $t$
we cover the graph.
$t$
we cover the graph.
Proof of Theorem
4.8. By the definition of
![]() $ t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
, there exists a vertex
$ t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
, there exists a vertex
![]() $u$
and
$u$
and
![]() $S\subseteq V$
such that
$S\subseteq V$
such that
![]() ${\mathbb{P}}_{u}\!\left[\tau _{S}\leq t_{\mathsf{large-hit}}^{(\tilde{k},k)}-1 \right] \lt \tilde k/k$
. For such a vertex
${\mathbb{P}}_{u}\!\left[\tau _{S}\leq t_{\mathsf{large-hit}}^{(\tilde{k},k)}-1 \right] \lt \tilde k/k$
. For such a vertex
![]() $u$
, we consider
$u$
, we consider
![]() $k$
walks, all started from
$k$
walks, all started from
![]() $u$
, which run for
$u$
, which run for
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)}-1$
steps. It follows that the number of walks that hit
$t_{\mathsf{large-hit}}^{(\tilde{k},k)}-1$
steps. It follows that the number of walks that hit
![]() $S$
before time
$S$
before time
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
is dominated by a binomial distribution with parameters
$t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
is dominated by a binomial distribution with parameters
![]() $k$
and
$k$
and
![]() $p = \tilde k/k$
, whose expected value and median is
$p = \tilde k/k$
, whose expected value and median is
![]() $\tilde k$
. We conclude that with probability at least
$\tilde k$
. We conclude that with probability at least
![]() $1/2$
, at most
$1/2$
, at most
![]() $\tilde k$
walks hit
$\tilde k$
walks hit
![]() $S$
. Note that
$S$
. Note that
![]() $|S| \geq \pi (S)/\pi _{\max } \geq 1/(4 \pi _{\max })$
. Hence even if all
$|S| \geq \pi (S)/\pi _{\max } \geq 1/(4 \pi _{\max })$
. Hence even if all
![]() $\tilde{k}$
walks that reached
$\tilde{k}$
walks that reached
![]() $S$
before time
$S$
before time
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
were allowed to run for exactly
$t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
were allowed to run for exactly
![]() $1/(8 \tilde{k} \pi _{\max })-1$
steps (if a walk exits
$1/(8 \tilde{k} \pi _{\max })-1$
steps (if a walk exits
![]() $S$
, we can completely ignore the steps until it returns to
$S$
, we can completely ignore the steps until it returns to
![]() $S$
), then the total number of covered vertices in
$S$
), then the total number of covered vertices in
![]() $S$
would be at most
$S$
would be at most
which concludes the proof of the first bound.
For the second bound, we follow the first part of the proof before and consider again at most
![]() $ \tilde{k}$
walks that reach the set
$ \tilde{k}$
walks that reach the set
![]() $S$
. Let us denote by
$S$
. Let us denote by
![]() $\kappa$
the induced distribution over
$\kappa$
the induced distribution over
![]() $S$
upon hitting
$S$
upon hitting
![]() $S$
from
$S$
from
![]() $u$
for the first time. Now, each of the
$u$
for the first time. Now, each of the
![]() $\tilde{k}$
walks continues for another
$\tilde{k}$
walks continues for another
![]() $\ell =\lfloor \epsilon (n/\tilde{k}) \log\!(n) \rfloor$
steps, where
$\ell =\lfloor \epsilon (n/\tilde{k}) \log\!(n) \rfloor$
steps, where
![]() $0\lt \epsilon =\epsilon (\gamma ) \lt 1$
is a sufficiently small constant fixed later. We now define, for any
$0\lt \epsilon =\epsilon (\gamma ) \lt 1$
is a sufficiently small constant fixed later. We now define, for any
![]() $v \in S$
, the probability
$v \in S$
, the probability
![]() $ p_{v} = {\mathbb{P}}_{\kappa }[ \tau _v \leq \epsilon (n/\tilde{k}) \log n ].$
Observe that since a walk of length
$ p_{v} = {\mathbb{P}}_{\kappa }[ \tau _v \leq \epsilon (n/\tilde{k}) \log n ].$
Observe that since a walk of length
![]() $\ell$
can cover at most
$\ell$
can cover at most
![]() $\ell$
vertices, we have
$\ell$
vertices, we have
![]() $\sum _{v \in S} p_v \leq \ell$
. Further, define the set
$\sum _{v \in S} p_v \leq \ell$
. Further, define the set
![]() $\widetilde{S}= \{ v \in S \,:\, p_v \lt 8 \ell/n \}$
.
$\widetilde{S}= \{ v \in S \,:\, p_v \lt 8 \ell/n \}$
.
Since for every
![]() $v$
with
$v$
with
![]() $p_v\geq 8 \ell/n$
we have that
$p_v\geq 8 \ell/n$
we have that
![]() $np_v/(8 \ell )\geq 1$
and
$np_v/(8 \ell )\geq 1$
and
where the last inequality holds since
![]() $G$
is regular. Thus
$G$
is regular. Thus
![]() $\tilde{S} \geq |S|/2$
. Now, let
$\tilde{S} \geq |S|/2$
. Now, let
![]() $Z$
be the number of unvisited vertices in
$Z$
be the number of unvisited vertices in
![]() $\widetilde{S}$
after we run
$\widetilde{S}$
after we run
![]() $\tilde{k}$
random walks starting from
$\tilde{k}$
random walks starting from
![]() $\kappa$
. If
$\kappa$
. If
![]() $p_*=\max _{v\in \tilde{S}}p_v\lt 8\ell/n$
then, by definition and recalling that
$p_*=\max _{v\in \tilde{S}}p_v\lt 8\ell/n$
then, by definition and recalling that
![]() $\ell =\lfloor \epsilon (n/\tilde{k}) \log\!(n) \rfloor$
where
$\ell =\lfloor \epsilon (n/\tilde{k}) \log\!(n) \rfloor$
where
![]() $0\lt \varepsilon \lt 1$
, we have
$0\lt \varepsilon \lt 1$
, we have
where the second inequality holds by (1) and the last since
![]() $\tilde{k}\geq n^{\gamma }$
where
$\tilde{k}\geq n^{\gamma }$
where
![]() $\gamma \gt 0$
fixed.
$\gamma \gt 0$
fixed.
Finally, since each of these
![]() $\tilde{k}$
random walks can change
$\tilde{k}$
random walks can change
![]() $Z$
by at most
$Z$
by at most
![]() $\ell$
vertices, by the method of bounded differences [Reference Dubhashi and Panconesi18, Theorem 5.3],
$\ell$
vertices, by the method of bounded differences [Reference Dubhashi and Panconesi18, Theorem 5.3],
 \begin{equation*}{\mathbb{P}}\left [Z\lt {\mathbb{E}} \left [Z\right ]/2\right ]\leq \exp\!\left (-2\frac {(Z/2 )^2 }{\tilde {k}\ell ^2 } \right ) \leq \exp\!\left (- \frac { n^{2-18\epsilon } \tilde {k} }{8 \varepsilon ^2 n^2 \log ^2 n } \right ) \lt 1/2, \end{equation*}
\begin{equation*}{\mathbb{P}}\left [Z\lt {\mathbb{E}} \left [Z\right ]/2\right ]\leq \exp\!\left (-2\frac {(Z/2 )^2 }{\tilde {k}\ell ^2 } \right ) \leq \exp\!\left (- \frac { n^{2-18\epsilon } \tilde {k} }{8 \varepsilon ^2 n^2 \log ^2 n } \right ) \lt 1/2, \end{equation*}
provided we have
![]() $\epsilon \lt \gamma/18$
as
$\epsilon \lt \gamma/18$
as
![]() $\tilde{k} \geq n^{\gamma }$
. This implies that
$\tilde{k} \geq n^{\gamma }$
. This implies that
![]() ${\mathbb{P}} [Z \geq 1] \geq 1/2$
.
${\mathbb{P}} [Z \geq 1] \geq 1/2$
.
Proof of Theorem
4.9. Since we are bounding the worst-case cover time from below we can assume that all walks start from a single vertex
![]() $u$
. First, consider the
$u$
. First, consider the
![]() $k$
walks running for
$k$
walks running for
![]() $ t_{\mathsf{large-hit}}^{(\tilde{k},k)} -1$
steps. Then, by the definition of
$ t_{\mathsf{large-hit}}^{(\tilde{k},k)} -1$
steps. Then, by the definition of
![]() $ t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
, there exists a vertex
$ t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
, there exists a vertex
![]() $u$
and
$u$
and
![]() $S\subseteq V$
such that
$S\subseteq V$
such that
![]() ${\mathbb{P}}_{u}[\tau _{S}\leq t ] \lt \tilde k/k$
, therefore, the number of walks that, starting from
${\mathbb{P}}_{u}[\tau _{S}\leq t ] \lt \tilde k/k$
, therefore, the number of walks that, starting from
![]() $u$
, hit
$u$
, hit
![]() $S$
before time
$S$
before time
![]() $t$
is dominated by a binomial distribution with parameters
$t$
is dominated by a binomial distribution with parameters
![]() $k$
and
$k$
and
![]() $p = \tilde k/k$
, whose expected value and median is
$p = \tilde k/k$
, whose expected value and median is
![]() $\tilde k$
. We conclude that, if
$\tilde k$
. We conclude that, if
![]() $\mathcal{E}$
is the event that at most
$\mathcal{E}$
is the event that at most
![]() $\tilde k$
walks hit
$\tilde k$
walks hit
![]() $S$
by time
$S$
by time
![]() $ t_{\mathsf{large-hit}}^{(\tilde{k},k)}-1$
, then
$ t_{\mathsf{large-hit}}^{(\tilde{k},k)}-1$
, then
![]() ${\mathbb{P}} [\mathcal{E}]\geq 1/2$
.
${\mathbb{P}} [\mathcal{E}]\geq 1/2$
.
Although, conditional on
![]() $\mathcal{E}$
, we know at most
$\mathcal{E}$
, we know at most
![]() $\tilde{k}$
walks hit
$\tilde{k}$
walks hit
![]() $S$
by time
$S$
by time
![]() $ t_{\mathsf{large-hit}}^{(\tilde{k},k)} -1$
, we do not know when they arrived or which vertices of
$ t_{\mathsf{large-hit}}^{(\tilde{k},k)} -1$
, we do not know when they arrived or which vertices of
![]() $S$
they hit first. For a lower bound we assume these
$S$
they hit first. For a lower bound we assume these
![]() $\tilde{k}$
walks arrived at time
$\tilde{k}$
walks arrived at time
![]() $0$
and then take the minimum over all sets
$0$
and then take the minimum over all sets
![]() $S$
such that
$S$
such that
![]() $\pi (S)\geq 1/4$
and starting distributions
$\pi (S)\geq 1/4$
and starting distributions
![]() $\mu$
on
$\mu$
on
![]() $\partial S$
, the vertex boundary of
$\partial S$
, the vertex boundary of
![]() $S$
(note all particles started from
$S$
(note all particles started from
![]() $u$
, so they have the same distribution when they enter
$u$
, so they have the same distribution when they enter
![]() $S$
for first time). It follows that, conditional on
$S$
for first time). It follows that, conditional on
![]() $\mathcal{E}$
, the expected time for
$\mathcal{E}$
, the expected time for
![]() $\tilde{k}$
walks which hit
$\tilde{k}$
walks which hit
![]() $S$
before time
$S$
before time
![]() $ t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
to cover
$ t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
to cover
![]() $S$
is at least
$S$
is at least
![]() $t_{\mathsf{large-cov}}^{(\tilde k)}$
and so the result follows.
$t_{\mathsf{large-cov}}^{(\tilde k)}$
and so the result follows.
4.6. Proofs of bounds on the large-hit and large-cover times
Proof of Lemma
4.10. Let
![]() $S \subseteq V$
be a set such that
$S \subseteq V$
be a set such that
![]() $\Phi (G)=\Phi (S)$
and
$\Phi (G)=\Phi (S)$
and
![]() $\pi (V \setminus S) \geq 1/2$
(such a set exists by symmetry of
$\pi (V \setminus S) \geq 1/2$
(such a set exists by symmetry of
![]() $\Phi (S)=\Phi (V \setminus S)$
). Let
$\Phi (S)=\Phi (V \setminus S)$
). Let
![]() $\pi _{S}$
be the stationary distribution restricted to
$\pi _{S}$
be the stationary distribution restricted to
![]() $S$
, that is
$S$
, that is
![]() $\pi _{S}(s)= \pi (s)/\pi (S)$
for
$\pi _{S}(s)= \pi (s)/\pi (S)$
for
![]() $s\in S$
and
$s\in S$
and
![]() $\pi _{S}(x)=0$
for
$\pi _{S}(x)=0$
for
![]() $x\notin S$
. As shown in [Reference Gharan and Trevisan24, Proposition 8], the probability that a (single) random walk
$x\notin S$
. As shown in [Reference Gharan and Trevisan24, Proposition 8], the probability that a (single) random walk
![]() $X_t$
remains in a set
$X_t$
remains in a set
![]() $S$
when starting from a vertex in
$S$
when starting from a vertex in
![]() $S$
sampled from
$S$
sampled from
![]() $\pi _{S}$
, within
$\pi _{S}$
, within
![]() $t$
steps is at least
$t$
steps is at least
![]() $ (1-\Phi (S)/2)^{t} \geq 1 - \Phi (S) t/2$
. Let
$ (1-\Phi (S)/2)^{t} \geq 1 - \Phi (S) t/2$
. Let
![]() $t\lt \frac{2\tilde k}{k\Phi (S)}$
, then
$t\lt \frac{2\tilde k}{k\Phi (S)}$
, then
![]() ${\mathbb{P}}_{\pi _S}[\tau _{S^c} \leq t ] \lt \tilde k/k$
, and thus by taking
${\mathbb{P}}_{\pi _S}[\tau _{S^c} \leq t ] \lt \tilde k/k$
, and thus by taking
![]() $u$
as the vertex that minimises the escape probability from
$u$
as the vertex that minimises the escape probability from
![]() $S$
, we conclude that
$S$
, we conclude that
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)} \geq \frac{\tilde{k}}{k} \cdot \frac{2}{\Phi (S)}$
.
$t_{\mathsf{large-hit}}^{(\tilde{k},k)} \geq \frac{\tilde{k}}{k} \cdot \frac{2}{\Phi (S)}$
.
Before proving Lemma 4.11 we first establish an elementary result.
Lemma 4.13. (cf. [Reference Lyons and Peres47], Theorem 13.4). Let
![]() $G=(V,E)$
be a
$G=(V,E)$
be a
![]() $d$
-dimensional torus (
$d$
-dimensional torus (
![]() $d \geq 2$
) or cycle (
$d \geq 2$
) or cycle (
![]() $d=1$
). Then for any
$d=1$
). Then for any
![]() $ D\geq 0$
and
$ D\geq 0$
and
![]() $t \geq 1$
,
$t \geq 1$
,
Proof of Lemma
4.13. Consider a random walk for
![]() $t$
steps on a
$t$
steps on a
![]() $d$
-dimensional torus (or cycle), where
$d$
-dimensional torus (or cycle), where
![]() $d\geq 1$
. Let
$d\geq 1$
. Let
![]() $Z_1,Z_2,\ldots,Z_{t} \in \{-1,0,+1\}$
be the transitions along the first dimension, and let
$Z_1,Z_2,\ldots,Z_{t} \in \{-1,0,+1\}$
be the transitions along the first dimension, and let
![]() $S_i = Z_1+\ldots + Z_i$
. Note that
$S_i = Z_1+\ldots + Z_i$
. Note that
![]() $S_i$
is a zero-mean martingale with respect to the
$S_i$
is a zero-mean martingale with respect to the
![]() $Z_i$
. Define
$Z_i$
. Define
![]() $\tau =\min \{i\;:\; |S_i|\geq D/d\}\wedge t$
, which is a bounded stopping time, and thus
$\tau =\min \{i\;:\; |S_i|\geq D/d\}\wedge t$
, which is a bounded stopping time, and thus
![]() $S_{\tau \wedge i}$
is another martingale with increments bounded by 1. Then, by Azuma’s inequality [Reference Mitzenmacher and Upfal49, Theorem 13.4],
$S_{\tau \wedge i}$
is another martingale with increments bounded by 1. Then, by Azuma’s inequality [Reference Mitzenmacher and Upfal49, Theorem 13.4],
Now, for the random walk, in order to overcome a distance
![]() $D$
during
$D$
during
![]() $t$
steps, the above event must occur for at least one of the
$t$
steps, the above event must occur for at least one of the
![]() $d$
dimensions, so by the union bound
$d$
dimensions, so by the union bound
as claimed.
Proof of Lemma
4.11. Recall from the definition of
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
that there must exist a vertex
$t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
that there must exist a vertex
![]() $u$
and set
$u$
and set
![]() $S$
with
$S$
with
![]() $\pi (S)\geq 1/4$
such that the probability a random walk of length
$\pi (S)\geq 1/4$
such that the probability a random walk of length
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
started from
$t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
started from
![]() $u$
has hit
$u$
has hit
![]() $S$
is at most
$S$
is at most
![]() $\tilde k/ k$
. Notice that since the
$\tilde k/ k$
. Notice that since the
![]() $d$
-dimensional torus is regular any set
$d$
-dimensional torus is regular any set
![]() $S$
of size at least
$S$
of size at least
![]() $n/4$
satisfies
$n/4$
satisfies
![]() $\pi (S)\geq 1/4$
. In order for a random walk to hit the set
$\pi (S)\geq 1/4$
. In order for a random walk to hit the set
![]() $S$
within
$S$
within
![]() $t$
steps, it must reach a distance
$t$
steps, it must reach a distance
![]() $D=\textrm{dist}(u,S)$
from
$D=\textrm{dist}(u,S)$
from
![]() $u$
at least once during
$u$
at least once during
![]() $t$
steps. Let
$t$
steps. Let
![]() $t$
be given by
$t$
be given by
 \begin{equation*}t = \left \lfloor \frac {D^2}{2d^2\log \left (2dk/\tilde k\right )}\right \rfloor .\end{equation*}
\begin{equation*}t = \left \lfloor \frac {D^2}{2d^2\log \left (2dk/\tilde k\right )}\right \rfloor .\end{equation*}
Then by Lemma 4.13,
and the result follows.
Proof of Lemma
4.12. In the first part of the proof we will work with random walks whose lengths are independent samples from
![]() $\operatorname{Geo}(1/t )$
. That is, we consider walks
$\operatorname{Geo}(1/t )$
. That is, we consider walks
![]() $(X_0,X_1,\ldots, X_{L-1})$
where
$(X_0,X_1,\ldots, X_{L-1})$
where
![]() $L\geq 1$
is a geometric random variable with mean
$L\geq 1$
is a geometric random variable with mean
![]() $t$
, which is independent of the trajectory
$t$
, which is independent of the trajectory
![]() $(X_s)_{s\geq 0 }$
. Let
$(X_s)_{s\geq 0 }$
. Let
![]() $\tilde P_{w,u}^s = {\mathbb{P}}_{w}[X_s = u, s\lt L ]$
. We call the above a geometric random walk of expected length
$\tilde P_{w,u}^s = {\mathbb{P}}_{w}[X_s = u, s\lt L ]$
. We call the above a geometric random walk of expected length
![]() $t$
. We consider a collection of
$t$
. We consider a collection of
![]() $k$
independent geometric random walks of length
$k$
independent geometric random walks of length
![]() $t$
, in particular the lengths of these walks are also independent of each other.
$t$
, in particular the lengths of these walks are also independent of each other.
Let us lower bound the expected number of unvisited vertices in
![]() $S$
by
$S$
by
![]() $k$
independent geometric random walks of expected length
$k$
independent geometric random walks of expected length
![]() $t$
. Define a subset
$t$
. Define a subset
![]() $S' \subseteq S$
as
$S' \subseteq S$
as
 \begin{equation*} S' = \left \{ u \in S \;\colon \sum _{s=0}^{\infty } \sum _{w \in V} \mu (w) \tilde {P}_{w,u}^s \leq 8 t \cdot \pi (u) \right \}. \end{equation*}
\begin{equation*} S' = \left \{ u \in S \;\colon \sum _{s=0}^{\infty } \sum _{w \in V} \mu (w) \tilde {P}_{w,u}^s \leq 8 t \cdot \pi (u) \right \}. \end{equation*}
Since the geometric random walk has an expected length of
![]() $t$
, it visits at most
$t$
, it visits at most
![]() $t$
vertices in expectation and thus
$t$
vertices in expectation and thus
It follows by definition of
![]() $S'$
that
$S'$
that
 \begin{equation*} t \geq \sum _{u \in V \setminus S'} \sum _{s=0}^{\infty } \sum _{w \in V} \mu (w) \tilde {P}_{w,u}^s \geq \sum _{u \in V \setminus S'} 8 t \cdot \pi (u), \end{equation*}
\begin{equation*} t \geq \sum _{u \in V \setminus S'} \sum _{s=0}^{\infty } \sum _{w \in V} \mu (w) \tilde {P}_{w,u}^s \geq \sum _{u \in V \setminus S'} 8 t \cdot \pi (u), \end{equation*}
and thus
![]() $\sum _{u \in V \setminus S'} \pi (u) \leq 1/8$
. Hence
$\sum _{u \in V \setminus S'} \pi (u) \leq 1/8$
. Hence
![]() $\sum _{u \in S'} \pi (u) \geq \pi (S)-1/8 \geq 1/4-1/8 = 1/8$
.
$\sum _{u \in S'} \pi (u) \geq \pi (S)-1/8 \geq 1/4-1/8 = 1/8$
.
Let
![]() $Z_t=Z_t(u)$
denote the number of visits to
$Z_t=Z_t(u)$
denote the number of visits to
![]() $u$
by a geometric random walk of expected length
$u$
by a geometric random walk of expected length
![]() $t$
. The probability a single walk starting from
$t$
. The probability a single walk starting from
![]() $\mu$
visits a vertex
$\mu$
visits a vertex
![]() $u \in S'$
before being killed is at most
$u \in S'$
before being killed is at most
since conditional on the walk having reached a vertex
![]() $u$
, the expected remaining returns before getting killed is equal to
$u$
, the expected remaining returns before getting killed is equal to
![]() $\sum _{s=0}^{\infty } \tilde{P}_{u,u}^s$
. Now observe that
$\sum _{s=0}^{\infty } \tilde{P}_{u,u}^s$
. Now observe that
![]() $\tilde{P}^{s}_{u,u} \geq \frac{1}{4} \cdot P_{u,u}^{s}$
, which follows since
$\tilde{P}^{s}_{u,u} \geq \frac{1}{4} \cdot P_{u,u}^{s}$
, which follows since
![]() ${\mathbb{P}}\left [ \operatorname{Geo}\!\left (1/t\right ) \gt s\right ] = \left (1 - \frac{1}{t} \right )^{s} \geq \left (1 - \frac{1}{t} \right )^{t}\geq 1/4$
, for any
${\mathbb{P}}\left [ \operatorname{Geo}\!\left (1/t\right ) \gt s\right ] = \left (1 - \frac{1}{t} \right )^{s} \geq \left (1 - \frac{1}{t} \right )^{t}\geq 1/4$
, for any
![]() $t\geq 2$
and any
$t\geq 2$
and any
![]() $s\leq t$
. Thus we have
$s\leq t$
. Thus we have
 \begin{align*} {\mathbb{P}}_{\mu }\!\left [ Z_t \geq 1\right ] &\leq \frac{ \sum _{s=0}^{\infty } \sum _{w \in V} \mu (w) \tilde{P}_{w,u}^s }{ \frac{1}{4}\cdot \sum _{s=0}^{t} P_{u,u}^s } \leq \frac{8 t \cdot \pi (u)}{\frac{1}{4} \cdot ( 32 \cdot t\cdot \pi (u) \cdot k)} =\frac{1}{k}, \end{align*}
\begin{align*} {\mathbb{P}}_{\mu }\!\left [ Z_t \geq 1\right ] &\leq \frac{ \sum _{s=0}^{\infty } \sum _{w \in V} \mu (w) \tilde{P}_{w,u}^s }{ \frac{1}{4}\cdot \sum _{s=0}^{t} P_{u,u}^s } \leq \frac{8 t \cdot \pi (u)}{\frac{1}{4} \cdot ( 32 \cdot t\cdot \pi (u) \cdot k)} =\frac{1}{k}, \end{align*}
by hypothesis. Let
![]() $Y$
the stationary mass of the unvisited vertices in
$Y$
the stationary mass of the unvisited vertices in
![]() $S'$
, then
$S'$
, then
 \begin{equation*} {\mathbb{E}} \left [ Y \right ] \geq \sum _{u \in S'} \pi (u) \cdot \left (1 - \frac {1}{k} \right )^{k} \geq \frac {1}{4} \cdot \pi (S'). \end{equation*}
\begin{equation*} {\mathbb{E}} \left [ Y \right ] \geq \sum _{u \in S'} \pi (u) \cdot \left (1 - \frac {1}{k} \right )^{k} \geq \frac {1}{4} \cdot \pi (S'). \end{equation*}
Hence with probability at least
![]() $1/4$
, at least one vertex in
$1/4$
, at least one vertex in
![]() $S'$
remains unvisited by the
$S'$
remains unvisited by the
![]() $k$
random walks whose length is sampled from
$k$
random walks whose length is sampled from
![]() $\operatorname{Geo}(1/t )$
. Finally, since each walk is independent the number of walks which run for more than
$\operatorname{Geo}(1/t )$
. Finally, since each walk is independent the number of walks which run for more than
![]() $t$
steps is binomially distributed with parameters
$t$
steps is binomially distributed with parameters
![]() $k$
and
$k$
and
![]() $p= (1 - 1/t)^t \geq 1/4$
. Thus by a Chernoff bound the probability that less than
$p= (1 - 1/t)^t \geq 1/4$
. Thus by a Chernoff bound the probability that less than
![]() $1/8$
of the
$1/8$
of the
![]() $k$
random walks run for more than
$k$
random walks run for more than
![]() $t$
steps is at most
$t$
steps is at most
![]() $\exp\!\left (-\frac{(k/8)^2}{(2k/4)} \right )= e^{-k/32}$
. Hence, by coupling,
$\exp\!\left (-\frac{(k/8)^2}{(2k/4)} \right )= e^{-k/32}$
. Hence, by coupling,
![]() $k/8$
random walks of length
$k/8$
random walks of length
![]() $t$
do not visit all vertices in
$t$
do not visit all vertices in
![]() $S'$
with probability at least
$S'$
with probability at least
![]() $1/4-e^{-k/32} \geq 1/5$
, provided
$1/4-e^{-k/32} \geq 1/5$
, provided
![]() $k\geq 100$
.
$k\geq 100$
.
5. Applications to standard graphs
In this section, we apply the results of the previous sections to determine the stationary and worst-case multiple walk cover times. Firstly, we determine the stationary cover times for many fundamental networks using results from Sections 3 and 4. Secondly, using our results for the stationary cover times, we then apply them to the
![]() $\min$
-
$\min$
-
![]() $\max$
(and
$\max$
(and
![]() $\max$
-
$\max$
-
![]() $\min$
) characterisations from Section 4. Along the way, we also have to derive bounds for the partial mixing time and the time to hit a large set. Due to this section being large, the proofs of all results are located in the same subsections as the statements (unlike Sections 3 and 4). For a quick reference and comparison of the results of this section the reader is encouraged to consult Table 1.
$\min$
) characterisations from Section 4. Along the way, we also have to derive bounds for the partial mixing time and the time to hit a large set. Due to this section being large, the proofs of all results are located in the same subsections as the statements (unlike Sections 3 and 4). For a quick reference and comparison of the results of this section the reader is encouraged to consult Table 1.
5.1. The cycle
Our first result determines the stationary cover time of the cycle up to constants. This result comes from Theorem 3.1 and Lemma 3.9 along with some additional results and arguments.
Theorem 5.1.
For the
![]() $n$
-vertex cycle
$n$
-vertex cycle
![]() $C_n$
, and any integer
$C_n$
, and any integer
![]() $ k \geq 2$
, we have
$ k \geq 2$
, we have
The lower bound for
![]() $t_{\mathsf{cov}}^{(k)}(\pi )$
provided
$t_{\mathsf{cov}}^{(k)}(\pi )$
provided
![]() $k\geq n^{1/20}$
was already known [Reference Klasing, Kosowski, Pajak, Sauerwald, Fatourou and Taubenfeld37, Lemma 18]. Here, we prove Theorem 5.1, which holds for any
$k\geq n^{1/20}$
was already known [Reference Klasing, Kosowski, Pajak, Sauerwald, Fatourou and Taubenfeld37, Lemma 18]. Here, we prove Theorem 5.1, which holds for any
![]() $k\geq 2$
, by extending the applicable range of
$k\geq 2$
, by extending the applicable range of
![]() $k$
for the lower bound and supplying a new upper bound. We also demonstrate how to fully recover the worst-case cover time below using our new methods from Section 4.
$k$
for the lower bound and supplying a new upper bound. We also demonstrate how to fully recover the worst-case cover time below using our new methods from Section 4.
Theorem 5.2. ([Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5], Theorem 3.4). For the
![]() $n$
-vertex cycle
$n$
-vertex cycle
![]() $C_n$
, and any
$C_n$
, and any
![]() $2 \leq k \leq n$
, we have
$2 \leq k \leq n$
, we have
We begin with the proof for the stationary case.
Proof of Theorem
5.1. We split the analysis for
![]() $k\geq 2$
into two cases.
$k\geq 2$
into two cases.
Case (i) [
![]() $2\lt k\leq n^{1/20}$
]: The lower bound is covered by [Reference Klasing, Kosowski, Pajak, Sauerwald, Fatourou and Taubenfeld37, Lemma 18] so we just prove the upper bound. For a single walk
$2\lt k\leq n^{1/20}$
]: The lower bound is covered by [Reference Klasing, Kosowski, Pajak, Sauerwald, Fatourou and Taubenfeld37, Lemma 18] so we just prove the upper bound. For a single walk
![]() $t_{\mathsf{cov}}(\pi ) = \mathcal{O}(n^2)$
[Reference Aldous and Fill2, Proposition 6.7] and so since
$t_{\mathsf{cov}}(\pi ) = \mathcal{O}(n^2)$
[Reference Aldous and Fill2, Proposition 6.7] and so since
![]() $k$
walks take at most as long to cover as a single walk, we can assume that
$k$
walks take at most as long to cover as a single walk, we can assume that
![]() $k\geq 10000$
when proving the upper bound.
$k\geq 10000$
when proving the upper bound.
To begin, divide the cycle as evenly as possible into
![]() $k$
disjoint intervals
$k$
disjoint intervals
![]() $\mathcal{I}_1,\dots, \mathcal{I}_k$
of consecutive vertices, each of size
$\mathcal{I}_1,\dots, \mathcal{I}_k$
of consecutive vertices, each of size
![]() $\lfloor n/k\rfloor$
or
$\lfloor n/k\rfloor$
or
![]() $\lceil n/k\rceil$
. For
$\lceil n/k\rceil$
. For
![]() $2 \leq c \leq k/\log k$
let
$2 \leq c \leq k/\log k$
let
![]() $t^*(c)=t^* = \lceil (cn/k)^2\log ^2 k\rceil$
. Now, for each interval
$t^*(c)=t^* = \lceil (cn/k)^2\log ^2 k\rceil$
. Now, for each interval
![]() $\mathcal{I}_i$
we let
$\mathcal{I}_i$
we let
![]() $\mathcal{J}_i(c)$
be an interval of length
$\mathcal{J}_i(c)$
be an interval of length
![]() $\ell =\lfloor \sqrt{t^*(c)} \rfloor \leq n$
centred around
$\ell =\lfloor \sqrt{t^*(c)} \rfloor \leq n$
centred around
![]() $\mathcal{I}_i$
. Note that since
$\mathcal{I}_i$
. Note that since
![]() $c\geq 2$
and
$c\geq 2$
and
![]() $n$
is large we have
$n$
is large we have
![]() $\mathcal{I}_i\subset \mathcal{J}_i$
for each
$\mathcal{I}_i\subset \mathcal{J}_i$
for each
![]() $1\leq i\leq k$
.
$1\leq i\leq k$
.
Claim 5.3.
For any
![]() $2 \leq c \leq k/\log k$
, a walk of length
$2 \leq c \leq k/\log k$
, a walk of length
![]() $t^*(c)$
starting at any vertex in the interval
$t^*(c)$
starting at any vertex in the interval
![]() $\mathcal{J}_i(c)$
will visit all vertices of
$\mathcal{J}_i(c)$
will visit all vertices of
![]() $\mathcal{I}_i$
with probability at least
$\mathcal{I}_i$
with probability at least
![]() $1/250$
when
$1/250$
when
![]() $n$
is suitably large.
$n$
is suitably large.
Proof of Claim
5.3. Let
![]() $\mathcal{N}(0,1)$
be the standard normal distribution, then by [Reference Gordon26] for any
$\mathcal{N}(0,1)$
be the standard normal distribution, then by [Reference Gordon26] for any
![]() $x\gt 0$
:
$x\gt 0$
:
Note that all vertices of
![]() $\mathcal I_i$
will have been covered if the walk has travelled from one endpoint of
$\mathcal I_i$
will have been covered if the walk has travelled from one endpoint of
![]() $\mathcal J_i$
to the other via a path contained within
$\mathcal J_i$
to the other via a path contained within
![]() $\mathcal J_i$
. Let
$\mathcal J_i$
. Let
![]() $S_j$
be the distance of a random walk at time
$S_j$
be the distance of a random walk at time
![]() $j$
from its start point. Then, for large
$j$
from its start point. Then, for large
![]() $n$
, by the Central Limit Theorem and (18) we have
$n$
, by the Central Limit Theorem and (18) we have
Now, by symmetry and (19), regardless of its start point within the interval
![]() $\mathcal J_i$
, with probability at least
$\mathcal J_i$
, with probability at least
![]() $1/15$
the walk will have hit the ‘left’ end of
$1/15$
the walk will have hit the ‘left’ end of
![]() $\mathcal J_i$
within at most
$\mathcal J_i$
within at most
![]() $t^*/2$
steps. Once at the ‘left’ end of
$t^*/2$
steps. Once at the ‘left’ end of
![]() $\mathcal J_i$
, then again by (19) with probability at least
$\mathcal J_i$
, then again by (19) with probability at least
![]() $1/15$
, it will have reached the right end via a path though
$1/15$
, it will have reached the right end via a path though
![]() $\mathcal J_i$
within at most
$\mathcal J_i$
within at most
![]() $t^*/2$
additional steps. Thus, for suitably large
$t^*/2$
additional steps. Thus, for suitably large
![]() $n$
, with probability at least
$n$
, with probability at least
![]() $(1/15)^2 \gt 1/250$
a walk of length
$(1/15)^2 \gt 1/250$
a walk of length
![]() $t^*$
starting in
$t^*$
starting in
![]() $\mathcal J_i$
will cover
$\mathcal J_i$
will cover
![]() $\mathcal I_i$
.
$\mathcal I_i$
.
Let
![]() $w_i$
be the number of walks which start in
$w_i$
be the number of walks which start in
![]() $\mathcal{J}_i$
. By Chernoff’s bound [Reference Mitzenmacher and Upfal49, Theorem 4.5]:
$\mathcal{J}_i$
. By Chernoff’s bound [Reference Mitzenmacher and Upfal49, Theorem 4.5]:
By Claim 5.3, conditional on
![]() $w_i$
, none of the walks in
$w_i$
, none of the walks in
![]() $\mathcal{J}_i$
cover
$\mathcal{J}_i$
cover
![]() $\mathcal{I}_i$
w.p. at most
$\mathcal{I}_i$
w.p. at most
![]() $\left(\frac{249}{250}\right)^{w_i}$
when
$\left(\frac{249}{250}\right)^{w_i}$
when
![]() $n$
is large. Hence, by (20) a fixed interval
$n$
is large. Hence, by (20) a fixed interval
![]() $\mathcal{I}_i$
is not covered w.p. at most
$\mathcal{I}_i$
is not covered w.p. at most
![]() $(249/250)^{(3/4)\cdot c\log k} + k^{-c/32}$
. As
$(249/250)^{(3/4)\cdot c\log k} + k^{-c/32}$
. As
![]() $(3/4)\ln (249/250)\lt -3/1000$
and
$(3/4)\ln (249/250)\lt -3/1000$
and
![]() $k\geq 10000$
, for any
$k\geq 10000$
, for any
![]() $1000\leq c \leq k/\log k$
, we have
$1000\leq c \leq k/\log k$
, we have
by the union bound. Now, as
![]() $t^*(k/\log k) = n^2$
, observe that we have
$t^*(k/\log k) = n^2$
, observe that we have
 \begin{equation} {\mathbb{E}}_{\pi ^k} \left [\tau _{\mathsf{cov}}^{(k)} \right ] \leq t^*(1000) +\sum _{i=1000}^{\lfloor \frac{k}{\log k }\rfloor } [t^*(i+1)-t^*(i)]\cdot {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt t^*(i)\right ] + \sum _{t=n^2}^\infty {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt t\right ]. \end{equation}
\begin{equation} {\mathbb{E}}_{\pi ^k} \left [\tau _{\mathsf{cov}}^{(k)} \right ] \leq t^*(1000) +\sum _{i=1000}^{\lfloor \frac{k}{\log k }\rfloor } [t^*(i+1)-t^*(i)]\cdot {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt t^*(i)\right ] + \sum _{t=n^2}^\infty {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt t\right ]. \end{equation}
Using
![]() ${\mathbb{P}}_{\pi ^k}[\tau _{\mathsf{cov}}^{(k)}\gt t^*(i) ] \leq k^{-i/1000}$
for
${\mathbb{P}}_{\pi ^k}[\tau _{\mathsf{cov}}^{(k)}\gt t^*(i) ] \leq k^{-i/1000}$
for
![]() $1000\leq i \leq k/\log k$
by (21), gives
$1000\leq i \leq k/\log k$
by (21), gives
 \begin{equation} \begin{aligned}\sum _{i=1000}^{\frac{k}{\log k }} [t^*(i+1)-t^*(i)]\cdot {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt t^*(i)\right ] &\leq \left (\left (\frac{n}{k}\right )^2\log ^2 k + 1 \right ) \sum _{i=0}^{\infty } (2i+1) \cdot k^{-i/1000} \\[5pt] &= \mathcal{O}\!\left (\left (\frac{n}{k}\right )^2\log ^2 k\right ).\end{aligned} \end{equation}
\begin{equation} \begin{aligned}\sum _{i=1000}^{\frac{k}{\log k }} [t^*(i+1)-t^*(i)]\cdot {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt t^*(i)\right ] &\leq \left (\left (\frac{n}{k}\right )^2\log ^2 k + 1 \right ) \sum _{i=0}^{\infty } (2i+1) \cdot k^{-i/1000} \\[5pt] &= \mathcal{O}\!\left (\left (\frac{n}{k}\right )^2\log ^2 k\right ).\end{aligned} \end{equation}
Recall that
![]() ${\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt t^*(k/\log k) \right ] \leq k^{- \frac{1}{1000}\cdot k/\log k}=e^{-k/1000}$
by (21). If
${\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt t^*(k/\log k) \right ] \leq k^{- \frac{1}{1000}\cdot k/\log k}=e^{-k/1000}$
by (21). If
![]() $\textbf{v}$
is the worst-case start position vector for
$\textbf{v}$
is the worst-case start position vector for
![]() $k$
walks to cover a cycle then for any
$k$
walks to cover a cycle then for any
![]() $t= i\cdot n^2$
and
$t= i\cdot n^2$
and
![]() $i\geq 1$
,
$i\geq 1$
,
by the Markov property. Note that
![]() ${\mathbb{P}}_{\textbf{v}}[\tau _{\mathsf{cov}}^{(k)}\gt (i-1)n^2 ]\leq (1/2)^{i-1}$
by Markov’s inequality since
${\mathbb{P}}_{\textbf{v}}[\tau _{\mathsf{cov}}^{(k)}\gt (i-1)n^2 ]\leq (1/2)^{i-1}$
by Markov’s inequality since
![]() $t_{\mathsf{cov}} = n(n-1)/2$
. Thus the second sum on the RHS of (22) satisfies
$t_{\mathsf{cov}} = n(n-1)/2$
. Thus the second sum on the RHS of (22) satisfies
 \begin{equation} \sum _{t=n^2}^\infty {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt t\right ] \leq n^2\cdot \sum _{i=1}^\infty {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt i\cdot n^2\right ] \leq n^2\cdot \sum _{i=1}^\infty e^{-k/1000}2^{-i+1} = 2e^{-k/1000}n^2 . \end{equation}
\begin{equation} \sum _{t=n^2}^\infty {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt t\right ] \leq n^2\cdot \sum _{i=1}^\infty {\mathbb{P}}_{\pi ^k}\!\left [\tau _{\mathsf{cov}}^{(k)}\gt i\cdot n^2\right ] \leq n^2\cdot \sum _{i=1}^\infty e^{-k/1000}2^{-i+1} = 2e^{-k/1000}n^2 . \end{equation}
Case (
![]() $i$
) then follows by inserting (23) and (24) into (22).
$i$
) then follows by inserting (23) and (24) into (22).
Case (ii) [
![]() $k\gt n^{1/20}$
]: The upper bound follows from Theorem 3.1 since in this case
$k\gt n^{1/20}$
]: The upper bound follows from Theorem 3.1 since in this case
![]() $\log k=\Omega (\!\log n )$
. By Lemma A.2 we have
$\log k=\Omega (\!\log n )$
. By Lemma A.2 we have
![]() $\sum _{i=0}^{\lfloor t/2\rfloor }P_{v,v}^{2i} =\Omega (\sqrt{t} )$
so, by Lemma 3.10 (ii),
$\sum _{i=0}^{\lfloor t/2\rfloor }P_{v,v}^{2i} =\Omega (\sqrt{t} )$
so, by Lemma 3.10 (ii),
We shall now apply Lemma 3.9 with
![]() $S=V$
and so if we set
$S=V$
and so if we set
![]() $t= (cn/k)^2\log ^2 k$
for a suitably small constant
$t= (cn/k)^2\log ^2 k$
for a suitably small constant
![]() $c\gt 0$
then
$c\gt 0$
then
![]() $p=\max _{v\in S}{\mathbb{P}}_{\pi }\!\left [\tau _v\leq t\right ] \leq \frac{\log n}{100k},$
by (25). Observe that
$p=\max _{v\in S}{\mathbb{P}}_{\pi }\!\left [\tau _v\leq t\right ] \leq \frac{\log n}{100k},$
by (25). Observe that
![]() $|S|\min _{v\in S}\pi (v) = 1$
and also
$|S|\min _{v\in S}\pi (v) = 1$
and also
![]() $2p^2k \lt 1$
since
$2p^2k \lt 1$
since
![]() $k\geq n^{1/20}$
and
$k\geq n^{1/20}$
and
![]() $n$
is large. Thus Lemma 3.9 gives
$n$
is large. Thus Lemma 3.9 gives
as
![]() $k\geq n^{1/20}$
, which completes Case (
$k\geq n^{1/20}$
, which completes Case (
![]() $ii$
) and finishes the proof.
$ii$
) and finishes the proof.
The final element we need for our analysis is to identify the partial mixing time of the cycle. For such, we provide bounds for the partial mixing time for all
![]() $d$
-dimensional torus
$d$
-dimensional torus
![]() ${\mathbb{T}}_d$
(which are going to be used later), and we recall the cycle is the
${\mathbb{T}}_d$
(which are going to be used later), and we recall the cycle is the
![]() $1$
-dimensional torus
$1$
-dimensional torus
![]() ${\mathbb{T}}_1$
.
${\mathbb{T}}_1$
.
Lemma 5.4.
For any integer
![]() $d\geq 1$
there exists a constant
$d\geq 1$
there exists a constant
![]() $C_d\lt \infty$
such that for any
$C_d\lt \infty$
such that for any
![]() $1\leq \tilde{k} \leq k/2 = \mathcal{O}(n )$
the partial mixing time of the
$1\leq \tilde{k} \leq k/2 = \mathcal{O}(n )$
the partial mixing time of the
![]() $n$
-vertex torus
$n$
-vertex torus
![]() ${\mathbb{T}}_d$
satisfies
${\mathbb{T}}_d$
satisfies
![]() $t_{\mathsf{mix}}^{(\tilde k,k)} \leq C_d \cdot n^{2/d}/\log\!(k/\tilde{k}).$
$t_{\mathsf{mix}}^{(\tilde k,k)} \leq C_d \cdot n^{2/d}/\log\!(k/\tilde{k}).$
Proof. Let
![]() $Q$
and
$Q$
and
![]() $P$
be the transition matrices of the lazy walk on the (infinite)
$P$
be the transition matrices of the lazy walk on the (infinite)
![]() $d$
-dimensional integer lattice
$d$
-dimensional integer lattice
![]() $\mathbb{Z}^d$
and the (finite)
$\mathbb{Z}^d$
and the (finite)
![]() $d$
-dimensional
$d$
-dimensional
![]() $n$
-vertex torus
$n$
-vertex torus
![]() ${\mathbb{T}}_d$
, respectively. By [Reference Hebisch and Saloff-Coste28, Theorem 5.1 (15)], for each
${\mathbb{T}}_d$
, respectively. By [Reference Hebisch and Saloff-Coste28, Theorem 5.1 (15)], for each
![]() $d\geq 1$
there exist constants
$d\geq 1$
there exist constants
![]() $C,C',C''\gt 0$
such that for any
$C,C',C''\gt 0$
such that for any
![]() $t\geq 1$
and
$t\geq 1$
and
![]() $u,v \in \mathbb{Z}^d$
satisfying
$u,v \in \mathbb{Z}^d$
satisfying
![]() $||u -v||_{2} \leq t/C''$
we have
$||u -v||_{2} \leq t/C''$
we have
 \begin{equation} Q_{u,v}^t \geq \left (\frac{C}{t}\right )^{d/2}\exp\!\left (-C'\cdot \frac{ ||u-v||_2^2}{t} \right ) . \end{equation}
\begin{equation} Q_{u,v}^t \geq \left (\frac{C}{t}\right )^{d/2}\exp\!\left (-C'\cdot \frac{ ||u-v||_2^2}{t} \right ) . \end{equation}
For any
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $u,v\in V({\mathbb{T}}_d)$
we have
$u,v\in V({\mathbb{T}}_d)$
we have
![]() $ P_{u,v}^t \geq Q_{u,v}^t$
and
$ P_{u,v}^t \geq Q_{u,v}^t$
and
![]() $\| u - v \|_{\infty } \leq n^{1/d}/2$
. Therefore,
$\| u - v \|_{\infty } \leq n^{1/d}/2$
. Therefore,
and so if we set
 \begin{equation} t= \left \lceil \frac{ dC' \cdot n^{2/d}}{4\log\!(k/\tilde{k})}\right \rceil \leq \frac{dC'\cdot n^{2/d}}{2 \log\!(k/\tilde{k})}. \end{equation}
\begin{equation} t= \left \lceil \frac{ dC' \cdot n^{2/d}}{4\log\!(k/\tilde{k})}\right \rceil \leq \frac{dC'\cdot n^{2/d}}{2 \log\!(k/\tilde{k})}. \end{equation}
then, for large
![]() $n$
and any
$n$
and any
![]() $u,v \in V({\mathbb{T}}_d)$
, we have
$u,v \in V({\mathbb{T}}_d)$
, we have
![]() $||u -v||_{2} \leq t/C''$
and thus, by (26) and (27),
$||u -v||_{2} \leq t/C''$
and thus, by (26) and (27),
 \begin{equation*}P_{u,v}^t \geq \left (\frac {C}{t}\right )^{d/2}\cdot \exp\!\left (-C'\cdot \frac {dn^{2/d}/4}{t} \right ) \geq \frac {1}{n} \left (\frac {C2\log\!(k/\tilde {k})}{dC'}\right )^{d/2}\cdot \exp\!\left (- \log \left (\frac {k}{\tilde {k}}\right ) \right )\geq c'\cdot \frac {\tilde {k}}{n k} \end{equation*}
\begin{equation*}P_{u,v}^t \geq \left (\frac {C}{t}\right )^{d/2}\cdot \exp\!\left (-C'\cdot \frac {dn^{2/d}/4}{t} \right ) \geq \frac {1}{n} \left (\frac {C2\log\!(k/\tilde {k})}{dC'}\right )^{d/2}\cdot \exp\!\left (- \log \left (\frac {k}{\tilde {k}}\right ) \right )\geq c'\cdot \frac {\tilde {k}}{n k} \end{equation*}
for some
![]() $c'\;:\!=\; c'(d)$
, as
$c'\;:\!=\; c'(d)$
, as
![]() $ \log\!( k/\tilde{k}) \geq \log 2$
, which holds by hypothesis. It follows from the definition of separation distance that
$ \log\!( k/\tilde{k}) \geq \log 2$
, which holds by hypothesis. It follows from the definition of separation distance that
![]() $s(t)\leq 1 - c'\cdot \frac{\tilde{k}}{n k}$
for
$s(t)\leq 1 - c'\cdot \frac{\tilde{k}}{n k}$
for
![]() $t$
given by (28). Note that if
$t$
given by (28). Note that if
![]() $c'\geq 1$
then the statement of the lemma follows by (14), the definition of
$c'\geq 1$
then the statement of the lemma follows by (14), the definition of
![]() $t_{\mathsf{mix}}^{(\tilde k,k)}$
. Otherwise, assuming
$t_{\mathsf{mix}}^{(\tilde k,k)}$
. Otherwise, assuming
![]() $c' \lt 1$
, if we take
$c' \lt 1$
, if we take
![]() $t' = \lceil 2/c'\rceil \cdot t$
then as separation distance is sub-multiplicative [Reference Levin, Peres and Wilmer42, Ex. 6.4] we have
$t' = \lceil 2/c'\rceil \cdot t$
then as separation distance is sub-multiplicative [Reference Levin, Peres and Wilmer42, Ex. 6.4] we have
 \begin{equation*}s(t') \leq s(t)^{\left\lceil 2/c^{\prime}\right\rceil }\leq \left (1- \frac {c'\tilde {k}}{n k}\right )^{\lceil 2/c'\rceil }\leq \frac {1}{1 +\lceil 2/c'\rceil \cdot \frac {c'\tilde {k}}{n k} } = 1 - \frac { \lceil 2/c'\rceil \cdot \frac {c'\tilde {k}}{n k} }{1 +\lceil 2/c'\rceil \cdot \frac {c'\tilde {k}}{n k} }\leq 1- \frac {\tilde {k}}{n k}, \end{equation*}
\begin{equation*}s(t') \leq s(t)^{\left\lceil 2/c^{\prime}\right\rceil }\leq \left (1- \frac {c'\tilde {k}}{n k}\right )^{\lceil 2/c'\rceil }\leq \frac {1}{1 +\lceil 2/c'\rceil \cdot \frac {c'\tilde {k}}{n k} } = 1 - \frac { \lceil 2/c'\rceil \cdot \frac {c'\tilde {k}}{n k} }{1 +\lceil 2/c'\rceil \cdot \frac {c'\tilde {k}}{n k} }\leq 1- \frac {\tilde {k}}{n k}, \end{equation*}
for suitably large
![]() $n$
where in the second to last inequality we have used the fact that
$n$
where in the second to last inequality we have used the fact that
![]() $(1+x)^r \leq \frac{1}{1-rx}$
for any
$(1+x)^r \leq \frac{1}{1-rx}$
for any
![]() $r\geq 0$
and
$r\geq 0$
and
![]() $x\in [\!-\!1, 1/r)$
.
$x\in [\!-\!1, 1/r)$
.
Next we apply our new methodology to the cycle to recover the worst-case cover time from the stationary case.
Proof of Theorem
5.2. We can assume that
![]() $k\geq C$
for a large fixed constant
$k\geq C$
for a large fixed constant
![]() $C$
(in particular one satisfying
$C$
(in particular one satisfying
![]() $\log C \geq 1$
), as otherwise the result holds since
$\log C \geq 1$
), as otherwise the result holds since
![]() $t_{\mathsf{cov}} = \Theta (n^2)$
, and by [Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Theorem 4.2] the speed-up of the cover time on any graph is
$t_{\mathsf{cov}} = \Theta (n^2)$
, and by [Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Theorem 4.2] the speed-up of the cover time on any graph is
![]() $\mathcal{O}(k^2 )$
.
$\mathcal{O}(k^2 )$
.
For
![]() $k\geq C$
, define
$k\geq C$
, define
![]() $\tilde k = \lfloor \log\!(k) \rfloor \geq 1$
. Recall that
$\tilde k = \lfloor \log\!(k) \rfloor \geq 1$
. Recall that
![]() $t_{\mathsf{mix}}^{(\tilde k,k)} = \mathcal{O}(n^2/\log\!(k/\log k) ) = \mathcal{O}(n^2/\log k )$
by Lemma 5.4, and
$t_{\mathsf{mix}}^{(\tilde k,k)} = \mathcal{O}(n^2/\log\!(k/\log k) ) = \mathcal{O}(n^2/\log k )$
by Lemma 5.4, and
![]() $ t_{\mathsf{cov}}^{\tilde k}(\pi ) =\mathcal{O}\!\left (\frac{n^2}{(\!\log k)^2} (\!\log \log k)^2\right )$
by Theorem 5.1. Thus, Theorem 4.7 yields
$ t_{\mathsf{cov}}^{\tilde k}(\pi ) =\mathcal{O}\!\left (\frac{n^2}{(\!\log k)^2} (\!\log \log k)^2\right )$
by Theorem 5.1. Thus, Theorem 4.7 yields
![]() $t_{\mathsf{cov}}^{(k)}= \mathcal{O}\!\left ( \frac{n^2}{\log k}\right ).$
$t_{\mathsf{cov}}^{(k)}= \mathcal{O}\!\left ( \frac{n^2}{\log k}\right ).$
We will use Theorem 4.9 to prove the lower bound, and for such, we need lower bounds for
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
, and
$t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
, and
![]() $t_{\mathsf{large-cov}}^{(\tilde{k})}$
for an appropriate choice of
$t_{\mathsf{large-cov}}^{(\tilde{k})}$
for an appropriate choice of
![]() $\tilde k$
. We will indeed prove that if we choose
$\tilde k$
. We will indeed prove that if we choose
![]() $\tilde k$
as a constant, then
$\tilde k$
as a constant, then
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)} = \Omega ( n^2/\log k )$
and
$t_{\mathsf{large-hit}}^{(\tilde{k},k)} = \Omega ( n^2/\log k )$
and
![]() $t_{\mathsf{large-cov}}^{(\tilde{k})} = \Omega (n^2)$
, leading to the desired result as
$t_{\mathsf{large-cov}}^{(\tilde{k})} = \Omega (n^2)$
, leading to the desired result as
![]() $t_{\mathsf{cov}}^{(k)} = \Omega (\!\min (t_{\mathsf{large-hit}}^{(\tilde{k},k)},t_{\mathsf{large-cov}}^{(\tilde{k})}))$
.
$t_{\mathsf{cov}}^{(k)} = \Omega (\!\min (t_{\mathsf{large-hit}}^{(\tilde{k},k)},t_{\mathsf{large-cov}}^{(\tilde{k})}))$
.
For
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
we note that for any vertex
$t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
we note that for any vertex
![]() $u$
of the cycle we can find a set of vertices of size at least
$u$
of the cycle we can find a set of vertices of size at least
![]() $n/2$
with minimum distance at least
$n/2$
with minimum distance at least
![]() $ \lfloor n/4\rfloor$
from
$ \lfloor n/4\rfloor$
from
![]() $ u$
. Thus by Lemma 4.11 for any
$ u$
. Thus by Lemma 4.11 for any
![]() $\tilde{k} \leq k/2$
we have
$\tilde{k} \leq k/2$
we have
 \begin{equation*} t_{\mathsf {large-hit}}^{(\tilde {k},k)} = \Omega \left ( \frac {n^2}{\log\!( k/\tilde {k}) } \right ). \end{equation*}
\begin{equation*} t_{\mathsf {large-hit}}^{(\tilde {k},k)} = \Omega \left ( \frac {n^2}{\log\!( k/\tilde {k}) } \right ). \end{equation*}
To find a lower bound for
![]() $t_{\mathsf{large-cov}}^{(\tilde{k})}$
, by Lemma A.2 there exists some constant
$t_{\mathsf{large-cov}}^{(\tilde{k})}$
, by Lemma A.2 there exists some constant
![]() $c\gt 0$
such that for any
$c\gt 0$
such that for any
![]() $1\leq t\leq n^2$
and
$1\leq t\leq n^2$
and
![]() $u\in V$
the return probabilities in a cycle satisfy
$u\in V$
the return probabilities in a cycle satisfy
![]() $\sum _{s=0}^t P_{u,u}^{s} \geq c\sqrt{t}$
. Thus if we take
$\sum _{s=0}^t P_{u,u}^{s} \geq c\sqrt{t}$
. Thus if we take
![]() $\tilde{k} \geq \min (100,c/8)$
and let
$\tilde{k} \geq \min (100,c/8)$
and let
![]() $ t= \lfloor (cn/(256\tilde{k}) )^2 \rfloor$
then
$ t= \lfloor (cn/(256\tilde{k}) )^2 \rfloor$
then
![]() $c\sqrt{t}\geq 32\cdot t \cdot \pi (u) \cdot (8\tilde{k})$
is satisfied. Thus by Lemma 4.12 (with
$c\sqrt{t}\geq 32\cdot t \cdot \pi (u) \cdot (8\tilde{k})$
is satisfied. Thus by Lemma 4.12 (with
![]() $k=8\tilde{k}$
) we have
$k=8\tilde{k}$
) we have
![]() $t_{\mathsf{large-cov}}^{(\tilde{k})} \geq t/5 = \Omega (n^2)$
.
$t_{\mathsf{large-cov}}^{(\tilde{k})} \geq t/5 = \Omega (n^2)$
.
5.2. Complete binary tree and two-dimensional torus
In this section, we derive the multiple cover times for the Complete Binary Tree and 2-Dimensional Torus. We treat them together as their proofs have several common elements. Some standard estimates such as return probabilities and other elementary results on trees can be found in Section A.2.
Theorem 5.5.
Let
![]() $G$
be the two-dimensional torus
$G$
be the two-dimensional torus
![]() ${\mathbb{T}}_2$
or the complete binary tree
${\mathbb{T}}_2$
or the complete binary tree
![]() $\mathcal{T}_n$
. Then there exists a constant
$\mathcal{T}_n$
. Then there exists a constant
![]() $c\gt 0$
(independent of
$c\gt 0$
(independent of
![]() $n$
) such that for any
$n$
) such that for any
![]() $1\leq k\leq cn\log n$
,
$1\leq k\leq cn\log n$
,
For worst-case cover time of the binary tree the best previously known bounds differ by multiplicative
![]() $\mathsf{poly}(\!\log n)$
factors [Reference Georgakopoulos, Haslegrave, Sauerwald and Sylvester23]. Using our new
$\mathsf{poly}(\!\log n)$
factors [Reference Georgakopoulos, Haslegrave, Sauerwald and Sylvester23]. Using our new
![]() $\min$
-
$\min$
-
![]() $\max$
and
$\max$
and
![]() $\max$
-
$\max$
-
![]() $\min$
characterisations, and some additional calculations, we can now determine
$\min$
characterisations, and some additional calculations, we can now determine
![]() $t_{\mathsf{cov}}^{(k)}$
up to constants for any
$t_{\mathsf{cov}}^{(k)}$
up to constants for any
![]() $1 \leq k \leq n$
.
$1 \leq k \leq n$
.
Theorem 5.6.
For the complete binary tree
![]() $\mathcal{T}_{n}$
:
$\mathcal{T}_{n}$
:
 $$t_{cov}^{(k)} = \left\{ {\matrix{
{\Theta \left( {{n \over k}{{\log }^2}n} \right)} & {if\,1 \le k \le {{\log }^2}n,} \cr
{\Theta \left( {{n \over {\sqrt k }}\log n} \right){\rm{ }}} & {if\,{{\log }^2}n \le k \le n.{\rm{ }}} \cr
} } \right.$$
$$t_{cov}^{(k)} = \left\{ {\matrix{
{\Theta \left( {{n \over k}{{\log }^2}n} \right)} & {if\,1 \le k \le {{\log }^2}n,} \cr
{\Theta \left( {{n \over {\sqrt k }}\log n} \right){\rm{ }}} & {if\,{{\log }^2}n \le k \le n.{\rm{ }}} \cr
} } \right.$$
The worst-case cover time of the
![]() $2$
d-torus was shown in [Reference Ivaskovic, Kosowski, Pajak, Sauerwald, Vollmer and Vallée31]:
$2$
d-torus was shown in [Reference Ivaskovic, Kosowski, Pajak, Sauerwald, Vollmer and Vallée31]:
Theorem 5.7. ([Reference Ivaskovic, Kosowski, Pajak, Sauerwald, Vollmer and Vallée31]). For the two-dimensional torus
![]() ${\mathbb{T}}_2$
:
${\mathbb{T}}_2$
:
 $$t_{cov}^{(k)} = \left\{ {\matrix{
{\Theta \left( {{n \over k}{{\log }^2}n} \right)} & {if\,1 \le k \le {{\log }^2}n,} \cr
{\Theta \left( {{n \over {\log (k/{{\log }^2}n)}}} \right){\rm{ }}} & {if{{\log }^2}n \le k \le n.} \cr
} } \right.$$
$$t_{cov}^{(k)} = \left\{ {\matrix{
{\Theta \left( {{n \over k}{{\log }^2}n} \right)} & {if\,1 \le k \le {{\log }^2}n,} \cr
{\Theta \left( {{n \over {\log (k/{{\log }^2}n)}}} \right){\rm{ }}} & {if{{\log }^2}n \le k \le n.} \cr
} } \right.$$
Using the tools introduced in Section 4 we can recover the upper bounds in Theorem 5.7 fairly efficiently. However, for the lower bounds in Theorem 5.7 we did not find a way to apply our (or any other) general techniques to give a tight bound easily for all
![]() $k$
. The methods presented in this work give a lower bound tight up to a
$k$
. The methods presented in this work give a lower bound tight up to a
![]() $\log n$
factor however we do not give the details as recovering loose bounds on known quantities is not the goal of this work.
$\log n$
factor however we do not give the details as recovering loose bounds on known quantities is not the goal of this work.
5.2.1. Stationary cover time of the binary tree &
 $2$
d-torus
$2$
d-torus
In this section, we prove Theorem 5.5. The upper bounds are established by applying Lemma 3.5 to both graphs. A matching lower bound is proved by showing that both graphs have a set which is particularly hard to cover.
Proof of Theorem
5.5. For the upper bound, in either graph we have,
![]() $ \sum _{i=0}^t P_{v,v}^i= \mathcal{O}(1+\log t )$
for any
$ \sum _{i=0}^t P_{v,v}^i= \mathcal{O}(1+\log t )$
for any
![]() $v\in V$
and
$v\in V$
and
![]() $t\leq t_{\mathsf{rel}}$
by Lemmas A.4, A.5 and A.2, and that
$t\leq t_{\mathsf{rel}}$
by Lemmas A.4, A.5 and A.2, and that
![]() $t_{\mathsf{mix}} =\mathcal{O}(n )$
for both graphs by [Reference Aldous and Fill2, Eq. 5.59] and [Reference Levin, Peres and Wilmer42, Eq. 5.6]. Thus the upper bound follows directly from Lemma 3.5.
$t_{\mathsf{mix}} =\mathcal{O}(n )$
for both graphs by [Reference Aldous and Fill2, Eq. 5.59] and [Reference Levin, Peres and Wilmer42, Eq. 5.6]. Thus the upper bound follows directly from Lemma 3.5.
We split the lower bound into three cases depending on the value of
![]() $k$
. First, set
$k$
. First, set
and observe that we aim to prove
![]() $t_{\mathsf{cov}}^{(k)}(\pi ) =\Omega (t^*)$
. We now show this in each case.
$t_{\mathsf{cov}}^{(k)}(\pi ) =\Omega (t^*)$
. We now show this in each case.
Case (i) [
![]() $1 \leq k \leq (\!\log n)^{5/3}$
]: First recall the following bound by [Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Theorem 4.8]:
$1 \leq k \leq (\!\log n)^{5/3}$
]: First recall the following bound by [Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Theorem 4.8]:
For both
![]() ${\mathbb{T}}_2$
and
${\mathbb{T}}_2$
and
![]() $\mathcal{T}_n$
we have
$\mathcal{T}_n$
we have
![]() $t_{\mathsf{mix}} =\Theta \! (n )$
,
$t_{\mathsf{mix}} =\Theta \! (n )$
,
![]() $t_{\mathsf{hit}} =\Theta \! (n\log n )$
and
$t_{\mathsf{hit}} =\Theta \! (n\log n )$
and
![]() $t_{\mathsf{cov}} =\Theta \! (n\log ^2 n )$
by [Reference Levin, Peres and Wilmer42, Section 11.3.2] and [Reference Aldous and Fill2, Theorem 6.27], respectively. Recall also that
$t_{\mathsf{cov}} =\Theta \! (n\log ^2 n )$
by [Reference Levin, Peres and Wilmer42, Section 11.3.2] and [Reference Aldous and Fill2, Theorem 6.27], respectively. Recall also that
![]() $t_{\mathsf{cov}}^{(k)}(\pi )\leq \mathcal{O}\!\left (\frac{t_{\mathsf{hit}}\log n}{k}\right ) =\mathcal{O}\!\left (\frac{n\log ^2 n}{k}\right )$
by Theorem 3.2, and so plugging these bounds into (30) gives
$t_{\mathsf{cov}}^{(k)}(\pi )\leq \mathcal{O}\!\left (\frac{t_{\mathsf{hit}}\log n}{k}\right ) =\mathcal{O}\!\left (\frac{n\log ^2 n}{k}\right )$
by Theorem 3.2, and so plugging these bounds into (30) gives
Thus for either graph, if
![]() $1 \leq k \leq (\!\log n)^{5/3}$
, we have
$1 \leq k \leq (\!\log n)^{5/3}$
, we have
 \begin{equation*}t_{\mathsf {cov}}^{(k)}(\pi )\geq t_{\mathsf {cov}}/k -\mathcal {O}\!\left (n\log \log n\right ) - \mathcal {O}\!\left (\frac {n}{\sqrt {k}}\log n\right ) = \Omega \left ( \frac {n\log ^2 n}{k}\right ) = \Omega (t^*).\end{equation*}
\begin{equation*}t_{\mathsf {cov}}^{(k)}(\pi )\geq t_{\mathsf {cov}}/k -\mathcal {O}\!\left (n\log \log n\right ) - \mathcal {O}\!\left (\frac {n}{\sqrt {k}}\log n\right ) = \Omega \left ( \frac {n\log ^2 n}{k}\right ) = \Omega (t^*).\end{equation*}
Case (ii) [
![]() $(\!\log n )^{5/3}\leq k\leq n^{1/2}$
]: Let
$(\!\log n )^{5/3}\leq k\leq n^{1/2}$
]: Let
![]() $t^*$
be as (29) and observe that in this case
$t^*$
be as (29) and observe that in this case
Let
![]() $\widehat{G}\;:\!=\;\widehat{G}(x)$
be the geometric reset graph from Definition 3.7 where
$\widehat{G}\;:\!=\;\widehat{G}(x)$
be the geometric reset graph from Definition 3.7 where
![]() $x=k/(n(\!\log n)^2)$
. We use
$x=k/(n(\!\log n)^2)$
. We use
![]() ${\mathbb{P}}_{u,H}[\!\cdot\! ]$
to denote the law of the (non-lazy) random walk on
${\mathbb{P}}_{u,H}[\!\cdot\! ]$
to denote the law of the (non-lazy) random walk on
![]() $H$
started from
$H$
started from
![]() $u\in V(H)$
. For ease of reading, we prove the next claim on Page 56 after concluding the current proof.
$u\in V(H)$
. For ease of reading, we prove the next claim on Page 56 after concluding the current proof.
Claim 5.8.
Let
![]() $G=\mathcal{T}_n$
or
$G=\mathcal{T}_n$
or
![]() ${\mathbb{T}}_2$
,
${\mathbb{T}}_2$
,
![]() $(\!\log n )^{5/3}\leq k\leq n^{1/2}$
, and
$(\!\log n )^{5/3}\leq k\leq n^{1/2}$
, and
![]() $\widehat{G}\;:\!=\;\widehat{G}(x)$
, where
$\widehat{G}\;:\!=\;\widehat{G}(x)$
, where
![]() $x=\kappa \cdot k/(n(\!\log n)^2)$
for a fixed constant
$x=\kappa \cdot k/(n(\!\log n)^2)$
for a fixed constant
![]() $\kappa \gt 0$
. Then, there exists a subset
$\kappa \gt 0$
. Then, there exists a subset
![]() $S\subseteq V$
such that
$S\subseteq V$
such that
![]() $\log |S| \geq (\!\log n)/100$
and a constant
$\log |S| \geq (\!\log n)/100$
and a constant
![]() $\kappa '\gt 0$
(independent of
$\kappa '\gt 0$
(independent of
![]() $\kappa$
) such that
$\kappa$
) such that
![]() ${\mathbb{E}}_{u,\widehat{G}} \left [\tau _v\right ] \geq \kappa '\cdot n \cdot \log \left (\frac{n\log n}{k}\right )$
for all
${\mathbb{E}}_{u,\widehat{G}} \left [\tau _v\right ] \geq \kappa '\cdot n \cdot \log \left (\frac{n\log n}{k}\right )$
for all
![]() $u,v \in S$
.
$u,v \in S$
.
In light of Claim 5.8 it follows from [Reference Kahn, Kim, Lovász and Vu33, Theorem 1.4] that, for any
![]() $x=\kappa \cdot k/(n(\!\log n)^2)$
,
$x=\kappa \cdot k/(n(\!\log n)^2)$
,
where we note that although [Reference Kahn, Kim, Lovász and Vu33, Theorem 1.4] is stated only for the simple random walk, it holds for all reversible Markov chains, see [Reference Cooper, Kosowski and Yamashita11, Page 4]. Thus, by Lemma 3.11 and (31), there exists some constant
![]() $c\gt 0$
, independent of
$c\gt 0$
, independent of
![]() $\kappa$
, such that for all suitably large
$\kappa$
, such that for all suitably large
![]() $n$
,
$n$
,
We now aim to apply Lemma 3.8 where to begin with we choose the values
![]() $T=cn\log ^2 n$
and
$T=cn\log ^2 n$
and
![]() $C=100$
. Observe that
$C=100$
. Observe that
![]() $T\geq 5Ck$
for large enough
$T\geq 5Ck$
for large enough
![]() $n$
since
$n$
since
![]() $k\leq n^{1/2}$
. Finally, since
$k\leq n^{1/2}$
. Finally, since
![]() $c$
is independent of
$c$
is independent of
![]() $\kappa$
, we can set
$\kappa$
, we can set
![]() $\kappa = 100/c$
such that
$\kappa = 100/c$
such that
![]() $x=\kappa \cdot k/(n(\!\log n)^2)= Ck/T$
. Then, by Lemma 3.8 and (32),
$x=\kappa \cdot k/(n(\!\log n)^2)= Ck/T$
. Then, by Lemma 3.8 and (32),
Case (iii) [
![]() $ n^{1/2}\leq k \leq cn\log n$
]: Let
$ n^{1/2}\leq k \leq cn\log n$
]: Let
![]() $\delta \in (0,1)$
be a small constant to be chosen later, and let
$\delta \in (0,1)$
be a small constant to be chosen later, and let
![]() $c = (\delta/2)^2$
, and
$c = (\delta/2)^2$
, and
![]() $t^*$
be as given by (29). Let
$t^*$
be as given by (29). Let
![]() $u$
be a leaf of the tree
$u$
be a leaf of the tree
![]() $\mathcal{T}_n$
, or any vertex of
$\mathcal{T}_n$
, or any vertex of
![]() ${\mathbb{T}}_2$
, then,
${\mathbb{T}}_2$
, then,
![]() $\sum _{i=0}^{\delta t^*} P_{u,u}^i = \Omega (\!\log\!(\delta t^*) )$
by Lemmas A.4 and A.2, respectively. Then, by an application of Lemma 3.10 (ii) there exists a non-negative constant
$\sum _{i=0}^{\delta t^*} P_{u,u}^i = \Omega (\!\log\!(\delta t^*) )$
by Lemmas A.4 and A.2, respectively. Then, by an application of Lemma 3.10 (ii) there exists a non-negative constant
![]() $C$
, such that
$C$
, such that
 \begin{align} {\mathbb{P}}_{\pi }\!\left [ \tau _u \leq \delta \cdot t^* \right ] &\leq \frac{2\delta \cdot (t^*+1) \cdot \pi (u) }{\sum _{s=0}^{\delta t^*/2} P_{u,u}^s} \notag \\[5pt] &\leq \frac{C\cdot \delta \log n \cdot \log\!( (n/k)\cdot \log n) }{k \cdot \log \left ((\delta/2) \cdot (n/k)\log n \cdot \log \left ((n/k)\cdot \log n\right )\right ) }\nonumber \\[5pt] &= \frac{C\cdot \delta \log n \cdot \log\!( (n/k)\cdot \log n)) }{k \cdot \left (\log\!(\delta/2)+\log\!((n/k)\cdot \log n) + \log\!( \log\!((n/k)\cdot \log n)) \right )}\nonumber \\[5pt] &\leq \frac{2C\delta \log n\cdot \log\!((n/k)\cdot \log n)}{k\cdot \log\!((n/k)\cdot \log n)}\notag \\[5pt] &= \frac{2C\delta \log n}{k}, \end{align}
\begin{align} {\mathbb{P}}_{\pi }\!\left [ \tau _u \leq \delta \cdot t^* \right ] &\leq \frac{2\delta \cdot (t^*+1) \cdot \pi (u) }{\sum _{s=0}^{\delta t^*/2} P_{u,u}^s} \notag \\[5pt] &\leq \frac{C\cdot \delta \log n \cdot \log\!( (n/k)\cdot \log n) }{k \cdot \log \left ((\delta/2) \cdot (n/k)\log n \cdot \log \left ((n/k)\cdot \log n\right )\right ) }\nonumber \\[5pt] &= \frac{C\cdot \delta \log n \cdot \log\!( (n/k)\cdot \log n)) }{k \cdot \left (\log\!(\delta/2)+\log\!((n/k)\cdot \log n) + \log\!( \log\!((n/k)\cdot \log n)) \right )}\nonumber \\[5pt] &\leq \frac{2C\delta \log n\cdot \log\!((n/k)\cdot \log n)}{k\cdot \log\!((n/k)\cdot \log n)}\notag \\[5pt] &= \frac{2C\delta \log n}{k}, \end{align}
where in the last inequality we use that
![]() $k\leq c(n\log n) = (\delta/2)^2 (n\log n)$
, and thus we have that
$k\leq c(n\log n) = (\delta/2)^2 (n\log n)$
, and thus we have that
![]() $\log\!((n/k)\cdot \log n)\geq 2\log\!(\delta/2)$
.
$\log\!((n/k)\cdot \log n)\geq 2\log\!(\delta/2)$
.
We will now apply Lemma 3.9, where for the binary tree
![]() $\mathcal{T}_n$
we choose
$\mathcal{T}_n$
we choose
![]() $S$
as the set of all leaves, and for
$S$
as the set of all leaves, and for
![]() ${\mathbb{T}}_2$
choose
${\mathbb{T}}_2$
choose
![]() $S = V({\mathbb{T}}_2)$
. Thus in either case we have
$S = V({\mathbb{T}}_2)$
. Thus in either case we have
![]() $|S|\min _{v\in S}\pi (v) \geq 1/3$
,
$|S|\min _{v\in S}\pi (v) \geq 1/3$
,
![]() $p\leq \frac{2C\delta \log n}{k}$
by (33) and
$p\leq \frac{2C\delta \log n}{k}$
by (33) and
![]() $2p^2k\lt 1$
since
$2p^2k\lt 1$
since
![]() $k \geq n^{1/2}$
. Thus by Lemma 3.9
$k \geq n^{1/2}$
. Thus by Lemma 3.9
where the last equality follows by taking
![]() $\delta = \frac{1}{12C}$
since
$\delta = \frac{1}{12C}$
since
![]() $k \geq n^{1/2}$
.
$k \geq n^{1/2}$
.
It remains to prove Claim 5.8.
Proof of Claim
5.8. For
![]() $\mathcal{T}_n$
we let
$\mathcal{T}_n$
we let
![]() $S$
be the set of leaves at pairwise distance at least
$S$
be the set of leaves at pairwise distance at least
![]() $(\!\log n)/2$
and in
$(\!\log n)/2$
and in
![]() ${\mathbb{T}}_2$
we take an (almost) evenly spaced sub-lattice where the distance between points next to each other is
${\mathbb{T}}_2$
we take an (almost) evenly spaced sub-lattice where the distance between points next to each other is
![]() $\Theta (n^{1/4})$
. It is easy to see that one can find such an
$\Theta (n^{1/4})$
. It is easy to see that one can find such an
![]() $S$
of polynomial size, in particular we can take
$S$
of polynomial size, in particular we can take
![]() $\log |S|\geq (\!\log n)/100$
.
$\log |S|\geq (\!\log n)/100$
.
We first consider a walk
![]() $\widehat{W}_t$
in
$\widehat{W}_t$
in
![]() $\widehat{G}(x)$
from
$\widehat{G}(x)$
from
![]() $\widehat{\pi }$
(rather than
$\widehat{\pi }$
(rather than
![]() $u$
). Let
$u$
). Let
![]() $N_v(T)$
be the number of visits to
$N_v(T)$
be the number of visits to
![]() $v\in S$
in the interval
$v\in S$
in the interval
![]() $[0,T)$
, where, for some
$[0,T)$
, where, for some
![]() $\delta \gt 0$
,
$\delta \gt 0$
,
Let the random variable
![]() $Y$
be the first time that the walk in
$Y$
be the first time that the walk in
![]() $\widehat{G}(x)$
started from a vertex in
$\widehat{G}(x)$
started from a vertex in
![]() $V(G)$
leaves
$V(G)$
leaves
![]() $V(G)$
to visit
$V(G)$
to visit
![]() $z$
. Observe that
$z$
. Observe that
![]() $Y \sim \operatorname{Geo}(x )$
regardless of the start vertex, and thus
$Y \sim \operatorname{Geo}(x )$
regardless of the start vertex, and thus
![]() ${\mathbb{P}} [Y\geq 1/x] = (1-x)^{1/x} \geq e^{-1}(1-x^2)\geq e^{-2}$
by (1). Conditional on
${\mathbb{P}} [Y\geq 1/x] = (1-x)^{1/x} \geq e^{-1}(1-x^2)\geq e^{-2}$
by (1). Conditional on
![]() $\{Y\geq 1/x\}\cap \{\widehat{W}_0\neq z\}$
the walk has the same law as a walk
$\{Y\geq 1/x\}\cap \{\widehat{W}_0\neq z\}$
the walk has the same law as a walk
![]() $P$
on
$P$
on
![]() $G$
until time
$G$
until time
![]() $1/x$
, as edges not leading to
$1/x$
, as edges not leading to
![]() $z$
all have the same weight in
$z$
all have the same weight in
![]() $\widehat{G}$
. Thus, if
$\widehat{G}$
. Thus, if
![]() $Q$
is the transition matrix of the walk on
$Q$
is the transition matrix of the walk on
![]() $\widehat{G}(x)$
then for any vertex
$\widehat{G}(x)$
then for any vertex
![]() $v\neq z$
, we have
$v\neq z$
, we have
Now, as
![]() $\min (T/2-1, 1/x)=1/x$
, by Lemma 3.10 (ii),
$\min (T/2-1, 1/x)=1/x$
, by Lemma 3.10 (ii),
 \begin{equation*}{\mathbb{E}}_{\widehat {\pi },\widehat {G}} \left [N_v(T) \mid N_v(T)\geq 1\right ] \geq \frac {1}{2}\cdot \sum _{i=0}^{\min (T/2-1, 1/x)} Q_{v,v}^i \geq \frac {e^{-2}}{2}\cdot \sum _{i=0}^{1/x} P_{v,v}^i\geq C\cdot \log\!(1/x), \end{equation*}
\begin{equation*}{\mathbb{E}}_{\widehat {\pi },\widehat {G}} \left [N_v(T) \mid N_v(T)\geq 1\right ] \geq \frac {1}{2}\cdot \sum _{i=0}^{\min (T/2-1, 1/x)} Q_{v,v}^i \geq \frac {e^{-2}}{2}\cdot \sum _{i=0}^{1/x} P_{v,v}^i\geq C\cdot \log\!(1/x), \end{equation*}
for some
![]() $C\gt 0$
fixed by Lemmas A.4 and A.2. Now, for any fixed
$C\gt 0$
fixed by Lemmas A.4 and A.2. Now, for any fixed
![]() $\kappa \gt 0$
, by Lemma 3.10 (ii),
$\kappa \gt 0$
, by Lemma 3.10 (ii),
 \begin{equation*}{\mathbb{P}}_{\widehat {\pi },\widehat {G}}\!\left [N_v(T)\geq 1\right ] = \frac {{\mathbb{E}}_{\widehat {\pi },\widehat {G}} \left [N_v(T)\right ]}{{\mathbb{E}}_{\widehat {\pi },\widehat {G}} \left [N_v(T) \mid N_v(T)\geq 1\right ]} \leq \frac {T/n}{C\cdot \log\!(1/x) } \leq \frac {\delta \log\!\left (\frac {n\log n}{k}\right ) }{C\log\!\left (\frac {n(\!\log n)^2}{\kappa \cdot k}\right )} \leq \frac {\delta }{C},\end{equation*}
\begin{equation*}{\mathbb{P}}_{\widehat {\pi },\widehat {G}}\!\left [N_v(T)\geq 1\right ] = \frac {{\mathbb{E}}_{\widehat {\pi },\widehat {G}} \left [N_v(T)\right ]}{{\mathbb{E}}_{\widehat {\pi },\widehat {G}} \left [N_v(T) \mid N_v(T)\geq 1\right ]} \leq \frac {T/n}{C\cdot \log\!(1/x) } \leq \frac {\delta \log\!\left (\frac {n\log n}{k}\right ) }{C\log\!\left (\frac {n(\!\log n)^2}{\kappa \cdot k}\right )} \leq \frac {\delta }{C},\end{equation*}
since
![]() ${\mathbb{E}}_{\widehat{\pi },\widehat{G}} [N_v(T)]= \widehat{\pi }(v)T\leq T/n$
. Thus, by taking
${\mathbb{E}}_{\widehat{\pi },\widehat{G}} [N_v(T)]= \widehat{\pi }(v)T\leq T/n$
. Thus, by taking
![]() $\delta = C/2\gt 0$
, we have
$\delta = C/2\gt 0$
, we have
Recall
![]() $Y\sim \operatorname{Geo}(x )$
and observe that
$Y\sim \operatorname{Geo}(x )$
and observe that
![]() $1/x\leq n(\!\log n)^{1/3}/\kappa = o(n\sqrt{n})$
since
$1/x\leq n(\!\log n)^{1/3}/\kappa = o(n\sqrt{n})$
since
![]() $k\geq (\!\log n)^{5/3}$
and
$k\geq (\!\log n)^{5/3}$
and
![]() $\kappa \gt 0$
is fixed. Thus
$\kappa \gt 0$
is fixed. Thus
![]() ${\mathbb{P}}_{u,\widehat{G}}[Y\gt n\sqrt{\log n} ] = (1-x)^{n\sqrt{\log n}} = o(1 )$
. Hence, for any
${\mathbb{P}}_{u,\widehat{G}}[Y\gt n\sqrt{\log n} ] = (1-x)^{n\sqrt{\log n}} = o(1 )$
. Hence, for any
![]() $u,v\in S$
,
$u,v\in S$
,
 \begin{align*} {\mathbb{P}}_{u,\widehat{G}}\!\left [ \tau _v \lt Y\right ] &= \sum _{i=0}^{\infty } {\mathbb{P}}_{u,\widehat{G}}\!\left [\tau _v\lt i, Y=i \right ] =o\!\left (1\right ) + \sum _{i=0}^{n\sqrt{\log n }} {\mathbb{P}}_{u,\widehat{G}}\!\left [\tau _v\lt i\mid Y=i \right ]{\mathbb{P}}_{u,\widehat{G}}\!\left [ Y=i \right ]. \end{align*}
\begin{align*} {\mathbb{P}}_{u,\widehat{G}}\!\left [ \tau _v \lt Y\right ] &= \sum _{i=0}^{\infty } {\mathbb{P}}_{u,\widehat{G}}\!\left [\tau _v\lt i, Y=i \right ] =o\!\left (1\right ) + \sum _{i=0}^{n\sqrt{\log n }} {\mathbb{P}}_{u,\widehat{G}}\!\left [\tau _v\lt i\mid Y=i \right ]{\mathbb{P}}_{u,\widehat{G}}\!\left [ Y=i \right ]. \end{align*}
Now, if we condition on the walk in
![]() $\widehat{G}$
not taking an edge to
$\widehat{G}$
not taking an edge to
![]() $z$
up to time
$z$
up to time
![]() $i$
then, since the weights on edges not going to
$i$
then, since the weights on edges not going to
![]() $z$
are all the same, this has the same law as a trajectory in
$z$
are all the same, this has the same law as a trajectory in
![]() $G$
of length
$G$
of length
![]() $i$
. It follows that
$i$
. It follows that
![]() ${\mathbb{P}}_{u,\widehat{G}}[\tau _v\lt i\mid Y=i ] = {\mathbb{P}}_{u,G}[\tau _v\lt i ]$
, and so we have
${\mathbb{P}}_{u,\widehat{G}}[\tau _v\lt i\mid Y=i ] = {\mathbb{P}}_{u,G}[\tau _v\lt i ]$
, and so we have
 \begin{equation} {\mathbb{P}}_{u,\widehat{G}}\!\left [ \tau _v \lt Y\right ] =o\!\left (1\right ) + \sum _{i=0}^{n\sqrt{\log n }} {\mathbb{P}}_{u,G}\!\left [\tau _v\lt i\right ]{\mathbb{P}}_{u,\widehat{G}}\!\left [ Y=i \right ]\leq {\mathbb{P}}_{u,G}\!\left [\tau _v\lt n\sqrt{\log n }\right ]+o\!\left (1\right ) . \end{equation}
\begin{equation} {\mathbb{P}}_{u,\widehat{G}}\!\left [ \tau _v \lt Y\right ] =o\!\left (1\right ) + \sum _{i=0}^{n\sqrt{\log n }} {\mathbb{P}}_{u,G}\!\left [\tau _v\lt i\right ]{\mathbb{P}}_{u,\widehat{G}}\!\left [ Y=i \right ]\leq {\mathbb{P}}_{u,G}\!\left [\tau _v\lt n\sqrt{\log n }\right ]+o\!\left (1\right ) . \end{equation}
For either graph
![]() $G=\mathcal{T}_n,{\mathbb{T}}_2$
we have
$G=\mathcal{T}_n,{\mathbb{T}}_2$
we have
![]() $t_{\mathsf{hit}}(G)=\mathcal{O}(n\log n )$
and
$t_{\mathsf{hit}}(G)=\mathcal{O}(n\log n )$
and
![]() ${\mathbb{E}}_{u,G} [\tau _v]= \Omega(n\log n )$
, where the latter bound is by symmetry as the effective resistance between any two vertices in
${\mathbb{E}}_{u,G} [\tau _v]= \Omega(n\log n )$
, where the latter bound is by symmetry as the effective resistance between any two vertices in
![]() $S$
is
$S$
is
![]() $\Omega (\!\log n )$
. Thus we can apply Lemma A.1 to give
$\Omega (\!\log n )$
. Thus we can apply Lemma A.1 to give
![]() ${\mathbb{P}}_{u,G}[ \tau _v\gt n\sqrt{\log n} ] \gt 1/3$
. Therefore
${\mathbb{P}}_{u,G}[ \tau _v\gt n\sqrt{\log n} ] \gt 1/3$
. Therefore
![]() ${\mathbb{P}}_{u,\widehat{G}}[ \tau _v\gt Y ]\gt 1/3 -o(1 ) \geq 1/4$
by (36). We now extend the distribution
${\mathbb{P}}_{u,\widehat{G}}[ \tau _v\gt Y ]\gt 1/3 -o(1 ) \geq 1/4$
by (36). We now extend the distribution
![]() $\pi$
on
$\pi$
on
![]() $G$
to
$G$
to
![]() $\widehat{G}$
by setting
$\widehat{G}$
by setting
![]() $\pi (z)=0$
, and observe that
$\pi (z)=0$
, and observe that
![]() $\widehat{\pi }(y)\leq \pi (y)$
for all
$\widehat{\pi }(y)\leq \pi (y)$
for all
![]() $y\neq z$
. A walk on
$y\neq z$
. A walk on
![]() $\widehat{G}$
at
$\widehat{G}$
at
![]() $z$
moves to a vertex of
$z$
moves to a vertex of
![]() $ V(\widehat{G})$
distributed according to
$ V(\widehat{G})$
distributed according to
![]() $\pi$
in the next step, thus
$\pi$
in the next step, thus
For any
![]() $i\geq 0$
,
$i\geq 0$
,
![]() ${\mathbb{E}}_{u,\widehat{G}} [ \tau _v \, |\, \tau _v\gt Y, Y=i] = i+2 +{\mathbb{E}}_{\pi,\widehat{G}} [ \tau _v]\geq {\mathbb{E}}_{\widehat{\pi },\widehat{G}} [ \tau _v]/3$
. To see the first equality note that at time
${\mathbb{E}}_{u,\widehat{G}} [ \tau _v \, |\, \tau _v\gt Y, Y=i] = i+2 +{\mathbb{E}}_{\pi,\widehat{G}} [ \tau _v]\geq {\mathbb{E}}_{\widehat{\pi },\widehat{G}} [ \tau _v]/3$
. To see the first equality note that at time
![]() $i$
the walk has not yet hit
$i$
the walk has not yet hit
![]() $v$
and takes a step to
$v$
and takes a step to
![]() $z$
, thus two steps later the walk is at a vertex sampled from
$z$
, thus two steps later the walk is at a vertex sampled from
![]() $\pi$
. Hence, when
$\pi$
. Hence, when
![]() $n$
is large, for any
$n$
is large, for any
![]() $u,v\in S$
by (35)
$u,v\in S$
by (35)
The claim follows from (34) since
![]() $\delta =C/2\gt 0$
and
$\delta =C/2\gt 0$
and
![]() $C\gt 0$
is fixed and independent of
$C\gt 0$
is fixed and independent of
![]() $\kappa$
.
$\kappa$
.
5.2.2. Worst-case binary tree
The following result, needed for Theorem 5.6, gives a bound on the partial mixing time.
Lemma 5.9.
For the complete binary tree
![]() $\mathcal{T}_n$
and any
$\mathcal{T}_n$
and any
![]() $1 \leq \tilde{k} \leq k/100$
,
$1 \leq \tilde{k} \leq k/100$
,
 \begin{equation*}t_{\mathsf {mix}}^{(\tilde {k},k)} =\mathcal {O}\!\left (\frac {\tilde {k}}{k} \cdot n + \log n\right ).\end{equation*}
\begin{equation*}t_{\mathsf {mix}}^{(\tilde {k},k)} =\mathcal {O}\!\left (\frac {\tilde {k}}{k} \cdot n + \log n\right ).\end{equation*}
Proof. Let
![]() $r$
be the root and
$r$
be the root and
![]() $s_r(t)$
be the separation distance from
$s_r(t)$
be the separation distance from
![]() $r$
. We begin with two claims, which will be verified once we finish the current proof.
$r$
. We begin with two claims, which will be verified once we finish the current proof.
Claim 5.10.
There exists some
![]() $C\lt \infty$
such that
$C\lt \infty$
such that
![]() $s_r(t)\leq n^{-10}$
for any
$s_r(t)\leq n^{-10}$
for any
![]() $t\geq t_0=C\log n$
.
$t\geq t_0=C\log n$
.
Claim 5.11.
For any
![]() $u\in V$
,
$u\in V$
,
![]() $\frac{50k\log n}{n} \leq \tilde{k}\leq \frac{k}{100}$
and
$\frac{50k\log n}{n} \leq \tilde{k}\leq \frac{k}{100}$
and
![]() $t_1=\frac{50\tilde{k} n}{k}$
we have
$t_1=\frac{50\tilde{k} n}{k}$
we have
![]() ${\mathbb{P}}_{u}[\tau _r \leq t_1 ] \geq 2\tilde k/k$
.
${\mathbb{P}}_{u}[\tau _r \leq t_1 ] \geq 2\tilde k/k$
.
From these two claims, we conclude that, for any pair of vertices
![]() $v,u$
, and
$v,u$
, and
![]() $\frac{50k\log n}{n} \leq \tilde{k}\leq \frac{k}{100}$
,
$\frac{50k\log n}{n} \leq \tilde{k}\leq \frac{k}{100}$
,
 \begin{align*} P_{u,v}^{t_1+t_0} &\geq \sum _{s=0}^{t_1} {\mathbb{P}}_{u}\!\left [\tau _r =s\right ]{\mathbb{P}}_{r}\!\left [X_{t_1+t_0-s}=v\right ] \geq \sum _{s=0}^{t_1} {\mathbb{P}}_{v}\!\left [\tau _r =s\right ] \pi (v)(1-n^{-10}) \nonumber \geq \frac{2\tilde k}{k}\cdot \frac{\pi (v)}{2} = \frac{\tilde k}{k}\pi (v), \end{align*}
\begin{align*} P_{u,v}^{t_1+t_0} &\geq \sum _{s=0}^{t_1} {\mathbb{P}}_{u}\!\left [\tau _r =s\right ]{\mathbb{P}}_{r}\!\left [X_{t_1+t_0-s}=v\right ] \geq \sum _{s=0}^{t_1} {\mathbb{P}}_{v}\!\left [\tau _r =s\right ] \pi (v)(1-n^{-10}) \nonumber \geq \frac{2\tilde k}{k}\cdot \frac{\pi (v)}{2} = \frac{\tilde k}{k}\pi (v), \end{align*}
thus for
![]() $\tilde{k}$
as above the result follows from definition (15) of
$\tilde{k}$
as above the result follows from definition (15) of
![]() $t_{\mathsf{mix}}(\tilde{k},k)$
. For
$t_{\mathsf{mix}}(\tilde{k},k)$
. For
![]() $\tilde{k}\leq \frac{50k\log n}{n}$
the result follows since
$\tilde{k}\leq \frac{50k\log n}{n}$
the result follows since
![]() $t_{\mathsf{mix}}(\tilde{k},k)$
is increasing in
$t_{\mathsf{mix}}(\tilde{k},k)$
is increasing in
![]() $\tilde{k}$
.
$\tilde{k}$
.
Proof of Claim
5.10. Let
![]() $Y_t$
be the distance from
$Y_t$
be the distance from
![]() $X_t$
to the root
$X_t$
to the root
![]() $r$
, where
$r$
, where
![]() $X_t$
is a lazy random walk starting from
$X_t$
is a lazy random walk starting from
![]() $r$
. Then
$r$
. Then
![]() $Y_t$
is a biased random walk (towards root (left) w.p.
$Y_t$
is a biased random walk (towards root (left) w.p.
![]() $1/6$
, towards leaves (right) w.p.
$1/6$
, towards leaves (right) w.p.
![]() $2/6$
and stay put w.p.
$2/6$
and stay put w.p.
![]() $1/2$
) on the path
$1/2$
) on the path
![]() $0,\ldots, h-1$
with reflecting barriers, and
$0,\ldots, h-1$
with reflecting barriers, and
![]() $Y_0 = 0$
. Consider
$Y_0 = 0$
. Consider
![]() $Y'_{\!\!t}$
to be an independent random walk with the same transition matrix as
$Y'_{\!\!t}$
to be an independent random walk with the same transition matrix as
![]() $Y_t$
but starting from distribution
$Y_t$
but starting from distribution
![]() $\mu$
that denotes the stationary distribution of the biased walk on the path. To couple the walks we assume that
$\mu$
that denotes the stationary distribution of the biased walk on the path. To couple the walks we assume that
![]() $Y'$
starts at a vertex
$Y'$
starts at a vertex
![]() $i\gt 0$
(or else it has already met
$i\gt 0$
(or else it has already met
![]() $Y$
), then both walks move independently unless
$Y$
), then both walks move independently unless
![]() $Y'$
is next to
$Y'$
is next to
![]() $Y$
(thus to the right of it). In this case we sample
$Y$
(thus to the right of it). In this case we sample
![]() $Y'$
first then if
$Y'$
first then if
![]() $Y'$
moves left then
$Y'$
moves left then
![]() $Y$
stays put (and they meet) otherwise,
$Y$
stays put (and they meet) otherwise,
![]() $Y$
moves either left, right or stays with probabilities
$Y$
moves either left, right or stays with probabilities
![]() $1/5$
,
$1/5$
,
![]() $2/5$
and
$2/5$
and
![]() $2/5$
, respectively.
$2/5$
, respectively.
Now, notice that
![]() $Y$
and
$Y$
and
![]() $Y'$
must have met by the time that
$Y'$
must have met by the time that
![]() $Y$
reaches
$Y$
reaches
![]() $h-1$
. We can upper bound
$h-1$
. We can upper bound
![]() ${\mathbb{P}} [Y_t\leq h-1]$
by
${\mathbb{P}} [Y_t\leq h-1]$
by
![]() ${\mathbb{P}} [\!\sum _{i=1}^t Z_i\leq h-1]$
, where
${\mathbb{P}} [\!\sum _{i=1}^t Z_i\leq h-1]$
, where
![]() $Z_i$
are i.i.d. random variable that take value
$Z_i$
are i.i.d. random variable that take value
![]() $1$
w.p
$1$
w.p
![]() $2/6$
, value
$2/6$
, value
![]() $-1$
w.p
$-1$
w.p
![]() $1/6$
, and value
$1/6$
, and value
![]() $0$
w.p
$0$
w.p
![]() $1/2$
. Since
$1/2$
. Since
![]() $h = \log _2 n$
and by choosing
$h = \log _2 n$
and by choosing
![]() $t_0 = C\log _2n$
with
$t_0 = C\log _2n$
with
![]() $C$
large enough, by a simple application of Chernoff’s bound, we have that
$C$
large enough, by a simple application of Chernoff’s bound, we have that
![]() ${\mathbb{P}} [\sum _{i=1}^t Z_i\leq h-1] \leq n^{-12}$
. We conclude that the probability that
${\mathbb{P}} [\sum _{i=1}^t Z_i\leq h-1] \leq n^{-12}$
. We conclude that the probability that
![]() $Y_t$
and
$Y_t$
and
![]() $Y'_{\!\!t}$
do not meet in
$Y'_{\!\!t}$
do not meet in
![]() $\mathcal{O}(\!\log n )$
steps is
$\mathcal{O}(\!\log n )$
steps is
![]() $n^{-12}$
. By the standard coupling characterisation of the total variation distance ([Reference Levin, Peres and Wilmer42, Proposition 4.7]), we have
$n^{-12}$
. By the standard coupling characterisation of the total variation distance ([Reference Levin, Peres and Wilmer42, Proposition 4.7]), we have
![]() $||{\mathbb{P}}_{0}[Y_t=\cdot ]-\!\mu (\cdot )||_{\textrm{TV}}\leq n^{-12}$
, and thus for all
$||{\mathbb{P}}_{0}[Y_t=\cdot ]-\!\mu (\cdot )||_{\textrm{TV}}\leq n^{-12}$
, and thus for all
![]() $i$
,
$i$
,
![]() ${\mathbb{P}}_{0}[Y_t=i ]-\mu (i) \geq -n^{-12}$
. By symmetry, for any vertex at height
${\mathbb{P}}_{0}[Y_t=i ]-\mu (i) \geq -n^{-12}$
. By symmetry, for any vertex at height
![]() $i$
in the binary tree we have
$i$
in the binary tree we have
![]() ${\mathbb{P}}_{r}[X_t = v ] -\mu (i)/ 2^i \geq - n^{-12}$
, since
${\mathbb{P}}_{r}[X_t = v ] -\mu (i)/ 2^i \geq - n^{-12}$
, since
![]() $\mu (i)/2^i = \pi (v)$
. We conclude that
$\mu (i)/2^i = \pi (v)$
. We conclude that
![]() ${\mathbb{P}}_{r}[X_t=v ]\geq \pi (v)\cdot (1-{n^{-10}} )$
for any
${\mathbb{P}}_{r}[X_t=v ]\geq \pi (v)\cdot (1-{n^{-10}} )$
for any
![]() $v\in V(\mathcal{T}_n)$
as claimed.
$v\in V(\mathcal{T}_n)$
as claimed.
Proof of Claim
5.11. We first bound the probability started from
![]() $\pi$
. By Lemma A.3 we have
$\pi$
. By Lemma A.3 we have
![]() $\sum _{s=0}^{t_1} P_{r,r}^s \leq 2+8t_1/n$
, where
$\sum _{s=0}^{t_1} P_{r,r}^s \leq 2+8t_1/n$
, where
![]() $r$
is the root. Therefore, by Lemma 3.10 (ii), we have
$r$
is the root. Therefore, by Lemma 3.10 (ii), we have
Note that the worst-case for our claim is when
![]() $v\in \mathcal{L}$
is a leaf, so we assume this. Denote by
$v\in \mathcal{L}$
is a leaf, so we assume this. Denote by
![]() $\tau _{\mathcal{L}}$
the first time the random walk hits a leaf, then
$\tau _{\mathcal{L}}$
the first time the random walk hits a leaf, then
![]() ${\mathbb{P}}_{\pi }\!\left [\tau _r\lt \tau _{\mathcal{L}}\right ] \leq \frac{8\log n}{n}$
by Lemma A.3, thus
${\mathbb{P}}_{\pi }\!\left [\tau _r\lt \tau _{\mathcal{L}}\right ] \leq \frac{8\log n}{n}$
by Lemma A.3, thus
 \begin{align} {\mathbb{P}}_{\pi }\!\left [\tau _r\leq t_1\right ] &\leq {\mathbb{P}}_{\pi }\!\left [\tau _r\leq t_1, \tau _r\gt \tau _{\mathcal{L}}\right ]+ {\mathbb{P}}_{\pi }\!\left [\tau _r\lt \tau _{\mathcal{L}}\right ]\nonumber \\[5pt] &\leq {\mathbb{P}}_{\pi }\!\left [\tau _r\leq t_1, \tau _r\gt \tau _{\mathcal{L}}, \tau _{\mathcal{L}}\leq c\log n\right ]+{\mathbb{P}}_{\pi }\!\left [\tau _{\mathcal{L}}\gt c\log n\right ]+ \frac{8\log n}{n} \nonumber \\[5pt] &\leq \sum _{s=0}^{\lfloor c\log n \rfloor } {\mathbb{P}}_{v}\!\left [\tau _r\leq t_1-s\right ]{\mathbb{P}}_{\pi }\!\left [\tau _{\mathcal{L}} =s\right ]+\frac{9\log n}{n} \end{align}
\begin{align} {\mathbb{P}}_{\pi }\!\left [\tau _r\leq t_1\right ] &\leq {\mathbb{P}}_{\pi }\!\left [\tau _r\leq t_1, \tau _r\gt \tau _{\mathcal{L}}\right ]+ {\mathbb{P}}_{\pi }\!\left [\tau _r\lt \tau _{\mathcal{L}}\right ]\nonumber \\[5pt] &\leq {\mathbb{P}}_{\pi }\!\left [\tau _r\leq t_1, \tau _r\gt \tau _{\mathcal{L}}, \tau _{\mathcal{L}}\leq c\log n\right ]+{\mathbb{P}}_{\pi }\!\left [\tau _{\mathcal{L}}\gt c\log n\right ]+ \frac{8\log n}{n} \nonumber \\[5pt] &\leq \sum _{s=0}^{\lfloor c\log n \rfloor } {\mathbb{P}}_{v}\!\left [\tau _r\leq t_1-s\right ]{\mathbb{P}}_{\pi }\!\left [\tau _{\mathcal{L}} =s\right ]+\frac{9\log n}{n} \end{align}
the last inequality holds as
![]() ${\mathbb{P}}_{\pi }[\tau _{\mathcal{L}}\gt c\log n ]\leq (\!\log n )/n$
, for
${\mathbb{P}}_{\pi }[\tau _{\mathcal{L}}\gt c\log n ]\leq (\!\log n )/n$
, for
![]() $c$
large by using the Chernoff’s bound and the fact the height of a walk on the tree is a biased walk on a path with reflective barriers (as was used in the proof of Claim 5.10). Thus, by (37) we have
$c$
large by using the Chernoff’s bound and the fact the height of a walk on the tree is a biased walk on a path with reflective barriers (as was used in the proof of Claim 5.10). Thus, by (37) we have
Since
![]() $(50\log n)/n\leq \tilde{k}/k\leq 1/100$
we conclude that
$(50\log n)/n\leq \tilde{k}/k\leq 1/100$
we conclude that
 \begin{equation*}{\mathbb{P}}_{u}\!\left [\tau _r\leq t_1\right ] \geq \frac {t_1}{2n + 8t_1} - \frac {9\log n}{n} \geq \frac {1}{3}\cdot \frac {t_1}{2n + 8t_1} = \frac {50\tilde {k}/k}{6\left (1 + 4\cdot 50\tilde {k}/k \right ) }\geq \frac {2\tilde {k}}{k},\end{equation*}
\begin{equation*}{\mathbb{P}}_{u}\!\left [\tau _r\leq t_1\right ] \geq \frac {t_1}{2n + 8t_1} - \frac {9\log n}{n} \geq \frac {1}{3}\cdot \frac {t_1}{2n + 8t_1} = \frac {50\tilde {k}/k}{6\left (1 + 4\cdot 50\tilde {k}/k \right ) }\geq \frac {2\tilde {k}}{k},\end{equation*}
as desired.
We now prove a lemma which may be regarded as a large-hitting time – since the random walk starts at a leaf in the left-subtree, and the goal is to hit any vertex in the right-subtree.
Lemma 5.12.
Let
![]() $\mathcal{T}_{n}$
be a complete binary tree rooted at
$\mathcal{T}_{n}$
be a complete binary tree rooted at
![]() $r$
, then for any leaf
$r$
, then for any leaf
![]() $\ell$
and any
$\ell$
and any
![]() $t \geq 1$
$t \geq 1$
Proof. We first would like to prove that
![]() $P_{\ell,r}^t \leq 6/n$
for any
$P_{\ell,r}^t \leq 6/n$
for any
![]() $t \geq 1$
. However, this follows immediately by reversibility since
$t \geq 1$
. However, this follows immediately by reversibility since
![]() $P_{r,\ell }^t \leq 3/n$
, as a random walk from
$P_{r,\ell }^t \leq 3/n$
, as a random walk from
![]() $r$
will have a uniform probability over all
$r$
will have a uniform probability over all
![]() $2^{h}\geq n/3$
leaves by symmetry. Hence, for any
$2^{h}\geq n/3$
leaves by symmetry. Hence, for any
![]() $t\leq n$
, we have
$t\leq n$
, we have
![]() $ {\mathbb{P}}_{\ell }[ \tau _{r} \leq t ] \leq \sum _{s=0}^t P_{\ell,r}^s \leq 6t/n$
by Markov’s inequality.
$ {\mathbb{P}}_{\ell }[ \tau _{r} \leq t ] \leq \sum _{s=0}^t P_{\ell,r}^s \leq 6t/n$
by Markov’s inequality.
Finally we are ready to prove the worst-case cover time for the binary tree.
Proof of Theorem
5.6. The results holds immediately for
![]() $k=1$
by known results of cover times of binary trees. We proceed by a case analysis.
$k=1$
by known results of cover times of binary trees. We proceed by a case analysis.
Case (i) [
![]() $2 \leq k \leq (\!\log n)^2$
]: Choose
$2 \leq k \leq (\!\log n)^2$
]: Choose
![]() $\tilde k = \lfloor k/2 \rfloor$
, then by Lemma 4.3 the time for
$\tilde k = \lfloor k/2 \rfloor$
, then by Lemma 4.3 the time for
![]() $\tilde k$
walks to mix is bounded by a constant times the single walk mixing time, which is
$\tilde k$
walks to mix is bounded by a constant times the single walk mixing time, which is
![]() $\Theta (n)$
for the case of the binary tree. Also, we have
$\Theta (n)$
for the case of the binary tree. Also, we have
![]() $t_{\mathsf{cov}}^{(k)}= \mathcal{O}( t_{\mathsf{cov}}^{(\tilde k)}(\pi ) )= \mathcal{O}( (n/\tilde k) (\!\log n)^2 )$
by Theorem 5.5. Therefore, by Theorem 4.7 the upper bound follows. For the lower bound we have
$t_{\mathsf{cov}}^{(k)}= \mathcal{O}( t_{\mathsf{cov}}^{(\tilde k)}(\pi ) )= \mathcal{O}( (n/\tilde k) (\!\log n)^2 )$
by Theorem 5.5. Therefore, by Theorem 4.7 the upper bound follows. For the lower bound we have
![]() $t_{\mathsf{cov}}^{(k)}\geq t_{\mathsf{cov}}^{(k)}(\pi )$
, thus the first part of the formula has been shown.
$t_{\mathsf{cov}}^{(k)}\geq t_{\mathsf{cov}}^{(k)}(\pi )$
, thus the first part of the formula has been shown.
Case (ii) [
![]() $(\!\log n)^2\leq k \leq n$
]: Again, as shown in Theorem 5.5, for any
$(\!\log n)^2\leq k \leq n$
]: Again, as shown in Theorem 5.5, for any
![]() $1 \leq \tilde{k} \leq k$
$1 \leq \tilde{k} \leq k$
Also by Lemma 5.9, for any
![]() $1\leq \tilde{k}\leq k/100$
, we have
$1\leq \tilde{k}\leq k/100$
, we have
 \begin{equation*} t_{\mathsf {mix}}^{(\tilde {k},k)} = \mathcal {O}\!\left ( \frac {\tilde {k}}{k} \cdot n + \log n \right ). \end{equation*}
\begin{equation*} t_{\mathsf {mix}}^{(\tilde {k},k)} = \mathcal {O}\!\left ( \frac {\tilde {k}}{k} \cdot n + \log n \right ). \end{equation*}
To balance the last two upper bounds, we choose
![]() $\tilde{k} = \lfloor (\sqrt{k} \cdot \log n)/100\rfloor$
so that
$\tilde{k} = \lfloor (\sqrt{k} \cdot \log n)/100\rfloor$
so that
and the upper bound follows from Theorem 4.7.
To prove a matching lower bound, let
![]() $\tilde{k}=\lfloor \sqrt{k} \cdot \log n \rfloor$
. Assume that all
$\tilde{k}=\lfloor \sqrt{k} \cdot \log n \rfloor$
. Assume that all
![]() $k$
random walks start from an arbitrary but fixed leaf from the left subtree of
$k$
random walks start from an arbitrary but fixed leaf from the left subtree of
![]() $r$
. Let
$r$
. Let
![]() $t = (n/6) \cdot \tilde{k}/k$
. The number of walks that reach the root by time
$t = (n/6) \cdot \tilde{k}/k$
. The number of walks that reach the root by time
![]() $t$
has binomial distribution
$t$
has binomial distribution
![]() $\operatorname{Bin}\!( k,p )$
with parameters
$\operatorname{Bin}\!( k,p )$
with parameters
![]() $k$
and
$k$
and
![]() $p$
where
$p$
where
![]() $p= {\mathbb{P}}_{l}[ \tau _{r} \leq t ] \leq 6t/n = \tilde{k}/k$
by Lemma 5.12. Thus the expected number of walks to reach to root within
$p= {\mathbb{P}}_{l}[ \tau _{r} \leq t ] \leq 6t/n = \tilde{k}/k$
by Lemma 5.12. Thus the expected number of walks to reach to root within
![]() $t$
steps is upper bounded by the integer
$t$
steps is upper bounded by the integer
![]() $\tilde k$
and so is the median. Therefore with probability at least
$\tilde k$
and so is the median. Therefore with probability at least
![]() $1/2$
, at most
$1/2$
, at most
![]() $\tilde{k}$
out of the
$\tilde{k}$
out of the
![]() $k$
walks reach the root vertex
$k$
walks reach the root vertex
![]() $r$
by time
$r$
by time
![]() $t$
. Once we have
$t$
. Once we have
![]() $\tilde{k}$
walks at the root
$\tilde{k}$
walks at the root
![]() $r$
, we consider the problem of covering the right sub-tree of
$r$
, we consider the problem of covering the right sub-tree of
![]() $r$
with root
$r$
with root
![]() $r_1$
(which has
$r_1$
(which has
![]() $2^{d-1}-1 = \Theta (n)$
vertices), assuming that
$2^{d-1}-1 = \Theta (n)$
vertices), assuming that
![]() $\tilde{k}$
walks start at the root
$\tilde{k}$
walks start at the root
![]() $r_1$
(at step
$r_1$
(at step
![]() $0$
). Since we are looking for a lower bound we can assume that no walks leave the sub-tree and so the problem reduces to compute a lower bound of the cover time of a binary tree with
$0$
). Since we are looking for a lower bound we can assume that no walks leave the sub-tree and so the problem reduces to compute a lower bound of the cover time of a binary tree with
![]() $\tilde k$
walks from the root of the tree.
$\tilde k$
walks from the root of the tree.
Since the
![]() $\tilde k$
walks start from the root, the time it takes to cover the whole set of vertices of the binary tree is lower-bounded by the time it takes to cover the set of leaves (starting from the root). We claim that the previous quantity is, again, lower-bounded by starting the walks from the stationary distribution. To see this, for each walk, independently sample a height
$\tilde k$
walks start from the root, the time it takes to cover the whole set of vertices of the binary tree is lower-bounded by the time it takes to cover the set of leaves (starting from the root). We claim that the previous quantity is, again, lower-bounded by starting the walks from the stationary distribution. To see this, for each walk, independently sample a height
![]() $H$
with probability proportional to the sum of the degrees in such a height, then stop the walk when it reaches height
$H$
with probability proportional to the sum of the degrees in such a height, then stop the walk when it reaches height
![]() $H$
for first time. A simple analysis shows that the distribution of the vertex where the walk stops is the stationary distribution. Note that before stopping the walk cannot have reached a leaf. Hence, we can ignore the time it takes to stop the walks, start all the random walks from the stationary distribution, and, for a lower bound, only consider the expected time to cover the leaves. We can apply the same argument as in the proof of Theorem 5.5 (an application of Lemma 3.9 with
$H$
for first time. A simple analysis shows that the distribution of the vertex where the walk stops is the stationary distribution. Note that before stopping the walk cannot have reached a leaf. Hence, we can ignore the time it takes to stop the walks, start all the random walks from the stationary distribution, and, for a lower bound, only consider the expected time to cover the leaves. We can apply the same argument as in the proof of Theorem 5.5 (an application of Lemma 3.9 with
![]() $S$
taken to be a well spaced subset of the leaves) to lower bound the time taken to cover the leaves. Therefore, we conclude that there exists a constant
$S$
taken to be a well spaced subset of the leaves) to lower bound the time taken to cover the leaves. Therefore, we conclude that there exists a constant
![]() $c\gt 0$
such that the expected time it takes to cover the leaves with
$c\gt 0$
such that the expected time it takes to cover the leaves with
![]() $\tilde k$
walks starting from
$\tilde k$
walks starting from
![]() $\pi$
is bounded from below by
$\pi$
is bounded from below by
Recall that with probability at least
![]() $1/2$
, at most
$1/2$
, at most
![]() $\tilde{k}$
walks reach the root by time
$\tilde{k}$
walks reach the root by time
![]() $(n/6)\cdot \tilde{k}/k$
, thus,
$(n/6)\cdot \tilde{k}/k$
, thus,
 \begin{equation*} t_{\mathsf {cov}}^{(k)} \geq \frac {1}{2}\cdot \min \left ( \frac {n}{6} \cdot \frac {\tilde {k}}{k},\; c\cdot \frac {n\log n }{\tilde {k}}\log \left ( \frac {n\log n }{\tilde {k}}\right ) \right ). \end{equation*}
\begin{equation*} t_{\mathsf {cov}}^{(k)} \geq \frac {1}{2}\cdot \min \left ( \frac {n}{6} \cdot \frac {\tilde {k}}{k},\; c\cdot \frac {n\log n }{\tilde {k}}\log \left ( \frac {n\log n }{\tilde {k}}\right ) \right ). \end{equation*}
Since we set
![]() $\tilde{k} = \lfloor \sqrt{k} \cdot \log n \rfloor$
earlier, we obtain
$\tilde{k} = \lfloor \sqrt{k} \cdot \log n \rfloor$
earlier, we obtain
![]() $t_{\mathsf{cov}}^{(k)} = \Omega \left (\frac{n \log n }{\sqrt{k}}\right )$
.
$t_{\mathsf{cov}}^{(k)} = \Omega \left (\frac{n \log n }{\sqrt{k}}\right )$
.
5.2.3. Worst-case
 $2$
d-torus
$2$
d-torus
Recall that Lemma 5.4 in Section 5.1 bounds the partial mixing time of the
![]() $d$
-dim torus. We now use this and our stationary cover time bounds to prove the upper bound in Theorem 5.7.
$d$
-dim torus. We now use this and our stationary cover time bounds to prove the upper bound in Theorem 5.7.
Proof of the Upper Bound in Theorem
5.7. Observe that the case
![]() $k=1$
is immediate by known results on the cover time of the torus. Now, by Lemma 5.4, for any
$k=1$
is immediate by known results on the cover time of the torus. Now, by Lemma 5.4, for any
![]() $1\leq \tilde{k}\leq k/2$
we have
$1\leq \tilde{k}\leq k/2$
we have
 \begin{equation} t_{\mathsf{mix}}^{(\tilde{k},k)} = \mathcal{O}\!\left ( \frac{n}{ \log\!( k/ \tilde{k} )} \right ). \end{equation}
\begin{equation} t_{\mathsf{mix}}^{(\tilde{k},k)} = \mathcal{O}\!\left ( \frac{n}{ \log\!( k/ \tilde{k} )} \right ). \end{equation}
Further, by Theorem 5.5, we have
Case (i) [
![]() $2 \leq k \leq 2(\!\log n)^2$
]: Choose
$2 \leq k \leq 2(\!\log n)^2$
]: Choose
![]() $\tilde{k}= \lfloor k/2 \rfloor$
, and the bound on
$\tilde{k}= \lfloor k/2 \rfloor$
, and the bound on
![]() $t_{\mathsf{cov}}^{(k)}(\pi )$
dominates, and we obtain
$t_{\mathsf{cov}}^{(k)}(\pi )$
dominates, and we obtain
![]() $t_{\mathsf{cov}}^{(k)}= \mathcal{O}( (n/k) \log ^2 n )$
, by Theorem 4.7. The lower bound follows by
$t_{\mathsf{cov}}^{(k)}= \mathcal{O}( (n/k) \log ^2 n )$
, by Theorem 4.7. The lower bound follows by
![]() $t_{\mathsf{cov}}^{(k)}\geq t_{\mathsf{cov}}^{(k)}(\pi )$
.
$t_{\mathsf{cov}}^{(k)}\geq t_{\mathsf{cov}}^{(k)}(\pi )$
.
Case (ii) [
![]() $ 2(\!\log n)^2\leq n$
, upper bound only]: We now prove (only) the upper bound in the remaining case
$ 2(\!\log n)^2\leq n$
, upper bound only]: We now prove (only) the upper bound in the remaining case
![]() $2(\!\log n)^2 \leq k \leq n$
. We choose
$2(\!\log n)^2 \leq k \leq n$
. We choose
![]() $ \tilde{k} = \lfloor (\!\log n)^2 \cdot \log\!(\!\log k/(\!\log n)^2)\rfloor$
and obtain
$ \tilde{k} = \lfloor (\!\log n)^2 \cdot \log\!(\!\log k/(\!\log n)^2)\rfloor$
and obtain
which is of the same order as the upper bound of
![]() $t_{\mathsf{mix}}^{(\tilde{k},k)}$
in (38), since
$t_{\mathsf{mix}}^{(\tilde{k},k)}$
in (38), since
![]() $\log\!( (a/b) \log\!(a/b) )= \Theta ( \log\!(a/b))$
, thus the result follows from Theorem 4.7.
$\log\!( (a/b) \log\!(a/b) )= \Theta ( \log\!(a/b))$
, thus the result follows from Theorem 4.7.
5.3. Expanders and preferential attachment
Formally, an expander is a (sequence of) graphs
![]() $(G_n)_{n \geq 1}$
such that for all
$(G_n)_{n \geq 1}$
such that for all
![]() $n \geq 1$
:
$n \geq 1$
:
![]() $(i)$
$(i)$
![]() $G_n$
is connected,
$G_n$
is connected,
![]() $(ii)$
$(ii)$
![]() $G_n$
has
$G_n$
has
![]() $n$
vertices, and
$n$
vertices, and
![]() $(iii)$
$(iii)$
![]() $t_{\mathsf{rel}}(G_n) = 1/(1-\lambda _2)\leq C$
for some constant
$t_{\mathsf{rel}}(G_n) = 1/(1-\lambda _2)\leq C$
for some constant
![]() $C\gt 0$
independent of
$C\gt 0$
independent of
![]() $n$
, where
$n$
, where
![]() $\lambda _2$
is the second largest eigenvalue of the transition matrix. Equivalently, due to Cheeger’s inequality, a graph is an expander if
$\lambda _2$
is the second largest eigenvalue of the transition matrix. Equivalently, due to Cheeger’s inequality, a graph is an expander if
![]() $\inf _n \Phi (G_n) \gt 0$
.
$\inf _n \Phi (G_n) \gt 0$
.
All previous works [Reference Alon, Avin, Koucký, Kozma, Lotker and Tuttle5, Reference Efremenko, Reingold, Dinur, Jansen, Naor and Rolim19, Reference Elsässer and Sauerwald20] on multiple random walks required expanders to be regular (or regular up to constants). Here, we allow a broader class of expanders — our methods can treat any graph with bounded relaxation time provided it satisfies
![]() $\pi _{\min }=\Omega (1/n)$
. This class includes some graphs with heavy-tailed degree distributions as long as they have a constant average degree. Such non-regular expanders are quite common, as they include graph models for the internet such as preferential attachment graphs [Reference Mihail, Papadimitriou and Saberi48].
$\pi _{\min }=\Omega (1/n)$
. This class includes some graphs with heavy-tailed degree distributions as long as they have a constant average degree. Such non-regular expanders are quite common, as they include graph models for the internet such as preferential attachment graphs [Reference Mihail, Papadimitriou and Saberi48].
Theorem 5.13.
For any expander with
![]() $\pi _{\min }=\Omega (1/n)$
, for any
$\pi _{\min }=\Omega (1/n)$
, for any
![]() $1 \leq k \leq n$
,
$1 \leq k \leq n$
,
Proof. Note that the case
![]() $k = 1$
follows immediately from known results about cover times in expanders. For
$k = 1$
follows immediately from known results about cover times in expanders. For
![]() $k\geq 2$
, consider
$k\geq 2$
, consider
![]() $\tilde{k} = \lfloor k/2 \rfloor$
, and recall that
$\tilde{k} = \lfloor k/2 \rfloor$
, and recall that
![]() $t_{\mathsf{mix}}^{(\tilde{k},k)} = \mathcal{O}(t_{\mathsf{mix}} ) = \mathcal{O}(\!\log n )$
by Lemma 4.3. By hypothesis
$t_{\mathsf{mix}}^{(\tilde{k},k)} = \mathcal{O}(t_{\mathsf{mix}} ) = \mathcal{O}(\!\log n )$
by Lemma 4.3. By hypothesis
![]() $m/d_{\mathsf{min}} =\mathcal{O}(n)$
and since the graph is an expander
$m/d_{\mathsf{min}} =\mathcal{O}(n)$
and since the graph is an expander
![]() $t_{\mathsf{rel}}=\mathcal{O}(1 )$
, hence by Corollary 3.3 we have
$t_{\mathsf{rel}}=\mathcal{O}(1 )$
, hence by Corollary 3.3 we have
![]() $t_{\mathsf{cov}}^{(\tilde k)}(\pi )=\mathcal{O}((n/\tilde k) \log n )$
. Thus by Theorem 4.7 we have
$t_{\mathsf{cov}}^{(\tilde k)}(\pi )=\mathcal{O}((n/\tilde k) \log n )$
. Thus by Theorem 4.7 we have
![]() $t_{\mathsf{cov}}^{(k)}= \mathcal{O}((n/k) \log n )$
, proving the upper bound.
$t_{\mathsf{cov}}^{(k)}= \mathcal{O}((n/k) \log n )$
, proving the upper bound.
The lower bound follows by Theorem 3.6 since
![]() $t_{\mathsf{cov}}^{(k)}\geq t_{\mathsf{cov}}^{(k)}(\pi ) =\Omega ((n/k) \log n)$
.
$t_{\mathsf{cov}}^{(k)}\geq t_{\mathsf{cov}}^{(k)}(\pi ) =\Omega ((n/k) \log n)$
.
5.4. The hypercube
The hypercube is not covered by the results in the previous section, since it is not an expander. However, we will show that the same bound on stationary cover times holds nevertheless:
Theorem 5.14.
Let
![]() $G$
be the hypercube with
$G$
be the hypercube with
![]() $n$
vertices, then for any
$n$
vertices, then for any
![]() $k\geq 1$
,
$k\geq 1$
,
Proof. We wish to apply Lemma 3.4. This is applicable since the hypercube is regular and by [Reference Cooper and Frieze13], we have that for any vertex
![]() $v$
,
$v$
,
![]() $ \sum _{t=0}^{t_{\mathsf{rel}}} P_{vv}^t\leq 2 + o(1 )$
and
$ \sum _{t=0}^{t_{\mathsf{rel}}} P_{vv}^t\leq 2 + o(1 )$
and
![]() $t_{\mathsf{rel}} = \mathcal{O}(\!\log n )$
.
$t_{\mathsf{rel}} = \mathcal{O}(\!\log n )$
.
We will also derive the result below in a more systematic way than the original proof [Reference Elsässer and Sauerwald20] using our new characterisations involving partial mixing time and hitting times of large sets.
Theorem 5.15. ([Reference Elsässer and Sauerwald20], Theorem 5.4). For the hypercube with
![]() $n$
vertices,
$n$
vertices,
 $$t_{cov}^{(k)} = \left\{ {\matrix{
{\Theta \left( {{n \over k}\log n} \right)} & {if\,1 \le k \le n/\log \log n,} \cr
{\Theta (\log n\log \log n){\rm{ }}} & {if\,n/\log \log n \le k \le n.} \cr
} } \right.$$
$$t_{cov}^{(k)} = \left\{ {\matrix{
{\Theta \left( {{n \over k}\log n} \right)} & {if\,1 \le k \le n/\log \log n,} \cr
{\Theta (\log n\log \log n){\rm{ }}} & {if\,n/\log \log n \le k \le n.} \cr
} } \right.$$
In order to prove this theorem, we need to bound
![]() $t_{\mathsf{large-hit}}^{ (\alpha,n )}$
from below which is done with the following lemma.
$t_{\mathsf{large-hit}}^{ (\alpha,n )}$
from below which is done with the following lemma.
Lemma 5.16.
For the hypercube with
![]() $n$
vertices and any
$n$
vertices and any
![]() $1\leq \tilde{k}\leq k$
satisfying
$1\leq \tilde{k}\leq k$
satisfying
![]() $\tilde{k} \geq k\cdot e^{-\sqrt{\log n}}\geq 1$
we have
$\tilde{k} \geq k\cdot e^{-\sqrt{\log n}}\geq 1$
we have
Proof of Lemma
5.16. Let
![]() $d$
denotes the dimension of the hypercube with
$d$
denotes the dimension of the hypercube with
![]() $n=2^d$
vertices. Fix the vertex
$n=2^d$
vertices. Fix the vertex
![]() $u=0^{d}$
and consider the set
$u=0^{d}$
and consider the set
![]() $S_u=\{v \in V \,:\, d_H(u,v)\leq d/2 \}$
, so
$S_u=\{v \in V \,:\, d_H(u,v)\leq d/2 \}$
, so
![]() $|S_u| \leq 3n/4$
. Here
$|S_u| \leq 3n/4$
. Here
![]() $d_H$
is the Hamming distance. We will estimate the probability of a random walk leaving
$d_H$
is the Hamming distance. We will estimate the probability of a random walk leaving
![]() $S_u$
in
$S_u$
in
![]() $\ell = (1/100) d \log d$
steps. Recall that a lazy random walk on the hypercube can be considered as performing the following two-step process in each round: (1) Choose one of the
$\ell = (1/100) d \log d$
steps. Recall that a lazy random walk on the hypercube can be considered as performing the following two-step process in each round: (1) Choose one of the
![]() $d$
bits uniformly at random, (2) Independently, set the bit to
$d$
bits uniformly at random, (2) Independently, set the bit to
![]() $\{0,1\}$
uniformly at random.
$\{0,1\}$
uniformly at random.
Let us denote by
![]() $C_{t}$
the set of chosen coordinates, and
$C_{t}$
the set of chosen coordinates, and
![]() $U_{t}$
the set of unchosen coordinates in any of the first
$U_{t}$
the set of unchosen coordinates in any of the first
![]() $t\leq \ell$
steps in the process above. Note that the unchosen coordinates are zero, while the chosen coordinates are in
$t\leq \ell$
steps in the process above. Note that the unchosen coordinates are zero, while the chosen coordinates are in
![]() $\{0,1\}$
independently and uniformly. By linearity of expectations and since
$\{0,1\}$
independently and uniformly. By linearity of expectations and since
![]() $|U_t|$
is non-increasing in
$|U_t|$
is non-increasing in
![]() $t$
, we have
$t$
, we have
where the first inequality is by (1). Using the Method of Bounded Differences [Reference Dubhashi and Panconesi18, Theorem 5.3], we conclude that for any
![]() $t \leq \ell$
,
$t \leq \ell$
,
Next consider the sum of the values at the chosen coordinates
![]() $C_{t}$
at time
$C_{t}$
at time
![]() $t\leq \ell$
, which is given by
$t\leq \ell$
, which is given by
where the
![]() $Y_i \in \{0,1\}$
are independent and uniform variables, representing the coordinates of the random walk. Note that
$Y_i \in \{0,1\}$
are independent and uniform variables, representing the coordinates of the random walk. Note that
![]() ${\mathbb{E}} [Z_t\mid |C_{t}|]=|C_{t}|/2$
, and so Hoeffding’s bound implies
${\mathbb{E}} [Z_t\mid |C_{t}|]=|C_{t}|/2$
, and so Hoeffding’s bound implies
Conditional on the events
![]() $|U_{t}| \geq d^{0.8}$
and
$|U_{t}| \geq d^{0.8}$
and
![]() $Z_t \leq {\mathbb{E}} [Z_t] +2 d^{0.75}$
we have
$Z_t \leq {\mathbb{E}} [Z_t] +2 d^{0.75}$
we have
![]() $Z_t\leq (d-d^{0.8})/2+2d^{0.75}\lt d/2$
, and so the random walk is still in the set
$Z_t\leq (d-d^{0.8})/2+2d^{0.75}\lt d/2$
, and so the random walk is still in the set
![]() $S_u$
at step
$S_u$
at step
![]() $t\leq \ell$
. By the Union bound over the all steps
$t\leq \ell$
. By the Union bound over the all steps
![]() $t=1,\ldots,\ell$
, and (39) and (40), for large
$t=1,\ldots,\ell$
, and (39) and (40), for large
![]() $d$
, these events hold with probability at least
$d$
, these events hold with probability at least
Thus a random walk of length
![]() $\ell$
escapes the set
$\ell$
escapes the set
![]() $S_u$
with probability at most
$S_u$
with probability at most
![]() $e^{-\sqrt{\log n}}$
. Since
$e^{-\sqrt{\log n}}$
. Since
![]() $S_u$
must be escaped to hit a worst-case set with stationary mass at least
$S_u$
must be escaped to hit a worst-case set with stationary mass at least
![]() $1/4$
, it follows that from the definition (16) of
$1/4$
, it follows that from the definition (16) of
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
and monotonicity that for any
$t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
and monotonicity that for any
![]() $\tilde{k} \geq k\cdot e^{-\sqrt{\log n}}\geq 1$
we have
$\tilde{k} \geq k\cdot e^{-\sqrt{\log n}}\geq 1$
we have
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)}\geq \ell$
.
$t_{\mathsf{large-hit}}^{(\tilde{k},k)}\geq \ell$
.
We can now apply our characterisation to find the worst-case cover time of the hypercube.
Proof of Theorem
5.15. We can assume that
![]() $k\geq 2$
by known results for the cover time of the hypercube. Now, observe that Lemma 4.3 and [Reference Levin, Peres and Wilmer42, (6.15)] yield
$k\geq 2$
by known results for the cover time of the hypercube. Now, observe that Lemma 4.3 and [Reference Levin, Peres and Wilmer42, (6.15)] yield
Case (i) [
![]() $2 \leq k \leq n/\log \log n$
]: By Theorem 5.14, for any
$2 \leq k \leq n/\log \log n$
]: By Theorem 5.14, for any
![]() $1 \leq \tilde{k} \leq k$
we have
$1 \leq \tilde{k} \leq k$
we have
Let
![]() $\tilde{k}=k/2$
and then by (41),
$\tilde{k}=k/2$
and then by (41),
![]() $t_{\mathsf{mix}}(\tilde k,k)$
is always at most
$t_{\mathsf{mix}}(\tilde k,k)$
is always at most
![]() $\mathcal{O}(t_{\mathsf{cov}}^{(\tilde{k})}(\pi ) )$
. Hence Theorem 4.7 implies
$\mathcal{O}(t_{\mathsf{cov}}^{(\tilde{k})}(\pi ) )$
. Hence Theorem 4.7 implies
![]() $t_{\mathsf{cov}}^{(k)}= \mathcal{O}((n/k) \log n )$
. The lower bound follows by Theorem 3.6 since
$t_{\mathsf{cov}}^{(k)}= \mathcal{O}((n/k) \log n )$
. The lower bound follows by Theorem 3.6 since
Case (ii) [
![]() $n/ \log \log n \leq k \leq n$
]: If we choose
$n/ \log \log n \leq k \leq n$
]: If we choose
![]() $\tilde{k}=\lfloor \frac{n}{2\log \log n} \rfloor$
, then by monotonicity
$\tilde{k}=\lfloor \frac{n}{2\log \log n} \rfloor$
, then by monotonicity
Also by monotonicity and (41) we have
![]() $t_{\mathsf{mix}}(\tilde{k},k)\leq t_{\mathsf{mix}}(\lfloor k/2 \rfloor,k) = \mathcal{O}(\!\log n \cdot \log \log n )$
thus the results follows from Theorem 4.7.
$t_{\mathsf{mix}}(\tilde{k},k)\leq t_{\mathsf{mix}}(\lfloor k/2 \rfloor,k) = \mathcal{O}(\!\log n \cdot \log \log n )$
thus the results follows from Theorem 4.7.
To prove a matching lower bound, recall that Lemma 5.16 states
Again, by monotonicity, we can assume
![]() $k=n$
and choose
$k=n$
and choose
![]() $\tilde{k} = \lfloor n \exp\!(\! - \sqrt{ \log n})\rfloor \leq k$
, giving
$\tilde{k} = \lfloor n \exp\!(\! - \sqrt{ \log n})\rfloor \leq k$
, giving
by an application of the first bound in Theorem 4.8.
5.5. Higher dimensional tori
The proof of the stationary cover time of higher dimensional tori is similar to the hypercube.
Theorem 5.17.
For
![]() $d$
-dimensional torus
$d$
-dimensional torus
![]() ${\mathbb{T}}_d$
, where
${\mathbb{T}}_d$
, where
![]() $d\geq 3$
, and any
$d\geq 3$
, and any
![]() $1\leq k \leq n$
we have
$1\leq k \leq n$
we have
Proof. For the
![]() $d$
-dimensional torus, where
$d$
-dimensional torus, where
![]() $d\geq 3$
we have
$d\geq 3$
we have
![]() $ \sum _{t=0}^{t_{\mathsf{rel}}} P_{vv}^t= \mathcal{O}(1 )$
by Lemma A.2. Also
$ \sum _{t=0}^{t_{\mathsf{rel}}} P_{vv}^t= \mathcal{O}(1 )$
by Lemma A.2. Also
![]() $t_{\mathsf{rel}} = \mathcal{O}(n^{2/d} )=o(n )$
, see [Reference Aldous and Fill2, Section 5.2]. Thus, we can apply Lemma 3.4.
$t_{\mathsf{rel}} = \mathcal{O}(n^{2/d} )=o(n )$
, see [Reference Aldous and Fill2, Section 5.2]. Thus, we can apply Lemma 3.4.
Using our machinery, we can recover the following result in full quite easily.
Theorem 5.18. ([Reference Ivaskovic, Kosowski, Pajak, Sauerwald, Vollmer and Vallée31]). For the
![]() $d$
-dimensional torus, where
$d$
-dimensional torus, where
![]() $d \geq 3$
is constant:
$d \geq 3$
is constant:
 $$t_{cov}^{(k)} = \left\{ {\matrix{
{\Theta \left( {{n \over k}\cdot\log n} \right)} & {if\,1 \le k \le 2{n^{1 - 2/d}}\log n,} \cr
{\Theta \left( {{n^{2/d}}\cdot{1 \over {\log (k/({n^{1 - 2/d}}\log n))}}} \right){\rm{ }}} & {if\,2{n^{1 - 2/d}}\log n < k \le n.} \cr
} } \right.$$
$$t_{cov}^{(k)} = \left\{ {\matrix{
{\Theta \left( {{n \over k}\cdot\log n} \right)} & {if\,1 \le k \le 2{n^{1 - 2/d}}\log n,} \cr
{\Theta \left( {{n^{2/d}}\cdot{1 \over {\log (k/({n^{1 - 2/d}}\log n))}}} \right){\rm{ }}} & {if\,2{n^{1 - 2/d}}\log n < k \le n.} \cr
} } \right.$$
Proof of Theorem
5.18. As before, we can assume
![]() $k\geq 2$
by known results for the (single walk) cover time of the
$k\geq 2$
by known results for the (single walk) cover time of the
![]() $d$
-dim torus. By Theorem 5.17 and Lemma 5.4, respectively, we have
$d$
-dim torus. By Theorem 5.17 and Lemma 5.4, respectively, we have
Case (i) [
![]() $2 \leq k \leq 2 n^{1-2/d} \log n$
]: For the upper bound, we can choose
$2 \leq k \leq 2 n^{1-2/d} \log n$
]: For the upper bound, we can choose
![]() $\tilde{k} = \lfloor k/2 \rfloor$
, then by Theorem 4.7, the expected stationary cover time by
$\tilde{k} = \lfloor k/2 \rfloor$
, then by Theorem 4.7, the expected stationary cover time by
![]() $k$
walks is
$k$
walks is
![]() $O(n/k \cdot \log n)$
. To obtain a matching lower bound we can simply use
$O(n/k \cdot \log n)$
. To obtain a matching lower bound we can simply use
![]() $t_{\mathsf{cov}}^{(k)}\geq t_{\mathsf{cov}}^{(k)}(\pi )$
.
$t_{\mathsf{cov}}^{(k)}\geq t_{\mathsf{cov}}^{(k)}(\pi )$
.
Case (ii) [
![]() $2n^{1-2/d} \log n \lt k \leq n$
]: Beginning with the upper bound, set
$2n^{1-2/d} \log n \lt k \leq n$
]: Beginning with the upper bound, set
Then inserting this value for
![]() $\tilde k$
into the bounds from (42) gives
$\tilde k$
into the bounds from (42) gives
 \begin{equation*} t_{\mathsf {cov}}^{(\tilde {k})}(\pi ) = \mathcal {O}\!\left ( \frac {n^{2/d}}{\log \frac {k}{n^{1-2/d} \log n} } \right ), \quad \text {and}\quad t_{\mathsf {mix}}^{(\tilde {k},k)} = \mathcal {O}\!\left ( \frac { n^{2/d}}{ \log\!( \frac {k}{n^{1-2/d} \log n} \cdot \frac {1}{\log\!(k/(n^{1-2/d} \log n)) }) } \right ). \end{equation*}
\begin{equation*} t_{\mathsf {cov}}^{(\tilde {k})}(\pi ) = \mathcal {O}\!\left ( \frac {n^{2/d}}{\log \frac {k}{n^{1-2/d} \log n} } \right ), \quad \text {and}\quad t_{\mathsf {mix}}^{(\tilde {k},k)} = \mathcal {O}\!\left ( \frac { n^{2/d}}{ \log\!( \frac {k}{n^{1-2/d} \log n} \cdot \frac {1}{\log\!(k/(n^{1-2/d} \log n)) }) } \right ). \end{equation*}
These bounds are both of the same order and so the upper bound follows from Theorem 4.7.
For the lower bound set
![]() $\tilde k = n^{1-2/d}\log n \leq k/2$
. Then since
$\tilde k = n^{1-2/d}\log n \leq k/2$
. Then since
![]() $n^{1/3}\lt \tilde{k} \leq k$
, by Theorem 4.8,
$n^{1/3}\lt \tilde{k} \leq k$
, by Theorem 4.8,
for some constant
![]() $C\gt 0$
. For
$C\gt 0$
. For
![]() $t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
, it follows from Lemma 4.11 where we fix
$t_{\mathsf{large-hit}}^{(\tilde{k},k)}$
, it follows from Lemma 4.11 where we fix
![]() $u$
to be any vertex and
$u$
to be any vertex and
![]() $S$
to be the complement of the ball of radius
$S$
to be the complement of the ball of radius
![]() $n^{1/d}/10$
around
$n^{1/d}/10$
around
![]() $u$
that
$u$
that
 \begin{equation*} t_{\mathsf {large-hit}}^{(\tilde {k},k)} = \Omega \left ( \frac {n^{2/d}}{ \log\!( k/ \tilde k ) } \right )= \Omega \left ( \frac {n^{2/d}}{ \log \frac { k}{ n^{1-2/d}\log n} } \right ), \end{equation*}
\begin{equation*} t_{\mathsf {large-hit}}^{(\tilde {k},k)} = \Omega \left ( \frac {n^{2/d}}{ \log\!( k/ \tilde k ) } \right )= \Omega \left ( \frac {n^{2/d}}{ \log \frac { k}{ n^{1-2/d}\log n} } \right ), \end{equation*}
hence by (43) we obtain a matching lower bound.
6. Conclusion and open problems
In this work, we derived several new bounds on multiple stationary and worst-case cover times. We also introduced a new quantity called partial mixing time, which extends the definition of mixing time from single random walks to multiple random walks. By means of a
![]() $\min$
–
$\min$
–
![]() $\max$
characterisation, we proved that the partial mixing time connects the stationary and worst-case cover times, leading to tight lower and upper bounds for many graph classes.
$\max$
characterisation, we proved that the partial mixing time connects the stationary and worst-case cover times, leading to tight lower and upper bounds for many graph classes.
In terms of worst-case bounds, Theorem 3.1 implies that for any regular graph
![]() $G$
and any
$G$
and any
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $t_{\mathsf{cov}}^{(k)}(\pi ) = \mathcal{O}\!\left (\left (\frac{n}{k}\right )^2\log ^2 n \right ).$
This bound is tight for the cycle when
$t_{\mathsf{cov}}^{(k)}(\pi ) = \mathcal{O}\!\left (\left (\frac{n}{k}\right )^2\log ^2 n \right ).$
This bound is tight for the cycle when
![]() $k$
is polynomial in
$k$
is polynomial in
![]() $n$
but not for smaller
$n$
but not for smaller
![]() $k$
. We suspect that for any
$k$
. We suspect that for any
![]() $k\geq 1$
the cycle is (asymptotically) the worst-case for
$k\geq 1$
the cycle is (asymptotically) the worst-case for
![]() $t_{\mathsf{cov}}^{(k)}(\pi )$
amongst regular graphs, which suggests
$t_{\mathsf{cov}}^{(k)}(\pi )$
amongst regular graphs, which suggests
![]() $ t_{\mathsf{cov}}^{(k)}(\pi ) = \mathcal{O}\!\left (\left (\frac{n}{k}\right )^2\log ^2 k \right ).$
$ t_{\mathsf{cov}}^{(k)}(\pi ) = \mathcal{O}\!\left (\left (\frac{n}{k}\right )^2\log ^2 k \right ).$
Some of our results have been only proven for the independent stationary case, but it seems plausible they extend to the case where the
![]() $k$
random walks start from the same vertex. For example, extending the bound
$k$
random walks start from the same vertex. For example, extending the bound
![]() $t_{\mathsf{cov}}^{(k)}(\pi ) =\Omega ( (n/k) \log n)$
to this case would be very interesting.
$t_{\mathsf{cov}}^{(k)}(\pi ) =\Omega ( (n/k) \log n)$
to this case would be very interesting.
Although our
![]() $\min$
–
$\min$
–
![]() $\max$
characterisations involving partial mixing time yields tight bounds for many natural graph classes, it would be interesting to establish a general approximation guarantee (or find graph classes that serve as counter-examples). For the former, we believe techniques such as Gaussian Processes and Majorising Measures used in the seminal work of Ding, Lee and Peres [Reference Ding, Lee and Peres17] could be very useful.
$\max$
characterisations involving partial mixing time yields tight bounds for many natural graph classes, it would be interesting to establish a general approximation guarantee (or find graph classes that serve as counter-examples). For the former, we believe techniques such as Gaussian Processes and Majorising Measures used in the seminal work of Ding, Lee and Peres [Reference Ding, Lee and Peres17] could be very useful.
Acknowledgements
All three authors were supported by the ERC Starting Grant 679660 (DYNAMIC MARCH). Nicolás Rivera was supported by ANID FONDECYT grant number 3210805. John Sylvester was also supported by ESPRC grant number EP/T004878/1 while at the University of Glasgow. We thank Jonathan Hermon for some interesting and useful discussions, and Przemysław Gordinowicz for his feedback on an earlier version of this paper.
A. Appendix: Elementary Results
Lemma A.1.
Let
![]() $X$
be a non-negative integer random variable such that
$X$
be a non-negative integer random variable such that
![]() ${\mathbb{E}} [X]\geq b$
and there exists
${\mathbb{E}} [X]\geq b$
and there exists
![]() $c\geq 0$
such that
$c\geq 0$
such that
![]() ${\mathbb{P}} [X\gt \ell c]\leq {\mathbb{P}} [X\gt c]^\ell$
for all integers
${\mathbb{P}} [X\gt \ell c]\leq {\mathbb{P}} [X\gt c]^\ell$
for all integers
![]() $\ell \geq 0$
. Then for any
$\ell \geq 0$
. Then for any
![]() $a\lt c$
$a\lt c$
Proof. Let
![]() $p= {\mathbb{P}} [X\gt a]\geq {\mathbb{P}} [X\gt c]$
as
$p= {\mathbb{P}} [X\gt a]\geq {\mathbb{P}} [X\gt c]$
as
![]() ${\mathbb{P}} [X\gt x]$
is non-increasing in
${\mathbb{P}} [X\gt x]$
is non-increasing in
![]() $x$
. Now we have
$x$
. Now we have
 \begin{equation*}b\leq a+ \sum _{i=a+1}^{c-1}{\mathbb{P}}\left [x\gt i\right ] +c\sum _{\ell =1}^{\infty }{\mathbb{P}}\left [X\gt c\right ]^\ell \leq a + p(c-a) + cp/(1-p). \end{equation*}
\begin{equation*}b\leq a+ \sum _{i=a+1}^{c-1}{\mathbb{P}}\left [x\gt i\right ] +c\sum _{\ell =1}^{\infty }{\mathbb{P}}\left [X\gt c\right ]^\ell \leq a + p(c-a) + cp/(1-p). \end{equation*}
This implies
![]() $(1-p)b\leq a + 2pc$
, rearranging gives the result.
$(1-p)b\leq a + 2pc$
, rearranging gives the result.
A.1. Returns in the torus
The following result is well-known, however we state it for completeness.
Lemma A.2.
For the d-dimensional torus
![]() ${\mathbb{T}}_d$
on
${\mathbb{T}}_d$
on
![]() $n$
vertices and any
$n$
vertices and any
![]() $1\leq t\leq t_{\mathsf{rel}}$
we have
$1\leq t\leq t_{\mathsf{rel}}$
we have
 \begin{equation*}\sum _{i=0}^t P^i_{v,v} = \begin {cases} \Theta (\sqrt {t}) &\text { if } d=1\\[5pt] \Theta (1+ \log t) &\text { if } d=2\\[5pt] \Theta (1) &\text { if } d \geq 3\\[5pt] \end {cases}.\end{equation*}
\begin{equation*}\sum _{i=0}^t P^i_{v,v} = \begin {cases} \Theta (\sqrt {t}) &\text { if } d=1\\[5pt] \Theta (1+ \log t) &\text { if } d=2\\[5pt] \Theta (1) &\text { if } d \geq 3\\[5pt] \end {cases}.\end{equation*}
Proof. We begin with the lower bounds. Let
![]() $Q$
and
$Q$
and
![]() $P$
be the transition matrices of the lazy walk on the
$P$
be the transition matrices of the lazy walk on the
![]() $d$
-dimensional integer lattice
$d$
-dimensional integer lattice
![]() $\mathbb{Z}^d$
and the
$\mathbb{Z}^d$
and the
![]() $d$
-dimensional torus
$d$
-dimensional torus
![]() ${\mathbb{T}}_d$
, respectively. By [Reference Hebisch and Saloff-Coste28, Theorem 5.1 (15)], for each
${\mathbb{T}}_d$
, respectively. By [Reference Hebisch and Saloff-Coste28, Theorem 5.1 (15)], for each
![]() $d\geq 1$
there exist constants
$d\geq 1$
there exist constants
![]() $C\gt 0$
such that for any
$C\gt 0$
such that for any
![]() $t\geq 1$
and
$t\geq 1$
and
![]() $v \in \mathbb{Z}^d$
we have
$v \in \mathbb{Z}^d$
we have
![]() $ Q_{v,v}^t \geq (C/t )^{d/2}$
. The lower bounds for the torus then follow by summation since for any
$ Q_{v,v}^t \geq (C/t )^{d/2}$
. The lower bounds for the torus then follow by summation since for any
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $v\in V({\mathbb{T}}_d)$
we have
$v\in V({\mathbb{T}}_d)$
we have
![]() $ P_{v,v}^t \geq Q_{v,v}^t$
.
$ P_{v,v}^t \geq Q_{v,v}^t$
.
We now prove the three cases for the upper bounds separately.
Case (i) [
![]() $d=1$
, cycle]: For a lazy random walk in the cycle it holds for
$d=1$
, cycle]: For a lazy random walk in the cycle it holds for
![]() $t\geq 1$
that
$t\geq 1$
that
![]() $P_{v,v}^t \leq \frac{1}{n}+ \frac{c}{\sqrt t}$
, for some constant
$P_{v,v}^t \leq \frac{1}{n}+ \frac{c}{\sqrt t}$
, for some constant
![]() $c\gt 0$
[Reference Lyons and Gharan46, Theorem 4.9]. Now, for any
$c\gt 0$
[Reference Lyons and Gharan46, Theorem 4.9]. Now, for any
![]() $C\geq 1$
, and any
$C\geq 1$
, and any
![]() $1\leq t\leq Cn^2$
, it holds for some
$1\leq t\leq Cn^2$
, it holds for some
![]() $c'\gt 0$
that
$c'\gt 0$
that
 \begin{equation*}\sum _{i=0}^tP_{v,v} \leq c' \sqrt {t}+ C(t+1)/n^2 = O(\sqrt {t}).\end{equation*}
\begin{equation*}\sum _{i=0}^tP_{v,v} \leq c' \sqrt {t}+ C(t+1)/n^2 = O(\sqrt {t}).\end{equation*}
Case (ii) [
![]() $d=2$
]: A random walk of length
$d=2$
]: A random walk of length
![]() $t$
in two dimension can be generated as follows; first sample a random integer
$t$
in two dimension can be generated as follows; first sample a random integer
![]() $x$
according to
$x$
according to
![]() $B(t) \sim \operatorname{Bin}( t,1/2 )$
, where
$B(t) \sim \operatorname{Bin}( t,1/2 )$
, where
![]() $x$
is the number of lazy random walk steps the walk takes in the first dimension (so
$x$
is the number of lazy random walk steps the walk takes in the first dimension (so
![]() $t-x$
is the number of lazy random walk steps the walk takes in the second dimension). Hence, if
$t-x$
is the number of lazy random walk steps the walk takes in the second dimension). Hence, if
![]() $Q$
denotes the law of a lazy random walk on a cycle with
$Q$
denotes the law of a lazy random walk on a cycle with
![]() $\sqrt{n}$
vertices, we have
$\sqrt{n}$
vertices, we have
![]() $P ^t_{v,v} = {\mathbb{E}} \left[Q_{v,v}^{B(t)} Q_{v,v}^{t-B(t)}\right].$
Observe that for real functions
$P ^t_{v,v} = {\mathbb{E}} \left[Q_{v,v}^{B(t)} Q_{v,v}^{t-B(t)}\right].$
Observe that for real functions
![]() $f$
and
$f$
and
![]() $g$
, non-increasing and non-decreasing respectively, random variables
$g$
, non-increasing and non-decreasing respectively, random variables
![]() $B$
and
$B$
and
![]() $B'$
, where
$B'$
, where
![]() $B'$
is an independent copy of
$B'$
is an independent copy of
![]() $B$
, we have
$B$
, we have
Note that
![]() $s\to Q_{v,v}^s$
is non-increasing [Reference Levin, Peres and Wilmer42, Exercise 12.5], so
$s\to Q_{v,v}^s$
is non-increasing [Reference Levin, Peres and Wilmer42, Exercise 12.5], so
![]() $s\to Q_{v,v}^{t-s}$
is non-decreasing, hence
$s\to Q_{v,v}^{t-s}$
is non-decreasing, hence
As
![]() $s\to Q_{v,v}^s$
is non-increasing, we have
$s\to Q_{v,v}^s$
is non-increasing, we have
![]() $Q_{v,v}^s \leq Q_{v,v}^{\lfloor t/4 \rfloor }$
for any
$Q_{v,v}^s \leq Q_{v,v}^{\lfloor t/4 \rfloor }$
for any
![]() $s\geq t/4$
. Then, for
$s\geq t/4$
. Then, for
![]() $t\geq 1$
but
$t\geq 1$
but
![]() $t = \mathcal{O}(n)$
, it holds
$t = \mathcal{O}(n)$
, it holds
![]() $Q_{v,v}^{\lfloor t/4 \rfloor } \leq c_1/\sqrt{t}$
for some constant
$Q_{v,v}^{\lfloor t/4 \rfloor } \leq c_1/\sqrt{t}$
for some constant
![]() $c_1\gt 0$
by [Reference Lyons and Gharan46, Theorem 4.9]. Thus, by Hoeffding’s bound,
$c_1\gt 0$
by [Reference Lyons and Gharan46, Theorem 4.9]. Thus, by Hoeffding’s bound,
for some constant
![]() $c_2\gt 0$
. The statement of Case (ii) then follows by summation.
$c_2\gt 0$
. The statement of Case (ii) then follows by summation.
Case (iii) [
![]() $d\geq 3$
]: By [Reference Levin, Peres and Wilmer42, Proposition 10.13] there is a constant
$d\geq 3$
]: By [Reference Levin, Peres and Wilmer42, Proposition 10.13] there is a constant
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() ${\mathbb{E}}_{u} [\tau _v] \leq C \cdot n$
for all
${\mathbb{E}}_{u} [\tau _v] \leq C \cdot n$
for all
![]() $u,v \in V$
. Hence by Markov’s inequality,
$u,v \in V$
. Hence by Markov’s inequality,
Therefore, for
![]() $t = 2 C \cdot n$
, and by averaging over the start vertex,
$t = 2 C \cdot n$
, and by averaging over the start vertex,
 \begin{equation*} 1/2 \leq {\mathbb{P}}_{\pi }\!\left [ \tau _v \leq t \right ] = \frac {{\mathbb{E}}_{\pi } \!\left [ N_{v}^t\right ] }{ {\mathbb{E}}_{\pi } \!\left [ N_{v}^t \, \mid \, N_{v}^t \geq 1\right ] } \leq \frac { t \cdot 1/n}{1/2 \cdot \sum _{i=0}^{t/2} P_{v,v}^i, } \end{equation*}
\begin{equation*} 1/2 \leq {\mathbb{P}}_{\pi }\!\left [ \tau _v \leq t \right ] = \frac {{\mathbb{E}}_{\pi } \!\left [ N_{v}^t\right ] }{ {\mathbb{E}}_{\pi } \!\left [ N_{v}^t \, \mid \, N_{v}^t \geq 1\right ] } \leq \frac { t \cdot 1/n}{1/2 \cdot \sum _{i=0}^{t/2} P_{v,v}^i, } \end{equation*}
and rearranging yields
 \begin{equation*} \sum _{i=0}^{t} P_{v,v}^i \leq 2 \sum _{i=0}^{t/2} P_{v,v}^i \leq 16 C, \end{equation*}
\begin{equation*} \sum _{i=0}^{t} P_{v,v}^i \leq 2 \sum _{i=0}^{t/2} P_{v,v}^i \leq 16 C, \end{equation*}
where the first inequality holds by monotonicity of
![]() $P_{v,v}^i$
in
$P_{v,v}^i$
in
![]() $i \geq 0$
.
$i \geq 0$
.
A.2. Returns in the binary tree
To prove the results for the binary tree we must control the return probabilities of single random walks, we gather the results required for this task here.
Recall that if
![]() $R(x,y)$
is the effective resistance between
$R(x,y)$
is the effective resistance between
![]() $x$
and
$x$
and
![]() $y$
, (see [Reference Levin, Peres and Wilmer42, Section 9.4]), then for any
$y$
, (see [Reference Levin, Peres and Wilmer42, Section 9.4]), then for any
![]() $x,y\in V$
by [Reference Levin, Peres and Wilmer42, Proposition 9.5]:
$x,y\in V$
by [Reference Levin, Peres and Wilmer42, Proposition 9.5]:
Lemma A.3.
Let
![]() $r$
be the root of a binary tree of height
$r$
be the root of a binary tree of height
![]() $h\geq 4$
, and
$h\geq 4$
, and
![]() $\mathcal{L}$
be the set of leaves. Then, for any
$\mathcal{L}$
be the set of leaves. Then, for any
![]() $T\leq n$
,
$T\leq n$
,
![]() $\sum _{t=0}^T P_{r,r}^t\leq 2 + 6 T/n$
. Additionally
$\sum _{t=0}^T P_{r,r}^t\leq 2 + 6 T/n$
. Additionally
![]() ${\mathbb{P}}_{\pi }[\tau _{r}\leq \tau _{\mathcal{L}} ] \leq (8\log n)/n$
.
${\mathbb{P}}_{\pi }[\tau _{r}\leq \tau _{\mathcal{L}} ] \leq (8\log n)/n$
.
Proof. Identify
![]() $\mathcal{L}$
as a single vertex and observe that
$\mathcal{L}$
as a single vertex and observe that
![]() $R(r,\mathcal{L}) = \sum _{i=1}^h(1/2)^i = 1- 1/2^{h+1}$
, thus
$R(r,\mathcal{L}) = \sum _{i=1}^h(1/2)^i = 1- 1/2^{h+1}$
, thus
![]() ${\mathbb{P}}_{r}[\tau _{\mathcal{L}}\lt \tau _r^+ ]\geq 1/2$
. Once the walk hits
${\mathbb{P}}_{r}[\tau _{\mathcal{L}}\lt \tau _r^+ ]\geq 1/2$
. Once the walk hits
![]() $\mathcal{L}$
equation (44) yields
$\mathcal{L}$
equation (44) yields
![]() ${\mathbb{P}}_{\mathcal{L}}[\tau _r\lt \tau _{\mathcal{L}}^+ ] = (2^h(1-1/2^{h+1}) )^{-1}\leq 3/n$
. Let
${\mathbb{P}}_{\mathcal{L}}[\tau _r\lt \tau _{\mathcal{L}}^+ ] = (2^h(1-1/2^{h+1}) )^{-1}\leq 3/n$
. Let
![]() $X_t$
be a random walk on the binary tree starting from vertex
$X_t$
be a random walk on the binary tree starting from vertex
![]() $r$
, i.e.
$r$
, i.e.
![]() $X_0 = r$
, and let
$X_0 = r$
, and let
![]() $Z_t = \sum _{s=0}^t {1_{\{X_s=r\}}}$
denotes the number of times
$Z_t = \sum _{s=0}^t {1_{\{X_s=r\}}}$
denotes the number of times
![]() $X_t$
hits the root up to time
$X_t$
hits the root up to time
![]() $t$
. Define the stopping time
$t$
. Define the stopping time
![]() $L_i$
as the
$L_i$
as the
![]() $i$
-th time the random walk hits some leaf, that is:
$i$
-th time the random walk hits some leaf, that is:
![]() $L_1= \min \{t\geq 0\,:\, X_t \in \mathcal L\}$
, and for
$L_1= \min \{t\geq 0\,:\, X_t \in \mathcal L\}$
, and for
![]() $i\geq 2$
,
$i\geq 2$
,
![]() $L_i=\min \{t\gt L_{i-1}\,:\, X_t \in \mathcal L\}$
. For
$L_i=\min \{t\gt L_{i-1}\,:\, X_t \in \mathcal L\}$
. For
![]() $i\geq 1$
let
$i\geq 1$
let
![]() $C_{i} = \sum _{t=L_i +1}^{L_{i+1}} {1_{\{X_t = r\}}}$
denote the number of visits to the root between times
$C_{i} = \sum _{t=L_i +1}^{L_{i+1}} {1_{\{X_t = r\}}}$
denote the number of visits to the root between times
![]() $L_i$
and
$L_i$
and
![]() $L_{i+1}$
, and also let
$L_{i+1}$
, and also let
![]() $C_0 = \sum _{t=0}^{L_1} {1_{\{X_t=r\}}}$
. Since
$C_0 = \sum _{t=0}^{L_1} {1_{\{X_t=r\}}}$
. Since
![]() $L_i-L_{i-1}\geq 1$
, then have that
$L_i-L_{i-1}\geq 1$
, then have that
 \begin{equation*} \sum _{t=0}^T P_{r,r}^t= {\mathbb{E}}(Z_T)\leq {\mathbb{E}}(C_0)+\sum _{i=1}^T {\mathbb{E}}(C_i).\end{equation*}
\begin{equation*} \sum _{t=0}^T P_{r,r}^t= {\mathbb{E}}(Z_T)\leq {\mathbb{E}}(C_0)+\sum _{i=1}^T {\mathbb{E}}(C_i).\end{equation*}
Now,
![]() ${\mathbb{E}} [C_0]\leq 2$
since
${\mathbb{E}} [C_0]\leq 2$
since
![]() ${\mathbb{P}}_{r}[\tau _{\mathcal{L}}\lt \tau _r^+ ]\geq 1/2$
and
${\mathbb{P}}_{r}[\tau _{\mathcal{L}}\lt \tau _r^+ ]\geq 1/2$
and
![]() ${\mathbb{E}} [C_i|C_i\geq 1]= {\mathbb{E}} [C_0]$
as in the interval
${\mathbb{E}} [C_i|C_i\geq 1]= {\mathbb{E}} [C_0]$
as in the interval
![]() $C_0$
the walk starts from the root. Also for
$C_0$
the walk starts from the root. Also for
![]() $i\geq 1$
,
$i\geq 1$
,
![]() ${\mathbb{P}} [C_i\geq 1]={\mathbb{P}}_{\mathcal{L}}[\tau _r\lt \tau _{\mathcal{L}}^+ ]\leq 3/n$
, and thus
${\mathbb{P}} [C_i\geq 1]={\mathbb{P}}_{\mathcal{L}}[\tau _r\lt \tau _{\mathcal{L}}^+ ]\leq 3/n$
, and thus
concluding that
![]() $\sum _{t=0}^T P_{r,r}^t\leq 2 + 6T/n$
.
$\sum _{t=0}^T P_{r,r}^t\leq 2 + 6T/n$
.
For the second result, let
![]() $v_i$
be a vertex at distance
$v_i$
be a vertex at distance
![]() $0\leq i\leq h$
from the leaves. Since the walk moves up the tree with probability
$0\leq i\leq h$
from the leaves. Since the walk moves up the tree with probability
![]() $1/3$
and down the tree w.p.
$1/3$
and down the tree w.p.
![]() $2/3$
we have
$2/3$
we have
![]() ${\mathbb{P}}_{v_i}\!\left [\tau _r\lt \tau _{\mathcal{L}}\right ] = \frac{2^i-1}{2^h-1}$
, since this is the classical (biased) Gambler’s ruin problem [Reference Levin, Peres and Wilmer42, Section 17.3.1]. It follows that
${\mathbb{P}}_{v_i}\!\left [\tau _r\lt \tau _{\mathcal{L}}\right ] = \frac{2^i-1}{2^h-1}$
, since this is the classical (biased) Gambler’s ruin problem [Reference Levin, Peres and Wilmer42, Section 17.3.1]. It follows that
 \begin{equation*}{\mathbb{P}}_{\pi }\!\left [\tau _r\lt \tau _{\mathcal {L}}\right ] =\sum _{i=1}^h {\mathbb{P}}_{v_i}\!\left [\tau _r\lt \tau _{\mathcal {L}}\right ]\cdot 2^{h-i}\pi (v_i)\leq \sum _{i=1}^h \frac {2^i}{2^h-1}\cdot 2^{h-i}\cdot \frac {3}{2(n-1)} = \frac {3h}{n-1}, \end{equation*}
\begin{equation*}{\mathbb{P}}_{\pi }\!\left [\tau _r\lt \tau _{\mathcal {L}}\right ] =\sum _{i=1}^h {\mathbb{P}}_{v_i}\!\left [\tau _r\lt \tau _{\mathcal {L}}\right ]\cdot 2^{h-i}\pi (v_i)\leq \sum _{i=1}^h \frac {2^i}{2^h-1}\cdot 2^{h-i}\cdot \frac {3}{2(n-1)} = \frac {3h}{n-1}, \end{equation*}
where the last equality holds as
![]() $2^{h+1}-1=n$
(and so
$2^{h+1}-1=n$
(and so
![]() $2^{h}=(n-1)/2$
). Since
$2^{h}=(n-1)/2$
). Since
![]() $h\geq 4$
, the number of vertices is at least 15, and then
$h\geq 4$
, the number of vertices is at least 15, and then
![]() $h = \log _2(n+1) -1\leq 2\log n$
. Finally, since
$h = \log _2(n+1) -1\leq 2\log n$
. Finally, since
![]() $n-1\geq (6/8)n$
, for
$n-1\geq (6/8)n$
, for
![]() $n\geq 8$
, it holds that
$n\geq 8$
, it holds that
![]() ${\mathbb{P}}_{\pi }\!\left [\tau _r\lt \tau _{\mathcal{L}}\right ] \leq \frac{3h}{(n-1)} \leq 8 \log n/n$
.
${\mathbb{P}}_{\pi }\!\left [\tau _r\lt \tau _{\mathcal{L}}\right ] \leq \frac{3h}{(n-1)} \leq 8 \log n/n$
.
Lemma A.4. ([29, eq 8.21]). Let
![]() $u$
be any leaf in the binary tree. Then for any
$u$
be any leaf in the binary tree. Then for any
![]() $t\geq 1$
,
$t\geq 1$
,
![]() $\sum _{i=0}^tP_{u,u}^t = \Theta \! ( 1+\log\!(t)+t/n )$
.
$\sum _{i=0}^tP_{u,u}^t = \Theta \! ( 1+\log\!(t)+t/n )$
.
Lemma A.5.
Let
![]() $\ell \in V(\mathcal{T}_n)$
be a leaf. Then for any vertex
$\ell \in V(\mathcal{T}_n)$
be a leaf. Then for any vertex
![]() $u\in V(\mathcal{T}_n)$
and
$u\in V(\mathcal{T}_n)$
and
![]() $t\geq 0$
we have
$t\geq 0$
we have
![]() $\sum _{i=0}^{t}P_{u,u}^i \leq 6\cdot \sum _{i=0}^{t}P_{\ell,\ell }^i$
.
$\sum _{i=0}^{t}P_{u,u}^i \leq 6\cdot \sum _{i=0}^{t}P_{\ell,\ell }^i$
.
Proof. Clearly, if
![]() $u$
is a leaf itself, then there is nothing to prove. Hence assume that
$u$
is a leaf itself, then there is nothing to prove. Hence assume that
![]() $u$
is an internal node. Note that
$u$
is an internal node. Note that
![]() $\sum _{s=0}^{t} P_{u,u}^s$
is the expected number of visits to
$\sum _{s=0}^{t} P_{u,u}^s$
is the expected number of visits to
![]() $u$
of a random walk of length
$u$
of a random walk of length
![]() $t$
starting from
$t$
starting from
![]() $u$
. Divide the random walk of length
$u$
. Divide the random walk of length
![]() $t$
into two epochs, where the second epochs starts as soon as a leaf in the subtree rooted at
$t$
into two epochs, where the second epochs starts as soon as a leaf in the subtree rooted at
![]() $u$
is visited. We claim that in the first epoch the expected number of visits to
$u$
is visited. We claim that in the first epoch the expected number of visits to
![]() $u$
is constant. To show this we identify all the leaves of the subtree rooted at
$u$
is constant. To show this we identify all the leaves of the subtree rooted at
![]() $u$
as a single vertex
$u$
as a single vertex
![]() $\mathcal L$
, then by equation (44) we have
$\mathcal L$
, then by equation (44) we have
since
![]() $R(u,\mathcal L)=\sum _{i=1}^h(1/2)^i\leq 1$
. Therefore, in expectation we need at most
$R(u,\mathcal L)=\sum _{i=1}^h(1/2)^i\leq 1$
. Therefore, in expectation we need at most
![]() $3$
excursions to reach
$3$
excursions to reach
![]() $\mathcal L$
, therefore the expected number of visits to
$\mathcal L$
, therefore the expected number of visits to
![]() $u$
in the first epoch is at most
$u$
in the first epoch is at most
![]() $3$
. Then, for any leaf
$3$
. Then, for any leaf
![]() $\ell \in \mathcal{L}$
, the expected number of visits to
$\ell \in \mathcal{L}$
, the expected number of visits to
![]() $u$
in the second epoch satisfies
$u$
in the second epoch satisfies
 \begin{equation*} \sum _{s=1}^{t} P_{\ell,u}^{s} \leq 3 \sum _{s=1}^{t} P_{u,\ell }^{s} \leq 3 \sum _{s=0}^{t} P_{\ell,\ell }^{s}, \end{equation*}
\begin{equation*} \sum _{s=1}^{t} P_{\ell,u}^{s} \leq 3 \sum _{s=1}^{t} P_{u,\ell }^{s} \leq 3 \sum _{s=0}^{t} P_{\ell,\ell }^{s}, \end{equation*}
where the first inequality holds by reversibility and the second inequality holds since the expected number of visits to a vertex is maximised if a random walk starts from that vertex. Adding up the expected number of visits from the two epochs yields the claim.