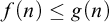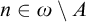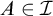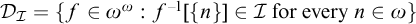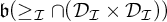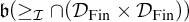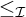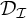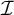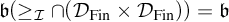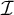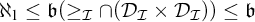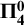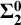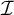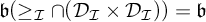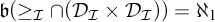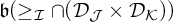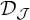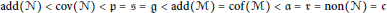5 results
MORE ON YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-16
-
- Article
- Export citation
Infinite dimensional sequential compactness: Sequential compactness based on barriers
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-28
-
- Article
-
- You have access
- HTML
- Export citation
YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1065-1092
- Print publication:
- September 2022
-
- Article
- Export citation
Splitting, Bounding, and Almost Disjointness Can Be Quite Different
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 3 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 502-531
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
SILVER ANTICHAINS
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 April 2015, pp. 503-519
- Print publication:
- June 2015
-
- Article
- Export citation