Article contents
YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER
Published online by Cambridge University Press: 13 September 2021
Abstract
Let 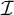 $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on 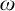 $\omega $
. For
$\omega $
. For 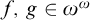 $f,\,g\in \omega ^{\omega }$
we write
$f,\,g\in \omega ^{\omega }$
we write 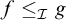 $f \leq _{\mathcal {I}} g$
if
$f \leq _{\mathcal {I}} g$
if 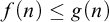 $f(n) \leq g(n)$
for all
$f(n) \leq g(n)$
for all 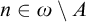 $n\in \omega \setminus A$
with some
$n\in \omega \setminus A$
with some 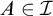 $A\in \mathcal {I}$
. Moreover, we denote
$A\in \mathcal {I}$
. Moreover, we denote 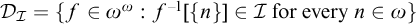 $\mathcal {D}_{\mathcal {I}}=\{f\in \omega ^{\omega }: f^{-1}[\{n\}]\in \mathcal {I} \text { for every } n\in \omega \}$
(in particular,
$\mathcal {D}_{\mathcal {I}}=\{f\in \omega ^{\omega }: f^{-1}[\{n\}]\in \mathcal {I} \text { for every } n\in \omega \}$
(in particular,  $\mathcal {D}_{\mathrm {Fin}}$
denotes the family of all finite-to-one functions).
$\mathcal {D}_{\mathrm {Fin}}$
denotes the family of all finite-to-one functions).
We examine cardinal numbers 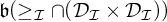 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))$
and
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))$
and 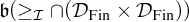 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
describing the smallest sizes of unbounded from below with respect to the order
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}}\times \mathcal {D}_{\mathrm {Fin}}))$
describing the smallest sizes of unbounded from below with respect to the order 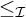 $\leq _{\mathcal {I}}$
sets in
$\leq _{\mathcal {I}}$
sets in  $\mathcal {D}_{\mathrm {Fin}}$
and
$\mathcal {D}_{\mathrm {Fin}}$
and 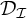 $\mathcal {D}_{\mathcal {I}}$
, respectively. For a maximal ideal
$\mathcal {D}_{\mathcal {I}}$
, respectively. For a maximal ideal 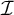 $\mathcal {I}$
, these cardinals were investigated by M. Canjar in connection with coinitial and cofinal subsets of the ultrapowers.
$\mathcal {I}$
, these cardinals were investigated by M. Canjar in connection with coinitial and cofinal subsets of the ultrapowers.
We show that 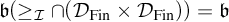 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}} \times \mathcal {D}_{\mathrm {Fin}})) =\mathfrak {b}$
for all ideals
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathrm {Fin}} \times \mathcal {D}_{\mathrm {Fin}})) =\mathfrak {b}$
for all ideals 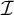 $\mathcal {I}$
with the Baire property and that
$\mathcal {I}$
with the Baire property and that 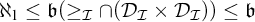 $\aleph _1 \leq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}})) \leq \mathfrak {b}$
for all coanalytic weak P-ideals (this class contains all
$\aleph _1 \leq \mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}})) \leq \mathfrak {b}$
for all coanalytic weak P-ideals (this class contains all 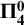 $\bf {\Pi ^0_4}$
ideals). What is more, we give examples of Borel (even
$\bf {\Pi ^0_4}$
ideals). What is more, we give examples of Borel (even 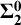 $\bf {\Sigma ^0_2}$
) ideals
$\bf {\Sigma ^0_2}$
) ideals 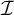 $\mathcal {I}$
with
$\mathcal {I}$
with 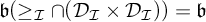 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))=\mathfrak {b}$
as well as with
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))=\mathfrak {b}$
as well as with 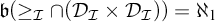 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}})) =\aleph _1$
.
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}})) =\aleph _1$
.
We also study cardinals 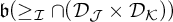 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}} \times \mathcal {D}_{\mathcal {K}}))$
describing the smallest sizes of sets in
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {J}} \times \mathcal {D}_{\mathcal {K}}))$
describing the smallest sizes of sets in 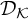 $\mathcal {D}_{\mathcal {K}}$
not bounded from below with respect to the preorder
$\mathcal {D}_{\mathcal {K}}$
not bounded from below with respect to the preorder 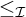 $\leq _{\mathcal {I}}$
by any member of
$\leq _{\mathcal {I}}$
by any member of 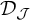 $\mathcal {D}_{\mathcal {J}}\!$
. Our research is partially motivated by the study of ideal-QN-spaces: those cardinals describe the smallest size of a space which is not ideal-QN.
$\mathcal {D}_{\mathcal {J}}\!$
. Our research is partially motivated by the study of ideal-QN-spaces: those cardinals describe the smallest size of a space which is not ideal-QN.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 1
- Cited by



