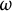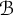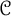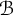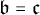1 Introduction
A 2-dimensional version of sequential compactness was first considered by M. Bojańczyk, E. Kopczyński, and S. Toruńczyk in [Reference Bojańczyk, Kopczyński and Toruńczyk3] where they showed that if
![]() $f:[\omega ]^2\to K$
and K is a compact metric space, then there is an infinite set
$f:[\omega ]^2\to K$
and K is a compact metric space, then there is an infinite set
![]() $B\in [\omega ]^\omega $
and
$B\in [\omega ]^\omega $
and
![]() $x\in K$
such that for every open
$x\in K$
such that for every open
![]() $U\ni x$
, there exists
$U\ni x$
, there exists
![]() $m\in \omega $
such that
$m\in \omega $
such that
![]() $f"[B\setminus m]^2\subseteq U$
. In this case, x is said to be the limit of
$f"[B\setminus m]^2\subseteq U$
. In this case, x is said to be the limit of
![]() $f\upharpoonright [B]^2$
. Using this result, they show that every compact metric semigroup has an idempotent that can be defined as the limit of naturally defined
$f\upharpoonright [B]^2$
. Using this result, they show that every compact metric semigroup has an idempotent that can be defined as the limit of naturally defined
![]() $f:[\omega ]^2\to K$
. It is natural to call this property
$f:[\omega ]^2\to K$
. It is natural to call this property
![]() $2$
-dimensional sequential compactness and look for higher-dimensional versions. In fact, the notion of n-sequential compactness was introduced and studied in [Reference Kubiś and Szeptycki19] (called n-Ramsey in their paper) as a natural generalization from the case
$2$
-dimensional sequential compactness and look for higher-dimensional versions. In fact, the notion of n-sequential compactness was introduced and studied in [Reference Kubiś and Szeptycki19] (called n-Ramsey in their paper) as a natural generalization from the case
![]() $n=2$
to all other positive integers n. A space X is said to be n-sequentially compact if for every function
$n=2$
to all other positive integers n. A space X is said to be n-sequentially compact if for every function
![]() $f:[\omega ]^n\to X$
, there is an infinite set
$f:[\omega ]^n\to X$
, there is an infinite set
![]() $M\in [\omega ]^\omega $
and
$M\in [\omega ]^\omega $
and
![]() $x\in X$
such that for every open
$x\in X$
such that for every open
![]() $U\ni x$
, there exists
$U\ni x$
, there exists
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $f"[M\setminus k]^n\subseteq U$
. It was shown in [Reference Kubiś and Szeptycki19] that every n-sequentially compact space is also m-sequentially compact as long as
$f"[M\setminus k]^n\subseteq U$
. It was shown in [Reference Kubiś and Szeptycki19] that every n-sequentially compact space is also m-sequentially compact as long as
![]() $m\leq n$
, and since
$m\leq n$
, and since
![]() $1$
-sequential compactness coincides with the classical notion of sequential compactness, every n-sequentially compact space is also sequentially compact. However, they gave examples of n-sequentially compact spaces that are not
$1$
-sequential compactness coincides with the classical notion of sequential compactness, every n-sequentially compact space is also sequentially compact. However, they gave examples of n-sequentially compact spaces that are not
![]() $(n+1)$
-sequentially compact (assuming CH for
$(n+1)$
-sequentially compact (assuming CH for
![]() $n>1$
) and proved that sequentially compact spaces of character less than
$n>1$
) and proved that sequentially compact spaces of character less than
![]() ${\mathfrak {b}}$
are n-sequentially compact for all
${\mathfrak {b}}$
are n-sequentially compact for all
![]() $n\in \omega $
, among other results. Many of these results were further improved in [Reference Corral, Guzmán and López-Callejas7], where the study of n-sequentially compact spaces was carried on.
$n\in \omega $
, among other results. Many of these results were further improved in [Reference Corral, Guzmán and López-Callejas7], where the study of n-sequentially compact spaces was carried on.
It should be mentioned that a related notion of Ramsey convergence was introduced and studied by H. Knaust in [Reference Knaust15]. Given an array
![]() $\{x_{i,j}:0\leq i<j<\omega \}$
in a space X, it is said that it converges Ramsey-uniformly to a point x in X if there is an infinite set
$\{x_{i,j}:0\leq i<j<\omega \}$
in a space X, it is said that it converges Ramsey-uniformly to a point x in X if there is an infinite set
![]() $M\in [\omega ]^\omega $
such that for every open neighborhood U of x, there is
$M\in [\omega ]^\omega $
such that for every open neighborhood U of x, there is
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $x_{i,j}\in U$
for every
$x_{i,j}\in U$
for every
![]() $i,j\in M$
with
$i,j\in M$
with
![]() $k\leq i<j$
. Knaust also defines a space X to have the Ramsey property if given an array
$k\leq i<j$
. Knaust also defines a space X to have the Ramsey property if given an array
![]() $\{x_{n,m}:n<m<\omega \}$
and a point x in the space X such that
$\{x_{n,m}:n<m<\omega \}$
and a point x in the space X such that
![]() $\lim _{n\to \infty }\lim _{m\to \infty }x_{n,m}=x$
, the array
$\lim _{n\to \infty }\lim _{m\to \infty }x_{n,m}=x$
, the array
![]() $\{x_{n,m}:n<m<\omega \}$
converges Ramsey uniformly to x. He then showed that every Rosenthal compact has the Ramsey property. In the subsequent paper [Reference Knaust16], Knaust showed that some classes of angelic spaces have the Ramsey property, including function spaces
$\{x_{n,m}:n<m<\omega \}$
converges Ramsey uniformly to x. He then showed that every Rosenthal compact has the Ramsey property. In the subsequent paper [Reference Knaust16], Knaust showed that some classes of angelic spaces have the Ramsey property, including function spaces
![]() $C_p(X)$
over quasi-Suslin spaces X.
$C_p(X)$
over quasi-Suslin spaces X.
The purpose of this paper is to extend the notion of sequential compactness to infinite dimensions. This is done using barriers of Nash-Williams [Reference Nash-Williams22], where the notion of “dimension” is captured by the rank of the barrier which can be any countable ordinal. Since the simplest examples of barriers are the families
![]() $[\omega ]^n$
, the notion of “Barrier-sequential compactness” is a natural one.
$[\omega ]^n$
, the notion of “Barrier-sequential compactness” is a natural one.
We start in Section 2 by studying the general theory of barriers and stating many results that are the main tools used in our proofs in later sections.
In Section 3, we study the classes of
![]() $\alpha $
-sequentially compact spaces and prove some basic results. For this definition to make sense, we will show that this property depends mostly on the rank of a given barrier and not on the particular recursive structure of it.
$\alpha $
-sequentially compact spaces and prove some basic results. For this definition to make sense, we will show that this property depends mostly on the rank of a given barrier and not on the particular recursive structure of it.
In Section 4, we show that sequentially compact spaces of small character and compact bisequential spaces are
![]() $\alpha $
-sequentially compact for every
$\alpha $
-sequentially compact for every
![]() $\alpha <\omega _1$
. As a corollary, we obtain that many classical classes of compact spaces are
$\alpha <\omega _1$
. As a corollary, we obtain that many classical classes of compact spaces are
![]() $\alpha $
-sequentially compact for every
$\alpha $
-sequentially compact for every
![]() $\alpha $
. We close the section with some comments on angelic spaces, and we point out that a space constructed in [Reference Kubiś and Szeptycki19] and improved in [Reference Corral, Guzmán and López-Callejas7] is an angelic space that fails to satisfy the Ramsey property, answering a question of Knaust [Reference Knaust15].
$\alpha $
. We close the section with some comments on angelic spaces, and we point out that a space constructed in [Reference Kubiś and Szeptycki19] and improved in [Reference Corral, Guzmán and López-Callejas7] is an angelic space that fails to satisfy the Ramsey property, answering a question of Knaust [Reference Knaust15].
In Section 5, we present the constructions of spaces that are
![]() $\beta $
-sequentially compact but not
$\beta $
-sequentially compact but not
![]() $\alpha $
-sequentially compact for
$\alpha $
-sequentially compact for
![]() $\beta <\alpha $
, under the assumption of
$\beta <\alpha $
, under the assumption of
![]() $\mathfrak {b}=\mathfrak {c}$
. We also analyze further the properties mentioned in Section 3 and their relation to
$\mathfrak {b}=\mathfrak {c}$
. We also analyze further the properties mentioned in Section 3 and their relation to
![]() $\alpha $
-sequential compactness.
$\alpha $
-sequential compactness.
Finally, in Section 6, we define and discuss a number of cardinal invariants associated to these classes of spaces and give some topological applications.
Our terminology and notation is mostly standard. In particular,
![]() ${\mathcal {N}}(x)$
stands for the collection of open neighborhoods of x and for a finite set
${\mathcal {N}}(x)$
stands for the collection of open neighborhoods of x and for a finite set
![]() $\{b_0,\ldots ,b_n\}\in [\omega ]^{<\omega }$
, we will always assume that it is written in increasing order.
$\{b_0,\ldots ,b_n\}\in [\omega ]^{<\omega }$
, we will always assume that it is written in increasing order.
We will be using a number of classical cardinal invariants of the continuum including
![]() ${\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}$
,
${\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}$
,
![]() ${\mathfrak {p}} {\mathfrak {b}}$
,
${\mathfrak {p}} {\mathfrak {b}}$
,
![]() ${\mathfrak {s}}$
,
${\mathfrak {s}}$
,
![]() ${\mathfrak {d}}$
,
${\mathfrak {d}}$
,
![]() ${\mathfrak {r}}$
,
${\mathfrak {r}}$
,
![]() ${\mathfrak {r}}_\sigma $
. We refer the reader to [Reference Blass2] for the background on these cardinals.
${\mathfrak {r}}_\sigma $
. We refer the reader to [Reference Blass2] for the background on these cardinals.
Given an almost disjoint family
![]() ${\mathcal {A}}$
on a countable set N, we define its Franklin space as then the one-point compactification of
${\mathcal {A}}$
on a countable set N, we define its Franklin space as then the one-point compactification of
![]() $\Psi ({\mathcal {A}})$
(i.e.,
$\Psi ({\mathcal {A}})$
(i.e.,
![]() ${\mathcal {F}}({\mathcal {A}})=\Psi ({\mathcal {A}})\cup \{\infty \}$
). Our counterexamples are almost exclusively Franklin spaces. For more on almost disjoint families and
${\mathcal {F}}({\mathcal {A}})=\Psi ({\mathcal {A}})\cup \{\infty \}$
). Our counterexamples are almost exclusively Franklin spaces. For more on almost disjoint families and
![]() $\Psi $
-spaces, see [Reference Hernández-Hernández and Hrušák14].
$\Psi $
-spaces, see [Reference Hernández-Hernández and Hrušák14].
Any other set-theoretic notion and terminology is standard and can be found in [Reference Kunen20], and we refer the reader to [Reference Engelking12] for topological terminology.
2 Barriers and fronts
We now introduce the basic concepts of barriers and fronts on
![]() $[\omega ]^{<\omega }$
. This section is mainly based on [Reference Spiros and Todorčević1] and [Reference Todorčević26], although some results are new or adapted and will be applied in subsequent sections where we will extend the theory of n-sequentially compact spaces by defining the notion of barrier sequential compactness and ultimately
$[\omega ]^{<\omega }$
. This section is mainly based on [Reference Spiros and Todorčević1] and [Reference Todorčević26], although some results are new or adapted and will be applied in subsequent sections where we will extend the theory of n-sequentially compact spaces by defining the notion of barrier sequential compactness and ultimately
![]() $\alpha $
-sequential compactness for all
$\alpha $
-sequential compactness for all
![]() $\alpha <\omega _1$
.
$\alpha <\omega _1$
.
For
![]() ${\mathcal {F}}\subseteq [\omega ]^{<\omega }$
and
${\mathcal {F}}\subseteq [\omega ]^{<\omega }$
and
![]() $M\in [\omega ]^\omega $
, let
$M\in [\omega ]^\omega $
, let
Recall that
![]() $s\sqsubseteq t$
means that t is an end extension of s and
$s\sqsubseteq t$
means that t is an end extension of s and
![]() $s\sqsubset t$
means
$s\sqsubset t$
means
![]() $s\sqsubseteq t$
and
$s\sqsubseteq t$
and
![]() $s\neq t$
.
$s\neq t$
.
Definition 2.1 A family
![]() ${\mathcal {F}}\subseteq [\omega ]^{<\omega }$
is
${\mathcal {F}}\subseteq [\omega ]^{<\omega }$
is
-
• Ramsey: if for every partition
 ${\mathcal {F}}={\mathcal {F}}_0\sqcup \cdots \sqcup {\mathcal {F}}_n$
and for every
${\mathcal {F}}={\mathcal {F}}_0\sqcup \cdots \sqcup {\mathcal {F}}_n$
and for every
 $N\in [\omega ]^\omega $
, there is
$N\in [\omega ]^\omega $
, there is
 $M\in [N]^\omega $
such that all but at most one of the restrictions
$M\in [N]^\omega $
such that all but at most one of the restrictions
 ${\mathcal {F}}_i|M$
are empty.
${\mathcal {F}}_i|M$
are empty. -
• Nash-Williams: if
 $s\sqsubseteq t$
implies
$s\sqsubseteq t$
implies
 $s=t$
for
$s=t$
for
 $s,t\in {\mathcal {F}}$
.
$s,t\in {\mathcal {F}}$
. -
• Sperner: if
 $s\subseteq t$
implies
$s\subseteq t$
implies
 $s=t$
for
$s=t$
for
 $s,t\in {\mathcal {F}}$
.
$s,t\in {\mathcal {F}}$
.
Given a Ramsey family
![]() ${\mathcal {F}}$
, applying the Ramsey property to the partition
${\mathcal {F}}$
, applying the Ramsey property to the partition
![]() ${\mathcal {F}}={\mathcal {F}}_0\cup ({\mathcal {F}}\setminus {\mathcal {F}}_0)$
where
${\mathcal {F}}={\mathcal {F}}_0\cup ({\mathcal {F}}\setminus {\mathcal {F}}_0)$
where
![]() ${\mathcal {F}}_0$
is the set of
${\mathcal {F}}_0$
is the set of
![]() $\subseteq $
-minimal elements in
$\subseteq $
-minimal elements in
![]() ${\mathcal {F}}$
, we get the following:
${\mathcal {F}}$
, we get the following:
Proposition 2.2 If
![]() ${\mathcal {F}}$
is Ramsey, there exists
${\mathcal {F}}$
is Ramsey, there exists
![]() $M\in [\omega ]^\omega $
such that
$M\in [\omega ]^\omega $
such that
![]() ${\mathcal {F}}|M$
is Sperner.
${\mathcal {F}}|M$
is Sperner.
Theorem 2.3 [Reference Nash-Williams22] Every Nash-Williams family is Ramsey.
The previous two results show that (at least if one is willing to pass to an infinite subset) the three concepts of being Ramsey, Nash-Williams, and Sperner are equivalent:
Definition 2.4 A Nash-Williams family
![]() ${\mathcal {F}}$
such that for every
${\mathcal {F}}$
such that for every
![]() $M\in [\omega ]^\omega $
there is an initial segment
$M\in [\omega ]^\omega $
there is an initial segment
![]() $s\sqsubseteq M$
with
$s\sqsubseteq M$
with
![]() $s\in {\mathcal {F}}$
is called a front. If, moreover,
$s\in {\mathcal {F}}$
is called a front. If, moreover,
![]() ${\mathcal {F}}$
is Sperner, we say that
${\mathcal {F}}$
is Sperner, we say that
![]() ${\mathcal {F}}$
is a barrier on
${\mathcal {F}}$
is a barrier on
![]() $\omega $
.
$\omega $
.
The same argument for Proposition 2.2 can be used to show the following facts:
Fact 2.5 If
![]() ${\mathcal {F}}$
is a front on a countable set M, there exists
${\mathcal {F}}$
is a front on a countable set M, there exists
![]() $N\in [M]^\omega $
such that
$N\in [M]^\omega $
such that
![]() ${\mathcal {F}}|N$
is a barrier.
${\mathcal {F}}|N$
is a barrier.
Fact 2.6 For every barrier
![]() ${\mathcal {B}}$
on M, if we partition
${\mathcal {B}}$
on M, if we partition
![]() ${\mathcal {B}}={\mathcal {B}}_0\sqcup \cdots \sqcup {\mathcal {B}}_n$
, there are
${\mathcal {B}}={\mathcal {B}}_0\sqcup \cdots \sqcup {\mathcal {B}}_n$
, there are
![]() $N\in [M]^\omega $
and
$N\in [M]^\omega $
and
![]() $i\leq n$
such that
$i\leq n$
such that
![]() ${\mathcal {B}}_i|N$
is a barrier.
${\mathcal {B}}_i|N$
is a barrier.
Given a barrier
![]() ${\mathcal {B}}$
, let
${\mathcal {B}}$
, let
and
![]() $\rho _{T({\mathcal {B}})}:T({\mathcal {B}})\to \omega _1$
be given by
$\rho _{T({\mathcal {B}})}:T({\mathcal {B}})\to \omega _1$
be given by
where
![]() $\sup \emptyset =0$
. We will omit the subindex
$\sup \emptyset =0$
. We will omit the subindex
![]() $T({\mathcal {B}})$
or replace it by
$T({\mathcal {B}})$
or replace it by
![]() ${\mathcal {B}}$
when no confusion arises, and we will often think of
${\mathcal {B}}$
when no confusion arises, and we will often think of
![]() $T({\mathcal {B}})$
as a subtree of
$T({\mathcal {B}})$
as a subtree of
![]() $\omega ^{<\omega }$
.
$\omega ^{<\omega }$
.
Definition 2.7 For a barrier
![]() ${\mathcal {B}}$
on a countable set M, its rank is defined by
${\mathcal {B}}$
on a countable set M, its rank is defined by
![]() $\rho ({\mathcal {B}}):=\rho _{T({\mathcal {B}})}(\emptyset )$
.
$\rho ({\mathcal {B}}):=\rho _{T({\mathcal {B}})}(\emptyset )$
.
It is worth pointing out that in the definition of
![]() $T({\mathcal {B}})$
, we can replace the condition of being an initial segment of an element
$T({\mathcal {B}})$
, we can replace the condition of being an initial segment of an element
![]() $t\in {\mathcal {B}}$
to being a subset of some
$t\in {\mathcal {B}}$
to being a subset of some
![]() $t'\in {\mathcal {B}}$
due to the following fact.
$t'\in {\mathcal {B}}$
due to the following fact.
Lemma 2.8 If
![]() ${\mathcal {B}}$
is a barrier on
${\mathcal {B}}$
is a barrier on
![]() $\omega $
, then for every
$\omega $
, then for every
![]() $s\in [\omega ]^{<\omega }$
, there exists
$s\in [\omega ]^{<\omega }$
, there exists
![]() $b\in {\mathcal {B}}$
such that
$b\in {\mathcal {B}}$
such that
![]() $s\subseteq b$
if and only if there exists
$s\subseteq b$
if and only if there exists
![]() $b\in {\mathcal {B}}$
such that
$b\in {\mathcal {B}}$
such that
![]() $s\sqsubseteq b$
. In particular,
$s\sqsubseteq b$
. In particular,
![]() $T({\mathcal {B}})=\{s\in [\omega ]^{<\omega }:\exists b\in {\mathcal {B}}\ (s\subseteq b)\}$
.
$T({\mathcal {B}})=\{s\in [\omega ]^{<\omega }:\exists b\in {\mathcal {B}}\ (s\subseteq b)\}$
.
Proof Let
![]() $s\in [\omega ]^{<\omega }$
and
$s\in [\omega ]^{<\omega }$
and
![]() $b\in {\mathcal {B}}$
such that
$b\in {\mathcal {B}}$
such that
![]() $s\subseteq b$
. Define
$s\subseteq b$
. Define
![]() $M=s\cup (\omega \setminus \max (b)+1)$
. We can find
$M=s\cup (\omega \setminus \max (b)+1)$
. We can find
![]() $b'\in {\mathcal {B}}$
such that
$b'\in {\mathcal {B}}$
such that
![]() $b'\sqsubseteq M$
, and hence,
$b'\sqsubseteq M$
, and hence,
![]() $s\sqsubseteq b'$
since otherwise,
$s\sqsubseteq b'$
since otherwise,
![]() $b'\sqsubset s\subseteq b$
would contradict that
$b'\sqsubset s\subseteq b$
would contradict that
![]() ${\mathcal {B}}$
is a
${\mathcal {B}}$
is a
![]() $\subseteq $
-antichain.
$\subseteq $
-antichain.
Given
![]() $a=\{a_0,\ldots ,a_n\}$
and
$a=\{a_0,\ldots ,a_n\}$
and
![]() $b=\{b_0,\ldots ,b_k\}$
with
$b=\{b_0,\ldots ,b_k\}$
with
![]() $k<n$
, denote by
$k<n$
, denote by
![]() $a\ast b$
the end replacement of a with b, defined as follows:
$a\ast b$
the end replacement of a with b, defined as follows:
Lemma 2.9 Let
![]() ${\mathcal {B}}$
be a barrier and
${\mathcal {B}}$
be a barrier and
![]() $a\in {\mathcal {B}}$
enumerated as
$a\in {\mathcal {B}}$
enumerated as
![]() $a=\{a_0,\ldots ,a_{n-1}\}$
. Then, for every
$a=\{a_0,\ldots ,a_{n-1}\}$
. Then, for every
![]() $b\in [\omega \setminus (a_{n-1})]^{<n}$
, there exists
$b\in [\omega \setminus (a_{n-1})]^{<n}$
, there exists
![]() $s\in {\mathcal {B}}$
such that
$s\in {\mathcal {B}}$
such that
![]() $a\ast b\sqsubseteq s$
. In particular,
$a\ast b\sqsubseteq s$
. In particular,
![]() $b\notin {\mathcal {B}}$
.
$b\notin {\mathcal {B}}$
.
Proof Fix
![]() $a=\{a_0,\ldots ,a_{n-1}\}$
and
$a=\{a_0,\ldots ,a_{n-1}\}$
and
![]() $b=\{b_0,\ldots ,b_{k-1}\}$
as in the lemma with
$b=\{b_0,\ldots ,b_{k-1}\}$
as in the lemma with
![]() $k<n$
. We will prove the Lemma by induction on k.
$k<n$
. We will prove the Lemma by induction on k.
If
![]() $k=1$
, then
$k=1$
, then
![]() $b=\{b_0\}$
for some
$b=\{b_0\}$
for some
![]() $b_0\geq a_{n-1}$
. Let
$b_0\geq a_{n-1}$
. Let
![]() $M\in [\omega ]^\omega $
with
$M\in [\omega ]^\omega $
with
![]() $a\ast b\sqsubseteq M$
. There is an
$a\ast b\sqsubseteq M$
. There is an
![]() $s\in {\mathcal {B}}$
such that
$s\in {\mathcal {B}}$
such that
![]() $s\sqsubseteq M$
. Notice that
$s\sqsubseteq M$
. Notice that
![]() $|s|\geq n$
since otherwise,
$|s|\geq n$
since otherwise,
![]() $s\sqsubset a$
would contradict that
$s\sqsubset a$
would contradict that
![]() ${\mathcal {B}}$
is Sperner. Thus,
${\mathcal {B}}$
is Sperner. Thus,
![]() $a\ast b\sqsubseteq s\in {\mathcal {B}}$
.
$a\ast b\sqsubseteq s\in {\mathcal {B}}$
.
Now let
![]() $k>1$
and assume the result is true for
$k>1$
and assume the result is true for
![]() ${k-1}$
. Pick any
${k-1}$
. Pick any
![]() $M\in [\omega ]^\omega $
such that
$M\in [\omega ]^\omega $
such that
![]() $a\ast b\sqsubseteq M$
and let
$a\ast b\sqsubseteq M$
and let
![]() $s\in {\mathcal {B}}$
be an initial segment of M. If
$s\in {\mathcal {B}}$
be an initial segment of M. If
![]() $|s|<n$
, then
$|s|<n$
, then
![]() $s\sqsubseteq \{a_0,\ldots ,a_{n-k-1},b_0,\ldots ,b_{k-2}\}\subseteq \{a_0,\ldots ,a_{n-k},b_0,\ldots ,b_{k-2}\}=a\ast b'$
, where
$s\sqsubseteq \{a_0,\ldots ,a_{n-k-1},b_0,\ldots ,b_{k-2}\}\subseteq \{a_0,\ldots ,a_{n-k},b_0,\ldots ,b_{k-2}\}=a\ast b'$
, where
![]() $b'=\{b_0,\ldots ,b_{k-2}\}$
. Since
$b'=\{b_0,\ldots ,b_{k-2}\}$
. Since
![]() $|b'|=k-1$
, by the inductive hypothesis, we get that
$|b'|=k-1$
, by the inductive hypothesis, we get that
![]() $s\subsetneq a\ast b'\sqsubseteq s'$
for some
$s\subsetneq a\ast b'\sqsubseteq s'$
for some
![]() $s'\in {\mathcal {B}}$
, contradicting that
$s'\in {\mathcal {B}}$
, contradicting that
![]() ${\mathcal {B}}$
is Sperner. Therefore,
${\mathcal {B}}$
is Sperner. Therefore,
![]() $|s|\geq n$
, and hence,
$|s|\geq n$
, and hence,
![]() $a\ast b\sqsubseteq s\in {\mathcal {B}}$
.
$a\ast b\sqsubseteq s\in {\mathcal {B}}$
.
Corollary 2.10 If
![]() ${\mathcal {B}}$
is a barrier on
${\mathcal {B}}$
is a barrier on
![]() $\omega $
of rank
$\omega $
of rank
![]() $k\in \mathbb {N}$
, there exists
$k\in \mathbb {N}$
, there exists
![]() $m\in \omega $
such that
$m\in \omega $
such that
![]() ${\mathcal {B}}|(\omega \setminus m)=[\omega \setminus m]^k$
.
${\mathcal {B}}|(\omega \setminus m)=[\omega \setminus m]^k$
.
Proof Let
![]() ${\mathcal {B}}$
be a barrier of rank k. If there is
${\mathcal {B}}$
be a barrier of rank k. If there is
![]() $a\in {\mathcal {B}}$
of size l, then
$a\in {\mathcal {B}}$
of size l, then
![]() $\rho ({\mathcal {B}})\geq l$
. Thus,
$\rho ({\mathcal {B}})\geq l$
. Thus,
![]() ${\mathcal {B}}\subseteq [\omega ]^{\leq k}$
. It is also easy to see that
${\mathcal {B}}\subseteq [\omega ]^{\leq k}$
. It is also easy to see that
![]() ${\mathcal {B}}\cap [\omega ]^k\neq \emptyset $
since otherwise,
${\mathcal {B}}\cap [\omega ]^k\neq \emptyset $
since otherwise,
![]() $\rho ({\mathcal {B}})<k$
.
$\rho ({\mathcal {B}})<k$
.
Take any
![]() $a\in {\mathcal {B}}\cap [\omega ]^k$
and let
$a\in {\mathcal {B}}\cap [\omega ]^k$
and let
![]() $m=\max (a)+1$
. By Lemma 2.9, if
$m=\max (a)+1$
. By Lemma 2.9, if
![]() $b\in {\mathcal {B}}|(\omega \setminus m)$
has size less than k, we can find
$b\in {\mathcal {B}}|(\omega \setminus m)$
has size less than k, we can find
![]() $s\in {\mathcal {B}}$
such that
$s\in {\mathcal {B}}$
such that
![]() $b'=a\ast b\sqsubseteq s$
. As
$b'=a\ast b\sqsubseteq s$
. As
![]() $|b|<k$
, we have that
$|b|<k$
, we have that
![]() $b\subsetneq b'\sqsubseteq s$
, which contradicts that
$b\subsetneq b'\sqsubseteq s$
, which contradicts that
![]() ${\mathcal {B}}$
is Sperner. Hence,
${\mathcal {B}}$
is Sperner. Hence,
![]() ${\mathcal {B}}|(\omega \setminus m)\subseteq [\omega \setminus m]^k$
.
${\mathcal {B}}|(\omega \setminus m)\subseteq [\omega \setminus m]^k$
.
However, for every
![]() $b\in [\omega \setminus m]^k$
, we can take an infinite set M such that
$b\in [\omega \setminus m]^k$
, we can take an infinite set M such that
![]() $b\sqsubset M$
. Thus, there is an initial segment of M in
$b\sqsubset M$
. Thus, there is an initial segment of M in
![]() ${\mathcal {B}}$
, and from the previous inclusion, it must be the case that
${\mathcal {B}}$
, and from the previous inclusion, it must be the case that
![]() $b\in {\mathcal {B}}$
. Therefore,
$b\in {\mathcal {B}}$
. Therefore,
![]() ${\mathcal {B}}|(\omega \setminus m)=[\omega \setminus m]^k$
.
${\mathcal {B}}|(\omega \setminus m)=[\omega \setminus m]^k$
.
Notation 2.11 Given a family
![]() ${\mathcal {B}}\subseteq [\omega ]^{<\omega }$
,
${\mathcal {B}}\subseteq [\omega ]^{<\omega }$
,
![]() $s\in [\omega ]^{<\omega }$
, and
$s\in [\omega ]^{<\omega }$
, and
![]() $n\in \omega $
, set
$n\in \omega $
, set
-
•
 ${\mathcal {B}}(s)=\{t\in {\mathcal {B}}:s\sqsubseteq t\}$
,
${\mathcal {B}}(s)=\{t\in {\mathcal {B}}:s\sqsubseteq t\}$
, -
•
 ${\mathcal {B}}[s]=\{t\setminus s:t\in {\mathcal {B}}(s)\}$
,
${\mathcal {B}}[s]=\{t\setminus s:t\in {\mathcal {B}}(s)\}$
, -
•
 $s^{\smallfrown {\mathcal {B}}}=\{s\cup t:t\in {\mathcal {B}}\ \land \ \min (t)>\max (s)\}$
,
$s^{\smallfrown {\mathcal {B}}}=\{s\cup t:t\in {\mathcal {B}}\ \land \ \min (t)>\max (s)\}$
, -
•
 ${\mathcal {B}}+n=\{s+n:s\in {\mathcal {B}}\}$
, where
${\mathcal {B}}+n=\{s+n:s\in {\mathcal {B}}\}$
, where
 $s+n=\{m+n:m\in s\}$
.
$s+n=\{m+n:m\in s\}$
.
We write
![]() ${\mathcal {B}}(n)$
,
${\mathcal {B}}(n)$
,
![]() ${\mathcal {B}}[n]$
, and
${\mathcal {B}}[n]$
, and
![]() $n^{\smallfrown {\mathcal {B}}}$
instead of
$n^{\smallfrown {\mathcal {B}}}$
instead of
![]() ${\mathcal {B}}(\{n\})$
,
${\mathcal {B}}(\{n\})$
,
![]() ${\mathcal {B}}[\{n\}]$
, and
${\mathcal {B}}[\{n\}]$
, and
![]() $\{n\}^{\smallfrown {\mathcal {B}}}$
, respectively. Notice that some confusion may arise as
$\{n\}^{\smallfrown {\mathcal {B}}}$
, respectively. Notice that some confusion may arise as
![]() $n=\{0,\ldots ,n-1\}$
, but this notation will not lead to any confusion, as
$n=\{0,\ldots ,n-1\}$
, but this notation will not lead to any confusion, as
![]() ${\mathcal {B}}(n)$
will always be interpreted as
${\mathcal {B}}(n)$
will always be interpreted as
![]() ${\mathcal {B}}(\{n\})$
, and the same for
${\mathcal {B}}(\{n\})$
, and the same for
![]() ${\mathcal {B}}[n]$
and
${\mathcal {B}}[n]$
and
![]() $n^{\smallfrown {\mathcal {B}}}$
. We see that if
$n^{\smallfrown {\mathcal {B}}}$
. We see that if
![]() ${\mathcal {B}}$
is a barrier on M, then
${\mathcal {B}}$
is a barrier on M, then
![]() ${\mathcal {B}}[n]$
is a barrier on
${\mathcal {B}}[n]$
is a barrier on
![]() $M\setminus (n+1)$
. Conversely, if
$M\setminus (n+1)$
. Conversely, if
![]() ${\mathcal {B}}_n$
is a barrier on
${\mathcal {B}}_n$
is a barrier on
![]() $M\setminus (n+1)$
for every
$M\setminus (n+1)$
for every
![]() $n\in M$
, then
$n\in M$
, then
![]() $\bigcup _{n\in M}n^{\smallfrown {\mathcal {B}}}_n$
is a front on M, and there is an infinite set on which its restriction is a barrier. We can now describe a canonical barrier of rank
$\bigcup _{n\in M}n^{\smallfrown {\mathcal {B}}}_n$
is a front on M, and there is an infinite set on which its restriction is a barrier. We can now describe a canonical barrier of rank
![]() $\omega $
: The Schreier barrier
$\omega $
: The Schreier barrier
![]() ${\mathcal {S}}$
is the barrier of rank
${\mathcal {S}}$
is the barrier of rank
![]() $\omega $
such that
$\omega $
such that
![]() $\{0\}\in {\mathcal {S}}$
and
$\{0\}\in {\mathcal {S}}$
and
![]() ${\mathcal {S}}[n]=[\omega \setminus (n+1)]^n$
for every
${\mathcal {S}}[n]=[\omega \setminus (n+1)]^n$
for every
![]() $n>0$
. In other words,
$n>0$
. In other words,
![]() $s\in {\mathcal {S}}$
if and only if
$s\in {\mathcal {S}}$
if and only if
![]() $|s|=\min (s)+1$
.
$|s|=\min (s)+1$
.
Definition 2.12 We define the notion of a uniform barrier by induction on the rank. For
![]() $\alpha =1$
, we declare the unique barrier
$\alpha =1$
, we declare the unique barrier
![]() ${\mathcal {B}}=[\omega ]^1$
as a uniform barrier. Let
${\mathcal {B}}=[\omega ]^1$
as a uniform barrier. Let
![]() ${\mathcal {B}}$
be a barrier on
${\mathcal {B}}$
be a barrier on
![]() $M\in [\omega ]^\omega $
with
$M\in [\omega ]^\omega $
with
![]() $\rho ({\mathcal {B}})=\alpha $
. If
$\rho ({\mathcal {B}})=\alpha $
. If
![]() $\alpha>1$
, we say that
$\alpha>1$
, we say that
![]() ${\mathcal {B}}$
is a uniform barrier if each
${\mathcal {B}}$
is a uniform barrier if each
![]() ${\mathcal {B}}[n]$
is a uniform barrier (on
${\mathcal {B}}[n]$
is a uniform barrier (on
![]() $M\setminus (n+1)$
) and
$M\setminus (n+1)$
) and
-
•
 $\rho _{T({\mathcal {B}})}(\{n\})=\beta $
for every
$\rho _{T({\mathcal {B}})}(\{n\})=\beta $
for every
 $n\in \omega $
if
$n\in \omega $
if
 $\alpha =\beta +1$
or
$\alpha =\beta +1$
or -
•
 $\{\rho _{T({\mathcal {B}})}(\{n\}):n\in \omega \}$
is an increasing sequence with limit
$\{\rho _{T({\mathcal {B}})}(\{n\}):n\in \omega \}$
is an increasing sequence with limit
 $\alpha $
if
$\alpha $
if
 $\alpha $
is limit.
$\alpha $
is limit.
The following result together with Corollary 2.10 shows that all barriers of rank
![]() $\omega $
are somewhere uniform and preserve its rank in such restriction.
$\omega $
are somewhere uniform and preserve its rank in such restriction.
Proposition 2.13 If
![]() ${\mathcal {B}}$
is a barrier of rank
${\mathcal {B}}$
is a barrier of rank
![]() $\omega $
, there exists
$\omega $
, there exists
![]() $M\in [\omega ]^\omega $
such that
$M\in [\omega ]^\omega $
such that
![]() ${\mathcal {B}}|M$
is uniform and has rank
${\mathcal {B}}|M$
is uniform and has rank
![]() $\omega $
.
$\omega $
.
Proof By definition, we can find
![]() $m_i$
such that
$m_i$
such that
![]() $\rho (\{m_i\})\geq i$
for every
$\rho (\{m_i\})\geq i$
for every
![]() $i\in \omega $
. By Corollary 2.10, we can also find
$i\in \omega $
. By Corollary 2.10, we can also find
![]() $k_i$
for every
$k_i$
for every
![]() $i\in \omega $
, such that
$i\in \omega $
, such that
![]() ${\mathcal {B}}[{m_i}]=[\omega \setminus k_i]^{n_i}$
, where
${\mathcal {B}}[{m_i}]=[\omega \setminus k_i]^{n_i}$
, where
![]() $n_i=\rho (\{m_i\})$
. Notice that we can pick
$n_i=\rho (\{m_i\})$
. Notice that we can pick
![]() $\{m_i:i\in \omega \}$
increasing and such that
$\{m_i:i\in \omega \}$
increasing and such that
![]() $m_{i+1}>k_i$
. It is now easy to see that
$m_{i+1}>k_i$
. It is now easy to see that
![]() $M=\{m_i:i\in \omega \}$
works.
$M=\{m_i:i\in \omega \}$
works.
A partial analogue for Proposition 2.13 for any barrier independently of its rank is also true.
Proposition 2.14 [Reference Spiros and Todorčević1] For every barrier
![]() ${\mathcal {B}}$
on
${\mathcal {B}}$
on
![]() $\omega $
, there exists an infinite set
$\omega $
, there exists an infinite set
![]() $M\in [\omega ]^\omega $
such that
$M\in [\omega ]^\omega $
such that
![]() ${\mathcal {B}}|M$
is uniform.
${\mathcal {B}}|M$
is uniform.
By Corollary 2.10, the only uniform barrier of rank
![]() $k\in \omega $
is
$k\in \omega $
is
![]() $[\omega ]^k$
. Thus, Lemma 2.9 states that the sequence of ranks
$[\omega ]^k$
. Thus, Lemma 2.9 states that the sequence of ranks
![]() $\{\rho (\{n\}):n\in \omega \}$
is nondecreasing, and the sequence
$\{\rho (\{n\}):n\in \omega \}$
is nondecreasing, and the sequence
![]() $\{m_i:i\in \omega \}$
can be taken to be the identity in the previous theorem. This shows that the only way to get a nonuniform barrier of rank
$\{m_i:i\in \omega \}$
can be taken to be the identity in the previous theorem. This shows that the only way to get a nonuniform barrier of rank
![]() $\omega $
is by embedding a nonuniform barrier
$\omega $
is by embedding a nonuniform barrier
![]() ${\mathcal {B}}[n]$
on top of
${\mathcal {B}}[n]$
on top of
![]() $\{n\}$
; hence, essentially, every barrier of rank
$\{n\}$
; hence, essentially, every barrier of rank
![]() $\omega $
is uniform. This is as far as we can go since there is a nonuniform barrier
$\omega $
is uniform. This is as far as we can go since there is a nonuniform barrier
![]() ${\mathcal {B}}$
of rank
${\mathcal {B}}$
of rank
![]() $\omega +1$
such that
$\omega +1$
such that
![]() ${\mathcal {B}}[n]$
is uniform for every
${\mathcal {B}}[n]$
is uniform for every
![]() $n\in \omega $
.
$n\in \omega $
.
Example 2.15 There is a nonuniform barrier of rank
![]() $\omega +1$
.
$\omega +1$
.
We define a barrier
![]() ${\mathcal {B}}$
by describing
${\mathcal {B}}$
by describing
![]() ${\mathcal {B}}(n)$
for every
${\mathcal {B}}(n)$
for every
![]() $n\in \omega $
. For every
$n\in \omega $
. For every
![]() $k\in \omega $
, let
$k\in \omega $
, let
![]() ${{\mathcal {S}}_k=\{s\in [\omega ]^{<\omega }:|s|=\min (s)+k\}}$
, (hence, the Schreier barrier is
${{\mathcal {S}}_k=\{s\in [\omega ]^{<\omega }:|s|=\min (s)+k\}}$
, (hence, the Schreier barrier is
![]() ${\mathcal {S}}_1$
). If n is even, define
${\mathcal {S}}_1$
). If n is even, define
![]() ${\mathcal {B}}(n)=n^\smallfrown ({\mathcal {S}}_n+n+1)$
. For n odd, let
${\mathcal {B}}(n)=n^\smallfrown ({\mathcal {S}}_n+n+1)$
. For n odd, let
![]() ${\mathcal {B}}(n)=n^\smallfrown [\omega \setminus (n+1)]^n$
.
${\mathcal {B}}(n)=n^\smallfrown [\omega \setminus (n+1)]^n$
.
Notice that for n even,
![]() $\rho _{T({\mathcal {B}})}(\{n\})=\omega $
, while for n odd,
$\rho _{T({\mathcal {B}})}(\{n\})=\omega $
, while for n odd,
![]() $\rho _{T({\mathcal {B}})}(\{n\})=n+1$
. So
$\rho _{T({\mathcal {B}})}(\{n\})=n+1$
. So
![]() ${\mathcal {B}}$
is not uniform. Moreover,
${\mathcal {B}}$
is not uniform. Moreover,
![]() $\rho ({\mathcal {B}}|E)=\omega +1$
, but
$\rho ({\mathcal {B}}|E)=\omega +1$
, but
![]() $\rho ({\mathcal {B}}|O)=\omega $
, where E is the set of even numbers and O is the set of odd numbers.
$\rho ({\mathcal {B}}|O)=\omega $
, where E is the set of even numbers and O is the set of odd numbers.
It is clear that every infinite subset of
![]() $\omega $
has an initial segment in
$\omega $
has an initial segment in
![]() ${\mathcal {B}}$
and that each
${\mathcal {B}}$
and that each
![]() ${\mathcal {B}}(n)$
is a
${\mathcal {B}}(n)$
is a
![]() $\subseteq $
-antichain. It remains to show that if
$\subseteq $
-antichain. It remains to show that if
![]() $s=\{s_0,\ldots ,s_i\}\in {\mathcal {B}}(n)$
,
$s=\{s_0,\ldots ,s_i\}\in {\mathcal {B}}(n)$
,
![]() $t=\{t_0,\ldots ,t_j\}\in {\mathcal {B}}(m)$
, and
$t=\{t_0,\ldots ,t_j\}\in {\mathcal {B}}(m)$
, and
![]() $n<m$
, then
$n<m$
, then
![]() $t\nsubseteq s$
(the other contention is impossible as
$t\nsubseteq s$
(the other contention is impossible as
![]() $n\in s\setminus t$
).
$n\in s\setminus t$
).
Let us first compute the size of an element
![]() $b\in {\mathcal {B}}$
. Let
$b\in {\mathcal {B}}$
. Let
![]() $b=\{b_0,\ldots ,b_k\}$
. If
$b=\{b_0,\ldots ,b_k\}$
. If
![]() $b_0$
is odd, then
$b_0$
is odd, then
![]() $b\in {\mathcal {B}}(b_0)$
, and it has size
$b\in {\mathcal {B}}(b_0)$
, and it has size
![]() $b_0+1$
. Otherwise,
$b_0+1$
. Otherwise,
![]() $b\in b_0^\smallfrown ({\mathcal {S}}_{b_0}+b_0+1)$
. Let
$b\in b_0^\smallfrown ({\mathcal {S}}_{b_0}+b_0+1)$
. Let
![]() $b'=b\setminus \{b_0\}\in {\mathcal {S}}_{b_0}+b_0+1$
. It is clear that
$b'=b\setminus \{b_0\}\in {\mathcal {S}}_{b_0}+b_0+1$
. It is clear that
![]() $|b'|=|b'-b_0-1|$
, and since
$|b'|=|b'-b_0-1|$
, and since
![]() $(b'-b_0-1)\in {\mathcal {S}}_{b_0}$
and
$(b'-b_0-1)\in {\mathcal {S}}_{b_0}$
and
![]() $\min (b'-b_0-1)=b_1-b_0-1$
, we conclude that
$\min (b'-b_0-1)=b_1-b_0-1$
, we conclude that
![]() $|b'|=|b'-b_0-1|=(b_1-b_0-1)+b_0=b_1-1$
. Therefore,
$|b'|=|b'-b_0-1|=(b_1-b_0-1)+b_0=b_1-1$
. Therefore,
![]() $|b|=b_1$
.
$|b|=b_1$
.
We are now ready to show that s and t are
![]() $\subseteq $
-incomparable. If both n and m are odd, we have that
$\subseteq $
-incomparable. If both n and m are odd, we have that
![]() $|t|=m+1>n+1=|s|$
, and we are done. If both n and m are even, then
$|t|=m+1>n+1=|s|$
, and we are done. If both n and m are even, then
![]() $|s|=s_1$
and
$|s|=s_1$
and
![]() $|t|=t_1$
, but
$|t|=t_1$
, but
![]() $s_0=n\not \in t$
implies that if
$s_0=n\not \in t$
implies that if
![]() $t\subseteq s$
, hence
$t\subseteq s$
, hence
![]() $|s|=s_1\leq t_0<t_1=|t|$
, which is a contradiction.
$|s|=s_1\leq t_0<t_1=|t|$
, which is a contradiction.
Similarly, if n is odd and m is even, we assume that
![]() $t\subseteq s$
yields that
$t\subseteq s$
yields that
![]() $|t|=t_1>t_0\geq s_1\geq s_0+1=|s|$
, a contradiction. Finally, if n is even and m is odd, and if we assume that
$|t|=t_1>t_0\geq s_1\geq s_0+1=|s|$
, a contradiction. Finally, if n is even and m is odd, and if we assume that
![]() $t\subseteq s$
, we reach a contradiction as
$t\subseteq s$
, we reach a contradiction as
![]() $|t|=t_0+1>t_0\geq s_1=|s|$
.
$|t|=t_0+1>t_0\geq s_1=|s|$
.
The persistence of the rank under restriction for a uniform barrier is the key property of the notion of uniformity. We can imitate this behavior by considering a lower bound for the ranks of uniform restrictions of a given barrier
![]() ${\mathcal {B}}$
.
${\mathcal {B}}$
.
Definition 2.16 Given a barrier
![]() ${\mathcal {B}}$
, let
${\mathcal {B}}$
, let
We define the uniform rank of
![]() ${\mathcal {B}}$
as
${\mathcal {B}}$
as
![]() $\rho _u({\mathcal {B}})=\min (\mathrm{spec}({\mathcal {B}}))$
.
$\rho _u({\mathcal {B}})=\min (\mathrm{spec}({\mathcal {B}}))$
.
In [Reference Kubiś and Szeptycki19], it is inductively proved that sequentially compact spaces of character less than
![]() ${\mathfrak {b}}$
are n-sequentially compact for every n. To perform the induction on
${\mathfrak {b}}$
are n-sequentially compact for every n. To perform the induction on
![]() $[\omega ]^{n+1}$
, it is enough to notice that any element of
$[\omega ]^{n+1}$
, it is enough to notice that any element of
![]() $[\omega ]^{n+1}$
has a unique initial segment in
$[\omega ]^{n+1}$
has a unique initial segment in
![]() $[\omega ]^n$
. It is also true that any element in
$[\omega ]^n$
. It is also true that any element in
![]() $[\omega ]^n$
is end-extended by at least one element in
$[\omega ]^n$
is end-extended by at least one element in
![]() $[\omega ]^{n+1}$
. This fact is used to analyze a splitting-like cardinal invariant in [Reference Corral, Guzmán and López-Callejas7] that helps with the construction of n-sequentially compact spaces that fail to be
$[\omega ]^{n+1}$
. This fact is used to analyze a splitting-like cardinal invariant in [Reference Corral, Guzmán and López-Callejas7] that helps with the construction of n-sequentially compact spaces that fail to be
![]() $(n+1)$
-sequentially compact under some assumptions involving this cardinal. Other examples of results that use this fact are Ramsey’s theorem itself and the proof that
$(n+1)$
-sequentially compact under some assumptions involving this cardinal. Other examples of results that use this fact are Ramsey’s theorem itself and the proof that
![]() ${\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}_n={\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}_2=\max \{{\mathfrak {b}},{\mathfrak {s}}\}$
in [Reference Blass2]. In order to obtain analogous results in our framework, we will need a generalization of this fact for barriers of any rank. The statement of Lemma 2.18 below and its proof appear in [Reference Spiros and Todorčević1] in a slightly different way. We add here a proof for completeness.
${\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}_n={\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}_2=\max \{{\mathfrak {b}},{\mathfrak {s}}\}$
in [Reference Blass2]. In order to obtain analogous results in our framework, we will need a generalization of this fact for barriers of any rank. The statement of Lemma 2.18 below and its proof appear in [Reference Spiros and Todorčević1] in a slightly different way. We add here a proof for completeness.
Notation 2.17 Given two families
![]() ${\mathcal {B}},{\mathcal {C}}\subseteq [\omega ]^{<\omega }$
, we denote by
${\mathcal {B}},{\mathcal {C}}\subseteq [\omega ]^{<\omega }$
, we denote by
![]() ${\mathcal {B}}\sqsubseteq {\mathcal {C}}$
if
${\mathcal {B}}\sqsubseteq {\mathcal {C}}$
if
-
•
 $\forall s\in {\mathcal {B}}\ \exists t\in {\mathcal {C}}\ (s\sqsubseteq t)$
,
$\forall s\in {\mathcal {B}}\ \exists t\in {\mathcal {C}}\ (s\sqsubseteq t)$
, -
•
 $\forall t\in {\mathcal {C}}\ \exists s\in {\mathcal {B}}\ (s\sqsubseteq t).$
$\forall t\in {\mathcal {C}}\ \exists s\in {\mathcal {B}}\ (s\sqsubseteq t).$
Lemma 2.18 Given two barriers
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
on a countable set
${\mathcal {C}}$
on a countable set
![]() $N\in [\omega ]^\omega $
, there is an infinite set
$N\in [\omega ]^\omega $
, there is an infinite set
![]() $M\in [N]^\omega $
such that either
$M\in [N]^\omega $
such that either
![]() ${\mathcal {B}}|M\sqsubseteq {\mathcal {C}}|M$
or
${\mathcal {B}}|M\sqsubseteq {\mathcal {C}}|M$
or
![]() ${\mathcal {C}}|M\sqsubseteq {\mathcal {B}}|M$
. Moreover, if
${\mathcal {C}}|M\sqsubseteq {\mathcal {B}}|M$
. Moreover, if
![]() ${\rho ({\mathcal {B}})<\rho ({\mathcal {C}})}$
and
${\rho ({\mathcal {B}})<\rho ({\mathcal {C}})}$
and
![]() ${\mathcal {C}}$
is uniform, then
${\mathcal {C}}$
is uniform, then
![]() ${\mathcal {B}}|M\sqsubseteq {\mathcal {C}}|M$
necessarily holds.
${\mathcal {B}}|M\sqsubseteq {\mathcal {C}}|M$
necessarily holds.
Proof Define
![]() ${\mathcal {B}}_0=\{b\in {\mathcal {B}}:\exists c\in {\mathcal {C}}(b\subseteq c)\}$
. Since
${\mathcal {B}}_0=\{b\in {\mathcal {B}}:\exists c\in {\mathcal {C}}(b\subseteq c)\}$
. Since
![]() ${\mathcal {B}}={\mathcal {B}}_0\cup ({\mathcal {B}}\setminus {\mathcal {B}}_0)$
, we can find, by Nash-Williams theorem, an infinite set
${\mathcal {B}}={\mathcal {B}}_0\cup ({\mathcal {B}}\setminus {\mathcal {B}}_0)$
, we can find, by Nash-Williams theorem, an infinite set
![]() $M\in [N]^\omega $
such that either
$M\in [N]^\omega $
such that either
![]() $({\mathcal {B}}\setminus {\mathcal {B}}_0)|M=\emptyset $
or
$({\mathcal {B}}\setminus {\mathcal {B}}_0)|M=\emptyset $
or
![]() ${\mathcal {B}}_0|M=\emptyset $
. If
${\mathcal {B}}_0|M=\emptyset $
. If
![]() $({\mathcal {B}}\setminus {\mathcal {B}}_0)|M=\emptyset $
, then we are done, as this implies that
$({\mathcal {B}}\setminus {\mathcal {B}}_0)|M=\emptyset $
, then we are done, as this implies that
![]() ${\mathcal {B}}|M\sqsubseteq {\mathcal {C}}|M$
. To see this, notice that for every
${\mathcal {B}}|M\sqsubseteq {\mathcal {C}}|M$
. To see this, notice that for every
![]() $b\in {\mathcal {B}}|M$
( and hence
$b\in {\mathcal {B}}|M$
( and hence
![]() $b\in {\mathcal {B}}_0$
), there is
$b\in {\mathcal {B}}_0$
), there is
![]() $c\in {\mathcal {C}}$
such that
$c\in {\mathcal {C}}$
such that
![]() $b\subseteq c$
, but if we define
$b\subseteq c$
, but if we define
![]() $X=b\cup (M\setminus \max (b))$
, there is also
$X=b\cup (M\setminus \max (b))$
, there is also
![]() $c'\in {\mathcal {C}}$
such that
$c'\in {\mathcal {C}}$
such that
![]() $c'\sqsubseteq X$
. As
$c'\sqsubseteq X$
. As
![]() $b\subseteq c\in {\mathcal {C}}$
, it happens that
$b\subseteq c\in {\mathcal {C}}$
, it happens that
![]() $b\sqsubseteq c'$
and
$b\sqsubseteq c'$
and
![]() $c'\in {\mathcal {C}}|M$
. For
$c'\in {\mathcal {C}}|M$
. For
![]() $c\in {\mathcal {C}}|M$
, we can also find
$c\in {\mathcal {C}}|M$
, we can also find
![]() $b\in {\mathcal {B}}|M$
such that
$b\in {\mathcal {B}}|M$
such that
![]() $b\sqsubseteq c\cup (M\setminus (\max (c)+1))$
. The case where
$b\sqsubseteq c\cup (M\setminus (\max (c)+1))$
. The case where
![]() $c\sqsubset b$
is not possible since
$c\sqsubset b$
is not possible since
![]() $b\in {\mathcal {B}}_0$
, and thus, there is another
$b\in {\mathcal {B}}_0$
, and thus, there is another
![]() $c'\in {\mathcal {C}}|M$
such that
$c'\in {\mathcal {C}}|M$
such that
![]() $b\subseteq c'$
.
$b\subseteq c'$
.
Assume otherwise
![]() ${\mathcal {B}}_0|M=\emptyset $
and define
${\mathcal {B}}_0|M=\emptyset $
and define
![]() ${\mathcal {C}}_0=\{c\in {\mathcal {C}}|M:\exists b\in {\mathcal {B}}|M(c\subseteq b)\}$
. Again, by Nash-Williams theorem, we can find
${\mathcal {C}}_0=\{c\in {\mathcal {C}}|M:\exists b\in {\mathcal {B}}|M(c\subseteq b)\}$
. Again, by Nash-Williams theorem, we can find
![]() $M'\in [M]^\omega $
such that either
$M'\in [M]^\omega $
such that either
![]() ${\mathcal {C}}_0|M'=\emptyset $
or
${\mathcal {C}}_0|M'=\emptyset $
or
![]() $({\mathcal {C}}\setminus {\mathcal {C}}_0)|M'=\emptyset $
. The case
$({\mathcal {C}}\setminus {\mathcal {C}}_0)|M'=\emptyset $
. The case
![]() ${\mathcal {C}}_0|M'=\emptyset $
is impossible since we can find
${\mathcal {C}}_0|M'=\emptyset $
is impossible since we can find
![]() $b\in {\mathcal {B}}|M'\subseteq {\mathcal {B}}|M$
and
$b\in {\mathcal {B}}|M'\subseteq {\mathcal {B}}|M$
and
![]() $c\in {\mathcal {C}}|M'$
such that
$c\in {\mathcal {C}}|M'$
such that
![]() $b,c\sqsubseteq M'$
and then either
$b,c\sqsubseteq M'$
and then either
![]() $b\subseteq c$
or
$b\subseteq c$
or
![]() $c\subseteq b$
contradicting the choices of M and
$c\subseteq b$
contradicting the choices of M and
![]() $M'$
. Thus,
$M'$
. Thus,
![]() $({\mathcal {C}}\setminus {\mathcal {C}}_0)|M'=\emptyset $
, and as in the previous case, we get that
$({\mathcal {C}}\setminus {\mathcal {C}}_0)|M'=\emptyset $
, and as in the previous case, we get that
![]() ${\mathcal {C}}|M'\sqsubseteq {\mathcal {B}}|M'$
.
${\mathcal {C}}|M'\sqsubseteq {\mathcal {B}}|M'$
.
For the last assertion of the statement, notice that if
![]() ${\mathcal {C}}|M\sqsubseteq {\mathcal {B}}|M$
, then
${\mathcal {C}}|M\sqsubseteq {\mathcal {B}}|M$
, then
![]() $T({\mathcal {C}}|M)\subseteq T({\mathcal {B}}|M)$
. In particular,
$T({\mathcal {C}}|M)\subseteq T({\mathcal {B}}|M)$
. In particular,
which finishes the proof.
The previous lemma tells us that we can define a preorder on the family of all barriers on
![]() $\omega $
by defining
$\omega $
by defining
![]() ${\mathcal {B}}\leq {\mathcal {C}}$
if there is an infinite set M such that
${\mathcal {B}}\leq {\mathcal {C}}$
if there is an infinite set M such that
![]() ${\mathcal {B}}|M\sqsubseteq {\mathcal {C}}|M$
. One may be tempted to say that the partial order defined by identifying
${\mathcal {B}}|M\sqsubseteq {\mathcal {C}}|M$
. One may be tempted to say that the partial order defined by identifying
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
if
${\mathcal {C}}$
if
![]() ${\mathcal {B}}\leq {\mathcal {C}}$
and
${\mathcal {B}}\leq {\mathcal {C}}$
and
![]() ${\mathcal {C}}\leq {\mathcal {B}}$
collapses to
${\mathcal {C}}\leq {\mathcal {B}}$
collapses to
![]() $\omega _1$
when restricted to the family of uniform barriers; that is,
$\omega _1$
when restricted to the family of uniform barriers; that is,
![]() ${\mathcal {B}}\leq {\mathcal {C}}$
if and only if
${\mathcal {B}}\leq {\mathcal {C}}$
if and only if
![]() $\rho ({\mathcal {B}})\leq \rho ({\mathcal {C}})$
. However, the unpleasant fact about this is that for two barriers
$\rho ({\mathcal {B}})\leq \rho ({\mathcal {C}})$
. However, the unpleasant fact about this is that for two barriers
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
of the same rank, it is not always true that
${\mathcal {C}}$
of the same rank, it is not always true that
![]() ${\mathcal {B}}\leq {\mathcal {C}}$
and
${\mathcal {B}}\leq {\mathcal {C}}$
and
![]() ${\mathcal {C}}\leq {\mathcal {B}}$
. For example, if
${\mathcal {C}}\leq {\mathcal {B}}$
. For example, if
![]() ${\mathcal {B}}$
is the Schreier barrier and
${\mathcal {B}}$
is the Schreier barrier and
![]() ${\mathcal {C}}$
is any uniform barrier defined such that
${\mathcal {C}}$
is any uniform barrier defined such that
![]() $\rho _{T({\mathcal {C}})}(\{n\})=f(n)$
for an increasing function
$\rho _{T({\mathcal {C}})}(\{n\})=f(n)$
for an increasing function
![]() $f\in \omega ^\omega $
that is strictly bigger that the identity, then
$f\in \omega ^\omega $
that is strictly bigger that the identity, then
![]() ${\mathcal {C}}\nleq {\mathcal {B}}$
. Notice that any uniform barrier
${\mathcal {C}}\nleq {\mathcal {B}}$
. Notice that any uniform barrier
![]() ${\mathcal {B}}$
of rank
${\mathcal {B}}$
of rank
![]() $\omega $
is completely determined by a function
$\omega $
is completely determined by a function
![]() $f\in \omega ^\omega $
that encodes the ranks of the first level on
$f\in \omega ^\omega $
that encodes the ranks of the first level on
![]() $T({\mathcal {B}})$
. A more complex but naturally defined coding of the ranks of the successors of any element
$T({\mathcal {B}})$
. A more complex but naturally defined coding of the ranks of the successors of any element
![]() $s\in T({\mathcal {B}})$
also determines completely the structure of any barrier
$s\in T({\mathcal {B}})$
also determines completely the structure of any barrier
![]() ${\mathcal {B}}$
.
${\mathcal {B}}$
.
We will see now that this function is the only obstruction and that, if one is willing to compress some finite intervals of
![]() $\omega $
into points, we can define a weaker relation between barriers that depends only on their ranks and extends
$\omega $
into points, we can define a weaker relation between barriers that depends only on their ranks and extends
![]() $\leq $
. This will allow us to prove, in some cases, that a property of barriers holds for all barriers of a given rank
$\leq $
. This will allow us to prove, in some cases, that a property of barriers holds for all barriers of a given rank
![]() $\alpha $
(in particular, a space being “
$\alpha $
(in particular, a space being “
![]() ${\mathcal {B}}$
-sequentially compact”) if and only if it holds for some single uniform barrier of the same rank (e.g., Corollary 3.5).
${\mathcal {B}}$
-sequentially compact”) if and only if it holds for some single uniform barrier of the same rank (e.g., Corollary 3.5).
Definition 2.19 Given two barriers
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
on a countable set M, we write
${\mathcal {C}}$
on a countable set M, we write
![]() ${\mathcal {C}}\preceq {\mathcal {B}}$
if there is a finite-to-one, nondecreasing function
${\mathcal {C}}\preceq {\mathcal {B}}$
if there is a finite-to-one, nondecreasing function
![]() $f\in \omega ^\omega $
such that for every infinite subset
$f\in \omega ^\omega $
such that for every infinite subset
![]() $M'\in [M]^\omega $
, there exists
$M'\in [M]^\omega $
, there exists
![]() $N\in [M']^\omega $
so that
$N\in [M']^\omega $
so that
![]() $f\upharpoonright N$
is one-to-one and
$f\upharpoonright N$
is one-to-one and
-
•
 $\forall b\in ({\mathcal {B}}|N)\ \exists c\in {\mathcal {C}}\ (c\sqsubseteq f[b])$
.
$\forall b\in ({\mathcal {B}}|N)\ \exists c\in {\mathcal {C}}\ (c\sqsubseteq f[b])$
.
Notice that if
![]() ${\mathcal {B}}$
is uniform and
${\mathcal {B}}$
is uniform and
![]() $\rho ({\mathcal {C}})<\rho ({\mathcal {B}})$
, then
$\rho ({\mathcal {C}})<\rho ({\mathcal {B}})$
, then
![]() ${\mathcal {C}}\preceq {\mathcal {B}}$
with f being the identity map, since
${\mathcal {C}}\preceq {\mathcal {B}}$
with f being the identity map, since
![]() ${\mathcal {C}}|M\leq {\mathcal {B}}|M$
for every restriction to an infinite set M. The condition that
${\mathcal {C}}|M\leq {\mathcal {B}}|M$
for every restriction to an infinite set M. The condition that
![]() $f\upharpoonright N$
is one-to-one is superfluous, as we can always shrink N in order to get this property, but it will be convenient to add this to the definition to avoid saying it explicitly each time we use the preorder
$f\upharpoonright N$
is one-to-one is superfluous, as we can always shrink N in order to get this property, but it will be convenient to add this to the definition to avoid saying it explicitly each time we use the preorder
![]() $\preceq $
.
$\preceq $
.
Having said this, it is clear that the relation
![]() $\preceq $
is transitive; that is, if
$\preceq $
is transitive; that is, if
![]() ${\mathcal {C}}\preceq {\mathcal {B}}$
and
${\mathcal {C}}\preceq {\mathcal {B}}$
and
![]() ${\mathcal {D}}\preceq {\mathcal {C}}$
is witnessed by f and g, respectively, then
${\mathcal {D}}\preceq {\mathcal {C}}$
is witnessed by f and g, respectively, then
![]() ${\mathcal {D}}\preceq {\mathcal {B}}$
, and it is witnessed by
${\mathcal {D}}\preceq {\mathcal {B}}$
, and it is witnessed by
![]() $g\circ f$
.
$g\circ f$
.
Proposition 2.20 If
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
are two barriers in
${\mathcal {C}}$
are two barriers in
![]() $\omega $
,
$\omega $
,
![]() ${\mathcal {B}}$
is uniform, and
${\mathcal {B}}$
is uniform, and
![]() $\rho ({\mathcal {B}})\geq \rho ({\mathcal {C}})$
, then
$\rho ({\mathcal {B}})\geq \rho ({\mathcal {C}})$
, then
![]() ${\mathcal {C}}\preceq {\mathcal {B}}$
.
${\mathcal {C}}\preceq {\mathcal {B}}$
.
Proof Let us alternately define two sequences
![]() $\{a_i:i\in \omega \}$
and
$\{a_i:i\in \omega \}$
and
![]() $\{b_i:i\in \omega \}$
such that
$\{b_i:i\in \omega \}$
such that
![]() $a_i<b_i<a_{i+1}$
for every
$a_i<b_i<a_{i+1}$
for every
![]() $i\in \omega $
. We will also denote by
$i\in \omega $
. We will also denote by
![]() $\{k_i:i\in \omega \}$
the increasing sequence defined by these two sequences; that is,
$\{k_i:i\in \omega \}$
the increasing sequence defined by these two sequences; that is,
![]() $k_{2i}=a_i$
and
$k_{2i}=a_i$
and
![]() $k_{2i+1}=b_i$
. We will also simultaneously define
$k_{2i+1}=b_i$
. We will also simultaneously define
![]() $f\in \omega ^\omega $
which is completely determined by the sequence
$f\in \omega ^\omega $
which is completely determined by the sequence
![]() $\{k_i:i\in \omega \}$
as follows:
$\{k_i:i\in \omega \}$
as follows:
![]() $f\upharpoonright [0,k_0)=0$
and
$f\upharpoonright [0,k_0)=0$
and
![]() $f(n)=i$
if and only if
$f(n)=i$
if and only if
![]() $n\in [k_i,k_{i+1})$
. We shall show that f satisfies the definition of
$n\in [k_i,k_{i+1})$
. We shall show that f satisfies the definition of
![]() ${\mathcal {C}}\preceq {\mathcal {B}}$
. To save notation, let us write
${\mathcal {C}}\preceq {\mathcal {B}}$
. To save notation, let us write
![]() $\rho _{\mathcal {B}}$
and
$\rho _{\mathcal {B}}$
and
![]() $\rho _{\mathcal {C}}$
instead of
$\rho _{\mathcal {C}}$
instead of
![]() $\rho _{T({\mathcal {B}})}$
and
$\rho _{T({\mathcal {B}})}$
and
![]() $\rho _{T({\mathcal {C}})}$
, respectively. Also, given
$\rho _{T({\mathcal {C}})}$
, respectively. Also, given
![]() $s\in [\omega ]^\omega \setminus T({\mathcal {C}})$
, we will define
$s\in [\omega ]^\omega \setminus T({\mathcal {C}})$
, we will define
![]() $\rho _{\mathcal {C}}(s)=-1$
so that we can talk about the rank of s even if s is not in
$\rho _{\mathcal {C}}(s)=-1$
so that we can talk about the rank of s even if s is not in
![]() $T({\mathcal {C}})$
.
$T({\mathcal {C}})$
.
Step 0:
Since
![]() $\rho _{\mathcal {B}}(\emptyset )\geq \rho _{\mathcal {C}}(\emptyset )$
, there are
$\rho _{\mathcal {B}}(\emptyset )\geq \rho _{\mathcal {C}}(\emptyset )$
, there are
![]() $a_0<b_0<\omega $
such that
$a_0<b_0<\omega $
such that
![]() $\rho _{\mathcal {B}}(\{a_0\})\geq \rho _{\mathcal {C}}(\{0\})$
and
$\rho _{\mathcal {B}}(\{a_0\})\geq \rho _{\mathcal {C}}(\{0\})$
and
![]() $\rho _{\mathcal {B}}(\{b_0\})\geq \rho _{\mathcal {C}}(\{1\})$
.
$\rho _{\mathcal {B}}(\{b_0\})\geq \rho _{\mathcal {C}}(\{1\})$
.
Now assume we have defined
![]() $\{a_i:i\leq n\}$
and
$\{a_i:i\leq n\}$
and
![]() $\{b_i:i\leq n\}$
.
$\{b_i:i\leq n\}$
.
Step a:
Inductive hypothesis at n:
Let us call
We will ensure that the following inductive hypothesis will hold throughout the construction: Given
![]() $s\in S_a(n)$
,
$s\in S_a(n)$
,
-
ϕ a (n, s)
 $\equiv \rho _{\mathcal {B}}(s)\geq \rho _{\mathcal {C}}(f[s])$
$\equiv \rho _{\mathcal {B}}(s)\geq \rho _{\mathcal {C}}(f[s])$
-
ψ a (n, s)
 $\equiv $
if
$\equiv $
if
 $j\geq a_n$
, then
$j\geq a_n$
, then
 $\rho _{\mathcal {B}}(s\cup \{j\})\geq \rho _{\mathcal {C}}(f[s\cup \{2n\}])$
.
$\rho _{\mathcal {B}}(s\cup \{j\})\geq \rho _{\mathcal {C}}(f[s\cup \{2n\}])$
.
We will also write
![]() $\phi _a(n)$
as a shorthand for
$\phi _a(n)$
as a shorthand for
![]() $\forall s\in S_a(n)\phi _a(n,s)$
and
$\forall s\in S_a(n)\phi _a(n,s)$
and
![]() $\psi _a(n)$
as a shorthand for
$\psi _a(n)$
as a shorthand for
![]() $\forall s\in S_a(n)\psi _a(n,s)$
. It is worth pointing out that
$\forall s\in S_a(n)\psi _a(n,s)$
. It is worth pointing out that
![]() $S_a(n)$
,
$S_a(n)$
,
![]() $\phi _a(n,s)$
and
$\phi _a(n,s)$
and
![]() $\psi _a(n,s)$
do not mention
$\psi _a(n,s)$
do not mention
![]() $b_n$
. Note that if
$b_n$
. Note that if
![]() $j\geq a_0$
, we have that
$j\geq a_0$
, we have that
![]() $\rho _{\mathcal {B}}(\{j\})\geq \rho _{\mathcal {B}}(\{a_0\})\geq \rho _{\mathcal {C}}(\{0\})$
as
$\rho _{\mathcal {B}}(\{j\})\geq \rho _{\mathcal {B}}(\{a_0\})\geq \rho _{\mathcal {C}}(\{0\})$
as
![]() ${\mathcal {B}}$
is uniform. Thus,
${\mathcal {B}}$
is uniform. Thus,
![]() $\psi _a(0)$
is satisfied, and
$\psi _a(0)$
is satisfied, and
![]() $\phi _a(0)$
is vacuously satisfied too (here,
$\phi _a(0)$
is vacuously satisfied too (here,
![]() $S_a(0)=\{\emptyset \}$
).
$S_a(0)=\{\emptyset \}$
).
Construction of a n+1:
We need to take care of all
![]() $s\in S_a(n+1)$
(note that this set is well-defined since it only depends on
$s\in S_a(n+1)$
(note that this set is well-defined since it only depends on
![]() $\{a_i,b_i:i\leq n\}$
).
$\{a_i,b_i:i\leq n\}$
).
First, consider
![]() $s\in S_a(n)$
. By
$s\in S_a(n)$
. By
![]() $\phi _a(n,s)$
, we have that
$\phi _a(n,s)$
, we have that
![]() $\rho _{\mathcal {B}}(s)\geq \rho _{\mathcal {C}}(f[s])$
, and thus, we can find
$\rho _{\mathcal {B}}(s)\geq \rho _{\mathcal {C}}(f[s])$
, and thus, we can find
![]() $m_s^a$
such that
$m_s^a$
such that
-
(⋆1 a )
 $\rho _{\mathcal {B}}(s\cup \{m\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+2\})$
for every
$\rho _{\mathcal {B}}(s\cup \{m\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+2\})$
for every
 $m\geq m_s^a$
.
$m\geq m_s^a$
.
Otherwise,
![]() $s\in S_a(n+1)\setminus S_a(n)$
, and we can write
$s\in S_a(n+1)\setminus S_a(n)$
, and we can write
![]() $s'=s\setminus \{j\}$
, where
$s'=s\setminus \{j\}$
, where
![]() $j=\max (s)\geq a_n$
and
$j=\max (s)\geq a_n$
and
![]() $s'\in S_a(n)$
. Then, we know that
$s'\in S_a(n)$
. Then, we know that
![]() $\rho _{\mathcal {B}}(s'\cup \{j\})\geq \rho _{\mathcal {C}}(f[s']\cup \{2n\})$
by
$\rho _{\mathcal {B}}(s'\cup \{j\})\geq \rho _{\mathcal {C}}(f[s']\cup \{2n\})$
by
![]() $\psi _a(n,s)$
. Since
$\psi _a(n,s)$
. Since
![]() $j\in [a_n,b_n)$
, we have that
$j\in [a_n,b_n)$
, we have that
![]() $f(j)=2n$
. Thus,
$f(j)=2n$
. Thus,
-
(*a)
 $\rho _{\mathcal {B}}(s)=\rho _{\mathcal {B}}(s'\cup \{ j\})\geq \rho _{\mathcal {C}}(f[s']\cup \{f(j)\})=\rho _{\mathcal {C}}(f[s'\cup \{j\}])=\rho _{\mathcal {C}}(f[s]).$
$\rho _{\mathcal {B}}(s)=\rho _{\mathcal {B}}(s'\cup \{ j\})\geq \rho _{\mathcal {C}}(f[s']\cup \{f(j)\})=\rho _{\mathcal {C}}(f[s'\cup \{j\}])=\rho _{\mathcal {C}}(f[s]).$
Then, there is
![]() $m_s^a\in \omega $
such that
$m_s^a\in \omega $
such that
![]() $\rho _{\mathcal {B}}(s\cup \{m_s^a\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+2\})$
. Since
$\rho _{\mathcal {B}}(s\cup \{m_s^a\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+2\})$
. Since
![]() ${\mathcal {B}}$
is uniform,
${\mathcal {B}}$
is uniform,
-
(⋆2 a )
 $\rho _{\mathcal {B}}(s\cup \{m\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+2\})$
for every
$\rho _{\mathcal {B}}(s\cup \{m\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+2\})$
for every
 $m\geq m_s^a$
.
$m\geq m_s^a$
.
Finally, define
Inductive hypothesis for n + 1:
We want to see that
![]() $\phi _a(n+1)$
and
$\phi _a(n+1)$
and
![]() $\psi _a(n+1)$
hold. Let
$\psi _a(n+1)$
hold. Let
![]() $s\in S_a(n+1)$
. If
$s\in S_a(n+1)$
. If
![]() ${s\in S_a(n)}$
, then
${s\in S_a(n)}$
, then
![]() $\phi _a(n+1,s)$
follows from
$\phi _a(n+1,s)$
follows from
![]() $\phi _a(n,s)$
. In consequence, we can assume that
$\phi _a(n,s)$
. In consequence, we can assume that
![]() ${s\in S_a(n+1)\setminus S_a(n)}$
and let
${s\in S_a(n+1)\setminus S_a(n)}$
and let
![]() $s'=s\setminus \{j\}$
, where
$s'=s\setminus \{j\}$
, where
![]() $j=\max (s)$
. Hence, by
$j=\max (s)$
. Hence, by
![]() $(\ast ^a)$
, we have that
$(\ast ^a)$
, we have that
![]() $\rho _{{\mathcal {B}}}(s)\geq \rho _{{\mathcal {C}}}(f[s])$
, which means that
$\rho _{{\mathcal {B}}}(s)\geq \rho _{{\mathcal {C}}}(f[s])$
, which means that
![]() $\phi _n(n+1,s)$
holds and, consequently,
$\phi _n(n+1,s)$
holds and, consequently,
![]() $\phi _a(n+1)$
does.
$\phi _a(n+1)$
does.
Now let us see that
![]() $\psi _a(n+1)$
is also true. Let
$\psi _a(n+1)$
is also true. Let
![]() $s\in S_a(n+1)$
and
$s\in S_a(n+1)$
and
![]() $j\geq a_{n+1}$
. If
$j\geq a_{n+1}$
. If
![]() ${s\in S_a(n)}$
, then
${s\in S_a(n)}$
, then
![]() $m_a^s$
satisfies
$m_a^s$
satisfies
![]() $(\star _1^a)$
, and if
$(\star _1^a)$
, and if
![]() $s\in S_a(n+1)\setminus S_a(n)$
, we have that
$s\in S_a(n+1)\setminus S_a(n)$
, we have that
![]() $m_a^s$
satisfies
$m_a^s$
satisfies
![]() $(\star _2^a)$
. In either case, as
$(\star _2^a)$
. In either case, as
![]() $a_n+1\geq m_a^s$
, we have that
$a_n+1\geq m_a^s$
, we have that
![]() $\psi _a(n+1,s)$
holds, and so does
$\psi _a(n+1,s)$
holds, and so does
![]() $\psi _a(n+1)$
.
$\psi _a(n+1)$
.
Step b:
Inductive hypothesis at n:
The construction is dual to that of part a. Let us start by calling
The corresponding inductive formulas for
![]() $s\in S_b(n)$
are now
$s\in S_b(n)$
are now
-
ϕ b (n, s)
 $\equiv \rho _{\mathcal {B}}(s)\geq \rho _{\mathcal {C}}(f[s])$
$\equiv \rho _{\mathcal {B}}(s)\geq \rho _{\mathcal {C}}(f[s])$
-
ψ b (n, s)
 $\equiv $
if
$\equiv $
if
 $j\geq b_n$
, then
$j\geq b_n$
, then
 $\rho _{\mathcal {B}}(s\cup \{j\})\geq \rho _{\mathcal {C}}(f[s\cup \{2n+1\}])$
.
$\rho _{\mathcal {B}}(s\cup \{j\})\geq \rho _{\mathcal {C}}(f[s\cup \{2n+1\}])$
.
We will write again
![]() $\phi _b(n)$
and
$\phi _b(n)$
and
![]() $\psi _b(n)$
as shorthands for
$\psi _b(n)$
as shorthands for
![]() $\forall s\in S_b(n)\phi _a(n,s)$
and
$\forall s\in S_b(n)\phi _a(n,s)$
and
![]() $\forall s\in S_b(n)\psi _a(n,s)$
, respectively. In the particular case of
$\forall s\in S_b(n)\psi _a(n,s)$
, respectively. In the particular case of
![]() $\phi _b$
, we have that it is the same formula as
$\phi _b$
, we have that it is the same formula as
![]() $\phi _a$
with different domain. Since
$\phi _a$
with different domain. Since
![]() $a_{n+1}$
has already been defined, the interval
$a_{n+1}$
has already been defined, the interval
![]() $[b_n,a_{n+1})$
considered in
$[b_n,a_{n+1})$
considered in
![]() $S_b(n+1)$
makes complete sense.
$S_b(n+1)$
makes complete sense.
Construction of b n+1:
Given
![]() $s\in S_b(n)$
, it follows from
$s\in S_b(n)$
, it follows from
![]() $\phi _b(n,s)$
that
$\phi _b(n,s)$
that
![]() $\rho _{\mathcal {B}}(s)\geq \rho _{\mathcal {C}}(f[s])$
, and thus, we can find
$\rho _{\mathcal {B}}(s)\geq \rho _{\mathcal {C}}(f[s])$
, and thus, we can find
![]() $m_s^b$
such that
$m_s^b$
such that
-
(⋆1 b )
 $\rho _{\mathcal {B}}(s\cup \{m\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+3\})$
for every
$\rho _{\mathcal {B}}(s\cup \{m\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+3\})$
for every
 $m\geq m_s^b$
.
$m\geq m_s^b$
.
Otherwise,
![]() $s\in S_b(n+1)\setminus S_b(n)$
, and we can write
$s\in S_b(n+1)\setminus S_b(n)$
, and we can write
![]() $s'=s\setminus \{j\}$
, where
$s'=s\setminus \{j\}$
, where
![]() $j=\max (s)\geq b_n$
and
$j=\max (s)\geq b_n$
and
![]() $s'\in S_b(n)$
. Thus,
$s'\in S_b(n)$
. Thus,
![]() $\rho _{\mathcal {B}}(s'\cup \{j\})\geq \rho _{\mathcal {C}}(f[s']\cup \{2n+1\})$
by
$\rho _{\mathcal {B}}(s'\cup \{j\})\geq \rho _{\mathcal {C}}(f[s']\cup \{2n+1\})$
by
![]() $\psi _b(n,s)$
. Since
$\psi _b(n,s)$
. Since
![]() $j\in [b_n,a_{n+1})$
, we have that
$j\in [b_n,a_{n+1})$
, we have that
![]() $f(j)=2n+1$
. Then,
$f(j)=2n+1$
. Then,
-
(* b )
 $\rho _{\mathcal {B}}(s)=\rho _{\mathcal {B}}(s'\cup \{ j\})\geq \rho _{\mathcal {C}}(f[s']\cup \{f(j)\})=\rho _{\mathcal {C}}(f[s'\cup \{j\}])=\rho _{\mathcal {C}}(f[s]).$
$\rho _{\mathcal {B}}(s)=\rho _{\mathcal {B}}(s'\cup \{ j\})\geq \rho _{\mathcal {C}}(f[s']\cup \{f(j)\})=\rho _{\mathcal {C}}(f[s'\cup \{j\}])=\rho _{\mathcal {C}}(f[s]).$
We can again find
![]() $m_s^b\in \omega $
such that
$m_s^b\in \omega $
such that
![]() $\rho _{\mathcal {B}}(s\cup \{m_s^b\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+3\})$
, and moreover,
$\rho _{\mathcal {B}}(s\cup \{m_s^b\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+3\})$
, and moreover,
-
(⋆2 b )
 $\rho _{\mathcal {B}}(s\cup \{m\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+3\})$
for every
$\rho _{\mathcal {B}}(s\cup \{m\})\geq \rho _{\mathcal {C}}(f[s]\cup \{2n+3\})$
for every
 $m\geq m_s^b$
.
$m\geq m_s^b$
.
We then define
Inductive hypothesis for n + 1:
If
![]() $s\in S_b(n)$
, then
$s\in S_b(n)$
, then
![]() $\phi _b(n+1,s)$
follows from
$\phi _b(n+1,s)$
follows from
![]() $\phi _b(n,s)$
, and otherwise,
$\phi _b(n,s)$
, and otherwise,
![]() $s\in S_b(n+1)\setminus S_b(n)$
can be written as
$s\in S_b(n+1)\setminus S_b(n)$
can be written as
![]() $s'=s\setminus \{j\}$
, where
$s'=s\setminus \{j\}$
, where
![]() $j=\max (s)$
. By
$j=\max (s)$
. By
![]() $(\ast ^b)$
, we have that
$(\ast ^b)$
, we have that
![]() $\rho _{{\mathcal {B}}}(s)\geq \rho _{{\mathcal {C}}}(f[s])$
, and then
$\rho _{{\mathcal {B}}}(s)\geq \rho _{{\mathcal {C}}}(f[s])$
, and then
![]() $\phi _b(n+1)$
holds.
$\phi _b(n+1)$
holds.
To see that
![]() $\psi _b(n+1)$
is true, let
$\psi _b(n+1)$
is true, let
![]() $s\in S_b(n+1)$
and
$s\in S_b(n+1)$
and
![]() $j\geq b_{n+1}$
. Then,
$j\geq b_{n+1}$
. Then,
![]() $b_{n+1}\geq m_s^b$
, and either by
$b_{n+1}\geq m_s^b$
, and either by
![]() $(\star _1^b)$
or
$(\star _1^b)$
or
![]() $(\star _2^b)$
, we have that
$(\star _2^b)$
, we have that
![]() $\phi _b(n+1,s)$
holds.
$\phi _b(n+1,s)$
holds.
This finishes the construction, and it remains to prove that f works.
Clearly, f is finite-to-one and nondecreasing. Given
![]() $M\in [\omega ]^\omega $
, we can find an infinite subset
$M\in [\omega ]^\omega $
, we can find an infinite subset
![]() $N\in [M]^\omega $
such that
$N\in [M]^\omega $
such that
![]() $|N\cap [k_i,k_{i+1}]|\leq 1$
for every
$|N\cap [k_i,k_{i+1}]|\leq 1$
for every
![]() $i\in \omega $
, and either
$i\in \omega $
, and either
![]() $N\cap \bigcup _{i\in \omega }[k_{2i},k_{2i+1})=\emptyset $
or
$N\cap \bigcup _{i\in \omega }[k_{2i},k_{2i+1})=\emptyset $
or
![]() $N\cap \bigcup _{i\in \omega }[k_{2i+1},k_{2i+2})=\emptyset $
. Without loss of generality, assume that
$N\cap \bigcup _{i\in \omega }[k_{2i+1},k_{2i+2})=\emptyset $
. Without loss of generality, assume that
![]() $N\subseteq \bigcup _{i\in \omega }[k_{2i},k_{2i+1})=\bigcup _{i\in \omega }[a_i,b_i)$
.
$N\subseteq \bigcup _{i\in \omega }[k_{2i},k_{2i+1})=\bigcup _{i\in \omega }[a_i,b_i)$
.
Let now
![]() $b\in {\mathcal {B}}|N$
. It follows from the choice of N that there is an
$b\in {\mathcal {B}}|N$
. It follows from the choice of N that there is an
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $b\in S_a(n)$
. By
$b\in S_a(n)$
. By
![]() $\phi _a(n,b)$
, we know that
$\phi _a(n,b)$
, we know that
![]() $0=\rho _{\mathcal {B}}(b)\geq \rho _{\mathcal {C}}(f[b])$
. Necessarily,
$0=\rho _{\mathcal {B}}(b)\geq \rho _{\mathcal {C}}(f[b])$
. Necessarily,
![]() $\rho _{\mathcal {C}}(f[b])\in \{0,-1\}$
, but in either case, we can conclude that there is
$\rho _{\mathcal {C}}(f[b])\in \{0,-1\}$
, but in either case, we can conclude that there is
![]() $c\in {\mathcal {C}}$
such that
$c\in {\mathcal {C}}$
such that
![]() $c\sqsubseteq f[b]$
. This finishes the proof.
$c\sqsubseteq f[b]$
. This finishes the proof.
The previous lemma is new, and it is the last piece of the theory of barriers that we need in order to prove that the general notion of barrier sequential compactness extending n-sequentially compact spaces depends only on the rank of the associated uniform barrier. In the case that
![]() ${\mathcal {B}}$
has rank
${\mathcal {B}}$
has rank
![]() $\omega $
, we can drop the requirement that the barrier is uniform.
$\omega $
, we can drop the requirement that the barrier is uniform.
Corollary 2.21 Let
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
be barriers on
${\mathcal {C}}$
be barriers on
![]() $\omega $
such that
$\omega $
such that
![]() $\rho ({\mathcal {C}})\leq \rho ({\mathcal {B}})=\omega $
. Then,
$\rho ({\mathcal {C}})\leq \rho ({\mathcal {B}})=\omega $
. Then,
![]() ${\mathcal {C}}\preceq {\mathcal {B}}$
.
${\mathcal {C}}\preceq {\mathcal {B}}$
.
Proof By the fact that the preorder
![]() $\preceq $
is transitive and the previous proposition, it suffices to show that
$\preceq $
is transitive and the previous proposition, it suffices to show that
![]() ${\mathcal {S}}\preceq {\mathcal {B}}$
, where
${\mathcal {S}}\preceq {\mathcal {B}}$
, where
![]() ${\mathcal {S}}$
is the Schreier barrier.
${\mathcal {S}}$
is the Schreier barrier.
Since
![]() ${\mathcal {B}}$
has rank
${\mathcal {B}}$
has rank
![]() $\omega $
, it follows from Lemma 2.9 that for every
$\omega $
, it follows from Lemma 2.9 that for every
![]() $i\in \omega $
, we can find
$i\in \omega $
, we can find
![]() $m_i$
such that
$m_i$
such that
![]() $\rho _{\mathcal {B}}(m)\geq i+1$
for every
$\rho _{\mathcal {B}}(m)\geq i+1$
for every
![]() $m\geq m_i$
. Let
$m\geq m_i$
. Let
![]() $f\in \omega ^\omega $
be given by
$f\in \omega ^\omega $
be given by
![]() $f(n)=i$
if and only if
$f(n)=i$
if and only if
![]() $n\in [m_i,m_{i+1})$
(and we define
$n\in [m_i,m_{i+1})$
(and we define
![]() $f\upharpoonright m_0$
arbitrarily). We claim that f witnesses that
$f\upharpoonright m_0$
arbitrarily). We claim that f witnesses that
![]() ${\mathcal {S}}\preceq {\mathcal {B}}$
.
${\mathcal {S}}\preceq {\mathcal {B}}$
.
Indeed, given
![]() $M\in [\omega ]^\omega $
, we can find
$M\in [\omega ]^\omega $
, we can find
![]() $N_0\in [M]^\omega $
such that
$N_0\in [M]^\omega $
such that
![]() $N_0\cap [0,m_0)=\emptyset $
and
$N_0\cap [0,m_0)=\emptyset $
and
![]() $|N_0\cap [m_i,m_{i+1})|\leq 1$
for every
$|N_0\cap [m_i,m_{i+1})|\leq 1$
for every
![]() $i\in \omega $
. Let
$i\in \omega $
. Let
![]() $n_0=\min (N_0)$
, and for every
$n_0=\min (N_0)$
, and for every
![]() $i\in \omega $
, define
$i\in \omega $
, define
![]() $n_{i+1}$
as follows: for each
$n_{i+1}$
as follows: for each
![]() $j<i+1$
, we can apply Corollary 2.10 and find
$j<i+1$
, we can apply Corollary 2.10 and find
![]() $k_j$
such that
$k_j$
such that
![]() ${\mathcal {B}}[n_j]=[\omega \setminus k_j]^r$
for some
${\mathcal {B}}[n_j]=[\omega \setminus k_j]^r$
for some
![]() $r\geq l$
, where l is the unique natural number such that
$r\geq l$
, where l is the unique natural number such that
![]() ${n_j\in [m_l,m_{l+1})}$
. Pick
${n_j\in [m_l,m_{l+1})}$
. Pick
![]() $n_{i+1}>k_j$
for every
$n_{i+1}>k_j$
for every
![]() $j<i+1$
. Thus,
$j<i+1$
. Thus,
![]() $N=\{n_i:i\in \omega \}\in [M]^\omega $
.
$N=\{n_i:i\in \omega \}\in [M]^\omega $
.
Fix
![]() $b\in ({\mathcal {B}}|N)$
and let
$b\in ({\mathcal {B}}|N)$
and let
![]() $n_i=\min (b)$
. It follows from the definitions that
$n_i=\min (b)$
. It follows from the definitions that
![]() $b\setminus \{n_i\}\in [\omega \setminus k_j]^r$
for some
$b\setminus \{n_i\}\in [\omega \setminus k_j]^r$
for some
![]() $r\geq l$
, where
$r\geq l$
, where
![]() $n_i\in [m_l,m_{l+1})$
. Then,
$n_i\in [m_l,m_{l+1})$
. Then,
![]() $|f[b]|\geq l+1$
as f is one to one on N, but
$|f[b]|\geq l+1$
as f is one to one on N, but
![]() $f(n_i)=l$
and
$f(n_i)=l$
and
![]() ${\mathcal {S}}(l)=\{s\in [\omega ]^{<\omega }:\min (s)=l\land |s|=l+1\}$
. Thus, we can conclude that
${\mathcal {S}}(l)=\{s\in [\omega ]^{<\omega }:\min (s)=l\land |s|=l+1\}$
. Thus, we can conclude that
![]() $c\sqsubseteq f[b]$
defined as the first
$c\sqsubseteq f[b]$
defined as the first
![]() $l+1$
elements of
$l+1$
elements of
![]() $f[b]$
is an element of
$f[b]$
is an element of
![]() ${\mathcal {S}}$
.
${\mathcal {S}}$
.
3 Infinite dimensional sequential compactness
We now define the notion of
![]() ${\mathcal {B}}$
-sequential compactness for barriers
${\mathcal {B}}$
-sequential compactness for barriers
![]() ${\mathcal {B}}$
and prove necessary results to formulate the natural notion of
${\mathcal {B}}$
and prove necessary results to formulate the natural notion of
![]() $\alpha $
-sequential compactness, where
$\alpha $
-sequential compactness, where
![]() $\alpha \in \omega _1$
corresponds to the rank of the barrier. All the results of this section are natural generalizations of results presented in [Reference Kubiś and Szeptycki19] for finite n.
$\alpha \in \omega _1$
corresponds to the rank of the barrier. All the results of this section are natural generalizations of results presented in [Reference Kubiś and Szeptycki19] for finite n.
Definition 3.1 Let
![]() ${\mathcal {B}}$
be a barrier on
${\mathcal {B}}$
be a barrier on
![]() $M\in [\omega ]^\omega $
, let X be a topological space,
$M\in [\omega ]^\omega $
, let X be a topological space,
![]() ${f:{\mathcal {B}}\rightarrow X}$
, and
${f:{\mathcal {B}}\rightarrow X}$
, and
![]() $x\in X$
. We say that f converges to x if for all
$x\in X$
. We say that f converges to x if for all
![]() $U\in {\mathcal {N}}(x)$
, there is
$U\in {\mathcal {N}}(x)$
, there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $f[({\mathcal {B}}|(M\setminus n))]\subseteq U$
.
$f[({\mathcal {B}}|(M\setminus n))]\subseteq U$
.
The word “converges” might give rise to misunderstanding, as f has countable domain; however, the meaning of this word will be understood by the context. The function f should be thought as a
![]() ${\mathcal {B}}$
-dimensional sequence or
${\mathcal {B}}$
-dimensional sequence or
![]() $\alpha $
-dimensional sequence for
$\alpha $
-dimensional sequence for
![]() $\alpha =\rho ({\mathcal {B}})$
rather than a classical 1-dimensional sequence indexed by the countable set
$\alpha =\rho ({\mathcal {B}})$
rather than a classical 1-dimensional sequence indexed by the countable set
![]() ${\mathcal {B}}$
.
${\mathcal {B}}$
.
Definition 3.2 Let
![]() ${\mathcal {B}}$
be a barrier on
${\mathcal {B}}$
be a barrier on
![]() $\omega $
and let X be a topological space. We say that X is
$\omega $
and let X be a topological space. We say that X is
![]() ${\mathcal {B}}$
-sequentially compact if for all
${\mathcal {B}}$
-sequentially compact if for all
![]() $f:{\mathcal {B}}\rightarrow X$
, there is
$f:{\mathcal {B}}\rightarrow X$
, there is
![]() $M\in [\omega ]^\omega $
such that
$M\in [\omega ]^\omega $
such that
![]() $f\restriction ({\mathcal {B}}|M)$
converges.
$f\restriction ({\mathcal {B}}|M)$
converges.
The natural stratification of barriers given by their ranks will give us a natural classification of
![]() ${\mathcal {B}}$
-sequentially compact spaces grouping them and associating them to a countable ordinal attending the following definition:
${\mathcal {B}}$
-sequentially compact spaces grouping them and associating them to a countable ordinal attending the following definition:
Definition 3.3 Let
![]() $\alpha <\omega _1$
. We say that X is
$\alpha <\omega _1$
. We say that X is
![]() $\alpha $
-sequentially compact if X is
$\alpha $
-sequentially compact if X is
![]() ${\mathcal {B}}$
-sequentially compact for all barriers
${\mathcal {B}}$
-sequentially compact for all barriers
![]() ${\mathcal {B}}$
of rank
${\mathcal {B}}$
of rank
![]() $\alpha $
.
$\alpha $
.
The first application of the theory developed in Section 2 and the main reason for the introduction of the order
![]() $\preceq $
is due to the next theorem:
$\preceq $
is due to the next theorem:
Theorem 3.4 If
![]() ${\mathcal {C}}\preceq {\mathcal {B}}$
and X is
${\mathcal {C}}\preceq {\mathcal {B}}$
and X is
![]() ${\mathcal {B}}$
-sequentially compact, then X is also
${\mathcal {B}}$
-sequentially compact, then X is also
![]() ${\mathcal {C}}$
-sequentially compact.
${\mathcal {C}}$
-sequentially compact.
Proof Assume X is
![]() ${\mathcal {B}}$
sequentially compact and let
${\mathcal {B}}$
sequentially compact and let
![]() $f\in \omega ^\omega $
as in the definition of
$f\in \omega ^\omega $
as in the definition of
![]() ${\mathcal {C}}\preceq {\mathcal {B}}$
. Let
${\mathcal {C}}\preceq {\mathcal {B}}$
. Let
![]() $h:{\mathcal {C}}\to X$
and define
$h:{\mathcal {C}}\to X$
and define
![]() $\hat {h}:{\mathcal {B}}\to X$
by
$\hat {h}:{\mathcal {B}}\to X$
by
![]() $\hat {h}(b)=h(c)$
for any
$\hat {h}(b)=h(c)$
for any
![]() $c\in {\mathcal {C}}$
that is
$c\in {\mathcal {C}}$
that is
![]() $\sqsubseteq $
-compatible with
$\sqsubseteq $
-compatible with
![]() $f[b]$
. Notice that since
$f[b]$
. Notice that since
![]() ${\mathcal {C}}$
is a barrier, there is at least one of such c, and then
${\mathcal {C}}$
is a barrier, there is at least one of such c, and then
![]() $\hat {h}$
is well-defined.
$\hat {h}$
is well-defined.
Since X is
![]() ${\mathcal {B}}$
-sequentially compact, there is
${\mathcal {B}}$
-sequentially compact, there is
![]() $M\in [\omega ]^\omega $
such that
$M\in [\omega ]^\omega $
such that
![]() $\hat {h}\upharpoonright ({\mathcal {B}}|M)$
converges to some
$\hat {h}\upharpoonright ({\mathcal {B}}|M)$
converges to some
![]() $x\in X$
. Take
$x\in X$
. Take
![]() $N\in [M]^\omega $
such that
$N\in [M]^\omega $
such that
given by the definition of
![]() ${\mathcal {C}}\preceq {\mathcal {B}}$
, and define
${\mathcal {C}}\preceq {\mathcal {B}}$
, and define
![]() $M_0=f[N]$
. It turns out that
$M_0=f[N]$
. It turns out that
![]() $\hat {h}\upharpoonright ({\mathcal {B}}|N)$
also converges to x. We shall prove that
$\hat {h}\upharpoonright ({\mathcal {B}}|N)$
also converges to x. We shall prove that
![]() $h\upharpoonright ({\mathcal {C}}|M_0)$
converges to the same
$h\upharpoonright ({\mathcal {C}}|M_0)$
converges to the same
![]() $x\in X$
.
$x\in X$
.
To see this, fix an open neighborhood
![]() $U\in {\mathcal {N}}(x)$
. We can find
$U\in {\mathcal {N}}(x)$
. We can find
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $\hat {h}(b)\in U$
whenever
$\hat {h}(b)\in U$
whenever
![]() $b\in {\mathcal {B}}|(N\setminus n)$
. Take
$b\in {\mathcal {B}}|(N\setminus n)$
. Take
![]() $c\in {\mathcal {C}}|(M_0\setminus f(n))$
. Thus,
$c\in {\mathcal {C}}|(M_0\setminus f(n))$
. Thus,
![]() $c=\{f(m_0),\ldots ,f(m_j)\}$
for some set
$c=\{f(m_0),\ldots ,f(m_j)\}$
for some set
![]() $a=\{m_i:i\leq j\}\subseteq N\setminus n$
. Take any infinite set
$a=\{m_i:i\leq j\}\subseteq N\setminus n$
. Take any infinite set
![]() $N'\subseteq N$
such that
$N'\subseteq N$
such that
![]() $a\sqsubseteq N'$
. We can find
$a\sqsubseteq N'$
. We can find
![]() $b\in {\mathcal {B}}|N$
such that
$b\in {\mathcal {B}}|N$
such that
![]() $b\sqsubseteq N'$
. It follows that
$b\sqsubseteq N'$
. It follows that
![]() $a\sqsubseteq b$
since otherwise,
$a\sqsubseteq b$
since otherwise,
![]() $f[b]\sqsubset f[a]=c$
would contradict that
$f[b]\sqsubset f[a]=c$
would contradict that
![]() $b\subseteq N$
. Therefore,
$b\subseteq N$
. Therefore,
![]() $h(c)=\hat {h}(b)\in U$
, as desired.
$h(c)=\hat {h}(b)\in U$
, as desired.
Corollary 3.5 Let X be a topological space and
![]() $\alpha \in \omega _1$
; the following are equivalent:
$\alpha \in \omega _1$
; the following are equivalent:
-
(1) X is
 $\alpha $
-sequentially compact,
$\alpha $
-sequentially compact, -
(2) X is
 ${\mathcal {B}}$
-sequentially compact for every uniform barrier of rank
${\mathcal {B}}$
-sequentially compact for every uniform barrier of rank
 $\alpha $
,
$\alpha $
, -
(3) X is
 ${\mathcal {B}}$
-sequentially compact for some uniform barrier
${\mathcal {B}}$
-sequentially compact for some uniform barrier
 ${\mathcal {B}}$
of rank
${\mathcal {B}}$
of rank
 $\alpha $
.
$\alpha $
.
Proof That (3) implies (1) follows directly from Proposition 2.20 and Theorem 3.4. The other implications are clear from the definitions.
From Lemma 2.20 and Theorem 3.4, we can easily get the following result.
Corollary 3.6 If X is
![]() $\alpha $
-sequentially compact and
$\alpha $
-sequentially compact and
![]() $\beta <\alpha $
, then X is
$\beta <\alpha $
, then X is
![]() $\beta $
-sequentially compact. In particular, if
$\beta $
-sequentially compact. In particular, if
![]() $\alpha $
is infinite, X is n-sequentially compact for every
$\alpha $
is infinite, X is n-sequentially compact for every
![]() $n\in \omega $
.
$n\in \omega $
.
The stronger result for barriers of rank
![]() $\omega $
given in Corollary 2.21 yields the following result:
$\omega $
given in Corollary 2.21 yields the following result:
Corollary 3.7 If X is
![]() ${\mathcal {B}}$
-sequentially compact for some barrier of rank
${\mathcal {B}}$
-sequentially compact for some barrier of rank
![]() $\omega $
(not necessarily uniform), then X is
$\omega $
(not necessarily uniform), then X is
![]() $\omega $
-sequentially compact.
$\omega $
-sequentially compact.
In general, this is not true for every countable ordinal. A trivial example is a barrier with a single node in
![]() $T({\mathcal {B}})$
of rank
$T({\mathcal {B}})$
of rank
![]() $\omega $
(let us say
$\omega $
(let us say
![]() $\{0\}$
) and such that
$\{0\}$
) and such that
![]() ${\mathcal {B}}|(\omega \setminus 1)$
is isomorphic to
${\mathcal {B}}|(\omega \setminus 1)$
is isomorphic to
![]() ${\mathcal {S}}_2$
. In this case, every infinite restriction has rank
${\mathcal {S}}_2$
. In this case, every infinite restriction has rank
![]() $\omega $
, but the barrier itself has rank
$\omega $
, but the barrier itself has rank
![]() $\omega +1$
. It is not hard to modify our constructions in Section 5 to show that, consistently, there is a
$\omega +1$
. It is not hard to modify our constructions in Section 5 to show that, consistently, there is a
![]() ${\mathcal {B}}$
sequentially compact space that is not
${\mathcal {B}}$
sequentially compact space that is not
![]() $(\omega +1)$
-sequentially compact. We do not know if the requirement that
$(\omega +1)$
-sequentially compact. We do not know if the requirement that
![]() ${\mathcal {B}}$
has an infinite restriction of rank
${\mathcal {B}}$
has an infinite restriction of rank
![]() $\alpha $
suffices in order to show that
$\alpha $
suffices in order to show that
![]() ${\mathcal {B}}$
-sequentially compact spaces are
${\mathcal {B}}$
-sequentially compact spaces are
![]() $\alpha $
-sequentially compact. We believe that the answer is “no,” but we conjecture that a weaker result is true.
$\alpha $
-sequentially compact. We believe that the answer is “no,” but we conjecture that a weaker result is true.
Conjecture 3.8 If X is
![]() ${\mathcal {B}}$
-sequentially compact, then it is
${\mathcal {B}}$
-sequentially compact, then it is
![]() $\rho _u({\mathcal {B}})$
-sequentially compact.
$\rho _u({\mathcal {B}})$
-sequentially compact.
The following easy fact is a partial answer to Conjecture 3.8.
Proposition 3.9 Let
![]() ${\mathcal {B}}$
be a barrier on
${\mathcal {B}}$
be a barrier on
![]() $\omega $
and X a
$\omega $
and X a
![]() ${\mathcal {B}}$
-sequentially compact space. If there is
${\mathcal {B}}$
-sequentially compact space. If there is
![]() $M\in [\omega ]^\omega $
such that
$M\in [\omega ]^\omega $
such that
![]() ${\mathcal {B}}|M$
is uniform and either X is not
${\mathcal {B}}|M$
is uniform and either X is not
![]() $({\mathcal {B}}|(\omega \setminus M))$
–sequentially compact or
$({\mathcal {B}}|(\omega \setminus M))$
–sequentially compact or
![]() $\omega \setminus M$
is finite, then X is
$\omega \setminus M$
is finite, then X is
![]() $\rho ({\mathcal {B}}|M)$
-sequentially compact. In particular, X is
$\rho ({\mathcal {B}}|M)$
-sequentially compact. In particular, X is
![]() $\rho _u({\mathcal {B}})$
-sequentially compact.
$\rho _u({\mathcal {B}})$
-sequentially compact.
Proof By Corollary 3.5, it is enough to prove that X is
![]() $({\mathcal {B}}|M)$
-sequentially compact. Let
$({\mathcal {B}}|M)$
-sequentially compact. Let
![]() $F:=\omega \setminus M$
. Regardless of whether F is finite or X is not
$F:=\omega \setminus M$
. Regardless of whether F is finite or X is not
![]() $({\mathcal {B}}|F)$
-sequentially compact, there exists a function
$({\mathcal {B}}|F)$
-sequentially compact, there exists a function
![]() $g:{\mathcal {B}}|F\to X$
without infinite convergence subsequences (here, convergence means convergence with respect to barriers). Now let
$g:{\mathcal {B}}|F\to X$
without infinite convergence subsequences (here, convergence means convergence with respect to barriers). Now let
![]() $f:{\mathcal {B}}|M\to X$
. We want to prove that f admits an infinite convergent subsequence
$f:{\mathcal {B}}|M\to X$
. We want to prove that f admits an infinite convergent subsequence
![]() $f\upharpoonright ({\mathcal {B}}|M')$
for some
$f\upharpoonright ({\mathcal {B}}|M')$
for some
![]() $M'\in [\omega ]^\omega $
. For this, let
$M'\in [\omega ]^\omega $
. For this, let
![]() $\hat {f}:{\mathcal {B}}\to X$
be any common extension of both f and g. As X is
$\hat {f}:{\mathcal {B}}\to X$
be any common extension of both f and g. As X is
![]() ${\mathcal {B}}$
-sequentially compact, there is
${\mathcal {B}}$
-sequentially compact, there is
![]() $N\in [\omega ]^\omega $
such that
$N\in [\omega ]^\omega $
such that
![]() $\hat {f}\restriction N$
is convergent. Now
$\hat {f}\restriction N$
is convergent. Now
![]() $N\cap F$
should be finite, since otherwise,
$N\cap F$
should be finite, since otherwise,
![]() $\hat {f}\restriction (N\cap F)$
would also be an infinite convergent subsequence for g. This way,
$\hat {f}\restriction (N\cap F)$
would also be an infinite convergent subsequence for g. This way,
![]() $N':=N\setminus F$
is infinite, and thus,
$N':=N\setminus F$
is infinite, and thus,
![]() ${\hat {f}\restriction N'=f\restriction N'}$
is an infinite convergent subsequence for f.
${\hat {f}\restriction N'=f\restriction N'}$
is an infinite convergent subsequence for f.
4 Some classes of
 $\omega _1$
-sequentially compact spaces
$\omega _1$
-sequentially compact spaces
In [Reference Kubiś and Szeptycki19], it is proved that compact metric spaces are n-sequentially compact for every
![]() $n\in \omega $
. This result extends to any
$n\in \omega $
. This result extends to any
![]() $\alpha <\omega _1$
. We will start this section by giving two classes of spaces, each containing the class of compact metric spaces, that sit at the top of the hierarchy of
$\alpha <\omega _1$
. We will start this section by giving two classes of spaces, each containing the class of compact metric spaces, that sit at the top of the hierarchy of
![]() $\alpha $
-sequentially compact spaces.
$\alpha $
-sequentially compact spaces.
Definition 4.1 We say that X is
![]() $\omega _1$
-sequentially compact if it is
$\omega _1$
-sequentially compact if it is
![]() $\alpha $
-sequentially compact for every
$\alpha $
-sequentially compact for every
![]() $\alpha <\omega _1$
.
$\alpha <\omega _1$
.
The first class of spaces that we want to show to be
![]() $\omega _1$
-sequentially compact is the class of sequentially compact spaces of character less than
$\omega _1$
-sequentially compact is the class of sequentially compact spaces of character less than
![]() ${\mathfrak {b}}$
. The fact that sequentially compact spaces of character less than
${\mathfrak {b}}$
. The fact that sequentially compact spaces of character less than
![]() ${\mathfrak {b}}$
are n-sequentially compact for every
${\mathfrak {b}}$
are n-sequentially compact for every
![]() $n\in \omega $
was proved in [Reference Kubiś and Szeptycki19].
$n\in \omega $
was proved in [Reference Kubiś and Szeptycki19].
Theorem 4.2 Suppose X is a sequentially compact space. If
![]() $\chi (X)<{\mathfrak b}$
then X is
$\chi (X)<{\mathfrak b}$
then X is
![]() $\omega _1$
-sequentially compact.
$\omega _1$
-sequentially compact.
Proof We will show by induction that X is
![]() $\alpha $
-sequentially compact for every
$\alpha $
-sequentially compact for every
![]() ${\alpha <\omega _1}$
. If
${\alpha <\omega _1}$
. If
![]() $\alpha =1$
, then X being sequentially compact is equivalent to X being 1-sequentially compact, as the only uniform barrier of rank
$\alpha =1$
, then X being sequentially compact is equivalent to X being 1-sequentially compact, as the only uniform barrier of rank
![]() $1$
is
$1$
is
![]() $[\omega ]^1$
.
$[\omega ]^1$
.
We proceed to prove the inductive step at
![]() $\beta $
, regardless of it being a successor ordinal, and hence of the form
$\beta $
, regardless of it being a successor ordinal, and hence of the form
![]() $\beta =\alpha +1$
, or a limit ordinal, which would then be the
$\beta =\alpha +1$
, or a limit ordinal, which would then be the
![]() $\operatorname {sup}\alpha _n$
, where
$\operatorname {sup}\alpha _n$
, where
![]() $\alpha _n$
form an increasing sequence. Now let
$\alpha _n$
form an increasing sequence. Now let
![]() $f:{\mathcal {B}}\to X$
be any function where
$f:{\mathcal {B}}\to X$
be any function where
![]() ${\mathcal {B}}$
is uniform of rank
${\mathcal {B}}$
is uniform of rank
![]() $\beta $
. For all
$\beta $
. For all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() ${\mathcal {B}}[n]$
is either an
${\mathcal {B}}[n]$
is either an
![]() $\alpha $
-uniform barrier on
$\alpha $
-uniform barrier on
![]() $\omega \setminus (n+1)$
or an
$\omega \setminus (n+1)$
or an
![]() $\alpha _n$
-uniform barrier if
$\alpha _n$
-uniform barrier if
![]() $\beta $
were a limit ordinal.
$\beta $
were a limit ordinal.
For all
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $f_n:{\mathcal {B}}[n]\to X$
be the function mapping
$f_n:{\mathcal {B}}[n]\to X$
be the function mapping
![]() $s\mapsto f(\{n\}\cup s)$
. By our inductive hypothesis, there is an infinite subset
$s\mapsto f(\{n\}\cup s)$
. By our inductive hypothesis, there is an infinite subset
![]() $N_0$
and a point
$N_0$
and a point
![]() $x_0\in X$
such that
$x_0\in X$
such that
![]() ${f_0\restriction ({\mathcal {B}}[0]|N_0)\rightarrow x_0}$
. Let
${f_0\restriction ({\mathcal {B}}[0]|N_0)\rightarrow x_0}$
. Let
![]() $n_0=0$
and
$n_0=0$
and
![]() $n_1=\min N_0\setminus \{0\}$
.
$n_1=\min N_0\setminus \{0\}$
.
Note that for any infinite subset A of
![]() $\omega $
and any
$\omega $
and any
![]() $n\in \omega $
,
$n\in \omega $
,
![]() ${\mathcal {B}}[n]|A$
is also uniform of rank
${\mathcal {B}}[n]|A$
is also uniform of rank
![]() $\alpha $
if
$\alpha $
if
![]() $\beta =\alpha +1$
or of rank
$\beta =\alpha +1$
or of rank
![]() $\alpha _n$
if
$\alpha _n$
if
![]() $\beta $
were a limit ordinal. Now suppose that we have defined a decreasing sequence of infinite subsets
$\beta $
were a limit ordinal. Now suppose that we have defined a decreasing sequence of infinite subsets
![]() $N_0\supseteq N_1\supseteq \dots \supseteq N_{i-1}$
and an increasing sequence
$N_0\supseteq N_1\supseteq \dots \supseteq N_{i-1}$
and an increasing sequence
![]() $n_0<n_1<\dots <n_i$
in addition to a subset
$n_0<n_1<\dots <n_i$
in addition to a subset
![]() $\{x_0,\dots ,x_{i-1}\}$
of X. Consider the function
$\{x_0,\dots ,x_{i-1}\}$
of X. Consider the function
![]() $f_{n_{i}}:({\mathcal {B}}[n_i]| N_{i-1})\rightarrow X$
. Applying our inductive hypothesis yields an infinite subset
$f_{n_{i}}:({\mathcal {B}}[n_i]| N_{i-1})\rightarrow X$
. Applying our inductive hypothesis yields an infinite subset
![]() $N_{i}\subseteq N_{i-1}$
such that
$N_{i}\subseteq N_{i-1}$
such that
![]() $f_{n_i}\restriction ({\mathcal {B}}[n_i]|N_{i})\rightarrow x_i$
, for some point
$f_{n_i}\restriction ({\mathcal {B}}[n_i]|N_{i})\rightarrow x_i$
, for some point
![]() $x_i\in X$
. We also define
$x_i\in X$
. We also define
![]() $n_{i+1}=\min (N_i\setminus \{n_0,\ldots ,n_i\})$
. Thereby, we obtain a decreasing sequence of infinite subsets
$n_{i+1}=\min (N_i\setminus \{n_0,\ldots ,n_i\})$
. Thereby, we obtain a decreasing sequence of infinite subsets
![]() $N_0\supseteq N_1\supseteq N_2\supseteq \dots $
, a subset
$N_0\supseteq N_1\supseteq N_2\supseteq \dots $
, a subset
![]() $\{x_i:i\in \omega \}$
of the space X, and a strictly increasing sequence
$\{x_i:i\in \omega \}$
of the space X, and a strictly increasing sequence
![]() $\langle n_i:i\in \omega \rangle $
such that
$\langle n_i:i\in \omega \rangle $
such that
![]() $f_{n_i}\restriction ({\mathcal {B}}[n_i]|N_i)\rightarrow x_i$
, where
$f_{n_i}\restriction ({\mathcal {B}}[n_i]|N_i)\rightarrow x_i$
, where
![]() $n_{i+1}=\min N_i\setminus \{n_0,\ldots ,n_i\}$
for all
$n_{i+1}=\min N_i\setminus \{n_0,\ldots ,n_i\}$
for all
![]() $i\in \omega $
.
$i\in \omega $
.
Since
![]() $\{x_i:i\in \omega \}\subseteq X$
and X is sequentially compact, there is a convergent subsequence,
$\{x_i:i\in \omega \}\subseteq X$
and X is sequentially compact, there is a convergent subsequence,
![]() $Y=\{x_{i_j}:j\in \omega \}$
, with limit point
$Y=\{x_{i_j}:j\in \omega \}$
, with limit point
![]() $x.$
Re-numerating the indices, we can view
$x.$
Re-numerating the indices, we can view
![]() $Y=\{x_i:i\in \omega \}$
as the convergent subsequence. Also, let
$Y=\{x_i:i\in \omega \}$
as the convergent subsequence. Also, let
![]() $N=\{n_i:i\in \omega \}$
.
$N=\{n_i:i\in \omega \}$
.
Take any open set U in X containing the point x. As
![]() $x_i\to x$
, there is an integer
$x_i\to x$
, there is an integer
![]() ${m_U\in \omega }$
such that for all
${m_U\in \omega }$
such that for all
![]() $i>m_U$
, we have that
$i>m_U$
, we have that
![]() $x_i\in U.$
Also, for all such i, there is another integer
$x_i\in U.$
Also, for all such i, there is another integer
![]() $\phi _U(n_i)$
such that
$\phi _U(n_i)$
such that
For any
![]() $j\leq m_U$
and any
$j\leq m_U$
and any
![]() $j\notin \{n_i:i\in \omega \}$
, let
$j\notin \{n_i:i\in \omega \}$
, let
![]() $\phi _U(j)=0$
. Thus, any open subset U of X containing x induces a function
$\phi _U(j)=0$
. Thus, any open subset U of X containing x induces a function
![]() $\phi _U:\omega \rightarrow \omega $
.
$\phi _U:\omega \rightarrow \omega $
.
Let
![]() $\eta (x)$
be a local neighborhood base of x of minimum size. Since
$\eta (x)$
be a local neighborhood base of x of minimum size. Since
![]() $\chi (X)<\mathfrak b$
, the set of functions
$\chi (X)<\mathfrak b$
, the set of functions
![]() $\{\phi _U:U\in \eta (x)\}$
is bounded by some increasing function
$\{\phi _U:U\in \eta (x)\}$
is bounded by some increasing function
![]() $\psi :\omega \rightarrow \omega $
; that is,
$\psi :\omega \rightarrow \omega $
; that is,
![]() $\phi _U<^*\psi $
for every
$\phi _U<^*\psi $
for every
![]() $U\in \eta (x)$
.
$U\in \eta (x)$
.
We can find an increasing subsequence
![]() $\langle m_i:i\in \omega \rangle $
of
$\langle m_i:i\in \omega \rangle $
of
![]() $\langle n_i:i\in \omega \rangle $
such that
$\langle n_i:i\in \omega \rangle $
such that
![]() $m_{i+1}>\psi (m_i)$
for every
$m_{i+1}>\psi (m_i)$
for every
![]() $i\in \omega $
. We claim that
$i\in \omega $
. We claim that
![]() $f\upharpoonright ({\mathcal {B}}|M)\to x$
, where
$f\upharpoonright ({\mathcal {B}}|M)\to x$
, where
![]() $M=\{m_i:i\in \omega \}$
.
$M=\{m_i:i\in \omega \}$
.
Fix an open set
![]() $U\in \eta (x)$
and let
$U\in \eta (x)$
and let
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $x_j\in U$
and
$x_j\in U$
and
![]() $\psi (j)>\phi _U(j)$
for every
$\psi (j)>\phi _U(j)$
for every
![]() $j\geq k$
. Let
$j\geq k$
. Let
![]() $s\in {\mathcal {B}}|(M\setminus \psi (k))$
and let us write
$s\in {\mathcal {B}}|(M\setminus \psi (k))$
and let us write
![]() $s=\{m_{k_0},\ldots ,m_{k_n}\}$
and
$s=\{m_{k_0},\ldots ,m_{k_n}\}$
and
![]() $s'=s\setminus \{m_{k_0}\}$
. Note that for every
$s'=s\setminus \{m_{k_0}\}$
. Note that for every
![]() $i>0$
, we have that
$i>0$
, we have that
as
![]() $m_{k_0}\geq \psi (k)\geq k$
. In particular,
$m_{k_0}\geq \psi (k)\geq k$
. In particular,
![]() $s'\cap \phi (m_{k_0})=\emptyset $
.
$s'\cap \phi (m_{k_0})=\emptyset $
.
Now let
![]() $j\in \omega $
such that
$j\in \omega $
such that
![]() $m_{k_0}=n_j$
. Note that if
$m_{k_0}=n_j$
. Note that if
![]() $j'>j$
, then
$j'>j$
, then
![]() $n_{j'}\in N_j$
. As any
$n_{j'}\in N_j$
. As any
![]() $m_{k_i}>m_{k_0}$
for
$m_{k_i}>m_{k_0}$
for
![]() $i>0$
and this implies that
$i>0$
and this implies that
![]() $m_{k_i}=n_{j'}$
for some
$m_{k_i}=n_{j'}$
for some
![]() $j'>j$
, we can conclude that
$j'>j$
, we can conclude that
![]() $s'\subseteq N_j$
.
$s'\subseteq N_j$
.
Combining the previous arguments, we get that
![]() $s'\subseteq N_j\setminus \phi _U(n_j)$
, and we already know that
$s'\subseteq N_j\setminus \phi _U(n_j)$
, and we already know that
![]() $s=\{n_j\}\cup s'\in {\mathcal {B}}$
, which implies that
$s=\{n_j\}\cup s'\in {\mathcal {B}}$
, which implies that
![]() $s'\in {\mathcal {B}}[n_j]$
. Therefore,
$s'\in {\mathcal {B}}[n_j]$
. Therefore,
![]() ${f(s)=f_{n_j}(s')\in U}$
by (
${f(s)=f_{n_j}(s')\in U}$
by (
![]() $\ast $
), as desired.
$\ast $
), as desired.
The second class of spaces that we shall show are
![]() $\omega _1$
-sequentially compact is the class of compact bisequential spaces. Recall that
$\omega _1$
-sequentially compact is the class of compact bisequential spaces. Recall that
![]() ${\mathcal {U}}\subseteq {\mathcal {P}}(X)$
clusters at x (often written as
${\mathcal {U}}\subseteq {\mathcal {P}}(X)$
clusters at x (often written as
![]() $x\in \overline {\mathcal {U}}$
) if
$x\in \overline {\mathcal {U}}$
) if
![]() $x\in \overline U$
for every
$x\in \overline U$
for every
![]() $U\in {\mathcal {U}}$
. Of course, if
$U\in {\mathcal {U}}$
. Of course, if
![]() ${\mathcal {U}}$
is an ultrafilter, then
${\mathcal {U}}$
is an ultrafilter, then
![]() ${\mathcal {U}}$
clusters at x is equivalent to
${\mathcal {U}}$
clusters at x is equivalent to
![]() ${\mathcal {U}}$
converging to x.
${\mathcal {U}}$
converging to x.
Definition 4.3 [Reference Michael21] Let X be a topological space and
![]() $x\in X$
. We say that X is bisequential at x if for every ultrafilter
$x\in X$
. We say that X is bisequential at x if for every ultrafilter
![]() ${\mathcal {U}}$
that converges to x, there is a countable subfamily
${\mathcal {U}}$
that converges to x, there is a countable subfamily
![]() $\{A_n: n\in \omega \}\subseteq {\mathcal {U}}$
such that for every
$\{A_n: n\in \omega \}\subseteq {\mathcal {U}}$
such that for every
![]() $W\in {\mathcal {N}}(x)$
, there is
$W\in {\mathcal {N}}(x)$
, there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $A_n\subseteq W$
. We say that X is bisequential if it bisequential at x for every
$A_n\subseteq W$
. We say that X is bisequential if it bisequential at x for every
![]() $x\in X$
.
$x\in X$
.
We say that X is (countably) bisequential if for every ultrafilter on a (countable) subset of X that clusters at
![]() $x\in X$
, there is a countable subfamily of the ultrafilter converging to x.
$x\in X$
, there is a countable subfamily of the ultrafilter converging to x.
Given a tree
![]() $T\subseteq \omega ^{<\omega }$
and
$T\subseteq \omega ^{<\omega }$
and
![]() $s\in T$
, recall that the set of successors of s in T is
$s\in T$
, recall that the set of successors of s in T is
![]() $\mathrm{succ}_T(s)=\{n\in \omega :s^\smallfrown n\in T\}$
. Given
$\mathrm{succ}_T(s)=\{n\in \omega :s^\smallfrown n\in T\}$
. Given
![]() ${\mathcal {U}}\subseteq {\mathcal {P}}(\omega )$
, we say that T is
${\mathcal {U}}\subseteq {\mathcal {P}}(\omega )$
, we say that T is
![]() ${\mathcal {U}}$
-branching if
${\mathcal {U}}$
-branching if
![]() $\mathrm{succ}_T(s)\in {\mathcal {U}}$
for every
$\mathrm{succ}_T(s)\in {\mathcal {U}}$
for every
![]() $s\in T$
. As usual, we will omit the subindex in
$s\in T$
. As usual, we will omit the subindex in
![]() $\mathrm{succ}_T$
when there is no risk of confusion. If
$\mathrm{succ}_T$
when there is no risk of confusion. If
![]() ${\mathcal {U}}$
is an ultrafilter and
${\mathcal {U}}$
is an ultrafilter and
![]() ${\mathcal {B}}$
is a barrier on
${\mathcal {B}}$
is a barrier on
![]() $\omega $
, we define an ultrafilter
$\omega $
, we define an ultrafilter
![]() ${\mathcal {U}}^{\mathcal {B}}\subseteq {\mathcal {P}}({\mathcal {B}})$
by declaring
${\mathcal {U}}^{\mathcal {B}}\subseteq {\mathcal {P}}({\mathcal {B}})$
by declaring
![]() $Y\in {\mathcal {U}}^{\mathcal {B}}$
if and only if there is an
$Y\in {\mathcal {U}}^{\mathcal {B}}$
if and only if there is an
![]() ${\mathcal {U}}$
-branching tree
${\mathcal {U}}$
-branching tree
![]() $S\subseteq T({\mathcal {B}})$
such that
$S\subseteq T({\mathcal {B}})$
such that
![]() $Y=S\cap {\mathcal {B}}$
(here, we are identifying finite subsets with finite increasing sequences on
$Y=S\cap {\mathcal {B}}$
(here, we are identifying finite subsets with finite increasing sequences on
![]() $\omega $
).
$\omega $
).
Theorem 4.4 Every compact countably bisequential space is
![]() $\omega _1$
-sequentially compact.
$\omega _1$
-sequentially compact.
Proof Let X be a compact countably bisequential space, let
![]() ${\mathcal {B}}$
be a barrier, and let
${\mathcal {B}}$
be a barrier, and let
![]() $f:{\mathcal {B}}\to X$
. Fix an ultrafilter
$f:{\mathcal {B}}\to X$
. Fix an ultrafilter
![]() ${\mathcal {U}}\subseteq {\mathcal {P}}(\omega )$
and define an ultrafilter
${\mathcal {U}}\subseteq {\mathcal {P}}(\omega )$
and define an ultrafilter
![]() ${\mathcal {V}}\subseteq {\mathcal {P}}(f[{\mathcal {B}}])\subseteq {\mathcal {P}}(X)$
by
${\mathcal {V}}\subseteq {\mathcal {P}}(f[{\mathcal {B}}])\subseteq {\mathcal {P}}(X)$
by
![]() $V\in {\mathcal {V}}$
if and only if
$V\in {\mathcal {V}}$
if and only if
![]() $f^{-1}(V)\in {\mathcal {U}}^{\mathcal {B}}$
.
$f^{-1}(V)\in {\mathcal {U}}^{\mathcal {B}}$
.
As X is compact, we can find
![]() $x\in X$
such that
$x\in X$
such that
![]() $x\in \overline {\mathcal {V}}$
, and by bisequentiality, there exists a decreasing family
$x\in \overline {\mathcal {V}}$
, and by bisequentiality, there exists a decreasing family
![]() $\{V_n:n\in \omega \}\subseteq {\mathcal {V}}$
such that for any open neighborhood
$\{V_n:n\in \omega \}\subseteq {\mathcal {V}}$
such that for any open neighborhood
![]() ${W\in {\mathcal {N}}(x)}$
, there is
${W\in {\mathcal {N}}(x)}$
, there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $V_n\subseteq W$
. Define
$V_n\subseteq W$
. Define
![]() $U_n=f^{-1}(V_n)$
for every
$U_n=f^{-1}(V_n)$
for every
![]() $n\in \omega $
and let
$n\in \omega $
and let
![]() $T_n=\{s\in T({\mathcal {B}}):\exists b\in U_n(s\subseteq b)\}$
. Then, each
$T_n=\{s\in T({\mathcal {B}}):\exists b\in U_n(s\subseteq b)\}$
. Then, each
![]() $T_n$
is a
$T_n$
is a
![]() ${\mathcal {U}}$
-branching tree.
${\mathcal {U}}$
-branching tree.
We now recursively define an infinite set
![]() $M=\{m_i:i\in \omega \}$
. Let
$M=\{m_i:i\in \omega \}$
. Let
![]() ${m_0=\min (\mathrm{succ}_{T_0}(\emptyset ))}$
. If we have already defined
${m_0=\min (\mathrm{succ}_{T_0}(\emptyset ))}$
. If we have already defined
![]() $\{m_i:i<n\}$
, define
$\{m_i:i<n\}$
, define
![]() $m_n$
such that for every
$m_n$
such that for every
![]() $s\subseteq \{m_i:i<n\}$
with
$s\subseteq \{m_i:i<n\}$
with
![]() $s\in T({\mathcal {B}})\setminus {\mathcal {B}}$
, we have that
$s\in T({\mathcal {B}})\setminus {\mathcal {B}}$
, we have that
![]() $s^\smallfrown m_n\in T_n$
. The choice of
$s^\smallfrown m_n\in T_n$
. The choice of
![]() $m_n$
is possible since every relevant s is an element of
$m_n$
is possible since every relevant s is an element of
![]() $T_0$
and the trees
$T_0$
and the trees
![]() $T_n$
are
$T_n$
are
![]() ${\mathcal {U}}$
-branching. Moreover, if
${\mathcal {U}}$
-branching. Moreover, if
![]() $s\subseteq M$
,
$s\subseteq M$
,
![]() $s\in T({\mathcal {B}})\setminus {\mathcal {B}}$
and
$s\in T({\mathcal {B}})\setminus {\mathcal {B}}$
and
![]() $\min (s)\geq m_n$
, then
$\min (s)\geq m_n$
, then
![]() $s\in T_k$
for every
$s\in T_k$
for every
![]() $k\geq n$
.
$k\geq n$
.
It remains to show that
![]() $f\upharpoonright ({\mathcal {B}}|M)$
converges to x. Fix an open set
$f\upharpoonright ({\mathcal {B}}|M)$
converges to x. Fix an open set
![]() $W\in {\mathcal {N}}(x)$
and find
$W\in {\mathcal {N}}(x)$
and find
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $V_n\subseteq W$
. Given
$V_n\subseteq W$
. Given
![]() $s\in {\mathcal {B}}|(M\setminus m_n)$
, let
$s\in {\mathcal {B}}|(M\setminus m_n)$
, let
![]() $m_k=\max (s)$
and
$m_k=\max (s)$
and
![]() ${s'=s\setminus \{m_k\}}$
. By the choice of
${s'=s\setminus \{m_k\}}$
. By the choice of
![]() $m_k$
, we have that
$m_k$
, we have that
![]() $s= {s'}^\smallfrown m_k \in T_n\cap {\mathcal {B}}=U_n$
as
$s= {s'}^\smallfrown m_k \in T_n\cap {\mathcal {B}}=U_n$
as
![]() $k\geq n$
; thus,
$k\geq n$
; thus,
![]() ${f(s)\in V_n\subseteq W}$
. Therefore,
${f(s)\in V_n\subseteq W}$
. Therefore,
![]() $f[{\mathcal {B}}|(M\setminus m_n)]\subseteq W$
.
$f[{\mathcal {B}}|(M\setminus m_n)]\subseteq W$
.
The notion of n-sequential compactness in [Reference Kubiś and Szeptycki19] was motivated by the 2-dimensional version introduced in [Reference Bojańczyk, Kopczyński and Toruńczyk3], where the main application was to show that compact metric semigroups have idempotents naturally defined as the limit of a 2-dimensional sequence. From Theorem 4.4 and the results in [Reference Bojańczyk, Kopczyński and Toruńczyk3], we can conclude the following:
Corollary 4.5 Every compact countably bisequential semigroup K has an idempotent naturally representable as the Ramsey limit of a restriction of any given
![]() $f:[\omega ]^2\to K$
.
$f:[\omega ]^2\to K$
.
We can also now conclude that some well-known classes of spaces are
![]() $\omega _1$
-sequentially compact. It is clear that if for a class of spaces
$\omega _1$
-sequentially compact. It is clear that if for a class of spaces
![]() ${\mathcal {G}}$
, hereditary under closed subsets, we have that if every separable space in
${\mathcal {G}}$
, hereditary under closed subsets, we have that if every separable space in
![]() ${\mathcal {G}}$
is
${\mathcal {G}}$
is
![]() $\omega _1$
-sequentially compact, then every space in the class is
$\omega _1$
-sequentially compact, then every space in the class is
![]() $\omega _1$
-sequentially compact.
$\omega _1$
-sequentially compact.
Roman Pol proved that separable Rosenthal compacta are bisequential [Reference Pol24]; hence, Rosenthal compacta are countably bisequential. It can also be deduced from arguments of G. Debs in [Reference Debs9] (see [Reference Todorčević26] and Lemma 6 in [Reference Todorčević25]). Therefore, we have that every Rosenthal compact space is
![]() $\omega _1$
-sequentially compact. Since every separable Eberlein compact has weight at most
$\omega _1$
-sequentially compact. Since every separable Eberlein compact has weight at most
![]() ${\mathfrak {c}}$
, and it is a result of S. Mercourakis that Eberlein compact spaces of weight at most
${\mathfrak {c}}$
, and it is a result of S. Mercourakis that Eberlein compact spaces of weight at most
![]() ${\mathfrak {c}}$
are Rosenthal compact, we also have that Eberlein compacta are
${\mathfrak {c}}$
are Rosenthal compact, we also have that Eberlein compacta are
![]() $\omega _1$
-sequentially compact. Similarly, as every separable Corson compactum is metrizable, every Corson compactum (and hence Gul’ko and Talagrand compacta) is
$\omega _1$
-sequentially compact. Similarly, as every separable Corson compactum is metrizable, every Corson compactum (and hence Gul’ko and Talagrand compacta) is
![]() $\omega _1$
-sequentially compact. For definitions of these classes and the results just mentioned, see [Reference Negrepontis23].
$\omega _1$
-sequentially compact. For definitions of these classes and the results just mentioned, see [Reference Negrepontis23].
A space X is angelic if relatively countably compact subsets of X are relatively compact, and for every relatively compact subset
![]() $A\subseteq X$
and every
$A\subseteq X$
and every
![]() $x\in \overline {A}$
, there is a sequence
$x\in \overline {A}$
, there is a sequence
![]() $\{x_n:n\in \omega \}\subseteq A$
that converges to x. It is a result of J. Bourgain, D. H. Fremlin, and M. Talagrand [Reference Bourgain, Fremlin and Talagrand5] that Rosenthal compacta are angelic spaces.
$\{x_n:n\in \omega \}\subseteq A$
that converges to x. It is a result of J. Bourgain, D. H. Fremlin, and M. Talagrand [Reference Bourgain, Fremlin and Talagrand5] that Rosenthal compacta are angelic spaces.
It was shown by Knaust in [Reference Knaust15] that Rosenthal compacta have the Ramsey property. We recall that a space X has the Ramsey property if for every function
![]() $f:[\omega ]^2\to X$
such that
$f:[\omega ]^2\to X$
such that
![]() $\lim _{i\to \infty }\lim _{j\to \infty }f(\{i,j\})=x$
, there is
$\lim _{i\to \infty }\lim _{j\to \infty }f(\{i,j\})=x$
, there is
![]() $M\in [\omega ]^\omega $
such that
$M\in [\omega ]^\omega $
such that
![]() $f\upharpoonright [M]^2\to x$
. As any 2-sequentially compact space has the Ramsey property, the fact that Rosenthal compact spaces are
$f\upharpoonright [M]^2\to x$
. As any 2-sequentially compact space has the Ramsey property, the fact that Rosenthal compact spaces are
![]() $\omega _1$
-sequentially compact is a strengthening of Knaust’s result.
$\omega _1$
-sequentially compact is a strengthening of Knaust’s result.
The lists of angelic spaces with the Ramsey property was expanded in [Reference Knaust16]; however, the question of whether every angelic space has the Ramsey property was left open. We show now that this is not the case by pointing out that the example of a sequentially compact space that is not 2-sequentially compact considered in [Reference Corral, Guzmán and López-Callejas7] is such a counterexample.
Theorem 4.6 There is an angelic space without the Ramsey property.
Proof Note that a compact space is angelic if and only if it is Fréchet. In [Reference Corral, Guzmán and López-Callejas7], an almost disjoint family
![]() ${\mathcal {A}}\subseteq [\omega \times \omega ]^\omega $
, such that
${\mathcal {A}}\subseteq [\omega \times \omega ]^\omega $
, such that
![]() ${\mathcal {F}}({\mathcal {A}})$
is Fréchet, sequentially compact, but fails to be 2-sequentially compact, is constructed. Hence,
${\mathcal {F}}({\mathcal {A}})$
is Fréchet, sequentially compact, but fails to be 2-sequentially compact, is constructed. Hence,
![]() ${\mathcal {F}}({\mathcal {A}})$
is an angelic space.
${\mathcal {F}}({\mathcal {A}})$
is an angelic space.
In order to prove that
![]() ${\mathcal {F}}({\mathcal {A}})$
is not 2-sequentially compact,
${\mathcal {F}}({\mathcal {A}})$
is not 2-sequentially compact,
![]() ${\mathcal {A}}$
was constructed so that
${\mathcal {A}}$
was constructed so that
![]() $A_n:=\{(n,m):m\in \omega \}\in {\mathcal {A}}$
for every
$A_n:=\{(n,m):m\in \omega \}\in {\mathcal {A}}$
for every
![]() $n\in \omega $
and so that
$n\in \omega $
and so that
![]() $G:[\omega ]^2\to \omega \times \omega $
, defined by
$G:[\omega ]^2\to \omega \times \omega $
, defined by
![]() $G(\{n,m\})=(n,m)$
for
$G(\{n,m\})=(n,m)$
for
![]() $n<m$
, does not converge to any point in
$n<m$
, does not converge to any point in
![]() ${\mathcal {F}}({\mathcal {A}})$
. To avoid confusion, let’s denote by
${\mathcal {F}}({\mathcal {A}})$
. To avoid confusion, let’s denote by
![]() $\ast $
the point at infinity on
$\ast $
the point at infinity on
![]() ${\mathcal {F}}({\mathcal {A}})$
. As
${\mathcal {F}}({\mathcal {A}})$
. As
![]() $\lim _{m\to \infty }(n,m)=A_n$
and any infinite subset of
$\lim _{m\to \infty }(n,m)=A_n$
and any infinite subset of
![]() ${\mathcal {A}}$
converges to
${\mathcal {A}}$
converges to
![]() $\ast $
in
$\ast $
in
![]() ${\mathcal {F}}({\mathcal {A}})$
, we get that
${\mathcal {F}}({\mathcal {A}})$
, we get that
![]() ${\lim _{n\to \infty }\lim _{m\to \infty }(n,m)=\ast} $
. Then, moreover, we have that
${\lim _{n\to \infty }\lim _{m\to \infty }(n,m)=\ast} $
. Then, moreover, we have that
![]() ${\mathcal {F}}({\mathcal {A}})$
does not have the Ramsey property.
${\mathcal {F}}({\mathcal {A}})$
does not have the Ramsey property.
5 Some examples delineating the classes of
 $\alpha $
-sequentially compact spaces.
$\alpha $
-sequentially compact spaces.
We will construct the counterexamples that show that the classes of
![]() $\alpha $
-sequentially compact spaces and related spaces do not coincide (at least consistently, in some cases), giving analogous results to those presented in [Reference Kubiś and Szeptycki19] and [Reference Corral, Guzmán and López-Callejas7].
$\alpha $
-sequentially compact spaces and related spaces do not coincide (at least consistently, in some cases), giving analogous results to those presented in [Reference Kubiś and Szeptycki19] and [Reference Corral, Guzmán and López-Callejas7].
We shall start this section by pointing out that neither of the Theorems 4.2 or 4.4 supersedes the other. Given
![]() $X\subseteq 2^\omega $
, define
$X\subseteq 2^\omega $
, define
![]() ${\mathcal {A}}_X=\{\{x\upharpoonright n:n\in \omega \}:x\in X\}$
and denote by
${\mathcal {A}}_X=\{\{x\upharpoonright n:n\in \omega \}:x\in X\}$
and denote by
![]() ${\mathcal F}({\mathcal A})$
the one-point compactifications of the
${\mathcal F}({\mathcal A})$
the one-point compactifications of the
![]() $\Psi $
-space over the almost disjoint family
$\Psi $
-space over the almost disjoint family
![]() ${\mathcal A}$
. On the one hand, if
${\mathcal A}$
. On the one hand, if
![]() $X\subseteq 2^\omega $
has size
$X\subseteq 2^\omega $
has size
![]() ${\mathfrak {c}}$
, then
${\mathfrak {c}}$
, then
![]() ${\mathcal {F}}({\mathcal {A}}_X)$
is a compact bisequential space, but its character is
${\mathcal {F}}({\mathcal {A}}_X)$
is a compact bisequential space, but its character is
![]() $|{\mathcal {A}}_X|={\mathfrak {c}}\geq {\mathfrak {b}}$
(so this space satisfies the assumptions of Theorem 4.2 but does not satisfy the assumptions of Theorem 4.4). On the other hand,
$|{\mathcal {A}}_X|={\mathfrak {c}}\geq {\mathfrak {b}}$
(so this space satisfies the assumptions of Theorem 4.2 but does not satisfy the assumptions of Theorem 4.4). On the other hand,
![]() $\omega _1$
is a first countable, sequentially compact space that is not compact (so this space satisfies the assumptions of Theorem 4.4 but does not satisfy the assumptions of Theorem 4.2). This raises the following question:
$\omega _1$
is a first countable, sequentially compact space that is not compact (so this space satisfies the assumptions of Theorem 4.4 but does not satisfy the assumptions of Theorem 4.2). This raises the following question:
Question 5.1 Is there a compact and
![]() $\omega _1$
-sequentially compact space that is not countably bisequential?
$\omega _1$
-sequentially compact space that is not countably bisequential?
We cannot expect to conclude full bisequentiality because
![]() $\omega _1+1$
is a compact and
$\omega _1+1$
is a compact and
![]() $\omega _1$
-sequentially compact space that is not bisequential. There is even an Eberlein compactum (so Fréchet) with these properties (see [Reference Cieśla6]).
$\omega _1$
-sequentially compact space that is not bisequential. There is even an Eberlein compactum (so Fréchet) with these properties (see [Reference Cieśla6]).
It is worth noting that for an almost disjoint family
![]() ${\mathcal {A}}$
, if its Franklin space
${\mathcal {A}}$
, if its Franklin space
![]() ${\mathcal {F}}({\mathcal {A}})$
is
${\mathcal {F}}({\mathcal {A}})$
is
![]() $2$
-sequentially compact, then
$2$
-sequentially compact, then
![]() ${\mathcal {A}}$
is nowhere mad. Otherwise, if
${\mathcal {A}}$
is nowhere mad. Otherwise, if
![]() ${\mathcal {A}}\upharpoonright X$
is mad with
${\mathcal {A}}\upharpoonright X$
is mad with
![]() $X\in {\mathcal {I}}({\mathcal {A}})^+$
, we can find a function
$X\in {\mathcal {I}}({\mathcal {A}})^+$
, we can find a function
![]() $f:[\omega ]^2\to X$
that does not converge in
$f:[\omega ]^2\to X$
that does not converge in
![]() ${\mathcal {F}}({\mathcal {A}})$
, as mad families are never
${\mathcal {F}}({\mathcal {A}})$
, as mad families are never
![]() $2$
-sequentially compact (see [Reference Kubiś and Szeptycki19]). Since an ad family is Fréchet if and only if it is nowhere mad, all counterexamples constructed from ad families that are at least
$2$
-sequentially compact (see [Reference Kubiś and Szeptycki19]). Since an ad family is Fréchet if and only if it is nowhere mad, all counterexamples constructed from ad families that are at least
![]() $2$
-sequentially compact in [Reference Kubiś and Szeptycki19] and [Reference Corral, Guzmán and López-Callejas7] are also Fréchet. It was also shown in [Reference Corral, Guzmán and López-Callejas7] that 2-sequentially compact spaces are
$2$
-sequentially compact in [Reference Kubiś and Szeptycki19] and [Reference Corral, Guzmán and López-Callejas7] are also Fréchet. It was also shown in [Reference Corral, Guzmán and López-Callejas7] that 2-sequentially compact spaces are
![]() $\alpha _3$
. This gives more examples of non-bisequential almost disjoint families that are Fréchet and
$\alpha _3$
. This gives more examples of non-bisequential almost disjoint families that are Fréchet and
![]() $\alpha _3$
. The existence of these kind of ad families is not known in ZFC. For more consistent examples and for the definition of
$\alpha _3$
. The existence of these kind of ad families is not known in ZFC. For more consistent examples and for the definition of
![]() $\alpha _3$
, the reader may consult [Reference Corral and Hrušák8].
$\alpha _3$
, the reader may consult [Reference Corral and Hrušák8].
It was previously shown in [Reference Kubiś and Szeptycki19] that the classes of n-sequentially compact spaces and
![]() $(n+1)$
-sequentially compact spaces do not coincide (assuming CH for
$(n+1)$
-sequentially compact spaces do not coincide (assuming CH for
![]() $n>1$
). This result was later improved by the authors in [Reference Corral, Guzmán and López-Callejas7] by showing that the same holds under weaker assumptions (e.g.,
$n>1$
). This result was later improved by the authors in [Reference Corral, Guzmán and López-Callejas7] by showing that the same holds under weaker assumptions (e.g.,
![]() ${\mathfrak {b}}={\mathfrak {c}}$
). We will show that we can also consistently differentiate between
${\mathfrak {b}}={\mathfrak {c}}$
). We will show that we can also consistently differentiate between
![]() $\alpha $
-sequentially compact and
$\alpha $
-sequentially compact and
![]() $\beta $
-sequentially compact spaces for any
$\beta $
-sequentially compact spaces for any
![]() $\alpha \not =\beta $
by stepping up the combinatorial analysis done in [Reference Corral, Guzmán and López-Callejas7] to barriers.
$\alpha \not =\beta $
by stepping up the combinatorial analysis done in [Reference Corral, Guzmán and López-Callejas7] to barriers.
We will say that
![]() $T\subseteq \omega ^{<\omega }$
is a Hechler tree if for every
$T\subseteq \omega ^{<\omega }$
is a Hechler tree if for every
![]() $s\in T$
, the set of successors of s is coinitial on
$s\in T$
, the set of successors of s is coinitial on
![]() $\omega $
(i.e., there exists
$\omega $
(i.e., there exists
![]() $k_s\in \omega $
such that
$k_s\in \omega $
such that
![]() $\mathrm{succ}_T(s)=\{i\in \omega : s^\smallfrown i\in T\}=\omega \setminus k_s$
). We can naturally associate a function
$\mathrm{succ}_T(s)=\{i\in \omega : s^\smallfrown i\in T\}=\omega \setminus k_s$
). We can naturally associate a function
![]() $h_T:T\to \omega $
to each Hechler tree T by defining
$h_T:T\to \omega $
to each Hechler tree T by defining
![]() $h_T(s)=k_s$
.
$h_T(s)=k_s$
.
For
![]() $s,t\in \omega ^{<\omega }$
, we say that
$s,t\in \omega ^{<\omega }$
, we say that
![]() $s\prec t$
if either
$s\prec t$
if either
![]() $s\sqsubset t$
or
$s\sqsubset t$
or
![]() $s=r^\smallfrown l$
,
$s=r^\smallfrown l$
,
![]() $t=r^\smallfrown m$
for some
$t=r^\smallfrown m$
for some
![]() ${r\in \omega ^{<\omega }}$
, and
${r\in \omega ^{<\omega }}$
, and
![]() $l<m$
. Here,
$l<m$
. Here,
![]() $s\sqsubset t$
means that s is a proper initial segment of t. Enumerate
$s\sqsubset t$
means that s is a proper initial segment of t. Enumerate
![]() ${\omega ^{<\omega }=\{s_i: i\in \omega \}}$
such that
${\omega ^{<\omega }=\{s_i: i\in \omega \}}$
such that
![]() $s_i\prec s_j$
implies
$s_i\prec s_j$
implies
![]() $i<j$
. We fix this enumeration for the rest of the paper.
$i<j$
. We fix this enumeration for the rest of the paper.
Definition 5.2 Let
![]() $f\in \omega ^\omega $
and let
$f\in \omega ^\omega $
and let
![]() $T\subseteq \omega ^{<\omega }$
be a Hechler tree. We define
$T\subseteq \omega ^{<\omega }$
be a Hechler tree. We define
-
•
 $T_f\subseteq \omega ^{<\omega }$
, where
$T_f\subseteq \omega ^{<\omega }$
, where
 $\emptyset \in T_f$
and
$\emptyset \in T_f$
and
 $\mathrm{succ}(s_i)=\omega \setminus f(i)$
for every
$\mathrm{succ}(s_i)=\omega \setminus f(i)$
for every
 $s_i\in T_f$
.
$s_i\in T_f$
. -
•
 $f_T\in \omega ^\omega $
, where
$f_T\in \omega ^\omega $
, where
 $f_T(n)=k$
if and only if
$f_T(n)=k$
if and only if
 $s_n\in T$
and
$s_n\in T$
and
 $\mathrm{succ}_T(s_n)=\omega \setminus k$
and
$\mathrm{succ}_T(s_n)=\omega \setminus k$
and
 $f_T(n)=0$
otherwise.
$f_T(n)=0$
otherwise.
Recall that
![]() $\textsf {FIN}\subseteq {\mathcal {P}}(\omega )$
is the ideal of finite sets of
$\textsf {FIN}\subseteq {\mathcal {P}}(\omega )$
is the ideal of finite sets of
![]() $\omega $
.
$\omega $
.
Definition 5.3 Given a barrier
![]() ${\mathcal {B}}$
, we define the ideal
${\mathcal {B}}$
, we define the ideal
![]() $\textsf {FIN}^{\mathcal {B}}$
by recursion on its rank as the set of all
$\textsf {FIN}^{\mathcal {B}}$
by recursion on its rank as the set of all
![]() $X\subseteq [\omega ]^{<\omega }$
such that
$X\subseteq [\omega ]^{<\omega }$
such that
where
![]() $\textsf {FIN}^{[\omega ]^1}=\{\{n\}:n\in \omega \}$
works as the base case.
$\textsf {FIN}^{[\omega ]^1}=\{\{n\}:n\in \omega \}$
works as the base case.
Notice that in the case of the barrier
![]() ${\mathcal {B}}=[\omega ]^n$
, the ideal
${\mathcal {B}}=[\omega ]^n$
, the ideal
![]() $\textsf {FIN}^{\mathcal {B}}$
coincides with the well-known Fubini product
$\textsf {FIN}^{\mathcal {B}}$
coincides with the well-known Fubini product
![]() $\textsf {FIN}^n$
. In general, the Fubini product
$\textsf {FIN}^n$
. In general, the Fubini product
![]() $\textsf {FIN}^\alpha $
for a countable limit ordinal
$\textsf {FIN}^\alpha $
for a countable limit ordinal
![]() $\alpha $
is not uniquely determined and depends on the choice of an increasing sequence
$\alpha $
is not uniquely determined and depends on the choice of an increasing sequence
![]() $\{\alpha _n:n\in \omega \}$
converging to
$\{\alpha _n:n\in \omega \}$
converging to
![]() $\alpha $
, the corresponding previous choices for each
$\alpha $
, the corresponding previous choices for each
![]() $\alpha _n$
, and so on. For a barrier
$\alpha _n$
, and so on. For a barrier
![]() ${\mathcal {B}}$
of rank
${\mathcal {B}}$
of rank
![]() $\alpha $
such that
$\alpha $
such that
![]() $\alpha _n=\rho ({\mathcal {B}}[n])$
forms an increasing sequence, the ideal
$\alpha _n=\rho ({\mathcal {B}}[n])$
forms an increasing sequence, the ideal
![]() $\textsf {FIN}^{\mathcal {B}}$
also coincides with a Fubini product
$\textsf {FIN}^{\mathcal {B}}$
also coincides with a Fubini product
![]() $\textsf {FIN}^\alpha $
, where the sequence
$\textsf {FIN}^\alpha $
, where the sequence
![]() $\{\alpha _n:n\in \omega \}$
is precisely the sequence converging to
$\{\alpha _n:n\in \omega \}$
is precisely the sequence converging to
![]() $\alpha $
used in the Fubini product. For more on these ideals and their presentations, the reader may consult [Reference Dobrinen10].
$\alpha $
used in the Fubini product. For more on these ideals and their presentations, the reader may consult [Reference Dobrinen10].
It follows directly from the definition that we can characterize the ideals
![]() $\textsf {FIN}^{\mathcal {B}}$
via Hechler trees.
$\textsf {FIN}^{\mathcal {B}}$
via Hechler trees.
Lemma 5.4 Let
![]() ${\mathcal {B}}$
be a barrier and
${\mathcal {B}}$
be a barrier and
![]() $X\in {\mathsf {FIN}}^{\mathcal {B}}$
. Then, there exists a Hechler tree
$X\in {\mathsf {FIN}}^{\mathcal {B}}$
. Then, there exists a Hechler tree
![]() ${H\subseteq \omega ^{<\omega }}$
such that
${H\subseteq \omega ^{<\omega }}$
such that
![]() $X\cap H\cap {\mathcal {B}}=\emptyset $
.
$X\cap H\cap {\mathcal {B}}=\emptyset $
.
Proof We prove it by induction on
![]() $\rho ({\mathcal {B}})$
. If
$\rho ({\mathcal {B}})$
. If
![]() ${\mathcal {B}}=[\omega ]^1$
and
${\mathcal {B}}=[\omega ]^1$
and
![]() $X\in \textsf {FIN}^{\mathcal {B}}=\textsf {FIN}$
, define
$X\in \textsf {FIN}^{\mathcal {B}}=\textsf {FIN}$
, define
![]() $H\subseteq \omega ^{<\omega }$
such that
$H\subseteq \omega ^{<\omega }$
such that
![]() $\emptyset \in H$
,
$\emptyset \in H$
,
![]() $\mathrm{succ}_H(\emptyset )=\omega \setminus k$
, where
$\mathrm{succ}_H(\emptyset )=\omega \setminus k$
, where
![]() $X\subseteq k$
and
$X\subseteq k$
and
![]() $\mathrm{succ}_H(s)=\omega $
for any
$\mathrm{succ}_H(s)=\omega $
for any
![]() $s\in H\setminus \{\emptyset \}$
. This H clearly works.
$s\in H\setminus \{\emptyset \}$
. This H clearly works.
Let now
![]() ${\mathcal {B}}$
be an arbitrary barrier with
${\mathcal {B}}$
be an arbitrary barrier with
![]() $\rho ({\mathcal {B}})>1$
. We may assume that
$\rho ({\mathcal {B}})>1$
. We may assume that
![]() $\{k\}\notin {\mathcal {B}}$
for every
$\{k\}\notin {\mathcal {B}}$
for every
![]() $k\in \omega $
. Fix
$k\in \omega $
. Fix
![]() $X\in \textsf {FIN}^{\mathcal {B}}$
. Thus,
$X\in \textsf {FIN}^{\mathcal {B}}$
. Thus,
![]() $\{n\in \omega :X\cap {\mathcal {B}}(n)\notin \textsf {FIN}^{{\mathcal {B}}{[n]}}\}$
is finite, and we can find
$\{n\in \omega :X\cap {\mathcal {B}}(n)\notin \textsf {FIN}^{{\mathcal {B}}{[n]}}\}$
is finite, and we can find
![]() $k\in \omega $
that contains this set. Hence, for every
$k\in \omega $
that contains this set. Hence, for every
![]() $n\in \omega \setminus k$
, there is a Hechler tree
$n\in \omega \setminus k$
, there is a Hechler tree
![]() $H_n$
with root
$H_n$
with root
![]() $\{n\}$
such that
$\{n\}$
such that
![]() $X\cap H_n\cap {\mathcal {B}}(n)=\emptyset $
. Define
$X\cap H_n\cap {\mathcal {B}}(n)=\emptyset $
. Define
![]() $H=\{\emptyset \}\cup \bigcup _{n\geq k}H_n$
. It is clear that H is a Hechler tree and
$H=\{\emptyset \}\cup \bigcup _{n\geq k}H_n$
. It is clear that H is a Hechler tree and
![]() $X\cap H\cap {\mathcal {B}}=\emptyset $
.
$X\cap H\cap {\mathcal {B}}=\emptyset $
.
Lemma 5.5 For every
![]() ${\mathcal {X}}\subseteq {\mathsf {FIN}}^{\mathcal {B}}$
with
${\mathcal {X}}\subseteq {\mathsf {FIN}}^{\mathcal {B}}$
with
![]() $|{\mathcal {X}}|<{\mathfrak {b}}$
, there is a Hechler tree
$|{\mathcal {X}}|<{\mathfrak {b}}$
, there is a Hechler tree
![]() $H\subseteq \omega ^{<\omega }$
such that for every
$H\subseteq \omega ^{<\omega }$
such that for every
![]() $X\in {\mathcal {X}}$
, there exists
$X\in {\mathcal {X}}$
, there exists
![]() $n\in \omega $
such that
$n\in \omega $
such that
Proof Let
![]() ${\mathcal {X}}\subseteq \textsf {FIN}^{\mathcal {B}}$
with
${\mathcal {X}}\subseteq \textsf {FIN}^{\mathcal {B}}$
with
![]() $|{\mathcal {X}}|<{\mathfrak {b}}$
. By Lemma 5.4, for every
$|{\mathcal {X}}|<{\mathfrak {b}}$
. By Lemma 5.4, for every
![]() $X\in {\mathcal {X}}$
, there is a Hechler tree
$X\in {\mathcal {X}}$
, there is a Hechler tree
![]() $H_X$
such that
$H_X$
such that
![]() $X\cap H_X\cap {\mathcal {B}}=\emptyset $
. Let
$X\cap H_X\cap {\mathcal {B}}=\emptyset $
. Let
![]() $f_X=f_{H_X}$
for every
$f_X=f_{H_X}$
for every
![]() $X\in {\mathcal {X}}$
. Since
$X\in {\mathcal {X}}$
. Since
![]() $|{\mathcal {X}}|<{\mathfrak {b}}$
, we can find
$|{\mathcal {X}}|<{\mathfrak {b}}$
, we can find
![]() $f\in \omega ^\omega $
such that
$f\in \omega ^\omega $
such that
![]() $f>^*f_X$
for every
$f>^*f_X$
for every
![]() $X\in {\mathcal {X}}$
. It follows from our enumeration of
$X\in {\mathcal {X}}$
. It follows from our enumeration of
![]() $\omega ^{<\omega }$
that if
$\omega ^{<\omega }$
that if
![]() $f>^*f_X$
, then there exists
$f>^*f_X$
, then there exists
![]() $n_X\in \omega $
such that if
$n_X\in \omega $
such that if
![]() $f_X(s)>f(s)$
for some
$f_X(s)>f(s)$
for some
![]() $s\neq \emptyset $
, then
$s\neq \emptyset $
, then
![]() $s\in {\mathcal {B}}(i)$
for some
$s\in {\mathcal {B}}(i)$
for some
![]() $i\leq n_X$
. Thus, letting
$i\leq n_X$
. Thus, letting
![]() $H=H_f$
, we have that
$H=H_f$
, we have that
![]() $H\setminus H_X\subseteq \bigcup _{i\leq n_X}{\mathcal {B}}(i)$
, and this implies that
$H\setminus H_X\subseteq \bigcup _{i\leq n_X}{\mathcal {B}}(i)$
, and this implies that
The following proposition appears in [Reference Kubiś and Szeptycki19] for the particular case of barriers of the form
![]() $[\omega ]^n$
. The same argument shows that this is true for every barrier, so we have the following:
$[\omega ]^n$
. The same argument shows that this is true for every barrier, so we have the following:
Proposition 5.6 Let
![]() ${\mathcal {A}}$
be an almost disjoint family on a countable set N and let
${\mathcal {A}}$
be an almost disjoint family on a countable set N and let
![]() ${\mathcal {B}}$
be a barrier. If for every function
${\mathcal {B}}$
be a barrier. If for every function
![]() $f:{\mathcal {B}}\to N$
, there is an infinite set
$f:{\mathcal {B}}\to N$
, there is an infinite set
![]() $X\in [\omega ]^\omega $
such that
$X\in [\omega ]^\omega $
such that
then
![]() ${\mathcal {F}}({\mathcal {A}})$
is
${\mathcal {F}}({\mathcal {A}})$
is
![]() ${\mathcal {B}}$
-sequentially compact.
${\mathcal {B}}$
-sequentially compact.
The following Lemma will also be helpful for proving that a space is not
![]() ${\mathcal {B}}$
-sequentially compact for some barrier
${\mathcal {B}}$
-sequentially compact for some barrier
![]() ${\mathcal {B}}$
. We say that a barrier
${\mathcal {B}}$
. We say that a barrier
![]() ${\mathcal {C}}$
is nontrivial if
${\mathcal {C}}$
is nontrivial if
![]() ${\mathcal {C}}\neq [\omega ]^1$
.
${\mathcal {C}}\neq [\omega ]^1$
.
Lemma 5.7 Let
![]() ${\mathcal {A}}$
be an almost disjoint family on a nontrivial barrier
${\mathcal {A}}$
be an almost disjoint family on a nontrivial barrier
![]() ${\mathcal {C}}$
such that
${\mathcal {C}}$
such that
![]() $|A\cap {\mathcal {C}}(n)|\leq 1$
for every
$|A\cap {\mathcal {C}}(n)|\leq 1$
for every
![]() $A\in {\mathcal {A}}$
and every
$A\in {\mathcal {A}}$
and every
![]() $n\in \omega $
. If for every
$n\in \omega $
. If for every
![]() $E\in [\omega ]^\omega $
, there exists
$E\in [\omega ]^\omega $
, there exists
![]() $A\in {\mathcal {A}}$
such that
$A\in {\mathcal {A}}$
such that
![]() $A\subseteq {\mathcal {C}}|E$
, then
$A\subseteq {\mathcal {C}}|E$
, then
![]() ${\mathcal {F}}({\mathcal {A}})$
is not
${\mathcal {F}}({\mathcal {A}})$
is not
![]() ${\mathcal {C}}$
-sequentially compact.
${\mathcal {C}}$
-sequentially compact.
Proof As
![]() ${\mathcal {C}}$
is nontrivial, we may assume without loss of generality that every element of the
${\mathcal {C}}$
is nontrivial, we may assume without loss of generality that every element of the
![]() ${\mathcal {C}}$
has size at least
${\mathcal {C}}$
has size at least
![]() $2$
; in particular,
$2$
; in particular,
![]() ${\mathcal {C}}(m)$
is infinite for every
${\mathcal {C}}(m)$
is infinite for every
![]() $m\in \omega $
.
$m\in \omega $
.
Consider
![]() $i:{\mathcal {C}}\to {\mathcal {C}}$
to be the identity map and
$i:{\mathcal {C}}\to {\mathcal {C}}$
to be the identity map and
![]() $E\in [\omega ]^\omega $
. We shall show that
$E\in [\omega ]^\omega $
. We shall show that
![]() ${i\upharpoonright ({\mathcal {C}}|E)}$
does not converge in
${i\upharpoonright ({\mathcal {C}}|E)}$
does not converge in
![]() ${\mathcal {F}}({\mathcal {A}})$
. Since
${\mathcal {F}}({\mathcal {A}})$
. Since
![]() $i[{\mathcal {C}}|E]$
is infinite, it does not converge to any isolated point in
$i[{\mathcal {C}}|E]$
is infinite, it does not converge to any isolated point in
![]() ${\mathcal {C}}$
.
${\mathcal {C}}$
.
However, if
![]() $A\in {\mathcal {A}}$
and
$A\in {\mathcal {A}}$
and
![]() $n\in \omega $
, we have that
$n\in \omega $
, we have that
![]() $|{\mathcal {C}}(m)\cap i[{\mathcal {C}}|E\setminus n]|=\omega $
for every
$|{\mathcal {C}}(m)\cap i[{\mathcal {C}}|E\setminus n]|=\omega $
for every
![]() ${m\in E\setminus n}$
, but
${m\in E\setminus n}$
, but
![]() $|A\cap {\mathcal {C}}(m)|\leq 1$
implies that
$|A\cap {\mathcal {C}}(m)|\leq 1$
implies that
![]() $i[{\mathcal {C}}|(E\setminus n)]\nsubseteq A$
, and hence, it does not converge to A. It remains to show that it does not converge to
$i[{\mathcal {C}}|(E\setminus n)]\nsubseteq A$
, and hence, it does not converge to A. It remains to show that it does not converge to
![]() $\infty $
.
$\infty $
.
Fix the neighborhood
![]() $U={\mathcal {F}}({\mathcal {A}})\setminus (\{A\}\cup A)$
of
$U={\mathcal {F}}({\mathcal {A}})\setminus (\{A\}\cup A)$
of
![]() $\infty $
for some
$\infty $
for some
![]() $A\subseteq {\mathcal {C}}|E$
and let
$A\subseteq {\mathcal {C}}|E$
and let
![]() $n\in \omega $
. As
$n\in \omega $
. As
![]() $|A\cap {\mathcal {C}}(i)|\leq 1$
for every
$|A\cap {\mathcal {C}}(i)|\leq 1$
for every
![]() $i\in \omega $
, we can find
$i\in \omega $
, we can find
![]() $c\in A\subseteq {\mathcal {C}}|E$
such that
$c\in A\subseteq {\mathcal {C}}|E$
such that
![]() $\min (c)>n$
. Thus,
$\min (c)>n$
. Thus,
![]() $c\in {\mathcal {C}}|(E\setminus n)\setminus U$
, and in consequence,
$c\in {\mathcal {C}}|(E\setminus n)\setminus U$
, and in consequence,
![]() $i[{\mathcal {C}}|(E\setminus n)]\nsubseteq U$
. Since this is true for any
$i[{\mathcal {C}}|(E\setminus n)]\nsubseteq U$
. Since this is true for any
![]() $n\in \omega $
, we get that
$n\in \omega $
, we get that
![]() $i\upharpoonright ({\mathcal {C}}|E)$
does not converge to
$i\upharpoonright ({\mathcal {C}}|E)$
does not converge to
![]() $\infty $
.
$\infty $
.
The previous lemmas allow us to show that there are spaces that are
![]() ${\mathcal {B}}$
-sequentially compact but fail to be
${\mathcal {B}}$
-sequentially compact but fail to be
![]() ${\mathcal {C}}$
-sequentially compact whenever their ideals associated satisfy a suitable relation. For this reason, it is useful to introduce the terminology of the Katětov order.
${\mathcal {C}}$
-sequentially compact whenever their ideals associated satisfy a suitable relation. For this reason, it is useful to introduce the terminology of the Katětov order.
Definition 5.8 [Reference Katětov18] Let X and Y be countable sets,
![]() ${\mathcal {I}}$
and
${\mathcal {I}}$
and
![]() ${\mathcal {J}}$
ideals on X and Y, respectively, and
${\mathcal {J}}$
ideals on X and Y, respectively, and
![]() $f:Y\rightarrow X$
.
$f:Y\rightarrow X$
.
-
(1) f is a Katětov function from
 $(Y,{\mathcal {J}})$
to
$(Y,{\mathcal {J}})$
to
 $(X,{\mathcal {I}})$
if
$(X,{\mathcal {I}})$
if
 $f^{-1}(A)\in {\mathcal {J}}$
for all
$f^{-1}(A)\in {\mathcal {J}}$
for all
 $A\in {\mathcal {I}}$
.
$A\in {\mathcal {I}}$
. -
(2)
 ${\mathcal {I}}\leq _K{\mathcal {J}}$
(
${\mathcal {I}}\leq _K{\mathcal {J}}$
(
 ${\mathcal {I}}$
is Katětov below
${\mathcal {I}}$
is Katětov below
 ${\mathcal {J}}$
) if there exists a Katětov function from
${\mathcal {J}}$
) if there exists a Katětov function from
 $(Y,{\mathcal {J}})$
to
$(Y,{\mathcal {J}})$
to
 $(X,{\mathcal {I}})$
.
$(X,{\mathcal {I}})$
.
An easy consequence of the definition is the following:
Lemma 5.9 Let
![]() ${\mathcal {I}}$
and
${\mathcal {I}}$
and
![]() ${\mathcal {J}}$
be ideals on countable sets X and Y, respectively. Then, the following are equivalent:
${\mathcal {J}}$
be ideals on countable sets X and Y, respectively. Then, the following are equivalent:
-
(1)
 ${\mathcal {I}}\not \leq _K{\mathcal {J}}$
.
${\mathcal {I}}\not \leq _K{\mathcal {J}}$
. -
(2) For every
 $f:Y\rightarrow X$
, there is
$f:Y\rightarrow X$
, there is
 $B\in {\mathcal {J}}^+$
such that
$B\in {\mathcal {J}}^+$
such that
 $f[B]\in {\mathcal {I}}$
.
$f[B]\in {\mathcal {I}}$
.
Proof To see that (1) implies (2), let
![]() $f:Y\rightarrow X$
. As
$f:Y\rightarrow X$
. As
![]() ${\mathcal {I}}\not \leq _K{\mathcal {J}}$
, f is not a Katětov function, so there is
${\mathcal {I}}\not \leq _K{\mathcal {J}}$
, f is not a Katětov function, so there is
![]() $A\in {\mathcal {I}}$
such that
$A\in {\mathcal {I}}$
such that
![]() $B:=f^{-1}(A)\in {\mathcal {J}}^+$
. Now
$B:=f^{-1}(A)\in {\mathcal {J}}^+$
. Now
![]() $f[B]\in {\mathcal {I}}$
since
$f[B]\in {\mathcal {I}}$
since
![]() $f[B]\subseteq A\in {\mathcal {I}}$
. Conversely, to see that
$f[B]\subseteq A\in {\mathcal {I}}$
. Conversely, to see that
![]() ${\mathcal {I}}\not \leq _K{\mathcal {J}}$
, let
${\mathcal {I}}\not \leq _K{\mathcal {J}}$
, let
![]() $f:Y\rightarrow X$
; we want to prove that f is not a Katětov function. So let
$f:Y\rightarrow X$
; we want to prove that f is not a Katětov function. So let
![]() $B\in {\mathcal {J}}^+$
such that
$B\in {\mathcal {J}}^+$
such that
![]() $A:=f[B]\in {\mathcal {I}}$
. Now
$A:=f[B]\in {\mathcal {I}}$
. Now
![]() $f^{-1}(A)\in {\mathcal {J}}^+$
since
$f^{-1}(A)\in {\mathcal {J}}^+$
since
![]() $B\subseteq f^{-1}(A)$
.
$B\subseteq f^{-1}(A)$
.
Besides the ideal
![]() ${\mathsf {FIN}}^{\mathcal {B}}$
, another ideal that will be useful in the constructions of counterexamples is the following:
${\mathsf {FIN}}^{\mathcal {B}}$
, another ideal that will be useful in the constructions of counterexamples is the following:
Definition 5.10 If
![]() ${\mathcal {B}}$
is a barrier on
${\mathcal {B}}$
is a barrier on
![]() $\omega $
, then
$\omega $
, then
![]() $\mathcal {G}_c({\mathcal {B}})$
is the ideal on
$\mathcal {G}_c({\mathcal {B}})$
is the ideal on
![]() ${\mathcal {B}}$
such that
${\mathcal {B}}$
such that
![]() $(\mathcal {G}_c({\mathcal {B}}))^+=\langle \{{\mathcal {B}}|X: X\in [\omega ]^\omega \}\rangle $
(i.e.,
$(\mathcal {G}_c({\mathcal {B}}))^+=\langle \{{\mathcal {B}}|X: X\in [\omega ]^\omega \}\rangle $
(i.e.,
![]() $S\subseteq {\mathcal {B}}$
is an element of
$S\subseteq {\mathcal {B}}$
is an element of
![]() $\mathcal {G}_c({\mathcal {B}})$
if and only if there is no
$\mathcal {G}_c({\mathcal {B}})$
if and only if there is no
![]() $X\in [\omega ]^\omega $
such that
$X\in [\omega ]^\omega $
such that
![]() ${\mathcal {B}}|X\subseteq S$
).
${\mathcal {B}}|X\subseteq S$
).
Note that
![]() $({\mathcal {G}}_c([\omega ]^2))^+$
is the collection of all subsets of
$({\mathcal {G}}_c([\omega ]^2))^+$
is the collection of all subsets of
![]() $[\omega ]^2$
that contain an infinite complete subgraph; that is the reason for the notation
$[\omega ]^2$
that contain an infinite complete subgraph; that is the reason for the notation
![]() ${\mathcal {G}}_c$
. Also note that the fact that
${\mathcal {G}}_c$
. Also note that the fact that
![]() $\mathcal {G}_c({\mathcal {B}})$
is closed under finite unions follows from Nash-Williams Theorem.
$\mathcal {G}_c({\mathcal {B}})$
is closed under finite unions follows from Nash-Williams Theorem.
Theorem 5.11 (
![]() ${\mathfrak {b}}={\mathfrak {c}}$
) Let
${\mathfrak {b}}={\mathfrak {c}}$
) Let
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
be two barriers such that
${\mathcal {C}}$
be two barriers such that
![]() ${\mathsf {FIN}}^{\mathcal {C}}\not \leq _K\mathcal {G}_c({\mathcal {B}})$
. Then, there is an almost disjoint family
${\mathsf {FIN}}^{\mathcal {C}}\not \leq _K\mathcal {G}_c({\mathcal {B}})$
. Then, there is an almost disjoint family
![]() ${\mathcal {A}}$
such that
${\mathcal {A}}$
such that
![]() ${\mathcal {F}}({\mathcal {A}})$
is
${\mathcal {F}}({\mathcal {A}})$
is
![]() ${\mathcal {B}}$
-sequentially compact but not
${\mathcal {B}}$
-sequentially compact but not
![]() ${\mathcal {C}}$
-sequentially compact.
${\mathcal {C}}$
-sequentially compact.
Proof Enumerate
![]() ${\mathcal {C}}^{\mathcal {B}}=\{f_\alpha :\alpha <{\mathfrak {c}}\}$
and
${\mathcal {C}}^{\mathcal {B}}=\{f_\alpha :\alpha <{\mathfrak {c}}\}$
and
![]() $[\omega ]^\omega =\{E_\alpha :\alpha <{\mathfrak {c}}\}$
. For
$[\omega ]^\omega =\{E_\alpha :\alpha <{\mathfrak {c}}\}$
. For
![]() $E\in [\omega ]^\omega $
, let
$E\in [\omega ]^\omega $
, let
![]() $E^\uparrow =T({\mathcal {C}}|E)$
. Notice that for any such E, the tree
$E^\uparrow =T({\mathcal {C}}|E)$
. Notice that for any such E, the tree
![]() $E^\uparrow $
is everywhere
$E^\uparrow $
is everywhere
![]() $\omega $
-splitting, and hence, it has infinite intersection with any Hechler tree H inside
$\omega $
-splitting, and hence, it has infinite intersection with any Hechler tree H inside
![]() ${\mathcal {C}}$
; that is,
${\mathcal {C}}$
; that is,
![]() $|E^\uparrow \cap H\cap {\mathcal {C}}|=\omega $
. Moreover, for any
$|E^\uparrow \cap H\cap {\mathcal {C}}|=\omega $
. Moreover, for any
![]() $n\in E$
, we have that
$n\in E$
, we have that
Recursively construct
![]() $\{A_\alpha :\alpha <{\mathfrak {c}}\}\subseteq [{\mathcal {C}}]^\omega $
and
$\{A_\alpha :\alpha <{\mathfrak {c}}\}\subseteq [{\mathcal {C}}]^\omega $
and
![]() $\{X_\alpha :\alpha <{\mathfrak {c}}\}\subseteq [\omega ]^\omega $
such that for all
$\{X_\alpha :\alpha <{\mathfrak {c}}\}\subseteq [\omega ]^\omega $
such that for all
![]() $\beta <\alpha <{\mathfrak {c}}$
,
$\beta <\alpha <{\mathfrak {c}}$
,
-
(1)
 $f_\alpha [{\mathcal {B}}|X_\alpha ]\in \textsf {FIN}^{\mathcal {C}}$
,
$f_\alpha [{\mathcal {B}}|X_\alpha ]\in \textsf {FIN}^{\mathcal {C}}$
, -
(2)
 $|A_\alpha \cap A_\beta |<\omega $
,
$|A_\alpha \cap A_\beta |<\omega $
, -
(3)
 $|A_\alpha \cap f_\beta [{\mathcal {B}}|X_\beta ]|<\omega $
,
$|A_\alpha \cap f_\beta [{\mathcal {B}}|X_\beta ]|<\omega $
, -
(4)
 $|A_\alpha \cap {\mathcal {C}}(n)|\leq 1$
for all
$|A_\alpha \cap {\mathcal {C}}(n)|\leq 1$
for all
 $n\in \omega $
,
$n\in \omega $
, -
(5)
 $A_\alpha \subseteq E_\alpha ^\uparrow $
.
$A_\alpha \subseteq E_\alpha ^\uparrow $
.
At step
![]() $\alpha <{\mathfrak {c}}$
, let
$\alpha <{\mathfrak {c}}$
, let
![]() $X_\alpha \in [\omega ]^\omega $
such that
$X_\alpha \in [\omega ]^\omega $
such that
![]() $f_\alpha [{\mathcal {B}}|X_\alpha ]\in {\mathsf {FIN}}^{\mathcal {C}}$
(this set exists by Lemma 5.9). Note that also every
$f_\alpha [{\mathcal {B}}|X_\alpha ]\in {\mathsf {FIN}}^{\mathcal {C}}$
(this set exists by Lemma 5.9). Note that also every
![]() $A_\beta $
with
$A_\beta $
with
![]() $\beta <\alpha $
is an element of
$\beta <\alpha $
is an element of
![]() $\textsf {FIN}^{\mathcal {C}}$
. Then, we can find a Hechler tree H as in Lemma 5.5 such that
$\textsf {FIN}^{\mathcal {C}}$
. Then, we can find a Hechler tree H as in Lemma 5.5 such that
for either
![]() $X=f_\beta [{\mathcal {B}}|X_\beta ]$
or
$X=f_\beta [{\mathcal {B}}|X_\beta ]$
or
![]() $X=A_\beta $
for some
$X=A_\beta $
for some
![]() $\beta <\alpha $
. Let
$\beta <\alpha $
. Let
![]() $A_\alpha \in [{\mathcal {C}}]^\omega $
be such that
$A_\alpha \in [{\mathcal {C}}]^\omega $
be such that
![]() $A_\alpha \subseteq H\cap {\mathcal {C}}\cap E_\alpha ^\uparrow $
and
$A_\alpha \subseteq H\cap {\mathcal {C}}\cap E_\alpha ^\uparrow $
and
![]() $|A_\alpha \cap {\mathcal {C}}(i)|\leq 1$
for every
$|A_\alpha \cap {\mathcal {C}}(i)|\leq 1$
for every
![]() $i\in \omega $
. It follows that
$i\in \omega $
. It follows that
![]() $A_\alpha \cap X\subseteq \bigcup _{i\leq n_X}{\mathcal {C}}(i)$
for some
$A_\alpha \cap X\subseteq \bigcup _{i\leq n_X}{\mathcal {C}}(i)$
for some
![]() $n_X\in \omega $
, and as
$n_X\in \omega $
, and as
![]() $|A_\alpha \cap {\mathcal {C}}(i)|\leq 1$
for every
$|A_\alpha \cap {\mathcal {C}}(i)|\leq 1$
for every
![]() $i\leq n_X$
, this intersection is finite, and (2) and (3) hold. The remaining three properties follow from the construction.
$i\leq n_X$
, this intersection is finite, and (2) and (3) hold. The remaining three properties follow from the construction.
Since
![]() $\{A\in {\mathcal {A}}:|f_\alpha [{\mathcal {B}}|X_\alpha ]\cap A|=\omega \}\subseteq \{A_\beta :\beta \leq \alpha \}$
, and this set has size less than
$\{A\in {\mathcal {A}}:|f_\alpha [{\mathcal {B}}|X_\alpha ]\cap A|=\omega \}\subseteq \{A_\beta :\beta \leq \alpha \}$
, and this set has size less than
![]() ${\mathfrak {b}}$
, by Proposition 5.6, we get that
${\mathfrak {b}}$
, by Proposition 5.6, we get that
![]() ${\mathcal {F}}({\mathcal {A}})$
is
${\mathcal {F}}({\mathcal {A}})$
is
![]() ${\mathcal {B}}$
-sequentially compact.
${\mathcal {B}}$
-sequentially compact.
However, item (5) implies that
![]() ${\mathcal {F}}({\mathcal {A}})$
is not
${\mathcal {F}}({\mathcal {A}})$
is not
![]() ${\mathcal {C}}$
-sequentially compact by Lemma 5.7, as
${\mathcal {C}}$
-sequentially compact by Lemma 5.7, as
![]() $\mathcal C$
has rank greater than 1.
$\mathcal C$
has rank greater than 1.
The natural question now is when do the barriers
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
satisfy that
${\mathcal {C}}$
satisfy that
![]() ${\mathsf {FIN}}^{\mathcal {C}}\not \leq _K\mathcal {G}_c({\mathcal {B}})$
? We will see below that this only depends on the rank of the barriers, assuming that at least the one with larger rank is uniform. See Theorem 5.12 and Corollary 5.14 below.
${\mathsf {FIN}}^{\mathcal {C}}\not \leq _K\mathcal {G}_c({\mathcal {B}})$
? We will see below that this only depends on the rank of the barriers, assuming that at least the one with larger rank is uniform. See Theorem 5.12 and Corollary 5.14 below.
The relevance of the Katětov order in the study of subclasses of sequentially compact spaces is also demonstrated in the work of R. Filipów, K. Kowitz, and A. Kwela [Reference Filipów, Kowitz and Kwela13], where the authors study many subclasses of sequentially compact spaces, prove some inclusions among them, and find counterexamples by using the Katětov order relationship between some ideals naturally associated to these classes.
Recall that for
![]() ${\mathcal {B}}$
being a barrier,
${\mathcal {B}}$
being a barrier,
![]() ${\mathcal {B}}[s]$
is a barrier on
${\mathcal {B}}[s]$
is a barrier on
![]() $\omega \setminus (\max (s)+1)$
. For the ease of notation, we will do some abuse of notation: for a function
$\omega \setminus (\max (s)+1)$
. For the ease of notation, we will do some abuse of notation: for a function
![]() $g:{\mathcal {B}}(s)\to {\mathcal {C}}(t)$
, we can naturally associate a function
$g:{\mathcal {B}}(s)\to {\mathcal {C}}(t)$
, we can naturally associate a function
![]() $g':{\mathcal {B}}[s]\to {\mathcal {C}}[t]$
. We use g for both functions. Also, for a Hechler tree H, we will denote by
$g':{\mathcal {B}}[s]\to {\mathcal {C}}[t]$
. We use g for both functions. Also, for a Hechler tree H, we will denote by
![]() $H[n]$
its copy above
$H[n]$
its copy above
![]() $\{n\}$
– that is, a tree T with root
$\{n\}$
– that is, a tree T with root
![]() $\{n\}$
and such that
$\{n\}$
and such that
![]() $\mathrm{succ}_T(s)=\mathrm{succ}_H(s\setminus \{n\})$
. In particular,
$\mathrm{succ}_T(s)=\mathrm{succ}_H(s\setminus \{n\})$
. In particular,
![]() $\omega ^{<\omega }[n]=\{s\in \omega ^{<\omega }:n=\min (s)\}$
.
$\omega ^{<\omega }[n]=\{s\in \omega ^{<\omega }:n=\min (s)\}$
.
Theorem 5.12 Let
![]() ${\mathcal {B}},{\mathcal {C}}$
be barriers with
${\mathcal {B}},{\mathcal {C}}$
be barriers with
![]() ${\mathcal {C}}$
uniform and
${\mathcal {C}}$
uniform and
![]() $\rho ({\mathcal {B}})<\rho ({\mathcal {C}})$
. Then,
$\rho ({\mathcal {B}})<\rho ({\mathcal {C}})$
. Then,
![]() ${\mathsf {FIN}}^{\mathcal {C}}\not \leq _K\mathcal {G}_c({\mathcal {B}})$
.
${\mathsf {FIN}}^{\mathcal {C}}\not \leq _K\mathcal {G}_c({\mathcal {B}})$
.
Proof By Lemma 5.9, it is enough to prove that for every
![]() $f:{\mathcal {B}}\to {\mathcal {C}}$
, there is
$f:{\mathcal {B}}\to {\mathcal {C}}$
, there is
![]() $X\in [\omega ]^\omega $
such that
$X\in [\omega ]^\omega $
such that
![]() $f[{\mathcal {B}}|X]\in {\mathsf {FIN}}^{\mathcal {C}}$
. The proof is by induction on
$f[{\mathcal {B}}|X]\in {\mathsf {FIN}}^{\mathcal {C}}$
. The proof is by induction on
![]() $\rho ({\mathcal {C}})$
. If
$\rho ({\mathcal {C}})$
. If
![]() $\rho ({\mathcal {C}})=1$
, there is nothing to do, so we can assume that
$\rho ({\mathcal {C}})=1$
, there is nothing to do, so we can assume that
![]() $\rho ({\mathcal {C}})>1$
, and the result is true for
$\rho ({\mathcal {C}})>1$
, and the result is true for
![]() ${\mathcal {C}}'$
whenever
${\mathcal {C}}'$
whenever
![]() $\rho ({\mathcal {C}}')<\rho ({\mathcal {C}})$
. We now prove it by induction on
$\rho ({\mathcal {C}}')<\rho ({\mathcal {C}})$
. We now prove it by induction on
![]() $\rho ({\mathcal {B}})$
. If
$\rho ({\mathcal {B}})$
. If
![]() $\rho ({\mathcal {B}})=1$
, we can find an infinite set
$\rho ({\mathcal {B}})=1$
, we can find an infinite set
![]() $X\in [\omega ]^\omega $
such that either
$X\in [\omega ]^\omega $
such that either
![]() $|f[{\mathcal {B}}|X]\cap {\mathcal {C}}(i)|\leq 1$
for every
$|f[{\mathcal {B}}|X]\cap {\mathcal {C}}(i)|\leq 1$
for every
![]() $i\in \omega $
or
$i\in \omega $
or
![]() $f[{\mathcal {B}}|X]\subseteq {\mathcal {C}}(n)$
for some
$f[{\mathcal {B}}|X]\subseteq {\mathcal {C}}(n)$
for some
![]() $n\in \omega $
. Hence, assume that for any barriers
$n\in \omega $
. Hence, assume that for any barriers
![]() ${\mathcal {B}}'$
and
${\mathcal {B}}'$
and
![]() ${\mathcal {C}}'$
with
${\mathcal {C}}'$
with
![]() $\rho ({\mathcal {B}}')<\rho ({\mathcal {B}})$
,
$\rho ({\mathcal {B}}')<\rho ({\mathcal {B}})$
,
![]() $\rho ({\mathcal {C}}')\leq \rho ({\mathcal {C}})$
, and
$\rho ({\mathcal {C}}')\leq \rho ({\mathcal {C}})$
, and
![]() $\rho ({\mathcal {B}}')<\rho ({\mathcal {C}}')$
, the result holds. We can also think of
$\rho ({\mathcal {B}}')<\rho ({\mathcal {C}}')$
, the result holds. We can also think of
![]() $\{\emptyset \}$
as a barrier of rank 0. In this case, the result is trivial, but it is worth mentioning since
$\{\emptyset \}$
as a barrier of rank 0. In this case, the result is trivial, but it is worth mentioning since
![]() ${\mathcal {B}}[s]$
is a barrier of rank 0 whenever
${\mathcal {B}}[s]$
is a barrier of rank 0 whenever
![]() $s\in {\mathcal {B}}$
. We will also consider these kind of barriers as part of our inductive hypothesis. We can also assume, by possibly passing to a cofinite set, that
$s\in {\mathcal {B}}$
. We will also consider these kind of barriers as part of our inductive hypothesis. We can also assume, by possibly passing to a cofinite set, that
![]() $\rho ({\mathcal {C}}(n))\geq \rho ({\mathcal {B}})$
for every
$\rho ({\mathcal {C}}(n))\geq \rho ({\mathcal {B}})$
for every
![]() $n\in \omega $
.
$n\in \omega $
.
Define a function
![]() $\pi _n:{\mathcal {B}}\to 2$
for every
$\pi _n:{\mathcal {B}}\to 2$
for every
![]() $n\in \omega $
given by
$n\in \omega $
given by
![]() $\pi _n(s)=0$
if and only if
$\pi _n(s)=0$
if and only if
![]() $f(s)\in \bigcup _{i\leq n}{\mathcal {C}}(i)$
. By Nash-Williams, we can find an infinite set
$f(s)\in \bigcup _{i\leq n}{\mathcal {C}}(i)$
. By Nash-Williams, we can find an infinite set
![]() $Z_n\in [\omega ]^\omega $
such that
$Z_n\in [\omega ]^\omega $
such that
![]() $\pi _n\upharpoonright ({\mathcal {B}}|Z_n)$
is constant. If
$\pi _n\upharpoonright ({\mathcal {B}}|Z_n)$
is constant. If
![]() $\pi _n\upharpoonright ({\mathcal {B}}|Z_n)$
is constant with value i, we will say that
$\pi _n\upharpoonright ({\mathcal {B}}|Z_n)$
is constant with value i, we will say that
![]() $Z_n$
is a monochromatic set with color i. If for some
$Z_n$
is a monochromatic set with color i. If for some
![]() $n\in \omega $
we can find a monochromatic set
$n\in \omega $
we can find a monochromatic set
![]() $Z_n$
with color
$Z_n$
with color
![]() $0$
, then f maps
$0$
, then f maps
![]() ${\mathcal {B}}|Z_n$
into the union of the first
${\mathcal {B}}|Z_n$
into the union of the first
![]() $n+1$
-cones of
$n+1$
-cones of
![]() ${\mathcal {C}}$
, which is an element of
${\mathcal {C}}$
, which is an element of
![]() $\textsf {FIN}({\mathcal {C}})$
. Hence, we can assume that there is no monochromatic set with color
$\textsf {FIN}({\mathcal {C}})$
. Hence, we can assume that there is no monochromatic set with color
![]() $0$
for every
$0$
for every
![]() $n\in \omega $
.
$n\in \omega $
.
Let us recursively define
![]() $\{X_n:n\in \omega \}$
,
$\{X_n:n\in \omega \}$
,
![]() $\{m_i:i\in \omega \}$
,
$\{m_i:i\in \omega \}$
,
![]() $\{H_n:n\in \omega \}$
and
$\{H_n:n\in \omega \}$
and
![]() $\{g(s,n):s\subseteq \{m_i:i<n\}\land n\in \omega \}$
such that
$\{g(s,n):s\subseteq \{m_i:i<n\}\land n\in \omega \}$
such that
-
(1)
 $m_i=\min (X_i)$
,
$m_i=\min (X_i)$
, -
(2)
 $\pi _n\upharpoonright ({\mathcal {B}}|X_n)$
is constant with value 1,
$\pi _n\upharpoonright ({\mathcal {B}}|X_n)$
is constant with value 1, -
(3)
 $X_{n+1}\subseteq X_n\subset \omega $
,
$X_{n+1}\subseteq X_n\subset \omega $
, -
(4)
 $g(s,n):{\mathcal {B}}[s]\to {\mathcal {C}}[n]$
is given by
$g(s,n):{\mathcal {B}}[s]\to {\mathcal {C}}[n]$
is given by
 $g(s,n)(t)=f(t)\setminus \{n\}$
if and only if
$g(s,n)(t)=f(t)\setminus \{n\}$
if and only if
 $f(t)\in {\mathcal {C}}(n)$
, and otherwise, let
$f(t)\in {\mathcal {C}}(n)$
, and otherwise, let
 $g(s,n)(t)\in {\mathcal {C}}[n]$
be arbitrary.
$g(s,n)(t)\in {\mathcal {C}}[n]$
be arbitrary. -
(5)
 $H_n\subseteq \omega ^{<\omega }[n]$
is a Hechler tree.
$H_n\subseteq \omega ^{<\omega }[n]$
is a Hechler tree. -
(6)
 $g(s,n)[{\mathcal {B}}[s]|X_n]\cap H_n=\emptyset $
for every
$g(s,n)[{\mathcal {B}}[s]|X_n]\cap H_n=\emptyset $
for every
 $s\subseteq \{m_i:i< n\}$
with
$s\subseteq \{m_i:i< n\}$
with
 $s\neq \emptyset $
.
$s\neq \emptyset $
.
Assume
![]() $X_i, m_i, H_i$
, and
$X_i, m_i, H_i$
, and
![]() $g(s,i)$
have been defined for
$g(s,i)$
have been defined for
![]() $i\leq n$
and s as above. Since
$i\leq n$
and s as above. Since
![]() $g(s,n+1)$
is defined from
$g(s,n+1)$
is defined from
![]() $\{m_i:i\leq n\}$
and
$\{m_i:i\leq n\}$
and
![]() $m_{n+1}$
is defined from
$m_{n+1}$
is defined from
![]() $X_{n+1}$
, we only need to define
$X_{n+1}$
, we only need to define
![]() $X_{n+1}$
and
$X_{n+1}$
and
![]() $H_{n+1}$
. Note that if in point (6) we have that
$H_{n+1}$
. Note that if in point (6) we have that
![]() $s\notin T({\mathcal {B}})$
, then
$s\notin T({\mathcal {B}})$
, then
![]() ${\mathcal {B}}(s)=\emptyset $
and then any choice of
${\mathcal {B}}(s)=\emptyset $
and then any choice of
![]() $X_n$
and
$X_n$
and
![]() $H_n$
work, so we will assume in the rest of the proof that
$H_n$
work, so we will assume in the rest of the proof that
![]() $s\in T({\mathcal {B}})$
.
$s\in T({\mathcal {B}})$
.
We can find a
![]() $\pi _{n+1}$
monochromatic set (with color 1)
$\pi _{n+1}$
monochromatic set (with color 1)
![]() $X'\subseteq X_n$
. Enumerate as
$X'\subseteq X_n$
. Enumerate as
![]() ${\{s_i:i\leq k\}}$
for some
${\{s_i:i\leq k\}}$
for some
![]() $k\in \omega $
the set
$k\in \omega $
the set
![]() $\{s\subseteq \{m_i:i\leq n\}:s\in T({\mathcal {B}})\setminus \{\emptyset \}\}$
. We can recursively define
$\{s\subseteq \{m_i:i\leq n\}:s\in T({\mathcal {B}})\setminus \{\emptyset \}\}$
. We can recursively define
![]() $X_{n+1}^0\subseteq X'$
,
$X_{n+1}^0\subseteq X'$
,
![]() $X_{n+1}^{i+1}\subseteq X_{n+1}^i$
for
$X_{n+1}^{i+1}\subseteq X_{n+1}^i$
for
![]() $i<k$
and
$i<k$
and
![]() $H_{n+1}^i\subseteq {\mathcal {C}}[n+1]$
for
$H_{n+1}^i\subseteq {\mathcal {C}}[n+1]$
for
![]() $i\leq k$
such that
$i\leq k$
such that
-
(*)
 $g(s,n+1)[{\mathcal {B}}[s]|X_{n+1}^i]\cap H_{n+1}^i=\emptyset .$
$g(s,n+1)[{\mathcal {B}}[s]|X_{n+1}^i]\cap H_{n+1}^i=\emptyset .$
To see that the choices of
![]() $X_{n+1}^i$
and
$X_{n+1}^i$
and
![]() $H_{n+1}^i$
are possible, note that
$H_{n+1}^i$
are possible, note that
![]() $g(s,n+1):{\mathcal {B}}[s]\to {\mathcal {C}}[n+1]$
and
$g(s,n+1):{\mathcal {B}}[s]\to {\mathcal {C}}[n+1]$
and
![]() $\rho ({\mathcal {B}}[s])<\rho ({\mathcal {B}})\leq \rho ({\mathcal {C}}[n+1])$
. Then, we can apply the inductive hypothesis. Without loss of generality, we can assume that
$\rho ({\mathcal {B}}[s])<\rho ({\mathcal {B}})\leq \rho ({\mathcal {C}}[n+1])$
. Then, we can apply the inductive hypothesis. Without loss of generality, we can assume that
![]() $\min (X_{n+1}^i)>m_n$
for every
$\min (X_{n+1}^i)>m_n$
for every
![]() $i\leq k$
. Also, since each
$i\leq k$
. Also, since each
![]() $H_{n+1}^i$
is a Hechler tree for every
$H_{n+1}^i$
is a Hechler tree for every
![]() $i\leq k$
, we can define
$i\leq k$
, we can define
![]() $H_{n+1}=\bigcap _{i\leq k}H_{n+1}^i$
, which is a Hechler tree in
$H_{n+1}=\bigcap _{i\leq k}H_{n+1}^i$
, which is a Hechler tree in
![]() ${\mathcal {C}}[n+1]$
. Define
${\mathcal {C}}[n+1]$
. Define
![]() $X_{n+1}=X_{n+1}^k$
. This finishes the construction.
$X_{n+1}=X_{n+1}^k$
. This finishes the construction.
Let
![]() $X=\{x_i:i\in \omega \}$
and
$X=\{x_i:i\in \omega \}$
and
![]() $H=\{\emptyset \}\cup \bigcup _{n\in \omega }n^\smallfrown H_n$
. We shall show that
$H=\{\emptyset \}\cup \bigcup _{n\in \omega }n^\smallfrown H_n$
. We shall show that
![]() ${f[{\mathcal {B}}|X]\cap H=\emptyset }$
. Fix
${f[{\mathcal {B}}|X]\cap H=\emptyset }$
. Fix
![]() $s\in {\mathcal {B}}|X$
; then,
$s\in {\mathcal {B}}|X$
; then,
![]() $s=(x_{i_0},\ldots ,x_{i_k})$
for some
$s=(x_{i_0},\ldots ,x_{i_k})$
for some
![]() $k\in \omega $
and some sequence
$k\in \omega $
and some sequence
![]() $i_0<\cdots <i_k$
. As
$i_0<\cdots <i_k$
. As
![]() $\{x_{i_0},\ldots ,x_{i_k}\}\subseteq X_{i_0}$
and
$\{x_{i_0},\ldots ,x_{i_k}\}\subseteq X_{i_0}$
and
![]() $X_{i_0}$
is
$X_{i_0}$
is
![]() $\pi _{i_0}$
monochromatic with color 1, we have that
$\pi _{i_0}$
monochromatic with color 1, we have that
![]() $f(s)\in C(n)$
for some
$f(s)\in C(n)$
for some
![]() $n>i_0$
. Let
$n>i_0$
. Let
![]() $s'=\{x_i\in s:i< n\}$
and notice that
$s'=\{x_i\in s:i< n\}$
and notice that
![]() $s\setminus s'\subseteq X_n$
and
$s\setminus s'\subseteq X_n$
and
![]() $s'\neq \emptyset $
. Hence,
$s'\neq \emptyset $
. Hence,
![]() $g(s',n)$
was considered at step n in (6), and
$g(s',n)$
was considered at step n in (6), and
![]() $s'$
was indexed as
$s'$
was indexed as
![]() $s_i$
for some i. Since we have that
$s_i$
for some i. Since we have that
![]() $H\cap \omega ^{<\omega }[n]\subseteq H_n^i$
,
$H\cap \omega ^{<\omega }[n]\subseteq H_n^i$
,
![]() $s\setminus s'\in {\mathcal {B}}[s']|X_n$
, and
$s\setminus s'\in {\mathcal {B}}[s']|X_n$
, and
![]() $X_n\subseteq X_n^i$
, we can conclude, by
$X_n\subseteq X_n^i$
, we can conclude, by
![]() $(\ast )$
, that
$(\ast )$
, that
![]() $g(s',n)(s)=f(s)\setminus \{n\}\in {\mathcal {C}}[n]\setminus H_n$
, so
$g(s',n)(s)=f(s)\setminus \{n\}\in {\mathcal {C}}[n]\setminus H_n$
, so
![]() $f(s)=n^\smallfrown g(s',n)\notin H$
. Therefore,
$f(s)=n^\smallfrown g(s',n)\notin H$
. Therefore,
![]() $f[{\mathcal {B}}|X]\cap H=\emptyset $
, so
$f[{\mathcal {B}}|X]\cap H=\emptyset $
, so
![]() $f[{\mathcal {B}}|X]\in {\mathsf {FIN}}^{\mathcal {C}}$
.
$f[{\mathcal {B}}|X]\in {\mathsf {FIN}}^{\mathcal {C}}$
.
It is worth noting that the previous result gives us that for two barriers
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
, the classes of
${\mathcal {C}}$
, the classes of
![]() ${\mathcal {B}}$
-sequentially compact spaces and
${\mathcal {B}}$
-sequentially compact spaces and
![]() ${\mathcal {C}}$
-sequentially compact spaces only depend on the ranks of
${\mathcal {C}}$
-sequentially compact spaces only depend on the ranks of
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
whenever the largest is uniform. If
${\mathcal {C}}$
whenever the largest is uniform. If
![]() $\rho ({\mathcal {B}})<\rho ({\mathcal {C}})$
and
$\rho ({\mathcal {B}})<\rho ({\mathcal {C}})$
and
![]() ${\mathcal {C}}$
is uniform, every
${\mathcal {C}}$
is uniform, every
![]() ${\mathcal {C}}$
-sequentially compact space is
${\mathcal {C}}$
-sequentially compact space is
![]() ${\mathcal {B}}$
-sequentially compact by Corollaries 3.5 and 3.6. However, there are (at least consistently) examples of
${\mathcal {B}}$
-sequentially compact by Corollaries 3.5 and 3.6. However, there are (at least consistently) examples of
![]() ${\mathcal {B}}$
-sequentially compact spaces that are not
${\mathcal {B}}$
-sequentially compact spaces that are not
![]() ${\mathcal {C}}$
-sequentially compact by Theorem 5.12. If otherwise,
${\mathcal {C}}$
-sequentially compact by Theorem 5.12. If otherwise,
![]() $\rho ({\mathcal {B}})=\rho ({\mathcal {C}})$
and both of them are uniform, then the classes of
$\rho ({\mathcal {B}})=\rho ({\mathcal {C}})$
and both of them are uniform, then the classes of
![]() ${\mathcal {B}}$
-sequentially compact and
${\mathcal {B}}$
-sequentially compact and
![]() ${\mathcal {C}}$
-sequentially compact spaces coincide by Corollary 3.5.
${\mathcal {C}}$
-sequentially compact spaces coincide by Corollary 3.5.
A more subtle analysis can be done by considering
![]() $\rho _u({\mathcal {B}})$
instead of
$\rho _u({\mathcal {B}})$
instead of
![]() $\rho ({\mathcal {B}})$
, but what we have done suffices to show that (consistently) the classes of
$\rho ({\mathcal {B}})$
, but what we have done suffices to show that (consistently) the classes of
![]() $\alpha $
-sequentially compact and
$\alpha $
-sequentially compact and
![]() $\beta $
-sequentially compact spaces do not coincide if
$\beta $
-sequentially compact spaces do not coincide if
![]() $\alpha \neq \beta $
.
$\alpha \neq \beta $
.
Corollary 5.13 (
![]() ${\mathfrak {b}}={\mathfrak {c}}$
) If
${\mathfrak {b}}={\mathfrak {c}}$
) If
![]() $\{\alpha _n:n\in \omega \}\subseteq \alpha $
, there exists a space that is
$\{\alpha _n:n\in \omega \}\subseteq \alpha $
, there exists a space that is
![]() $\alpha _n$
-sequentially compact for all
$\alpha _n$
-sequentially compact for all
![]() $n\in \omega $
but fails to be
$n\in \omega $
but fails to be
![]() $\alpha $
-sequentially compact. In particular, for every
$\alpha $
-sequentially compact. In particular, for every
![]() ${\alpha <\beta <\omega _1}$
, there exists an
${\alpha <\beta <\omega _1}$
, there exists an
![]() $\alpha $
-sequentially compact space that is not
$\alpha $
-sequentially compact space that is not
![]() $\beta $
-sequentially compact.
$\beta $
-sequentially compact.
Proof Fix a uniform barrier
![]() ${\mathcal {B}}_n$
of rank
${\mathcal {B}}_n$
of rank
![]() $\alpha _n$
for every
$\alpha _n$
for every
![]() $n\in \omega $
and a barrier
$n\in \omega $
and a barrier
![]() ${\mathcal {C}}$
of rank
${\mathcal {C}}$
of rank
![]() $\alpha $
. Repeat the proof of theorem 5.11 by enumerating
$\alpha $
. Repeat the proof of theorem 5.11 by enumerating
The hypothesis of Theorem 5.11 for every barrier
![]() ${\mathcal {B}}_n$
holds by Theorem 5.12. Finally, by Corollary 3.5, we get the result.
${\mathcal {B}}_n$
holds by Theorem 5.12. Finally, by Corollary 3.5, we get the result.
If
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
are barriers with the same rank and
${\mathcal {C}}$
are barriers with the same rank and
![]() ${\mathcal {B}}$
is uniform, then
${\mathcal {B}}$
is uniform, then
![]() ${\mathsf {FIN}}^{\mathcal {C}}\leq _K{\mathcal {G}}_c({\mathcal {B}})$
. To see this, note that otherwise, by Theorem 5.11, there is a space X that is
${\mathsf {FIN}}^{\mathcal {C}}\leq _K{\mathcal {G}}_c({\mathcal {B}})$
. To see this, note that otherwise, by Theorem 5.11, there is a space X that is
![]() ${\mathcal {B}}$
-seq compact but not
${\mathcal {B}}$
-seq compact but not
![]() ${\mathcal {C}}$
-seq compact under
${\mathcal {C}}$
-seq compact under
![]() ${\mathfrak {b}}={\mathfrak {c}}$
, but this is a contradiction to Corollary 3.5 since the Katětov order is absolute among Borel ideals due to Shoenfield’s absoluteness Theorem (see [Reference Hrušák17]). We then get the following corollary:
${\mathfrak {b}}={\mathfrak {c}}$
, but this is a contradiction to Corollary 3.5 since the Katětov order is absolute among Borel ideals due to Shoenfield’s absoluteness Theorem (see [Reference Hrušák17]). We then get the following corollary:
Corollary 5.14 Let
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {C}}$
be uniform barriers such that
${\mathcal {C}}$
be uniform barriers such that
![]() $\rho ({\mathcal {B}})\leq \rho ({\mathcal {C}})$
. Then, the following are equivalent:
$\rho ({\mathcal {B}})\leq \rho ({\mathcal {C}})$
. Then, the following are equivalent:
-
(1)
 ${\mathsf {FIN}}^{\mathcal {C}}\not \leq _K{\mathcal {G}}_c({\mathcal {B}})$
.
${\mathsf {FIN}}^{\mathcal {C}}\not \leq _K{\mathcal {G}}_c({\mathcal {B}})$
. -
(2)
 $\rho ({\mathcal {B}})<\rho ({\mathcal {C}})$
.
$\rho ({\mathcal {B}})<\rho ({\mathcal {C}})$
.
It is worth pointing out that for (1) implies (2) we use that
![]() ${\mathcal {B}}$
is uniform while in (2) implies (1) we use the uniformity of
${\mathcal {B}}$
is uniform while in (2) implies (1) we use the uniformity of
![]() ${\mathcal {C}}$
.
${\mathcal {C}}$
.
6 Cardinal invariants associated to barriers
In this section, we define and analyze several cardinal invariants associated to barriers that play an important role in the structure of
![]() $\alpha $
-sequentially compact spaces. In particular, we extend a result in [Reference Kubiś and Szeptycki19] by showing that for every
$\alpha $
-sequentially compact spaces. In particular, we extend a result in [Reference Kubiś and Szeptycki19] by showing that for every
![]() $\alpha>1$
, the Cantor cube
$\alpha>1$
, the Cantor cube
![]() $2^\kappa $
is
$2^\kappa $
is
![]() $\alpha $
-sequentially compact if and only if
$\alpha $
-sequentially compact if and only if
![]() $\kappa <\min \{{\mathfrak {b}},{\mathfrak {s}}\}$
. When
$\kappa <\min \{{\mathfrak {b}},{\mathfrak {s}}\}$
. When
![]() $\alpha =1$
, it is known that
$\alpha =1$
, it is known that
![]() $2^\kappa $
is sequentially compact if and only if
$2^\kappa $
is sequentially compact if and only if
![]() $\kappa <{\mathfrak {s}}$
(see [Reference van Douwen11]).
$\kappa <{\mathfrak {s}}$
(see [Reference van Douwen11]).
It is also shown in [Reference Corral, Guzmán and López-Callejas7] that the cardinals
![]() ${\mathfrak {par}}_n$
are closely related to the constructions of examples of spaces that are n-sequentially compact but fail to be
${\mathfrak {par}}_n$
are closely related to the constructions of examples of spaces that are n-sequentially compact but fail to be
![]() $(n+1)$
-sequentially compact under
$(n+1)$
-sequentially compact under
![]() ${\mathfrak {s}}={\mathfrak {b}}$
. This suggests that if we aim to do similar constructions for arbitrary barriers, we should start analyzing and computing the analogous cardinal invariants for
${\mathfrak {s}}={\mathfrak {b}}$
. This suggests that if we aim to do similar constructions for arbitrary barriers, we should start analyzing and computing the analogous cardinal invariants for
![]() ${\mathfrak {par}}_n$
in arbitrary barriers. If
${\mathfrak {par}}_n$
in arbitrary barriers. If
![]() ${\mathcal {B}}$
is a barrier,
${\mathcal {B}}$
is a barrier,
![]() $\pi :{\mathcal {B}}\rightarrow 2$
, and
$\pi :{\mathcal {B}}\rightarrow 2$
, and
![]() $H\in [\omega ]^\omega $
, then we say that H is monochromatic for
$H\in [\omega ]^\omega $
, then we say that H is monochromatic for
![]() $\pi $
if
$\pi $
if
![]() $\pi $
is constant on
$\pi $
is constant on
![]() ${\mathcal {B}}|H$
. We say that H is almost monochromatic for
${\mathcal {B}}|H$
. We say that H is almost monochromatic for
![]() $\pi $
if there is
$\pi $
if there is
![]() $F\in [H]^{<\omega }$
such that
$F\in [H]^{<\omega }$
such that
![]() $H\setminus F$
is monochromatic for
$H\setminus F$
is monochromatic for
![]() $\pi $
. If
$\pi $
. If
![]() $\Pi $
is a family of colorings on
$\Pi $
is a family of colorings on
![]() ${\mathcal {B}}$
, then we say that H is almost monochromatic for
${\mathcal {B}}$
, then we say that H is almost monochromatic for
![]() $\Pi $
if it is almost monochromatic for every
$\Pi $
if it is almost monochromatic for every
![]() $\pi \in \Pi $
. We refer to
$\pi \in \Pi $
. We refer to
![]() $[\omega ]^1$
as the trivial barrier.
$[\omega ]^1$
as the trivial barrier.
Definition 6.1 If
![]() ${\mathcal {B}}$
is a barrier, then
${\mathcal {B}}$
is a barrier, then
![]() ${\mathfrak {par}}_{\mathcal {B}}$
is the minimum size of a collection of colorings on
${\mathfrak {par}}_{\mathcal {B}}$
is the minimum size of a collection of colorings on
![]() ${\mathcal {B}}$
without an almost monochromatic infinite set.
${\mathcal {B}}$
without an almost monochromatic infinite set.
If
![]() $t\in [\omega ]^{<\omega }\setminus \{\emptyset \}$
, recall that we write t as
$t\in [\omega ]^{<\omega }\setminus \{\emptyset \}$
, recall that we write t as
![]() $\{t_0,\dots ,t_{n-1}\}$
in the increasing way, and if
$\{t_0,\dots ,t_{n-1}\}$
in the increasing way, and if
![]() $I\subseteq n$
, then
$I\subseteq n$
, then
![]() $t\restriction I=\{t_i\mid i\in I\}$
. Also note that
$t\restriction I=\{t_i\mid i\in I\}$
. Also note that
![]() $t\restriction 2\sqsubseteq t$
for
$t\restriction 2\sqsubseteq t$
for
![]() $n\geq 2$
. Given a barrier
$n\geq 2$
. Given a barrier
![]() ${\mathcal {B}}$
such that each of its elements has size at least
${\mathcal {B}}$
such that each of its elements has size at least
![]() $2$
, if we let
$2$
, if we let
![]() ${\mathcal {B}}\restriction 2:=\{t\restriction 2: t\in {\mathcal {B}}\}$
, then
${\mathcal {B}}\restriction 2:=\{t\restriction 2: t\in {\mathcal {B}}\}$
, then
![]() ${\mathcal {B}}\restriction 2=[\omega ]^2$
. For
${\mathcal {B}}\restriction 2=[\omega ]^2$
. For
![]() $n\in \omega $
, the cardinal
$n\in \omega $
, the cardinal
![]() ${\mathfrak {par}}_n$
mentioned above is exactly
${\mathfrak {par}}_n$
mentioned above is exactly
![]() ${\mathfrak {par}}_{[\omega ]^n}$
, so we will stick with the classical terminology
${\mathfrak {par}}_{[\omega ]^n}$
, so we will stick with the classical terminology
![]() ${\mathfrak {par}}_n$
when
${\mathfrak {par}}_n$
when
![]() ${\mathcal {B}}=[\omega ]^n$
.
${\mathcal {B}}=[\omega ]^n$
.
Theorem 6.2 If
![]() ${\mathcal {B}}$
is a nontrivial barrier, then
${\mathcal {B}}$
is a nontrivial barrier, then
![]() ${\mathfrak {par}}_{\mathcal {B}}\leq {\mathfrak {par}}_2$
.
${\mathfrak {par}}_{\mathcal {B}}\leq {\mathfrak {par}}_2$
.
Proof As
![]() ${\mathcal {B}}$
is a nontrivial barrier, there is
${\mathcal {B}}$
is a nontrivial barrier, there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() ${\mathcal {B}}|(\omega \setminus n)$
has all of its elements of size at least two. Without loss of generality, we may assume that
${\mathcal {B}}|(\omega \setminus n)$
has all of its elements of size at least two. Without loss of generality, we may assume that
![]() $n=0$
. Let
$n=0$
. Let
![]() $\Pi =\{\pi _\alpha \mid \alpha \in {\mathfrak {par}}_2\}$
be a family of colorings on
$\Pi =\{\pi _\alpha \mid \alpha \in {\mathfrak {par}}_2\}$
be a family of colorings on
![]() $[\omega ]^2$
with no almost monochromatic infinite sets. Define
$[\omega ]^2$
with no almost monochromatic infinite sets. Define
![]() $\widehat {\pi }_\alpha :{\mathcal {B}}\rightarrow 2$
for every
$\widehat {\pi }_\alpha :{\mathcal {B}}\rightarrow 2$
for every
![]() $\alpha \in {\mathfrak {par}}_2$
, given by
$\alpha \in {\mathfrak {par}}_2$
, given by
![]() $\widehat {\pi }_\alpha (t)=\pi _\alpha (t\restriction 2)$
. Note that if H is a an almost monochromatic infinite set for
$\widehat {\pi }_\alpha (t)=\pi _\alpha (t\restriction 2)$
. Note that if H is a an almost monochromatic infinite set for
![]() $\widehat {\Pi }=\{\widehat {\pi }_\alpha \mid \alpha \in {\mathfrak {par}}_2\}$
, then H is also an almost monochromatic infinite set for
$\widehat {\Pi }=\{\widehat {\pi }_\alpha \mid \alpha \in {\mathfrak {par}}_2\}$
, then H is also an almost monochromatic infinite set for
![]() $\Pi $
. Hence,
$\Pi $
. Hence,
![]() $\widehat \Pi $
has no infinite almost monochromatic sets.
$\widehat \Pi $
has no infinite almost monochromatic sets.
Recall that if
![]() ${\mathcal {B}}$
is a barrier, the rank of
${\mathcal {B}}$
is a barrier, the rank of
![]() ${\mathcal {B}}[n]$
is strictly smaller than the rank of
${\mathcal {B}}[n]$
is strictly smaller than the rank of
![]() ${\mathcal {B}}$
for every
${\mathcal {B}}$
for every
![]() $n\in \omega $
. This allows us to show that the same idea that proves that
$n\in \omega $
. This allows us to show that the same idea that proves that
![]() ${\mathfrak {par}}_n=\min \{{\mathfrak {b}},{\mathfrak {s}}\}$
for every
${\mathfrak {par}}_n=\min \{{\mathfrak {b}},{\mathfrak {s}}\}$
for every
![]() $n\in \omega $
in [Reference Blass2] also works for arbitrary barriers.
$n\in \omega $
in [Reference Blass2] also works for arbitrary barriers.
Theorem 6.3 If
![]() ${\mathcal {B}}$
is a barrier such that each of its elements has size at least
${\mathcal {B}}$
is a barrier such that each of its elements has size at least
![]() $2$
, then
$2$
, then
![]() ${\mathfrak {par}}_{\mathcal {B}}\geq {\mathfrak {par}}_2$
.
${\mathfrak {par}}_{\mathcal {B}}\geq {\mathfrak {par}}_2$
.
Proof By induction on the rank of
![]() ${\mathcal {B}}$
. Suppose that
${\mathcal {B}}$
. Suppose that
![]() ${\mathcal {B}}$
has rank
${\mathcal {B}}$
has rank
![]() $\gamma $
and the result is true for every barrier of rank strictly smaller than
$\gamma $
and the result is true for every barrier of rank strictly smaller than
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $\kappa <{\mathfrak {par}}_2$
and let
$\kappa <{\mathfrak {par}}_2$
and let
![]() $\{\pi _\alpha :\alpha \in \kappa \}$
be a set of colorings on
$\{\pi _\alpha :\alpha \in \kappa \}$
be a set of colorings on
![]() ${\mathcal {B}}$
. We are going to show that there exists an almost monochromatic infinite set for this family.
${\mathcal {B}}$
. We are going to show that there exists an almost monochromatic infinite set for this family.
For every
![]() $\alpha \in \kappa $
and every
$\alpha \in \kappa $
and every
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $\pi _\alpha ^n={\mathcal {B}}[n]\rightarrow 2$
given by
$\pi _\alpha ^n={\mathcal {B}}[n]\rightarrow 2$
given by
![]() $\pi _\alpha ^n(s)=\pi _\alpha (\{n\}\cup s)$
.
$\pi _\alpha ^n(s)=\pi _\alpha (\{n\}\cup s)$
.
We recursively construct a collection
![]() $\{H_n: n\in \omega \}\subseteq [\omega ]^\omega $
such that
$\{H_n: n\in \omega \}\subseteq [\omega ]^\omega $
such that
-
(1)
 $H_{n+1}\in [H_n]^\omega $
.
$H_{n+1}\in [H_n]^\omega $
. -
(2)
 $H_{n+1}$
is almost monochromatic for
$H_{n+1}$
is almost monochromatic for
 $\{\pi _\alpha ^n\restriction ({\mathcal {B}}[n]| H_{n}): \alpha \in \kappa \}$
$\{\pi _\alpha ^n\restriction ({\mathcal {B}}[n]| H_{n}): \alpha \in \kappa \}$
We start by defining
![]() $H_0=\omega \setminus 1$
, and as
$H_0=\omega \setminus 1$
, and as
![]() $B[0]$
has rank smaller than
$B[0]$
has rank smaller than
![]() $\gamma $
, by our inductive hypothesis, we know that there is
$\gamma $
, by our inductive hypothesis, we know that there is
![]() $H_1\in [\omega \setminus 1]^\omega $
such that
$H_1\in [\omega \setminus 1]^\omega $
such that
![]() $H_1$
is almost monochromatic for
$H_1$
is almost monochromatic for
![]() $\{\pi _\alpha ^0\mid \alpha \in \kappa \}$
. Now suppose that we have already defined
$\{\pi _\alpha ^0\mid \alpha \in \kappa \}$
. Now suppose that we have already defined
![]() $H_n$
and consider the family
$H_n$
and consider the family
![]() $\{\pi _\alpha ^n\restriction ({\mathcal {B}}[n]|H_n): \alpha \in \kappa \}$
. As
$\{\pi _\alpha ^n\restriction ({\mathcal {B}}[n]|H_n): \alpha \in \kappa \}$
. As
![]() ${\mathcal {B}}[n]|H_n$
has also rank smaller than
${\mathcal {B}}[n]|H_n$
has also rank smaller than
![]() $\gamma $
, there is
$\gamma $
, there is
![]() $H_{n+1}\in [H_n]^\omega $
such that
$H_{n+1}\in [H_n]^\omega $
such that
![]() $H_{n+1}$
is almost monochromatic for this family.
$H_{n+1}$
is almost monochromatic for this family.
Take H an infinite pseudointersection of
![]() $\{H_n: n\in \omega \}$
. Note for every
$\{H_n: n\in \omega \}$
. Note for every
![]() $n\in H$
and every
$n\in H$
and every
![]() $\alpha \in \kappa $
, we have that
$\alpha \in \kappa $
, we have that
![]() $H_n$
is almost monochromatic for
$H_n$
is almost monochromatic for
![]() $\pi _\alpha ^n$
with color
$\pi _\alpha ^n$
with color
![]() $j(\alpha ,n)\in \{0,1\}$
. For every
$j(\alpha ,n)\in \{0,1\}$
. For every
![]() $\alpha \in \kappa $
, define an increasing
$\alpha \in \kappa $
, define an increasing
![]() $f_\alpha \in H^\omega $
such that
$f_\alpha \in H^\omega $
such that
![]() $H_n\setminus f_\alpha (n)$
is monochromatic for
$H_n\setminus f_\alpha (n)$
is monochromatic for
![]() $\pi _\alpha ^n$
. Also let
$\pi _\alpha ^n$
. Also let
![]() $g\in \omega ^\omega $
be increasing such that
$g\in \omega ^\omega $
be increasing such that
![]() $H\setminus g(n)\subseteq H_n$
. As
$H\setminus g(n)\subseteq H_n$
. As
![]() ${\mathcal {F}}=\{f_\alpha :\alpha \in \kappa \}\cup \{g\}\subseteq \omega ^\omega $
has size less than
${\mathcal {F}}=\{f_\alpha :\alpha \in \kappa \}\cup \{g\}\subseteq \omega ^\omega $
has size less than
![]() ${\mathfrak {par}}_2\leq {\mathfrak {b}}$
, there exists
${\mathfrak {par}}_2\leq {\mathfrak {b}}$
, there exists
![]() $f\in \omega ^\omega $
strictly increasing that dominates
$f\in \omega ^\omega $
strictly increasing that dominates
![]() ${\mathcal {F}}$
.
${\mathcal {F}}$
.
For every
![]() $i\in 2$
, let
$i\in 2$
, let
![]() $X_\alpha ^i:=\{n\in H: j(\alpha ,n)=i\}$
. Note that
$X_\alpha ^i:=\{n\in H: j(\alpha ,n)=i\}$
. Note that
![]() $\{X_\alpha ^0\mid \alpha \in \kappa \}$
is a collection of less than
$\{X_\alpha ^0\mid \alpha \in \kappa \}$
is a collection of less than
![]() ${\mathfrak {par}}_2\leq {\mathfrak {s}}$
subsets of H, so there is
${\mathfrak {par}}_2\leq {\mathfrak {s}}$
subsets of H, so there is
![]() $X\in [H]^\omega $
such that for every
$X\in [H]^\omega $
such that for every
![]() $\alpha \in \kappa $
, there is
$\alpha \in \kappa $
, there is
![]() $j(\alpha )\in \{0,1\}$
such that
$j(\alpha )\in \{0,1\}$
such that
![]() $X\subseteq ^* X_\alpha ^{j(\alpha )}$
.
$X\subseteq ^* X_\alpha ^{j(\alpha )}$
.
Let us define
![]() $J:=\{x_n\mid n\in \omega \}\subseteq X\subseteq H$
such that
$J:=\{x_n\mid n\in \omega \}\subseteq X\subseteq H$
such that
![]() $x_{n+1}>f(x_n)$
for every
$x_{n+1}>f(x_n)$
for every
![]() $n\in \omega $
.
$n\in \omega $
.
Claim:
J is almost monochromatic for
![]() $\{\pi _\alpha \mid \alpha \in \kappa \}$
.
$\{\pi _\alpha \mid \alpha \in \kappa \}$
.
Proof of the claim
Let
![]() $\alpha \in \kappa $
. We know that
$\alpha \in \kappa $
. We know that
![]() $X\subseteq ^* X_\alpha ^{j(\alpha )}$
,
$X\subseteq ^* X_\alpha ^{j(\alpha )}$
,
![]() $f_\alpha <^*f$
, and
$f_\alpha <^*f$
, and
![]() $g<^* f$
, so there exists
$g<^* f$
, so there exists
![]() $k\in \omega $
such that
$k\in \omega $
such that
-
(1)
 $X\setminus k\subseteq X_\alpha ^{j(\alpha )}$
,
$X\setminus k\subseteq X_\alpha ^{j(\alpha )}$
, -
(2)
 $f_\alpha (n)<f(n)$
for every
$f_\alpha (n)<f(n)$
for every
 $n>k$
, and
$n>k$
, and -
(3)
 $g(n)<f(n)$
for every
$g(n)<f(n)$
for every
 $n>k$
.
$n>k$
.
Fix
![]() $s\in {\mathcal {B}}|(J\setminus (k+1))$
and let
$s\in {\mathcal {B}}|(J\setminus (k+1))$
and let
![]() $n=\min (s)$
and
$n=\min (s)$
and
![]() $t=s\setminus \{n\}$
. Then, we have that
$t=s\setminus \{n\}$
. Then, we have that
![]() $n\in X_\alpha ^{j(\alpha )}$
and
$n\in X_\alpha ^{j(\alpha )}$
and
Notice that
![]() $\min (t)>f(n)>f_\alpha (n)$
; hence,
$\min (t)>f(n)>f_\alpha (n)$
; hence,
![]() $t\subseteq H_n\setminus f_\alpha (n)$
. But then,
$t\subseteq H_n\setminus f_\alpha (n)$
. But then,
![]() $\pi _\alpha (s)=\pi _\alpha ^n(t)=j(\alpha ,n)$
and
$\pi _\alpha (s)=\pi _\alpha ^n(t)=j(\alpha ,n)$
and
![]() $j(\alpha ,n)=j(\alpha )$
since
$j(\alpha ,n)=j(\alpha )$
since
![]() $n\in X_\alpha ^{j(\alpha )}$
. This proves that
$n\in X_\alpha ^{j(\alpha )}$
. This proves that
![]() $\pi _\alpha $
is constant on
$\pi _\alpha $
is constant on
![]() ${\mathcal {B}}|(J\setminus (k+1))$
with color
${\mathcal {B}}|(J\setminus (k+1))$
with color
![]() $j(\alpha )$
.
$j(\alpha )$
.
The proof of the previous claim finishes the proof of the theorem.
Corollary 6.4
![]() ${\mathfrak {par}}_{\mathcal {B}}={\mathfrak {par}}_2$
for every nontrivial barrier
${\mathfrak {par}}_{\mathcal {B}}={\mathfrak {par}}_2$
for every nontrivial barrier
![]() ${\mathcal {B}}$
on
${\mathcal {B}}$
on
![]() $\omega $
and
$\omega $
and
![]() ${\mathfrak {par}}_{[\omega ]^1}={\mathfrak {s}}$
.
${\mathfrak {par}}_{[\omega ]^1}={\mathfrak {s}}$
.
Corollary 6.5 If
![]() $\kappa <{\mathfrak {par}}_2$
and
$\kappa <{\mathfrak {par}}_2$
and
![]() ${\mathcal {B}}$
is a barrier, then
${\mathcal {B}}$
is a barrier, then
![]() $2^\kappa $
is
$2^\kappa $
is
![]() ${\mathcal {B}}$
-sequentially compact. Moreover,
${\mathcal {B}}$
-sequentially compact. Moreover,
for every nontrivial barrier
![]() ${\mathcal {B}}$
.
${\mathcal {B}}$
.
Proof If
![]() $\kappa <{\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}_2=\min \{{\mathfrak {s}},{\mathfrak {b}}\}$
, then
$\kappa <{\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}_2=\min \{{\mathfrak {s}},{\mathfrak {b}}\}$
, then
![]() $\kappa <{\mathfrak {s}}$
and so
$\kappa <{\mathfrak {s}}$
and so
![]() $2^\kappa $
is sequentially compact. Similarly, it has character less than
$2^\kappa $
is sequentially compact. Similarly, it has character less than
![]() ${\mathfrak {b}}$
since
${\mathfrak {b}}$
since
![]() $\kappa <{\mathfrak {b}}$
. Therefore,
$\kappa <{\mathfrak {b}}$
. Therefore,
![]() $2^\kappa $
is
$2^\kappa $
is
![]() $\omega _1$
-sequentially compact by Theorem 4.2. Conversely,
$\omega _1$
-sequentially compact by Theorem 4.2. Conversely,
![]() $2^{{\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}_2}$
is not even
$2^{{\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}_2}$
is not even
![]() $2$
-sequentially compact by a result in [Reference Kubiś and Szeptycki19].
$2$
-sequentially compact by a result in [Reference Kubiś and Szeptycki19].
The dual cardinal to
![]() ${\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}$
is the cardinal
${\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}$
is the cardinal
![]() ${\mathfrak {hom}}$
. The characterization of
${\mathfrak {hom}}$
. The characterization of
![]() ${\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}$
in terms of
${\mathfrak {p}}{\mathfrak {a}}{\mathfrak {r}}$
in terms of
![]() ${\mathfrak {b}}$
and
${\mathfrak {b}}$
and
![]() ${\mathfrak {s}}$
has also a dual version using
${\mathfrak {s}}$
has also a dual version using
![]() ${\mathfrak {d}}$
and a variant of
${\mathfrak {d}}$
and a variant of
![]() ${\mathfrak {r}}$
, the dual cardinals of
${\mathfrak {r}}$
, the dual cardinals of
![]() ${\mathfrak {b}}$
and
${\mathfrak {b}}$
and
![]() ${\mathfrak {s}}$
, respectively (see [Reference Blass2]).
${\mathfrak {s}}$
, respectively (see [Reference Blass2]).
Notation 6.6 Let N be a countable set,
![]() ${\mathcal {I}}$
an ideal on N, and
${\mathcal {I}}$
an ideal on N, and
![]() $X,Y\subseteq N$
. Then,
$X,Y\subseteq N$
. Then,
![]() $X\subseteq _{\mathcal {I}} Y$
means that
$X\subseteq _{\mathcal {I}} Y$
means that
![]() $X\setminus Y\in {\mathcal {I}}$
.
$X\setminus Y\in {\mathcal {I}}$
.
Definition 6.7 Given a barrier
![]() ${\mathcal {B}}$
let,
${\mathcal {B}}$
let,
and
A family as in the definition of
![]() ${\mathfrak {hom}}_{\mathcal {B}}$
is called a homogeneous family for
${\mathfrak {hom}}_{\mathcal {B}}$
is called a homogeneous family for
![]() ${\mathcal {B}}$
or a
${\mathcal {B}}$
or a
![]() ${\mathcal {B}}$
-homogeneous family. Analogously, a family as in the definition of
${\mathcal {B}}$
-homogeneous family. Analogously, a family as in the definition of
![]() ${\mathfrak {r}}_{\mathcal {B}}$
is called a reaping family for
${\mathfrak {r}}_{\mathcal {B}}$
is called a reaping family for
![]() ${\mathcal {B}}$
or a
${\mathcal {B}}$
or a
![]() ${\mathcal {B}}$
-reaping family.
${\mathcal {B}}$
-reaping family.
Recall that by the Nash-Williams theorem, for every
![]() $\pi :{\mathcal {B}}\rightarrow 2$
, there is
$\pi :{\mathcal {B}}\rightarrow 2$
, there is
![]() $M\in [\omega ]^\omega $
such that
$M\in [\omega ]^\omega $
such that
![]() $\pi \restriction ({\mathcal {B}}|M)$
is constant. In this way,
$\pi \restriction ({\mathcal {B}}|M)$
is constant. In this way,
![]() ${\mathfrak {hom}}_{\mathcal {B}}$
is well-defined, and
${\mathfrak {hom}}_{\mathcal {B}}$
is well-defined, and
![]() ${\mathfrak {r}}_{\mathcal {B}}\leq {\mathfrak {hom}}_{\mathcal {B}}$
since every
${\mathfrak {r}}_{\mathcal {B}}\leq {\mathfrak {hom}}_{\mathcal {B}}$
since every
![]() ${\mathcal {B}}$
-homogeneous family is a
${\mathcal {B}}$
-homogeneous family is a
![]() ${\mathcal {B}}$
-reaping family. In particular,
${\mathcal {B}}$
-reaping family. In particular,
![]() ${\mathfrak {r}}_{\mathcal {B}}$
is well-defined.
${\mathfrak {r}}_{\mathcal {B}}$
is well-defined.
Note that if
![]() ${\mathcal {B}}$
is the trivial barrier (i.e.,
${\mathcal {B}}$
is the trivial barrier (i.e.,
![]() ${\mathcal {B}}=[\omega ]^1$
), then
${\mathcal {B}}=[\omega ]^1$
), then
![]() ${\mathfrak {r}}_{\mathcal {B}}={\mathfrak {hom}}_{\mathcal {B}}={\mathfrak {r}}$
. However, if
${\mathfrak {r}}_{\mathcal {B}}={\mathfrak {hom}}_{\mathcal {B}}={\mathfrak {r}}$
. However, if
![]() ${\mathcal {B}}$
is a nontrivial barrier, then
${\mathcal {B}}$
is a nontrivial barrier, then
![]() ${\mathfrak {hom}}_2\leq {\mathfrak {hom}}_{\mathcal {B}}$
. To see this, we can suppose that every element of
${\mathfrak {hom}}_2\leq {\mathfrak {hom}}_{\mathcal {B}}$
. To see this, we can suppose that every element of
![]() ${\mathcal {B}}$
has size at least
${\mathcal {B}}$
has size at least
![]() $2$
, and thus, every coloring
$2$
, and thus, every coloring
![]() $\pi :[\omega ]^2\rightarrow 2$
induces a coloring of
$\pi :[\omega ]^2\rightarrow 2$
induces a coloring of
![]() $\hat {\pi }:{\mathcal {B}}\rightarrow 2$
given by
$\hat {\pi }:{\mathcal {B}}\rightarrow 2$
given by
![]() $\hat {\pi }(s)=\pi (s\restriction 2)$
. Now an infinite homogeneous set for
$\hat {\pi }(s)=\pi (s\restriction 2)$
. Now an infinite homogeneous set for
![]() $\hat {\pi }$
is also homogeneous for
$\hat {\pi }$
is also homogeneous for
![]() $\pi $
, which in turn gives that any homogeneous family for
$\pi $
, which in turn gives that any homogeneous family for
![]() ${\mathcal {B}}$
is a homogeneous family for
${\mathcal {B}}$
is a homogeneous family for
![]() $[\omega ]^2$
, and then,
$[\omega ]^2$
, and then,
![]() $\max \{{\mathfrak {d}},{\mathfrak {r}}_\sigma \}={\mathfrak {hom}}_2\leq {\mathfrak {hom}}_{\mathcal {B}}$
. In particular,
$\max \{{\mathfrak {d}},{\mathfrak {r}}_\sigma \}={\mathfrak {hom}}_2\leq {\mathfrak {hom}}_{\mathcal {B}}$
. In particular,
![]() ${\mathfrak {d}}\leq {\mathfrak {hom}}_{\mathcal {B}}$
. Ramsey ultrafilters will be helpful in our study of the cardinal
${\mathfrak {d}}\leq {\mathfrak {hom}}_{\mathcal {B}}$
. Ramsey ultrafilters will be helpful in our study of the cardinal
![]() ${\mathfrak {hom}}_{\mathcal {B}}$
.
${\mathfrak {hom}}_{\mathcal {B}}$
.
Recall that a nonprincipal ultrafilter
![]() ${\mathcal {U}}$
on
${\mathcal {U}}$
on
![]() $\omega $
is Ramsey if for all
$\omega $
is Ramsey if for all
![]() $\pi :[\omega ]^2\rightarrow 2$
, there is
$\pi :[\omega ]^2\rightarrow 2$
, there is
![]() $U\in {\mathcal {U}}$
such that
$U\in {\mathcal {U}}$
such that
![]() $\pi \restriction [U]^2$
is constant. A family
$\pi \restriction [U]^2$
is constant. A family
![]() ${\mathcal {F}}\subseteq [\omega ]^\omega $
is selective if for every decreasing sequence
${\mathcal {F}}\subseteq [\omega ]^\omega $
is selective if for every decreasing sequence
![]() $\{Y_n\mid n\in \omega \}\subseteq {\mathcal {F}}$
, there is
$\{Y_n\mid n\in \omega \}\subseteq {\mathcal {F}}$
, there is
![]() $f:\omega \rightarrow \omega $
such that
$f:\omega \rightarrow \omega $
such that
![]() $f[\omega ]\in {\mathcal {F}}$
,
$f[\omega ]\in {\mathcal {F}}$
,
![]() $f(0)\in Y_0$
, and
$f(0)\in Y_0$
, and
![]() $f(n+1)\in Y_{f(n)}$
for all
$f(n+1)\in Y_{f(n)}$
for all
![]() $n\in \omega $
. The following result, which according to D. Booth is mostly due to K. Kunen, relates Ramsey ultrafilters and selective families.
$n\in \omega $
. The following result, which according to D. Booth is mostly due to K. Kunen, relates Ramsey ultrafilters and selective families.
Theorem 6.8 [Reference Booth4] If
![]() ${\mathcal {U}}$
is a nonprincipal ultrafilter, then
${\mathcal {U}}$
is a nonprincipal ultrafilter, then
![]() ${\mathcal {U}}$
is Ramsey if and only if it is selective.
${\mathcal {U}}$
is Ramsey if and only if it is selective.
We will show now that a base for a Ramsey ultrafilter is a homogeneous family for every barrier
![]() ${\mathcal {B}}$
. Hence, if we define
${\mathcal {B}}$
. Hence, if we define
![]() ${\mathfrak {u}}_R$
as the minimum character of a Ramsey ultrafilter,Footnote
1
we get that
${\mathfrak {u}}_R$
as the minimum character of a Ramsey ultrafilter,Footnote
1
we get that
![]() ${\mathfrak {hom}}_{\mathcal {B}}\leq {\mathfrak {u}}_R$
.
${\mathfrak {hom}}_{\mathcal {B}}\leq {\mathfrak {u}}_R$
.
The next theorem is a standard result of Local Ramsey theory (see [Reference Todorčević26] Chapter 7). It follows immediately from Theorem 7.42 in [Reference Todorčević26] in the same way Nash-Williams’ theorem follows from Ellentuck theorem. For the convenience of reader, we sketch the argument.
Theorem 6.9 If
![]() ${\mathcal {U}}$
is a Ramsey ultrafilter,
${\mathcal {U}}$
is a Ramsey ultrafilter,
![]() ${\mathcal {B}}$
is a barrier on
${\mathcal {B}}$
is a barrier on
![]() $\omega $
, and
$\omega $
, and
![]() $\pi :{\mathcal {B}}\rightarrow 2$
, then there is
$\pi :{\mathcal {B}}\rightarrow 2$
, then there is
![]() $U\in {\mathcal {U}}$
such that
$U\in {\mathcal {U}}$
such that
![]() $\pi \restriction ({\mathcal {B}}|U)$
is constant.
$\pi \restriction ({\mathcal {B}}|U)$
is constant.
Proof By induction on the rank of the barrier. If
![]() ${\mathcal {B}}$
has rank zero (i.e,
${\mathcal {B}}$
has rank zero (i.e,
![]() ${\mathcal {B}}=\{\emptyset \}$
), then the result is trivial.
${\mathcal {B}}=\{\emptyset \}$
), then the result is trivial.
Suppose that
![]() ${\mathcal {B}}$
has rank
${\mathcal {B}}$
has rank
![]() $\gamma $
and the result is true for every barrier of rank smaller than
$\gamma $
and the result is true for every barrier of rank smaller than
![]() $\gamma $
. As
$\gamma $
. As
![]() $B[n]$
is a barrier on
$B[n]$
is a barrier on
![]() $\omega \setminus (n+1)$
of rank less than
$\omega \setminus (n+1)$
of rank less than
![]() $\gamma $
, there is
$\gamma $
, there is
![]() $V_n\in {\mathcal {U}}$
such that the coloring
$V_n\in {\mathcal {U}}$
such that the coloring
![]() $\pi _n:B[n]\rightarrow 2$
is constant on
$\pi _n:B[n]\rightarrow 2$
is constant on
![]() ${\mathcal {B}}[n]|V_n$
, where
${\mathcal {B}}[n]|V_n$
, where
![]() $\pi _n(s)=\pi (\{n\}\cup s)$
.
$\pi _n(s)=\pi (\{n\}\cup s)$
.
For every
![]() $n\in \omega $
, we know that
$n\in \omega $
, we know that
![]() $\pi _n\restriction ({\mathcal {B}}[n]|V_n)$
is constant on color
$\pi _n\restriction ({\mathcal {B}}[n]|V_n)$
is constant on color
![]() $j(n)\in 2$
. So take
$j(n)\in 2$
. So take
![]() $V\in {\mathcal {U}}$
and
$V\in {\mathcal {U}}$
and
![]() $i\in 2$
such that
$i\in 2$
such that
![]() $j(n)=i$
for all
$j(n)=i$
for all
![]() $n\in V$
.
$n\in V$
.
Now call
![]() $U_n=(\bigcap _{m\leq n}V_n)\cap V \cap (\omega \setminus n+1)$
and note that
$U_n=(\bigcap _{m\leq n}V_n)\cap V \cap (\omega \setminus n+1)$
and note that
![]() $\{U_n\mid n\in \omega \}$
is a decreasing sequence of elements of
$\{U_n\mid n\in \omega \}$
is a decreasing sequence of elements of
![]() ${\mathcal {U}}$
, so applying that
${\mathcal {U}}$
, so applying that
![]() ${\mathcal {U}}$
is selective, there is
${\mathcal {U}}$
is selective, there is
![]() $f\in \omega ^\omega $
such that
$f\in \omega ^\omega $
such that
![]() $f[\omega ]\in {\mathcal {U}}$
,
$f[\omega ]\in {\mathcal {U}}$
,
![]() $f(0)\in U_0$
, and
$f(0)\in U_0$
, and
![]() $f(n+1)\in U_{f(n)}$
for all
$f(n+1)\in U_{f(n)}$
for all
![]() $n\in \omega $
. Define
$n\in \omega $
. Define
![]() $U:=f[\omega ]$
.
$U:=f[\omega ]$
.
It remains to show that
![]() $\pi \restriction ({\mathcal {B}}|U)$
is constant with value i. Indeed, let
$\pi \restriction ({\mathcal {B}}|U)$
is constant with value i. Indeed, let
![]() ${s=\{a_0,\dots ,a_k\}\in {\mathcal {B}}|U}$
. Then,
${s=\{a_0,\dots ,a_k\}\in {\mathcal {B}}|U}$
. Then,
![]() $a_0\in V$
and
$a_0\in V$
and
so that
![]() $\{a_1,\dots ,a_k\}\in {\mathcal {B}}[a_0]|V_{a_0},$
. Then,
$\{a_1,\dots ,a_k\}\in {\mathcal {B}}[a_0]|V_{a_0},$
. Then,
![]() $\pi (s)=\pi _{a_0}(\{a_1,\dots ,a_k\})=j(a_0)=i$
.
$\pi (s)=\pi _{a_0}(\{a_1,\dots ,a_k\})=j(a_0)=i$
.
Notation 6.10 If
![]() $R\in [\omega ]^\omega $
, then
$R\in [\omega ]^\omega $
, then
![]() ${\mathbb {H}}(R)$
is the collection of all nonempty trees
${\mathbb {H}}(R)$
is the collection of all nonempty trees
![]() $T\subseteq R^{<\omega }$
such that
$T\subseteq R^{<\omega }$
such that
![]() $\mathrm{succ}_T(s)$
is cofinite in R for all
$\mathrm{succ}_T(s)$
is cofinite in R for all
![]() $s\in T$
.
$s\in T$
.
We will need the following folklore facts.
Proposition 6.11 If
![]() $R\in [\omega ]^\omega $
and
$R\in [\omega ]^\omega $
and
![]() $T\in {\mathbb {H}}(R)$
, then there is
$T\in {\mathbb {H}}(R)$
, then there is
![]() $A\in [R]^\omega $
such that
$A\in [R]^\omega $
such that
![]() ${[A]^\omega \subseteq [T]}$
.
${[A]^\omega \subseteq [T]}$
.
Proposition 6.12
![]() $\mathsf {cof}({\mathsf {FIN}}^{\mathcal {B}})={\mathfrak {d}}$
for every nontrivial barrier
$\mathsf {cof}({\mathsf {FIN}}^{\mathcal {B}})={\mathfrak {d}}$
for every nontrivial barrier
![]() ${\mathcal {B}}$
.
${\mathcal {B}}$
.
An explicit proof for the previous result about
![]() $\mathsf {cof}({\mathsf {FIN}}^{\mathcal {B}})$
, where
$\mathsf {cof}({\mathsf {FIN}}^{\mathcal {B}})$
, where
![]() ${\mathcal {B}}$
is a barrier of finite rank, appears in [Reference Corral, Guzmán and López-Callejas7]. The same argument works for general barriers.
${\mathcal {B}}$
is a barrier of finite rank, appears in [Reference Corral, Guzmán and López-Callejas7]. The same argument works for general barriers.
Theorem 6.13
![]() ${\mathfrak {hom}}_{\mathcal {B}}=\max \{{\mathfrak {d}},{\mathfrak {r}}_{\mathcal {B}}\}$
for every nontrivial barrier
${\mathfrak {hom}}_{\mathcal {B}}=\max \{{\mathfrak {d}},{\mathfrak {r}}_{\mathcal {B}}\}$
for every nontrivial barrier
![]() ${\mathcal {B}}$
on
${\mathcal {B}}$
on
![]() $\omega $
.
$\omega $
.
Proof We already noted that
![]() $\max \{{\mathfrak {d}},{\mathfrak {r}}_{\mathcal {B}}\}\leq {\mathfrak {hom}}_{\mathcal {B}}$
, so it is enough to prove the other inequality. For this, let
$\max \{{\mathfrak {d}},{\mathfrak {r}}_{\mathcal {B}}\}\leq {\mathfrak {hom}}_{\mathcal {B}}$
, so it is enough to prove the other inequality. For this, let
![]() ${\mathcal {R}}=\{R_\beta \mid \beta \in {\mathfrak {r}}_{\mathcal {B}}\}$
be a reaping family for
${\mathcal {R}}=\{R_\beta \mid \beta \in {\mathfrak {r}}_{\mathcal {B}}\}$
be a reaping family for
![]() ${\mathcal {B}}$
, and for every
${\mathcal {B}}$
, and for every
![]() ${\beta \in {\mathfrak {r}}_{\mathcal {B}}}$
, let
${\beta \in {\mathfrak {r}}_{\mathcal {B}}}$
, let
![]() $\{X_\alpha ^\beta \mid \alpha \in {\mathfrak {d}}\}$
cofinal in
$\{X_\alpha ^\beta \mid \alpha \in {\mathfrak {d}}\}$
cofinal in
![]() ${\mathsf {FIN}}^{{\mathcal {B}}|R_\beta }$
. Now by definition of
${\mathsf {FIN}}^{{\mathcal {B}}|R_\beta }$
. Now by definition of
![]() ${\mathsf {FIN}}^{{\mathcal {B}}|R_\beta }$
and Proposition 6.11, for every
${\mathsf {FIN}}^{{\mathcal {B}}|R_\beta }$
and Proposition 6.11, for every
![]() $\beta \in {\mathfrak {r}}_{\mathcal {B}}$
and every
$\beta \in {\mathfrak {r}}_{\mathcal {B}}$
and every
![]() $\alpha \in {\mathfrak {d}}$
, there are
$\alpha \in {\mathfrak {d}}$
, there are
![]() $T_\alpha ^\beta \in {\mathbb {H}}(R_\beta )$
and
$T_\alpha ^\beta \in {\mathbb {H}}(R_\beta )$
and
![]() ${A_\alpha ^\beta \in [R_\beta ]^\omega }$
such that
${A_\alpha ^\beta \in [R_\beta ]^\omega }$
such that
-
(1)
 $T_\alpha ^\beta \cap X_\alpha ^\beta =\emptyset $
,
$T_\alpha ^\beta \cap X_\alpha ^\beta =\emptyset $
, -
(2)
 $[A_\alpha ^\beta ]^\omega \subseteq [T_\alpha ^\beta ]$
.
$[A_\alpha ^\beta ]^\omega \subseteq [T_\alpha ^\beta ]$
.
Now let
![]() ${\mathcal {H}}= \{A_\alpha ^\beta \mid \beta \in {\mathfrak {r}}_\beta \wedge \alpha \in {\mathfrak {d}}\}$
. We claim that
${\mathcal {H}}= \{A_\alpha ^\beta \mid \beta \in {\mathfrak {r}}_\beta \wedge \alpha \in {\mathfrak {d}}\}$
. We claim that
![]() ${\mathcal {H}}$
is a homogeneous family for
${\mathcal {H}}$
is a homogeneous family for
![]() ${\mathcal {B}}$
. To see this, let
${\mathcal {B}}$
. To see this, let
![]() $S\subseteq {\mathcal {B}}$
. As
$S\subseteq {\mathcal {B}}$
. As
![]() ${\mathcal {R}}$
is a reaping family for
${\mathcal {R}}$
is a reaping family for
![]() ${\mathcal {B}}$
, there is
${\mathcal {B}}$
, there is
![]() $\beta \in {\mathfrak {r}}_\beta $
and
$\beta \in {\mathfrak {r}}_\beta $
and
![]() $i\in 2$
such that
$i\in 2$
such that
![]() ${\mathcal {B}}|R_\beta \subseteq _{{\mathsf {FIN}}^{\mathcal {B}}}S^i$
. Now call
${\mathcal {B}}|R_\beta \subseteq _{{\mathsf {FIN}}^{\mathcal {B}}}S^i$
. Now call
![]() $X:=({\mathcal {B}}|R_\beta )\setminus S^i\in {\mathsf {FIN}}^{\mathcal {B}}$
. Moreover, as
$X:=({\mathcal {B}}|R_\beta )\setminus S^i\in {\mathsf {FIN}}^{\mathcal {B}}$
. Moreover, as
![]() $X\subseteq {\mathcal {B}}|R_\beta $
, then
$X\subseteq {\mathcal {B}}|R_\beta $
, then
![]() $X\in {\mathsf {FIN}}^{{\mathcal {B}}|R_\beta }$
. Thus, there is
$X\in {\mathsf {FIN}}^{{\mathcal {B}}|R_\beta }$
. Thus, there is
![]() $\alpha \in {\mathfrak {d}}$
such that
$\alpha \in {\mathfrak {d}}$
such that
![]() $X\subseteq X_\alpha ^\beta $
, and consequently,
$X\subseteq X_\alpha ^\beta $
, and consequently,
![]() $X\cap T_\alpha ^\beta =\emptyset $
. Also we know that
$X\cap T_\alpha ^\beta =\emptyset $
. Also we know that
![]() $[A_\alpha ^\beta ]^\omega \subseteq [T_\alpha ^\beta ]$
, so
$[A_\alpha ^\beta ]^\omega \subseteq [T_\alpha ^\beta ]$
, so
![]() $X\cap ({\mathcal {B}}|A_\alpha ^\beta )=\emptyset $
. Indeed, if
$X\cap ({\mathcal {B}}|A_\alpha ^\beta )=\emptyset $
. Indeed, if
![]() $b\in X\cap ({\mathcal {B}}|A_\alpha ^\beta )$
, then there is
$b\in X\cap ({\mathcal {B}}|A_\alpha ^\beta )$
, then there is
![]() $Z\in [A_\alpha ^\beta ]^\omega $
such that
$Z\in [A_\alpha ^\beta ]^\omega $
such that
![]() $b\sqsubseteq Z$
, and, as
$b\sqsubseteq Z$
, and, as
![]() $Z\in [T_\alpha ^\beta ]$
, then
$Z\in [T_\alpha ^\beta ]$
, then
![]() $b\in T_\alpha ^\beta \cap X$
, which is a contradiction. This way, we have that
$b\in T_\alpha ^\beta \cap X$
, which is a contradiction. This way, we have that
![]() ${\mathcal {B}}|A_\alpha ^\beta \subseteq {\mathcal {B}}|R_\beta \subseteq S^i\cup X$
and
${\mathcal {B}}|A_\alpha ^\beta \subseteq {\mathcal {B}}|R_\beta \subseteq S^i\cup X$
and
![]() $({\mathcal {B}}|A_\alpha ^\beta )\cap X=\emptyset $
, so
$({\mathcal {B}}|A_\alpha ^\beta )\cap X=\emptyset $
, so
![]() ${\mathcal {B}}|A_\alpha ^\beta \subseteq S^i$
, and we are done.
${\mathcal {B}}|A_\alpha ^\beta \subseteq S^i$
, and we are done.
Question 6.14 Is
![]() ${\mathfrak {hom}}_{\mathcal {B}}={\mathfrak {hom}}_2$
for every nontrivial barrier
${\mathfrak {hom}}_{\mathcal {B}}={\mathfrak {hom}}_2$
for every nontrivial barrier
![]() ${\mathcal {B}}$
?
${\mathcal {B}}$
?
Acknowledgements
This research was done while the authors were part of the Thematic Program on Set Theoretic Methods in Algebra, Dynamics and Geometry at the Fields Institute. The authors thank the anonymous referee for their valuable suggestions, which improved the presentation of the paper – mainly, the end of Section 4 and the beginning of Section 5. We also thank the referee for pointing out the simpler proof for Corollary 6.5 presented here.