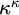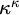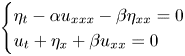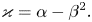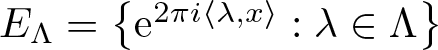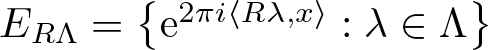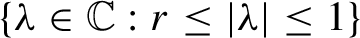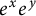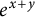76 results
GENERALIZED TOWER SPECTRA
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 10 January 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On spectra of Hankel operators on the polydisc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 301-317
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 2 - The Classification of Mood Disorders and the Unipolar/Bipolar Dichotomy
-
-
- Book:
- Clinical Textbook of Mood Disorders
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 10-36
-
- Chapter
- Export citation
28 - Legal Personhood and AI
- from Part IV - Comparative Perspectives
-
-
- Book:
- The Cambridge Handbook of Private Law and Artificial Intelligence
- Published online:
- 21 March 2024
- Print publication:
- 28 March 2024, pp 618-635
-
- Chapter
- Export citation
On the linearized Whitham–Broer–Kaup system on bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-20
-
- Article
- Export citation
The spectral eigenmatrix problems of planar self-affine measures with four digits
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 897-918
-
- Article
- Export citation
4 - The Frequency Domain and Pitch
-
- Book:
- Physics Behind Music
- Published online:
- 24 May 2023
- Print publication:
- 06 April 2023, pp 45-66
-
- Chapter
- Export citation
11 - Time Series
-
- Book:
- Introduction to Environmental Data Science
- Published online:
- 23 March 2023
- Print publication:
- 23 March 2023, pp 372-417
-
- Chapter
- Export citation
Friedrichs extensions for Sturm–Liouville operators with complex coefficients and their spectra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 18 November 2022, pp. 1883-1905
- Print publication:
- December 2023
-
- Article
- Export citation
4 - Eigenvalues of the Fractional p-Laplacian
-
- Book:
- Fractional Sobolev Spaces and Inequalities
- Published online:
- 06 October 2022
- Print publication:
- 13 October 2022, pp 63-74
-
- Chapter
- Export citation
8 - Hydrogen Atom
-
- Book:
- Quantum Mechanics
- Published online:
- 11 February 2023
- Print publication:
- 15 September 2022, pp 250-274
-
- Chapter
- Export citation
Regional spectral ratios as potential neural markers to identify mild cognitive impairment related to Alzheimer’s disease
-
- Journal:
- Acta Neuropsychiatrica / Volume 35 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 118-122
-
- Article
- Export citation
On the spectrum of non-self-adjoint Dirac operators with quasi-periodic boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 26 May 2022, pp. 1099-1117
- Print publication:
- August 2023
-
- Article
- Export citation
Sur le spectre des opérateurs rigides
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 01 March 2022, pp. 1351-1362
- Print publication:
- April 2023
-
- Article
- Export citation
3.7.9 - Mechanism of Action and Activity of Commonly Used Antibiotics
- from Section 3.7 - Infection and Immunity
-
-
- Book:
- Intensive Care Medicine
- Published online:
- 27 July 2023
- Print publication:
- 01 December 2021, pp 273-277
-
- Chapter
- Export citation
Commutativity via spectra of exponentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 815-824
- Print publication:
- December 2022
-
- Article
- Export citation
Eigenoscillations in an angular domain and spectral properties of functional equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 06 May 2021, pp. 538-559
-
- Article
- Export citation
1 - ʿAlī: A Contested Legacy
-
- Book:
- Opposing the Imam
- Published online:
- 29 April 2021
- Print publication:
- 29 April 2021, pp 15-38
-
- Chapter
- Export citation

Analysis and Geometry on Graphs and Manifolds
-
- Published online:
- 14 August 2020
- Print publication:
- 20 August 2020
7 - Broadcasting
- from Part II - Media-Dependent Entertainment
-
- Book:
- Entertainment Industry Economics
- Published online:
- 26 June 2020
- Print publication:
- 23 July 2020, pp 328-371
-
- Chapter
- Export citation