Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-07T22:26:29.611Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur le spectre des opérateurs rigides

Part of: General theory of linear operators Topological dynamics

Published online by Cambridge University Press:  01 March 2022

PIERRE MAZET  and
ERIC SAIAS
PIERRE MAZET
Affiliation:
Independent Scholar (e-mail: [email protected])
ERIC SAIAS*
Affiliation:
Sorbonne Université, Laboratoire de Probabilités, Statistique et Modélisation (LPSM) 4, place Jussieu, 75252 Paris Cedex 05, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For any 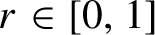$r\in [0,1]$ we give an example of a rigid operator whose spectrum is the annulus 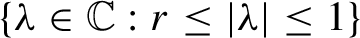$\{\lambda\in \mathbb{C} : r \le |\lambda| \le 1 \} $ . In particular, when 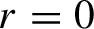$r=0$ this operator is rigid and non-invertible, and when 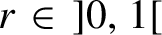$r\in {\kern1pt}] 0,1 [ $ this operator is invertible but its inverse is not rigid. This answers two questions of Costakis, Manoussos and Parissis [Recurrent linear operators. Complex Anal. Oper. Theory 8 (2014), 1601–1643].

Keywords

dynamical systemsrigid operatorsspectrum47A10

MSC classification

Primary: 37B20: Notions of recurrence 47A10: Spectrum, resolvent
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 4 , April 2023 , pp. 1351 - 1362
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Pour Mustapha Krazem, à l’occasion de son soixantiéme anniversaire

References

Bayart, F. and Matheron, E.. Dynamics of Linear Operators (Cambridge Tracts in Mathematics, 179).Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Costakis, G., Manoussos, A. and Parissis, I..Recurrent linear operators. Complex Anal. Oper. Theory 8 (2014),1601–1643.CrossRefGoogle Scholar
Grivaux, S. and Roginskaya, M.. On Read’s type operators on Hilbert spaces. Int. Math. Res.Not. IMRN 2008 (2008), rnn083.Google Scholar
Halmos, P.. A Hilbert Space Problem Book (Graduate Texts inMathematics, 19), 2nd edn. Springer-Verlag, New York,1982.CrossRefGoogle Scholar
Müller, V.. Local spectral radius formula for operators in Banachspaces. Czechoslovak Math. J. 38 (1988),726–729.CrossRefGoogle Scholar