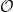 $\mathcal{O}$
$\mathcal{O}$
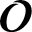 $\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS
$\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS
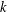 $k$TH YAU NUMBER OF ISOLATED HYPERSURFACE SINGULARITIES AND AN INEQUALITY CONJECTURE
$k$TH YAU NUMBER OF ISOLATED HYPERSURFACE SINGULARITIES AND AN INEQUALITY CONJECTURE