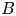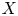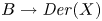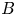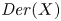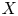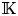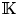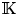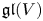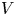Introduction
Groups act by automorphisms, and Lie algebras act by derivations: thus, via the semi-direct product construction, actions are equivalent to split extensions, while (up to isomorphism) any split extension of a group $B$![]() by a group $X$
by a group $X$![]() corresponds to a group homomorphism $B\to {\mathit {Aut}}(X)$
corresponds to a group homomorphism $B\to {\mathit {Aut}}(X)$![]() , and likewise for Lie algebras, with ${\mathit {Aut}}(X)$
, and likewise for Lie algebras, with ${\mathit {Aut}}(X)$![]() replaced by the Lie algebra ${\mathit {Der}}(X)$
replaced by the Lie algebra ${\mathit {Der}}(X)$![]() of derivations on $X$
of derivations on $X$![]() . In this article, we study the question whether the concept of a derivation can be extended from Lie algebras to other types of non-associative algebras, in such a way that these generalized derivations characterize the algebra actions.
. In this article, we study the question whether the concept of a derivation can be extended from Lie algebras to other types of non-associative algebras, in such a way that these generalized derivations characterize the algebra actions.
The situation sketched here has a categorical description due to F. Borceux, G. Janelidze and G. M. Kelly called action representability [Reference Borceux, Janelidze and Kelly3, Reference Borceux, Janelidze and Kelly4], which is expressed by saying that split extensions by an object $X$![]() are representable by an object $[X]$
are representable by an object $[X]$![]() . This means that we have a bijection ${\mathit {SpltExt}}(B,\,X) \cong {\mathit {Hom}}(B,\,[X])$
. This means that we have a bijection ${\mathit {SpltExt}}(B,\,X) \cong {\mathit {Hom}}(B,\,[X])$![]() , natural in $B$
, natural in $B$![]() , between the set of isomorphism classes of split extensions of $B$
, between the set of isomorphism classes of split extensions of $B$![]() by $X$
by $X$![]() and the set of morphisms from $B$
and the set of morphisms from $B$![]() to $[X]$
to $[X]$![]() . The object $[X]$
. The object $[X]$![]() corresponds to the group of automorphisms ${\mathit {Aut}}(X)$
corresponds to the group of automorphisms ${\mathit {Aut}}(X)$![]() in the case of groups or the algebra of derivations ${\mathit {Der}}(X)$
in the case of groups or the algebra of derivations ${\mathit {Der}}(X)$![]() in the case of Lie algebras. In [Reference Borceux, Janelidze and Kelly3, Reference Borceux, Janelidze and Kelly4], other examples such as Boolean rings are studied, as well as equivalent descriptions of the condition. A slightly different, more ‘object-wise’ approach appears in [Reference Casas, Datuashvili and Ladra7], where also an overview of the relevant literature is given.
in the case of Lie algebras. In [Reference Borceux, Janelidze and Kelly3, Reference Borceux, Janelidze and Kelly4], other examples such as Boolean rings are studied, as well as equivalent descriptions of the condition. A slightly different, more ‘object-wise’ approach appears in [Reference Casas, Datuashvili and Ladra7], where also an overview of the relevant literature is given.
In the present article, we work in the general setting of varieties of algebras over a field – ‘variety’ in the sense of universal algebra, which is different from its use in algebraic geometry. For a variety of non-associative algebras ${\mathcal {V}}$![]() over a field ${\mathbb {K}}$
over a field ${\mathbb {K}}$![]() , we seek an algebra $[X]$
, we seek an algebra $[X]$![]() in ${\mathcal {V}}$
in ${\mathcal {V}}$![]() that represents the split extensions of a given ${\mathcal {V}}$
that represents the split extensions of a given ${\mathcal {V}}$![]() -algebra $X$
-algebra $X$![]() . We show that such an algebra $[X]$
. We show that such an algebra $[X]$![]() cannot exist for each $X$
cannot exist for each $X$![]() in ${\mathcal {V}}$
in ${\mathcal {V}}$![]() , as soon as the field ${\mathbb {K}}$
, as soon as the field ${\mathbb {K}}$![]() is infinite, unless ${\mathcal {V}}$
is infinite, unless ${\mathcal {V}}$![]() is either ${\mathsf {Lie}}_{\mathbb {K}}$
is either ${\mathsf {Lie}}_{\mathbb {K}}$![]() , ${\mathsf {qLie}}_{\mathbb {K}}$
, ${\mathsf {qLie}}_{\mathbb {K}}$![]() , or an abelian category. We thus characterize the varieties of (quasi-)Lie algebras over an infinite field as the only varieties of non-associative algebras that form a non-abelian action representable category.
, or an abelian category. We thus characterize the varieties of (quasi-)Lie algebras over an infinite field as the only varieties of non-associative algebras that form a non-abelian action representable category.
Our method actually proves a significantly stronger result: it turns out that there is no loss in reducing the representability condition to abelian actions. These are usually called representations or Beck modules [Reference Beck2] and in the present context amount to actions on an abelian algebra – that is, an algebra whose multiplication is zero, so that the identity $xy=0$![]() holds; see below for a detailed explanation. We say that ${\mathcal {V}}$
holds; see below for a detailed explanation. We say that ${\mathcal {V}}$![]() has representable representations when for each abelian algebra $X$
has representable representations when for each abelian algebra $X$![]() , the contravariant functor ${\mathit {Rep}}(-,X)\colon {\mathcal {V}}\to {\mathsf {Set}}$
, the contravariant functor ${\mathit {Rep}}(-,X)\colon {\mathcal {V}}\to {\mathsf {Set}}$![]() that sends an algebra $B$
that sends an algebra $B$![]() to the set of $B$
to the set of $B$![]() -module structures on $X$
-module structures on $X$![]() is a representable functor, which means that it is naturally isomorphic to ${\mathit {Hom}}(-,[X])$
is a representable functor, which means that it is naturally isomorphic to ${\mathit {Hom}}(-,[X])$![]() for some ${\mathcal {V}}$
for some ${\mathcal {V}}$![]() -algebra $[X]$
-algebra $[X]$![]() . We show that, when it is a non-abelian category, such a variety ${\mathcal {V}}$
. We show that, when it is a non-abelian category, such a variety ${\mathcal {V}}$![]() is either ${\mathsf {Lie}}_{\mathbb {K}}$
is either ${\mathsf {Lie}}_{\mathbb {K}}$![]() or ${\mathsf {qLie}}_{\mathbb {K}}$
or ${\mathsf {qLie}}_{\mathbb {K}}$![]() , in which case $[X]$
, in which case $[X]$![]() is necessarily $\mathfrak {gl}(X)$
is necessarily $\mathfrak {gl}(X)$![]() , the Lie algebra of linear endomorphisms of the vector space $X$
, the Lie algebra of linear endomorphisms of the vector space $X$![]() . The object $\mathfrak {gl}(X)$
. The object $\mathfrak {gl}(X)$![]() is typical for (quasi-)Lie algebras, in the sense that no other non-abelian variety of ${\mathbb {K}}$
is typical for (quasi-)Lie algebras, in the sense that no other non-abelian variety of ${\mathbb {K}}$![]() -algebras has an object $[X]$
-algebras has an object $[X]$![]() representing the module structures on $X$
representing the module structures on $X$![]() . In other words, changing the variety breaks $\mathfrak {gl}(X)$
. In other words, changing the variety breaks $\mathfrak {gl}(X)$![]() beyond repair.
beyond repair.
Overview of the text
The article is organized as follows. In § 1, we recall some basic definitions and results concerning varieties of non-associative algebras. We introduce actions and the condition that they are representable in the context of semi-abelian categories. We explain what this amounts to in varieties of non-associative algebras. Then, we discuss the concept of a representation.
In § 2, we prove that for a variety, representability of its representations implies a condition called algebraic coherence. This allows us to work with the $\lambda / \mu$![]() -rules, which are identities of degree three, useful in what follows. In § 3, the idea is to show that some identities of degree two – necessarily commutativity or anti-commutativity – follow from representability of representations. In order to get these results, we use two computer programs, which probably makes § 3 the most innovative section of this paper. In § 4, the goal is to observe that only anti-commutativity is consistent with representability of representations, as long as the variety is non-abelian. From this, we deduce that the $\lambda / \mu$
-rules, which are identities of degree three, useful in what follows. In § 3, the idea is to show that some identities of degree two – necessarily commutativity or anti-commutativity – follow from representability of representations. In order to get these results, we use two computer programs, which probably makes § 3 the most innovative section of this paper. In § 4, the goal is to observe that only anti-commutativity is consistent with representability of representations, as long as the variety is non-abelian. From this, we deduce that the $\lambda / \mu$![]() -rules can be reduced to the Jacobi identity. In § 5, we answer a final question which arises naturally from the previous sections. A priori, anti-commutativity and the Jacobi identity need not be the only identities satisfied in a variety with representable representations. We prove that there is indeed nothing else.
-rules can be reduced to the Jacobi identity. In § 5, we answer a final question which arises naturally from the previous sections. A priori, anti-commutativity and the Jacobi identity need not be the only identities satisfied in a variety with representable representations. We prove that there is indeed nothing else.
In § 6, we conclude with Theorem 6.1, the goal and main result of this paper. We position our work within the context of similar results in the literature and discuss some open problems.
1 Preliminaries
1.1 Varieties of algebras
An algebra $A$![]() on a field ${\mathbb {K}}$
on a field ${\mathbb {K}}$![]() is a ${\mathbb {K}}$
is a ${\mathbb {K}}$![]() -vector space equipped with a bilinear map ${A \times A\rightarrow A\colon (x,\,y)\mapsto xy=x\cdot y=[x,\,y]}$
-vector space equipped with a bilinear map ${A \times A\rightarrow A\colon (x,\,y)\mapsto xy=x\cdot y=[x,\,y]}$![]() called the multiplication or bracket. A morphism of algebras is therefore a ${\mathbb {K}}$
called the multiplication or bracket. A morphism of algebras is therefore a ${\mathbb {K}}$![]() -linear map $f\colon A \rightarrow B$
-linear map $f\colon A \rightarrow B$![]() which preserves this multiplication. This determines the category ${\mathsf {Alg}}_{\mathbb {K}}$
which preserves this multiplication. This determines the category ${\mathsf {Alg}}_{\mathbb {K}}$![]() of algebras over ${\mathbb {K}}$
of algebras over ${\mathbb {K}}$![]() . We remark that for now we do not require the multiplication to be associative.
. We remark that for now we do not require the multiplication to be associative.
We call a collection of ${\mathbb {K}}$![]() -algebras a variety of (non-associative) algebras over ${\mathbb {K}}$
-algebras a variety of (non-associative) algebras over ${\mathbb {K}}$![]() if the collection contains all the algebras satisfying a chosen set of polynomial equations. For example, the variety ${\mathsf {Lie}}_{{\mathbb {K}}}$
if the collection contains all the algebras satisfying a chosen set of polynomial equations. For example, the variety ${\mathsf {Lie}}_{{\mathbb {K}}}$![]() of Lie algebras corresponds to the collection of all algebras over ${\mathbb {K}}$
of Lie algebras corresponds to the collection of all algebras over ${\mathbb {K}}$![]() satisfying the Jacobi identity ($x(yz)+ y(zx) + z(xy)=0$
satisfying the Jacobi identity ($x(yz)+ y(zx) + z(xy)=0$![]() ) and alternativity ($xx=0$
) and alternativity ($xx=0$![]() ), while ${\mathsf {qLie}}_{{\mathbb {K}}}$
), while ${\mathsf {qLie}}_{{\mathbb {K}}}$![]() denotes the variety of quasi-Lie algebras where alternativity is replaced by anticommutativity ($xy+ yx =0$
denotes the variety of quasi-Lie algebras where alternativity is replaced by anticommutativity ($xy+ yx =0$![]() ). Of course when ${\mathit {char}}({\mathbb {K}}) \neq 2$
). Of course when ${\mathit {char}}({\mathbb {K}}) \neq 2$![]() , quasi-Lie algebras and Lie algebras are the same. However, for characteristic $2$
, quasi-Lie algebras and Lie algebras are the same. However, for characteristic $2$![]() , alternativity implies anticommutativity but the converse is not true. In this case, the variety of Lie algebras is strictly smaller than the variety of quasi-Lie algebras.
, alternativity implies anticommutativity but the converse is not true. In this case, the variety of Lie algebras is strictly smaller than the variety of quasi-Lie algebras.
We say that an algebra is abelian if $xy=0$![]() holds for every $x$
holds for every $x$![]() and $y$
and $y$![]() in the algebra. The variety of abelian ${\mathbb {K}}$
in the algebra. The variety of abelian ${\mathbb {K}}$![]() -algebras is trivially equivalent to the (abelian) category ${\mathsf {Vect}}_{{\mathbb {K}}}$
-algebras is trivially equivalent to the (abelian) category ${\mathsf {Vect}}_{{\mathbb {K}}}$![]() of vectors spaces over ${\mathbb {K}}$
of vectors spaces over ${\mathbb {K}}$![]() . Each variety of ${\mathbb {K}}$
. Each variety of ${\mathbb {K}}$![]() -algebras contains all abelian algebras over ${\mathbb {K}}$
-algebras contains all abelian algebras over ${\mathbb {K}}$![]() , and these are precisely those algebras that admit an internal abelian group structure in the category ${\mathcal {V}}$
, and these are precisely those algebras that admit an internal abelian group structure in the category ${\mathcal {V}}$![]() .
.
Remark 1.2 Any variety ${\mathcal {V}}$![]() of non-associative algebras is a Janelidze–Márki–Tholen semi-abelian category [Reference Janelidze, Márki and Tholen22]. Indeed, any variety of algebras is in particular a variety of $\Omega$
of non-associative algebras is a Janelidze–Márki–Tholen semi-abelian category [Reference Janelidze, Márki and Tholen22]. Indeed, any variety of algebras is in particular a variety of $\Omega$![]() -groups in the sense of Higgins [Reference Higgins21].
-groups in the sense of Higgins [Reference Higgins21].
We recall some additional concepts in order to cite two theorems we shall need later on. Let $F\colon {\mathsf {Set}} \rightarrow {\mathsf {Alg}}_{\mathbb {K}}$![]() be the free algebra functor sending a set $S$
be the free algebra functor sending a set $S$![]() to the free algebra over ${\mathbb {K}}$
to the free algebra over ${\mathbb {K}}$![]() generated by the elements of $S$
generated by the elements of $S$![]() . We recall that it is a left adjoint functor (its right adjoint being the forgetful functor) which factorizes through the free magma functor $M\colon {\mathsf {Set}} \rightarrow {\mathsf {Mag}}$
. We recall that it is a left adjoint functor (its right adjoint being the forgetful functor) which factorizes through the free magma functor $M\colon {\mathsf {Set}} \rightarrow {\mathsf {Mag}}$![]() (sending $S$
(sending $S$![]() to the magma $M(S)$
to the magma $M(S)$![]() of non-empty words in $S$
of non-empty words in $S$![]() ) and the magma algebra functor ${\mathbb {K}}[-]\colon {{\mathsf {Mag}} \rightarrow {\mathsf {Alg}}_{\mathbb {K}}}$
) and the magma algebra functor ${\mathbb {K}}[-]\colon {{\mathsf {Mag}} \rightarrow {\mathsf {Alg}}_{\mathbb {K}}}$![]() . A (non-associative) polynomial $\varphi$
. A (non-associative) polynomial $\varphi$![]() on a set $S$
on a set $S$![]() is an element of ${\mathbb {K}}[M(S)]$
is an element of ${\mathbb {K}}[M(S)]$![]() . We say that $\varphi$
. We say that $\varphi$![]() is a monomial if it is a scalar multiple of an element of $M(S)$
is a monomial if it is a scalar multiple of an element of $M(S)$![]() . The type of a monomial $\varphi = \varphi (x_1,\, \ldots ,\, x_n)$
. The type of a monomial $\varphi = \varphi (x_1,\, \ldots ,\, x_n)$![]() is a $n$
is a $n$![]() -tuple $(k_1,\, \ldots ,\, k_n)\in {\mathbb {N}}^{n}$
-tuple $(k_1,\, \ldots ,\, k_n)\in {\mathbb {N}}^{n}$![]() where $k_i$
where $k_i$![]() is the number of times $x_i$
is the number of times $x_i$![]() appears in $\varphi$
appears in $\varphi$![]() . Its degree is the number $k_1+\cdots +k_n$
. Its degree is the number $k_1+\cdots +k_n$![]() . A polynomial is said to be homogeneous if all its monomials are of the same type. We can decompose every polynomial into its homogeneous components.
. A polynomial is said to be homogeneous if all its monomials are of the same type. We can decompose every polynomial into its homogeneous components.
Proposition 1.3 If ${\mathcal {V}}$![]() is a variety of non-associative ${\mathbb {K}}$
is a variety of non-associative ${\mathbb {K}}$![]() -algebras satisfying a non-trivial homogeneous identity of degree $2$
-algebras satisfying a non-trivial homogeneous identity of degree $2$![]() , then ${\mathcal {V}}$
, then ${\mathcal {V}}$![]() is either a subvariety of the variety of commutative algebras, or a subvariety of the variety of anticommutative algebras.
is either a subvariety of the variety of commutative algebras, or a subvariety of the variety of anticommutative algebras.
Proof. We want to prove that essentially the only two possibilities are commutativity $(xy=yx)$![]() and anticommutativity $(xy=-yx)$
and anticommutativity $(xy=-yx)$![]() . In fact, alternativity is also a non-trivial identity. But since $xx=0$
. In fact, alternativity is also a non-trivial identity. But since $xx=0$![]() implies anticommutativity, we can assume $\varphi$
implies anticommutativity, we can assume $\varphi$![]() to be $xy + \lambda yx =0$
to be $xy + \lambda yx =0$![]() for some $\lambda \in {\mathbb {K}}$
for some $\lambda \in {\mathbb {K}}$![]() without any loss of generality. This implies that $xy= -\lambda yx$
without any loss of generality. This implies that $xy= -\lambda yx$![]() and thus $(1-\lambda ^{2} )xy=0$
and thus $(1-\lambda ^{2} )xy=0$![]() . Therefore, either ${\mathcal {V}}$
. Therefore, either ${\mathcal {V}}$![]() is an abelian variety, or $\lambda =\pm 1$
is an abelian variety, or $\lambda =\pm 1$![]() , which proves the result.
, which proves the result.
Theorem 1.4 (Bahturin [Reference Bahturin1] and Zhevlakov et al [Reference Zhevlakov, Slin'ko, Shestakov and Shirshov29])
If ${\mathcal {V}}$![]() is a variety of algebras over an infinite field, then all of its identities are of the form $\phi (x_{1},\,\ldots ,\,x_{n})=0$
is a variety of algebras over an infinite field, then all of its identities are of the form $\phi (x_{1},\,\ldots ,\,x_{n})=0$![]() , where $\phi (x_{1},\,\ldots ,\,x_{n})$
, where $\phi (x_{1},\,\ldots ,\,x_{n})$![]() is a polynomial, each of whose homogeneous components $\psi (x_{i_{1}},\,\ldots ,\, x_{i_{m}})$
is a polynomial, each of whose homogeneous components $\psi (x_{i_{1}},\,\ldots ,\, x_{i_{m}})$![]() again gives rise to an identity $\psi (x_{i_{1}},\,\ldots ,\, x_{i_{m}})=0$
again gives rise to an identity $\psi (x_{i_{1}},\,\ldots ,\, x_{i_{m}})=0$![]() in ${\mathcal {V}}$
in ${\mathcal {V}}$![]() .
.
Unless we specify it otherwise, we shall always assume that ${\mathbb {K}}$![]() is an infinite field, so that we can use the previous result. For instance, when ${\mathcal {V}}$
is an infinite field, so that we can use the previous result. For instance, when ${\mathcal {V}}$![]() is a variety of ${\mathbb {K}}$
is a variety of ${\mathbb {K}}$![]() -algebras that satisfies a non-trivial identity involving monomials of degree $2$
-algebras that satisfies a non-trivial identity involving monomials of degree $2$![]() , then Proposition 1.3 applies and tells us that ${\mathcal {V}}$
, then Proposition 1.3 applies and tells us that ${\mathcal {V}}$![]() consists of either commutative or anticommutative algebras.
consists of either commutative or anticommutative algebras.
A homogeneous polynomial is multilinear if its monomials are of the type $(1,\, 1,\, \ldots ,\, 1)$![]() . A multilinear identity is therefore an identity $\varphi (x_1,\,\ldots ,\,x_n)=0$
. A multilinear identity is therefore an identity $\varphi (x_1,\,\ldots ,\,x_n)=0$![]() where $\varphi$
where $\varphi$![]() is a multilinear polynomial.
is a multilinear polynomial.
Theorem 1.5 (Theorem 3 in § 4.2 of [Reference Bahturin1])
In a subvariety of ${\mathsf {Lie}}_{{\mathbb {K}}}$![]() , any non-trivial identity has a non-trivial multilinear consequence.
, any non-trivial identity has a non-trivial multilinear consequence.
1.6 Actions of algebras
Let ${\mathcal {V}}$![]() be a semi-abelian category [Reference Janelidze, Márki and Tholen22] and $B$
be a semi-abelian category [Reference Janelidze, Márki and Tholen22] and $B$![]() be an object in
be an object in ![]() ${\mathcal {V}}$. We write ${\mathsf {Pt}}_B({\mathcal {V}})$
${\mathcal {V}}$. We write ${\mathsf {Pt}}_B({\mathcal {V}})$![]() for the category of points over $B$
for the category of points over $B$![]() whose objects are triples $(A,\,p,\,s)$
whose objects are triples $(A,\,p,\,s)$![]() where $A$
where $A$![]() is an object in ${\mathcal {V}}$
is an object in ${\mathcal {V}}$![]() and $p\colon A\rightarrow B$
and $p\colon A\rightarrow B$![]() is a split epimorphism with a given section $s$
is a split epimorphism with a given section $s$![]() . It is well known [Reference Bourn and Janelidze5] that the functor $K\colon {\mathsf {Pt}}_B({\mathcal {V}}) \rightarrow {\mathcal {V}}$
. It is well known [Reference Bourn and Janelidze5] that the functor $K\colon {\mathsf {Pt}}_B({\mathcal {V}}) \rightarrow {\mathcal {V}}$![]() sending a point $(A,\,p,\,s)$
sending a point $(A,\,p,\,s)$![]() over $B$
over $B$![]() to the kernel of $p$
to the kernel of $p$![]() is monadic. The corresponding monad on ${\mathcal {V}}$
is monadic. The corresponding monad on ${\mathcal {V}}$![]() is the functor $B \flat (-)\colon {\mathcal {V}} \to {\mathcal {V}}\colon X \mapsto B\flat X$
is the functor $B \flat (-)\colon {\mathcal {V}} \to {\mathcal {V}}\colon X \mapsto B\flat X$![]() where the object $B\flat X$
where the object $B\flat X$![]() is the kernel of $(1_B,\,0)\colon B + X \to B$
is the kernel of $(1_B,\,0)\colon B + X \to B$![]() , together with certain natural transformations $\eta ^{B}\colon 1_{{\mathcal {V}}}\Rightarrow B \flat (-)$
, together with certain natural transformations $\eta ^{B}\colon 1_{{\mathcal {V}}}\Rightarrow B \flat (-)$![]() and $\mu ^{B}\colon B \flat (B \flat (-))\Rightarrow B \flat (-)$
and $\mu ^{B}\colon B \flat (B \flat (-))\Rightarrow B \flat (-)$![]() . Here $\mu ^{B}_X$
. Here $\mu ^{B}_X$![]() is a restriction of the codiagonal $(B+B)+X\to B+X$
is a restriction of the codiagonal $(B+B)+X\to B+X$![]() and $\eta ^{B}_X$
and $\eta ^{B}_X$![]() sends an element of $X$
sends an element of $X$![]() to itself, considered as an element of $B\flat X$
to itself, considered as an element of $B\flat X$![]() . A $B \flat (-)$
. A $B \flat (-)$![]() -algebra $(X,\,\xi )$
-algebra $(X,\,\xi )$![]() is an object $X$
is an object $X$![]() together with a morphism $\xi \colon B \flat X \rightarrow X$
together with a morphism $\xi \colon B \flat X \rightarrow X$![]() called an action of $B$
called an action of $B$![]() on $X$
on $X$![]() , such that the diagrams
, such that the diagrams

commute. We write ${\mathit {Act}}(B,\,X)$![]() for the set of actions of $B$
for the set of actions of $B$![]() on $X$
on $X$![]() . One equivalent way of viewing actions uses split extensions:
. One equivalent way of viewing actions uses split extensions:
Lemma 1.7 (Borceux [Reference Borceux, Janelidze and Kelly4] and Bourn & Janelidze [Reference Bourn and Janelidze5])
Given objects $B$![]() and $X$
and $X$![]() in a semi-abelian category, there is a bijection ${\mathit {SpltExt}}(B,\,X) \cong {\mathit {Act}}(B,\,X)$
in a semi-abelian category, there is a bijection ${\mathit {SpltExt}}(B,\,X) \cong {\mathit {Act}}(B,\,X)$![]() between the set of isomorphism classes of split extensions of $B$
between the set of isomorphism classes of split extensions of $B$![]() by $X$
by $X$![]() and the set of actions of $B$
and the set of actions of $B$![]() on $X$
on $X$![]() .
.
In fact, for any action $\xi \colon B \flat X \rightarrow X$![]() there is a split extension of $B$
there is a split extension of $B$![]() by $X$
by $X$![]()
and vice versa. The object $H$![]() in this split extension is called the semi-direct product of $B$
in this split extension is called the semi-direct product of $B$![]() with $(X,\,\xi )$
with $(X,\,\xi )$![]() , written $B \ltimes _\xi X$
, written $B \ltimes _\xi X$![]() . In a variety of non-associative algebras, what is its structure?
. In a variety of non-associative algebras, what is its structure?
First, since it is the kernel of the morphism $(1_B,\,0)\colon {B+X\to B}$![]() , the object ${B \flat X}$
, the object ${B \flat X}$![]() consists of polynomials with variables in $B$
consists of polynomials with variables in $B$![]() and $X$
and $X$![]() which can be written in a form where all of their monomials contain variables in $X$
which can be written in a form where all of their monomials contain variables in $X$![]() .
.
Then, by applying the forgetful functor $U\colon {\mathcal {V}} \rightarrow {\mathsf {Vect}}$![]() , we observe that, as a vector space, $B \ltimes _\xi X$
, we observe that, as a vector space, $B \ltimes _\xi X$![]() is the direct sum/Cartesian product $B \oplus X\cong B\times X$
is the direct sum/Cartesian product $B \oplus X\cong B\times X$![]() . Next, routine calculations show us that the multiplication has to be
. Next, routine calculations show us that the multiplication has to be
where $^{b}y$![]() and $x^{c}$
and $x^{c}$![]() are notation for the image by $\xi$
are notation for the image by $\xi$![]() in $X$
in $X$![]() of $by$
of $by$![]() and $xc$
and $xc$![]() , respectively. Sometimes, for the sake of simplicity, we will just write $by$
, respectively. Sometimes, for the sake of simplicity, we will just write $by$![]() or $xc$
or $xc$![]() . We remark that starting with a morphism $\xi \colon B \flat X \rightarrow X$
. We remark that starting with a morphism $\xi \colon B \flat X \rightarrow X$![]() (not necessary an action) we can still define a semi-direct product ${\mathbb {K}}$
(not necessary an action) we can still define a semi-direct product ${\mathbb {K}}$![]() -algebra by (*). The question is now, whether this algebra belongs to the variety ${\mathcal {V}}$
-algebra by (*). The question is now, whether this algebra belongs to the variety ${\mathcal {V}}$![]() .
.
Lemma 1.8 Let ${\mathcal {V}}$![]() be a variety of non-associative algebras over a field ${\mathbb {K}}$
be a variety of non-associative algebras over a field ${\mathbb {K}}$![]() , let $B$
, let $B$![]() and $X$
and $X$![]() be two algebras and $\xi \colon B \flat X \rightarrow X$
be two algebras and $\xi \colon B \flat X \rightarrow X$![]() a morphism in ${\mathcal {V}}$
a morphism in ${\mathcal {V}}$![]() such that $\xi\circ\eta^B_X=1_X$
such that $\xi\circ\eta^B_X=1_X$![]() . Then $\xi$
. Then $\xi$![]() is an action in ${\mathcal {V}}$
is an action in ${\mathcal {V}}$![]() if and only if $B \ltimes _\xi X$
if and only if $B \ltimes _\xi X$![]() is in ${\mathcal {V}}$
is in ${\mathcal {V}}$![]() .
.
Proof. The first implication directly comes from the equivalence in Lemma 1.6. For the converse, we construct the split extension
in ${\mathcal {V}}$![]() , where $k(x)=(0,\,x)$
, where $k(x)=(0,\,x)$![]() , $p(b,\,x)=b$
, $p(b,\,x)=b$![]() and $s(b)=(b,\,0)$
and $s(b)=(b,\,0)$![]() . Lemma 1.6 then gives us an action $\chi \colon B \flat X \rightarrow X$
. Lemma 1.6 then gives us an action $\chi \colon B \flat X \rightarrow X$![]() in ${\mathcal {V}}$
in ${\mathcal {V}}$![]() which is, by construction, the only morphism satisfying $k {\scriptstyle {\circ }} \chi = (s,\,k) {\scriptstyle {\circ }} l$
which is, by construction, the only morphism satisfying $k {\scriptstyle {\circ }} \chi = (s,\,k) {\scriptstyle {\circ }} l$![]() where $l$
where $l$![]() is the kernel of $(1_B,\,0)\colon B + X \to B$
is the kernel of $(1_B,\,0)\colon B + X \to B$![]() . But $\xi$
. But $\xi$![]() obviously satisfies this condition and therefore coincides with $\chi$
obviously satisfies this condition and therefore coincides with $\chi$![]() .
.
This description of actions, analogous to Theorem 2.5 of [Reference Casas, Datuashvili and Ladra7], will be useful all along this paper, whenever we wish to check that an action is well defined. For example, let ${\mathcal {V}}$![]() be the variety of commutative algebras over an arbitrary field ${\mathbb {K}}$
be the variety of commutative algebras over an arbitrary field ${\mathbb {K}}$![]() , and let $V$
, and let $V$![]() be an algebra in this variety. Then $V$
be an algebra in this variety. Then $V$![]() acts on itself by $^{v}w=v\cdot w$
acts on itself by $^{v}w=v\cdot w$![]() and $v^{w}=v\cdot w$
and $v^{w}=v\cdot w$![]() . Indeed, the semi-direct product ${\mathbb {K}}$
. Indeed, the semi-direct product ${\mathbb {K}}$![]() -algebra is in ${\mathcal {V}}$
-algebra is in ${\mathcal {V}}$![]() , since for all $v$
, since for all $v$![]() , $v'$
, $v'$![]() , $w$
, $w$![]() , $w'\in V$
, $w'\in V$![]() we have $(v,\,w)\cdot (v',\,w') =(v',\,w')\cdot (v,\,w)$
we have $(v,\,w)\cdot (v',\,w') =(v',\,w')\cdot (v,\,w)$![]() .
.
1.9 Action representability
Let ${\mathcal {V}}$![]() be a semi-abelian category. For a fixed object $X$
be a semi-abelian category. For a fixed object $X$![]() in the category, ${{\mathit {Act}}(-,X)\colon {\mathcal {V}} \rightarrow {\mathsf {Set}}}$
in the category, ${{\mathit {Act}}(-,X)\colon {\mathcal {V}} \rightarrow {\mathsf {Set}}}$![]() defines a contravariant functor sending an object $B\in {\mathcal {V}}$
defines a contravariant functor sending an object $B\in {\mathcal {V}}$![]() to the set of actions of $B$
to the set of actions of $B$![]() on $X$
on $X$![]() . We say that the category ${\mathcal {V}}$
. We say that the category ${\mathcal {V}}$![]() is action representable when for each object $X$
is action representable when for each object $X$![]() in ${\mathcal {V}}$
in ${\mathcal {V}}$![]() the functor ${\mathit {Act}}(-,X)$
the functor ${\mathit {Act}}(-,X)$![]() is representable [Reference Borceux, Janelidze and Kelly4]. This means that there exists an object $[ X]$
is representable [Reference Borceux, Janelidze and Kelly4]. This means that there exists an object $[ X]$![]() , called the actor of $X$
, called the actor of $X$![]() , in ${\mathcal {V}}$
, in ${\mathcal {V}}$![]() and a natural isomorphism
and a natural isomorphism
An interesting question is the role of the actor in concrete examples: What is then its structure? In ${\mathsf {Grp}}$![]() , the actor of an object $X$
, the actor of an object $X$![]() is the automorphism group ${\mathit {Aut}}(X)$
is the automorphism group ${\mathit {Aut}}(X)$![]() ; in ${\mathsf {Lie}}_{\mathbb {K}}$
; in ${\mathsf {Lie}}_{\mathbb {K}}$![]() , the actor of $X$
, the actor of $X$![]() is the Lie algebra of its derivations ${\mathit {Der}}(X)$
is the Lie algebra of its derivations ${\mathit {Der}}(X)$![]() . More examples are studied in [Reference Borceux, Janelidze and Kelly4], and new examples continue to be studied, as for crossed modules (in [Reference Ramasu28]) and for cocommutative Hopf algebras (in [Reference Gran, Kadjo and Vercruysse17]).
. More examples are studied in [Reference Borceux, Janelidze and Kelly4], and new examples continue to be studied, as for crossed modules (in [Reference Ramasu28]) and for cocommutative Hopf algebras (in [Reference Gran, Kadjo and Vercruysse17]).
Proposition 1.10 Let ${\mathcal {V}}$![]() be a variety of non-associative algebras over ${\mathbb {K}}$
be a variety of non-associative algebras over ${\mathbb {K}}$![]() . Then ${\mathcal {V}}$
. Then ${\mathcal {V}}$![]() is action representable if and only if for every object $X$
is action representable if and only if for every object $X$![]() in ${\mathcal {V}}$
in ${\mathcal {V}}$![]() there exists an object $[X]$
there exists an object $[X]$![]() acting on $X$
acting on $X$![]() which has the following property: for any object $B$
which has the following property: for any object $B$![]() with an action on $X$
with an action on $X$![]() there is a unique morphism $\varphi \colon B \rightarrow [X]$
there is a unique morphism $\varphi \colon B \rightarrow [X]$![]() such that $^{b}x= {}^{\varphi (b)}x$
such that $^{b}x= {}^{\varphi (b)}x$![]() and $x^{b}=x^{\varphi (b)}$
and $x^{b}=x^{\varphi (b)}$![]() for every $x\in X$
for every $x\in X$![]() and $b\in B$
and $b\in B$![]() .
.
Proof. This is a reformulation of Proposition 3.1 from [Reference Casas, Datuashvili and Ladra7] for the context of varieties of non-associative algebras, which are all categories of groups with operations in the sense of [Reference Porter27].
In [Reference Borceux, Janelidze and Kelly4], it is explained that action representability in so-called locally well-presentable semi-abelian categories is equivalent to the condition that ${\mathit {Act}}(-,\,X)$![]() preserves binary coproducts for every object $X$
preserves binary coproducts for every object $X$![]() . Actually, the isomorphism ${\mathit {Act}}(-,X) \cong {\mathit {Hom}}(-,[X])$
. Actually, the isomorphism ${\mathit {Act}}(-,X) \cong {\mathit {Hom}}(-,[X])$![]() easily implies that ${\mathit {Act}}(B + B',\,X) \cong {\mathit {Act}}(B,\,X) \times {\mathit {Act}}(B',\,X)$
easily implies that ${\mathit {Act}}(B + B',\,X) \cong {\mathit {Act}}(B,\,X) \times {\mathit {Act}}(B',\,X)$![]() , which can be understood as the condition that ‘having an action of $B+B'$
, which can be understood as the condition that ‘having an action of $B+B'$![]() on $X$
on $X$![]() is the same as having two actions on $X$
is the same as having two actions on $X$![]() , one of $B$
, one of $B$![]() and the other of $B'$
and the other of $B'$![]() .’
.’
From this observation, we may now deduce an interesting and useful technique. Indeed, by Lemma 1.7, the object $(B+B') \ltimes X$![]() is in ${\mathcal {V}}$
is in ${\mathcal {V}}$![]() and as such should satisfy the identities characterizing ${\mathcal {V}}$
and as such should satisfy the identities characterizing ${\mathcal {V}}$![]() , whenever the variety is action representable. We remark that this stays true with a finite number of algebras acting on $X$
, whenever the variety is action representable. We remark that this stays true with a finite number of algebras acting on $X$![]() . Checking this condition is an important proof method used throughout this article. Let us give a concrete example of how this works, by reproving the known result that in the variety of associative algebras, the actor cannot always exist:
. Checking this condition is an important proof method used throughout this article. Let us give a concrete example of how this works, by reproving the known result that in the variety of associative algebras, the actor cannot always exist:
Proposition 1.11 Let ${\mathbb {K}}$![]() be a field, and ${\mathsf {AAlg}_{\mathbb {K}}}$
be a field, and ${\mathsf {AAlg}_{\mathbb {K}}}$![]() the variety of associative algebras over ${\mathbb {K}}$
the variety of associative algebras over ${\mathbb {K}}$![]() (defined by $(xy)z=x(yz)$
(defined by $(xy)z=x(yz)$![]() ). Then ${\mathsf {AAlg}_{\mathbb {K}}}$
). Then ${\mathsf {AAlg}_{\mathbb {K}}}$![]() is not action representable.
is not action representable.
Proof. Suppose that ${\mathsf {AAlg}_{\mathbb {K}}}$![]() is action representable. Let $B^{1}$
is action representable. Let $B^{1}$![]() and $B^{2}$
and $B^{2}$![]() be two algebras with trivial multiplication respectively generated by the elements $b^{1}$
be two algebras with trivial multiplication respectively generated by the elements $b^{1}$![]() and $b^{2}$
and $b^{2}$![]() . Let $X$
. Let $X$![]() be the algebra with trivial multiplication generated by the elements $x$
be the algebra with trivial multiplication generated by the elements $x$![]() , $y^{1}$
, $y^{1}$![]() , $y^{2}$
, $y^{2}$![]() , $z^{12}$
, $z^{12}$![]() and $z^{21}$
and $z^{21}$![]() . Those algebras are in ${\mathsf {AAlg}_{\mathbb {K}}}$
. Those algebras are in ${\mathsf {AAlg}_{\mathbb {K}}}$![]() . We define the actions of $B^{i}$
. We define the actions of $B^{i}$![]() on $X$
on $X$![]() by:
by:

where $i$![]() , $j$
, $j$![]() , $k\in \{1,\,2\}$
, $k\in \{1,\,2\}$![]() and $j\neq k$
and $j\neq k$![]() . These choices determine morphisms of ${\mathcal {V}}$
. These choices determine morphisms of ${\mathcal {V}}$![]() -algebras $\xi ^{i}\colon B^{i}\flat X\to X$
-algebras $\xi ^{i}\colon B^{i}\flat X\to X$![]() , and Lemma 1.8 implies that those are well-defined actions. Since we supposed ${\mathsf {AAlg}_{\mathbb {K}}}$
, and Lemma 1.8 implies that those are well-defined actions. Since we supposed ${\mathsf {AAlg}_{\mathbb {K}}}$![]() action representable, also the algebra $B^{1} + B^{2}$
action representable, also the algebra $B^{1} + B^{2}$![]() acts on $X$
acts on $X$![]() . Yet $(B^{1}+B^{2})\ltimes X$
. Yet $(B^{1}+B^{2})\ltimes X$![]() is not in ${\mathsf {AAlg}_{\mathbb {K}}}$
is not in ${\mathsf {AAlg}_{\mathbb {K}}}$![]() , which is a contradiction. Indeed, we have that $b^{1}(xb^{2})=z^{12} \neq z^{21} = (b^{1}x) b^{2}$
, which is a contradiction. Indeed, we have that $b^{1}(xb^{2})=z^{12} \neq z^{21} = (b^{1}x) b^{2}$![]() .
.
Theorem 1.12 ${\mathsf {Lie}}_{\mathbb {K}}$![]() and ${\mathsf {qLie}}_{\mathbb {K}}$
and ${\mathsf {qLie}}_{\mathbb {K}}$![]() are action representable for any field ${\mathbb {K}}$
are action representable for any field ${\mathbb {K}}$![]() .
.
Proof. For Lie algebras, this is a well-known result proved in [Reference Borceux, Janelidze and Kelly3, Reference Borceux, Janelidze and Kelly4]. The case of quasi-Lie algebras, for a field of characteristic $2$![]() , is not explicit there, but the essence of the proof stays valid. In any case, the actor of an object $X$
, is not explicit there, but the essence of the proof stays valid. In any case, the actor of an object $X$![]() in one of those categories is the algebra of derivations ${\mathit {Der}}(X)$
in one of those categories is the algebra of derivations ${\mathit {Der}}(X)$![]() .
.
1.13 Representations and their representability
Given an object $B$![]() in ${\mathcal {V}}$
in ${\mathcal {V}}$![]() , a Beck module [Reference Beck2] over $B$
, a Beck module [Reference Beck2] over $B$![]() , also called a $B$
, also called a $B$![]() -module or a representation of $B$
-module or a representation of $B$![]() , is an abelian group object in the slice category $({\mathcal {V}}\downarrow B)$
, is an abelian group object in the slice category $({\mathcal {V}}\downarrow B)$![]() . As is well known (and explained in detail for instance in [Reference Hartl and Van der Linden20]), in a semi-abelian category that satisfies the so-called Smith is Huq condition, a $B$
. As is well known (and explained in detail for instance in [Reference Hartl and Van der Linden20]), in a semi-abelian category that satisfies the so-called Smith is Huq condition, a $B$![]() -module structure on a (necessarily abelian) object $X$
-module structure on a (necessarily abelian) object $X$![]() of ${\mathcal {V}}$
of ${\mathcal {V}}$![]() is the same thing as a $B$
is the same thing as a $B$![]() -action on $X$
-action on $X$![]() – an ‘abelian action’. Combining the results of [Reference Mantovani and Metere23, Reference Martins-Ferreira and Van der Linden24] with the fact that any variety of non-associative ${\mathbb {K}}$
– an ‘abelian action’. Combining the results of [Reference Mantovani and Metere23, Reference Martins-Ferreira and Van der Linden24] with the fact that any variety of non-associative ${\mathbb {K}}$![]() -algebras is a category of groups with operations in the sense of [Reference Porter27], we see that this interpretation holds in the context where we are working. So here, ${\mathit {Rep}}(B,\,X)={\mathit {Act}}(B,\,X)$
-algebras is a category of groups with operations in the sense of [Reference Porter27], we see that this interpretation holds in the context where we are working. So here, ${\mathit {Rep}}(B,\,X)={\mathit {Act}}(B,\,X)$![]() when $X$
when $X$![]() is an abelian object.
is an abelian object.
In the case of Lie algebras, we regain the classical concept of a Lie algebra representation, which is often defined as a morphism $B\to \mathfrak {gl}(X)$![]() , where $\mathfrak {gl}(X)$
, where $\mathfrak {gl}(X)$![]() is the Lie algebra of linear endomorphisms of the vector space $X$
is the Lie algebra of linear endomorphisms of the vector space $X$![]() . For $f$
. For $f$![]() , $g\colon X\to X$
, $g\colon X\to X$![]() , the bracket $[f,\,g]=f {\scriptstyle {\circ }} g-g {\scriptstyle {\circ }} f$
, the bracket $[f,\,g]=f {\scriptstyle {\circ }} g-g {\scriptstyle {\circ }} f$![]() is a Lie algebra structure on ${\mathit {Hom}}(X,\,X)$
is a Lie algebra structure on ${\mathit {Hom}}(X,\,X)$![]() , because composition of endomorphisms is associative.
, because composition of endomorphisms is associative.
As we shall see below, it makes sense to restrict the representability condition from actions to representations, as follows: we say that ${\mathcal {V}}$![]() has representable representations when for each abelian algebra $X$
has representable representations when for each abelian algebra $X$![]() , the contravariant functor
, the contravariant functor
that sends an algebra $B$![]() to the set of $B$
to the set of $B$![]() -module structures on $X$
-module structures on $X$![]() is a representable functor.
is a representable functor.
For instance, if ${\mathcal {V}}={\mathsf {Lie}}_{{\mathbb {K}}}$![]() , then ${\mathit {Rep}}(-,X)$
, then ${\mathit {Rep}}(-,X)$![]() is represented by $\mathfrak {gl}(X)$
is represented by $\mathfrak {gl}(X)$![]() , which means ${\mathit {Rep}}(-,X)\cong {\mathit {Hom}}(-,\mathfrak {gl}(X))$
, which means ${\mathit {Rep}}(-,X)\cong {\mathit {Hom}}(-,\mathfrak {gl}(X))$![]() . On the other hand, the proof of Proposition 1.9 can be used to show that the variety of associative algebras does not have representable representations.
. On the other hand, the proof of Proposition 1.9 can be used to show that the variety of associative algebras does not have representable representations.
This condition is clearly weaker than action representability; it will, however, turn out to be sufficient for our purposes. Of course, everything we said above about actions stays valid for representations.
2 Algebraic coherence
A first step towards the main result of this paper is proving that in the context of non-associative algebras, action representability/representability of representations implies a condition called algebraic coherence [Reference Cigoli, Gray and Van der Linden10]. The reason we want this comes from the fact that an algebraically coherent variety satisfies some identities of degree three, useful in the next sections. From [Reference García-Martínez and Van der Linden15], we have the following characterization:
Theorem 2.1 Let ${\mathbb {K}}$![]() be an infinite field. If ${\mathcal {V}}$
be an infinite field. If ${\mathcal {V}}$![]() is a variety of non-associative ${\mathbb {K}}$
is a variety of non-associative ${\mathbb {K}}$![]() -algebras, then the following conditions are equivalent:
-algebras, then the following conditions are equivalent:
(i) ${\mathcal {V}}$
 is algebraically coherent;
is algebraically coherent;(ii) ${\mathcal {V}}$
 is an Orzech category of interest [Reference Orzech26];
is an Orzech category of interest [Reference Orzech26];(iii) ${\mathcal {V}}$
 is a $2$
is a $2$ -variety: for any ideal $I$
-variety: for any ideal $I$ of an algebra $A$
of an algebra $A$ , the subalgebra $I^{2}$
, the subalgebra $I^{2}$ of $A$
of $A$ is again an ideal;
is again an ideal;(iv) there exist $\lambda _{1}$
 , …, $\lambda _{8}$
, …, $\lambda _{8}$ , $\mu _{1}$
, $\mu _{1}$ , …, $\mu _{8}$
, …, $\mu _{8}$ in ${\mathbb {K}}$
in ${\mathbb {K}}$ such that
\begin{align*} z(xy)& = \lambda_{1}(zx)y+\lambda_{2}(xz)y+ \lambda_{3}y(zx)+\lambda_{4}y(xz)\\ & \quad +\lambda_{5}(zy)x+\lambda_{6}(yz)x+ \lambda_{7}x(zy)+\lambda_{8}x(yz) \end{align*}and
such that
\begin{align*} z(xy)& = \lambda_{1}(zx)y+\lambda_{2}(xz)y+ \lambda_{3}y(zx)+\lambda_{4}y(xz)\\ & \quad +\lambda_{5}(zy)x+\lambda_{6}(yz)x+ \lambda_{7}x(zy)+\lambda_{8}x(yz) \end{align*}and \begin{align*} (xy)z& = \mu_{1}(zx)y+\mu_{2}(xz)y+ \mu_{3}y(zx)+\mu_{4}y(xz)\\ & \quad+\mu_{5}(zy)x+\mu_{6}(yz)x+ \mu_{7}x(zy)+\mu_{8}x(yz) \end{align*}are identities in ${\mathcal {V}}$
\begin{align*} (xy)z& = \mu_{1}(zx)y+\mu_{2}(xz)y+ \mu_{3}y(zx)+\mu_{4}y(xz)\\ & \quad+\mu_{5}(zy)x+\mu_{6}(yz)x+ \mu_{7}x(zy)+\mu_{8}x(yz) \end{align*}are identities in ${\mathcal {V}}$
 .
.
We call those two identities together the $\lambda /\mu$![]() -rules. One should understand them as some ‘general associativity rules’. We remark that the case where $\lambda _1=1=\mu _8$
-rules. One should understand them as some ‘general associativity rules’. We remark that the case where $\lambda _1=1=\mu _8$![]() and the other coefficients are zero is just associativity. It is easy to see that the Jacobi identity is another particular case of the $\lambda /\mu$
and the other coefficients are zero is just associativity. It is easy to see that the Jacobi identity is another particular case of the $\lambda /\mu$![]() -rules.
-rules.
Theorem 2.2 Let ${\mathbb {K}}$![]() be an infinite field and ${\mathcal {V}}$
be an infinite field and ${\mathcal {V}}$![]() be a variety of non-associative algebras over ${\mathbb {K}}$
be a variety of non-associative algebras over ${\mathbb {K}}$![]() . If ${\mathcal {V}}$
. If ${\mathcal {V}}$![]() has representable representations, then it is an algebraically coherent category.
has representable representations, then it is an algebraically coherent category.
Proof. Consider the free non-associative algebra on the set $\{b,\, b',\, x\}$![]() . We quotient it by the ideal $I$
. We quotient it by the ideal $I$![]() generated by $xb$
generated by $xb$![]() , $bx$
, $bx$![]() , $b'x$
, $b'x$![]() , $xb'$
, $xb'$![]() , $xx$
, $xx$![]() , $bb$
, $bb$![]() , $b'b'$
, $b'b'$![]() and all monomials of degree $3$
and all monomials of degree $3$![]() or higher in which one of the variables $b$
or higher in which one of the variables $b$![]() , $b'$
, $b'$![]() , $x$
, $x$![]() is repeated. We reflect the result into the variety ${\mathcal {V}}$
is repeated. We reflect the result into the variety ${\mathcal {V}}$![]() by dividing out the ideal generated by the identities of ${\mathcal {V}}$
by dividing out the ideal generated by the identities of ${\mathcal {V}}$![]() and obtain an algebra $Q$
and obtain an algebra $Q$![]() . Since ${\mathbb {K}}$
. Since ${\mathbb {K}}$![]() is an infinite field, by Theorem 1.4, the sub-vector space generated by the classes of the elements of the form $(bb')x$
is an infinite field, by Theorem 1.4, the sub-vector space generated by the classes of the elements of the form $(bb')x$![]() (all possible permutations and bracketings) consists entirely of classes of linear combinations of such elements of degree $3$
(all possible permutations and bracketings) consists entirely of classes of linear combinations of such elements of degree $3$![]() . We call this vector space $A$
. We call this vector space $A$![]() , and view it as an abelian ${\mathbb {K}}$
, and view it as an abelian ${\mathbb {K}}$![]() -algebra.
-algebra.
We write $B$![]() for the abelian ${\mathcal {V}}$
for the abelian ${\mathcal {V}}$![]() -algebra generated by $b$
-algebra generated by $b$![]() , $B'$
, $B'$![]() for the abelian ${\mathcal {V}}$
for the abelian ${\mathcal {V}}$![]() -algebra generated by $b'$
-algebra generated by $b'$![]() and $C$
and $C$![]() for the free vector space generated by $c$
for the free vector space generated by $c$![]() , viewed as an abelian ${\mathbb {K}}$
, viewed as an abelian ${\mathbb {K}}$![]() -algebra. In ${\mathcal {V}}$
-algebra. In ${\mathcal {V}}$![]() , we then define a representation of $B + B'$
, we then define a representation of $B + B'$![]() on the abelian algebra $V=A\times C$
on the abelian algebra $V=A\times C$![]() by ${}^{b}a = 0 = a^{b}$
by ${}^{b}a = 0 = a^{b}$![]() , ${}^{b'}a = 0 = a^{b'}$
, ${}^{b'}a = 0 = a^{b'}$![]() , ${}^{bb'}a = {}^{b'b}a = 0 = a^{bb'} = a^{b'b}$
, ${}^{bb'}a = {}^{b'b}a = 0 = a^{bb'} = a^{b'b}$![]() where $a$
where $a$![]() is any element of $A$
is any element of $A$![]() , ${}^{b}c = 0 = c^{b}$
, ${}^{b}c = 0 = c^{b}$![]() , ${}^{b'}c = 0 = c^{b'}$
, ${}^{b'}c = 0 = c^{b'}$![]() and ${}^{bb'}c = (bb')x$
and ${}^{bb'}c = (bb')x$![]() , ${}^{b'b}c = (b'b)x$
, ${}^{b'b}c = (b'b)x$![]() , $c^{bb'} = x(bb')$
, $c^{bb'} = x(bb')$![]() , $c^{b'b} = x(b'b)$
, $c^{b'b} = x(b'b)$![]() . We need to verify that this does indeed determine an action. To do so, let us give an explicit description of the corresponding ${\mathcal {V}}$
. We need to verify that this does indeed determine an action. To do so, let us give an explicit description of the corresponding ${\mathcal {V}}$![]() -algebra morphism $\xi \colon (B+B')\flat V\to V$
-algebra morphism $\xi \colon (B+B')\flat V\to V$![]() . We first consider four ${\mathcal {V}}$
. We first consider four ${\mathcal {V}}$![]() -algebra morphisms $B+B'+A+C\to Q\times C$
-algebra morphisms $B+B'+A+C\to Q\times C$![]() , one which sends $\theta (b,\,b',\,a,\,c)$
, one which sends $\theta (b,\,b',\,a,\,c)$![]() – where $\theta$
– where $\theta$![]() is a polynomial in $n+3$
is a polynomial in $n+3$![]() variables and $a\in A^{n}$
variables and $a\in A^{n}$![]() for some $n\in {\mathbb {N}}$
for some $n\in {\mathbb {N}}$![]() – to $(\theta (b,\,b',\,0,\,x),\,0)$
– to $(\theta (b,\,b',\,0,\,x),\,0)$![]() , and three others, which send it to $(\theta (0,\,0,\,a,\,0),\,0)$
, and three others, which send it to $(\theta (0,\,0,\,a,\,0),\,0)$![]() , $(\theta (0,\,0,\,0,\,x),\,0)$
, $(\theta (0,\,0,\,0,\,x),\,0)$![]() and $(0,\,\theta (0,\,0,\,0,\,c))$
and $(0,\,\theta (0,\,0,\,0,\,c))$![]() , respectively. We combine them into the ${\mathbb {K}}$
, respectively. We combine them into the ${\mathbb {K}}$![]() -linear map
-linear map
Since this map vanishes on monomials in $a$![]() and $c$
and $c$![]() that contain at least one element of $A$
that contain at least one element of $A$![]() and one $c$
and one $c$![]() , it factors through the quotient
, it factors through the quotient
to a ${\mathbb {K}}$![]() -linear map $(B+B')+V\to Q\times C$
-linear map $(B+B')+V\to Q\times C$![]() , which in turn restricts to a ${\mathbb {K}}$
, which in turn restricts to a ${\mathbb {K}}$![]() -linear map $(B+B')\flat V\to Q\times C$
-linear map $(B+B')\flat V\to Q\times C$![]() . It is easy to check that this map factors over the inclusion of $A\times C=V$
. It is easy to check that this map factors over the inclusion of $A\times C=V$![]() into $Q\times C$
into $Q\times C$![]() . The resulting factorization is a ${\mathbb {K}}$
. The resulting factorization is a ${\mathbb {K}}$![]() -linear map $\xi \colon (B+B')\flat V\to V$
-linear map $\xi \colon (B+B')\flat V\to V$![]() , which is actually a morphism of ${\mathbb {K}}$
, which is actually a morphism of ${\mathbb {K}}$![]() -algebras, because it sends all binary products in $(B+B')\flat V$
-algebras, because it sends all binary products in $(B+B')\flat V$![]() to zero, as it should. We may now check that $\xi$
to zero, as it should. We may now check that $\xi$![]() satisfies the axioms of a $B\flat (-)$
satisfies the axioms of a $B\flat (-)$![]() -algebra, which follows immediately from the definitions – see 1.2.
-algebra, which follows immediately from the definitions – see 1.2.
Since ${\mathcal {V}}$![]() has representable representations in ${\mathcal {V}}$
has representable representations in ${\mathcal {V}}$![]() , the action $\xi$
, the action $\xi$![]() is necessarily zero, because that is where it is sent by the canonical isomorphism
is necessarily zero, because that is where it is sent by the canonical isomorphism
defined by restricting an action of $B+B'$![]() on $V$
on $V$![]() to an action of $B$
to an action of $B$![]() on $V$
on $V$![]() together with an action of $B'$
together with an action of $B'$![]() on $V$
on $V$![]() . It follows that $(bb')x$
. It follows that $(bb')x$![]() , $(b'b)x$
, $(b'b)x$![]() , $x(bb')$
, $x(bb')$![]() and $x(b'b)$
and $x(b'b)$![]() vanish in $A$
vanish in $A$![]() . This means that the identities of ${\mathcal {V}}$
. This means that the identities of ${\mathcal {V}}$![]() allow us to write each of them as a linear combination of some degree $3$
allow us to write each of them as a linear combination of some degree $3$![]() elements of the ideal $I$
elements of the ideal $I$![]() , which can only mean that the $\lambda /\mu$
, which can only mean that the $\lambda /\mu$![]() -rules hold in ${\mathcal {V}}$
-rules hold in ${\mathcal {V}}$![]() . In other words, ${\mathcal {V}}$
. In other words, ${\mathcal {V}}$![]() is algebraically coherent.
is algebraically coherent.
Remark 2.3 If in Theorem 2.2 the variety ${\mathcal {V}}$![]() has representable actions, then an alternate proof may be given, which uses that action representability implies a weaker condition called action accessibility [Reference Bourn and Janelidze6]. As it turns out, a variety of non-associative algebras over an infinite field is action accessible if and only if it satisfies the equivalent conditions of Theorem 2.1. Indeed, as A. Montoli proved in [Reference Montoli25], all Orzech categories of interest are action accessible, which yields one implication. The converse makes non-trivial use of Lemma 2.9 in [Reference Cigoli, Mantovani and Metere11].
has representable actions, then an alternate proof may be given, which uses that action representability implies a weaker condition called action accessibility [Reference Bourn and Janelidze6]. As it turns out, a variety of non-associative algebras over an infinite field is action accessible if and only if it satisfies the equivalent conditions of Theorem 2.1. Indeed, as A. Montoli proved in [Reference Montoli25], all Orzech categories of interest are action accessible, which yields one implication. The converse makes non-trivial use of Lemma 2.9 in [Reference Cigoli, Mantovani and Metere11].
3 Identities of degree two
We proved that from the representability of representations, we may deduce certain identities of degree three. The goal of this section is to go for the identities of degree two necessary to obtain Lie algebras. In fact, action representability does not characterize the Jacobi identity alone, since the variety ${\mathsf {Leib}}_{{\mathbb {K}}}$![]() of Leibniz algebras over ${\mathbb {K}}$
of Leibniz algebras over ${\mathbb {K}}$![]() is not action representable in general. This observation comes from Theorem 5.5 of [Reference Casas and Ladra9], but it is possible to give a proof, similar to the one of Proposition 1.9, showing that ${\mathsf {Leib}}_{{\mathbb {K}}}$
is not action representable in general. This observation comes from Theorem 5.5 of [Reference Casas and Ladra9], but it is possible to give a proof, similar to the one of Proposition 1.9, showing that ${\mathsf {Leib}}_{{\mathbb {K}}}$![]() does not have representable representations.
does not have representable representations.
We are now going to show that any variety of non-associative algebras with representable representations over an infinite field satisfies non-trivial identities of degree two. We start with fields of characteristic zero in Proposition 3.1 and continue with fields of prime characteristic in Proposition 3.4.
Our main technique is to obtain a system of polynomial equations, which we then prove is inconsistent. To do so, we use computer algebra in two distinct ways: first, we need to produce the system of equations itself; due to the complexity of the manipulations needed here, we preferred to do this on a computer, rather than by hand: see below and [Reference García-Martínez, Tsishyn, Van der Linden and Vienne14] where this is explained in further detail. Next, the system of equations thus obtained has to be shown inconsistent. The size of the system makes it impossible to do this by hand; we used the open-source software package Singular [Reference Decker, Greuel, Pfister and Schönemann12] which gives us an explicit reason for the system's inconsistency. How this is done is explained below. Part of the code used is displayed in Figure 1, and the full code and its output are accessible as a set of ancillary files in the arXiv version of our paper.
Proposition 3.1 Let ${\mathbb {K}}$![]() be a field of characteristic $0$
be a field of characteristic $0$![]() and ${\mathcal {V}}$
and ${\mathcal {V}}$![]() be a variety of non-associative algebras over ${\mathbb {K}}$
be a variety of non-associative algebras over ${\mathbb {K}}$![]() . If ${\mathcal {V}}$
. If ${\mathcal {V}}$![]() has representable representations, then ${\mathcal {V}}$
has representable representations, then ${\mathcal {V}}$![]() satisfies a non-trivial identity of degree two.
satisfies a non-trivial identity of degree two.

Figure 1. Singular code.
Proof. Let us assume that ${\mathcal {V}}$![]() is a variety with representable representations, all of whose non-trivial identities are of degree three or higher. From Theorem 2.2, we already know that ${\mathcal {V}}$
is a variety with representable representations, all of whose non-trivial identities are of degree three or higher. From Theorem 2.2, we already know that ${\mathcal {V}}$![]() satisfies the $\lambda / \mu$
satisfies the $\lambda / \mu$![]() -rules. The strategy of this proof is to show that representability of representations forces the coefficients $\lambda _i$
-rules. The strategy of this proof is to show that representability of representations forces the coefficients $\lambda _i$![]() and $\mu _i$
and $\mu _i$![]() to satisfy a specific system of polynomial equations whose set of solutions is empty (unless some degree two identities are satisfied, but we assumed that it is not the case). This then means that algebraic coherence, and therefore representability of representations, cannot hold in ${\mathcal {V}}$
to satisfy a specific system of polynomial equations whose set of solutions is empty (unless some degree two identities are satisfied, but we assumed that it is not the case). This then means that algebraic coherence, and therefore representability of representations, cannot hold in ${\mathcal {V}}$![]() – which is a contradiction.
– which is a contradiction.
In order to do so, we let $X$![]() be the $79$
be the $79$![]() -dimensional abelian algebra generated by the elements $\{x,\, y^{i}_\alpha, z^{ij}_{\alpha \beta } ,\,t^{ijk}_{\alpha \beta \gamma }\mid \alpha ,\beta ,\gamma \in \{ r,l\} \text{ and } (i\; j\; k) \in S_3\}$
-dimensional abelian algebra generated by the elements $\{x,\, y^{i}_\alpha, z^{ij}_{\alpha \beta } ,\,t^{ijk}_{\alpha \beta \gamma }\mid \alpha ,\beta ,\gamma \in \{ r,l\} \text{ and } (i\; j\; k) \in S_3\}$![]() , where $r$
, where $r$![]() stands for right and $l$
stands for right and $l$![]() for left, while $i$
for left, while $i$![]() , $j$
, $j$![]() , $k\in \{1,\,2,\,3\}$
, $k\in \{1,\,2,\,3\}$![]() are pairwise non-equal. Furthermore, $B^{i}$
are pairwise non-equal. Furthermore, $B^{i}$![]() is the abelian algebra generated by $b^{i}$
is the abelian algebra generated by $b^{i}$![]() , for $i \in \{ 1,\,2,\,3\}$
, for $i \in \{ 1,\,2,\,3\}$![]() . Those algebras are in ${\mathcal {V}}$
. Those algebras are in ${\mathcal {V}}$![]() because they are abelian. We now define (abelian) actions of the algebras $B^{i}$
because they are abelian. We now define (abelian) actions of the algebras $B^{i}$![]() on $X$
on $X$![]() :
:

while $b^{i} t^{jkm}_{\alpha \beta \gamma }=t^{jkm}_{\alpha \beta \gamma }b^{i} =0$![]() . Those actions are well defined. Indeed, the $\lambda / \mu$
. Those actions are well defined. Indeed, the $\lambda / \mu$![]() -rules are satisfied since any product of three elements in the semi-direct product $B^{i} \ltimes X$
-rules are satisfied since any product of three elements in the semi-direct product $B^{i} \ltimes X$![]() vanishes. In order to familiarize ourselves with those actions which will appear again later, we first give some examples of their behaviour in $(B^{1}+B^{2}+B^{3})\ltimes X$
vanishes. In order to familiarize ourselves with those actions which will appear again later, we first give some examples of their behaviour in $(B^{1}+B^{2}+B^{3})\ltimes X$![]() :
:
Next, as explained in § 1, by representability of representations the semi-direct product $(B^{1}+B^{2}+B^{3})\ltimes X$![]() is in ${\mathcal {V}}$
is in ${\mathcal {V}}$![]() and thus all elements of this semi-direct product have to satisfy the $\lambda / \mu$
and thus all elements of this semi-direct product have to satisfy the $\lambda / \mu$![]() -rules. We construct an equational system on the $\lambda _i$
-rules. We construct an equational system on the $\lambda _i$![]() and $\mu _i$
and $\mu _i$![]() whose set of solutions is empty, by checking the $\lambda / \mu$
whose set of solutions is empty, by checking the $\lambda / \mu$![]() -rules for some specific elements. For example, since $(xb^{1})b^{2}$
-rules for some specific elements. For example, since $(xb^{1})b^{2}$![]() is in $(B^{1}+B^{2}+B^{3})\ltimes X$
is in $(B^{1}+B^{2}+B^{3})\ltimes X$![]() , decomposing it a first time gives:
, decomposing it a first time gives:

Then we apply the $\lambda / \mu$![]() -rules again on the monomials where $x$
-rules again on the monomials where $x$![]() is isolated and write everything on the same side. This gives us a linear combination $\sum \nolimits f_k(\lambda _i,\,\mu _j) z^{ij}_{\alpha \beta }$
is isolated and write everything on the same side. This gives us a linear combination $\sum \nolimits f_k(\lambda _i,\,\mu _j) z^{ij}_{\alpha \beta }$![]() which must be equal to zero. Since the $z^{ij}_{\alpha \beta }$
which must be equal to zero. Since the $z^{ij}_{\alpha \beta }$![]() are linearly independent, all the polynomials $f_k\in {\mathbb {Q}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$
are linearly independent, all the polynomials $f_k\in {\mathbb {Q}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$![]() vanish. Following this procedure for $(xb^{1})b^{2}$
vanish. Following this procedure for $(xb^{1})b^{2}$![]() gives us the eight first polynomials of Figure 1 (lines 2–9, written in Singular [Reference Decker, Greuel, Pfister and Schönemann12] code). To compute the $f_k$
gives us the eight first polynomials of Figure 1 (lines 2–9, written in Singular [Reference Decker, Greuel, Pfister and Schönemann12] code). To compute the $f_k$![]() for $k=9$
for $k=9$![]() , …, $32$
, …, $32$![]() , we repeat this procedure on the elements $(b^{1}x)b^{2}$
, we repeat this procedure on the elements $(b^{1}x)b^{2}$![]() , $b^{2}(b^{1}x)$
, $b^{2}(b^{1}x)$![]() and $b^{2}(xb^{1})$
and $b^{2}(xb^{1})$![]() . The details of the computations are done and explained in [Reference García-Martínez, Tsishyn, Van der Linden and Vienne14].
. The details of the computations are done and explained in [Reference García-Martínez, Tsishyn, Van der Linden and Vienne14].
Next, we use the fact that $(b^{1}b^{2})b^{3}$![]() and $b^{1}(b^{2}b^{3})$
and $b^{1}(b^{2}b^{3})$![]() should also satisfy the $\lambda /\mu$
should also satisfy the $\lambda /\mu$![]() -rules since they are elements of $(B^{1}+B^{2}+B^{3})\ltimes X$
-rules since they are elements of $(B^{1}+B^{2}+B^{3})\ltimes X$![]() . Making the decomposition work on $(b^{1}(b^{2}b^{3}))x$
. Making the decomposition work on $(b^{1}(b^{2}b^{3}))x$![]() , $x(b^{1}(b^{2}b^{3}))$
, $x(b^{1}(b^{2}b^{3}))$![]() , $((b^{1}b^{2})b^{3})x$
, $((b^{1}b^{2})b^{3})x$![]() and $x((b^{1}b^{2})b^{3})$
and $x((b^{1}b^{2})b^{3})$![]() – again, a procedure explained in [Reference García-Martínez, Tsishyn, Van der Linden and Vienne14] – we find the last 192 polynomials in the system of equations.
– again, a procedure explained in [Reference García-Martínez, Tsishyn, Van der Linden and Vienne14] – we find the last 192 polynomials in the system of equations.
Finally, we employ the computer algebra system Singular [Reference Decker, Greuel, Pfister and Schönemann12], which uses Gröbner bases, to look for a common root of the polynomials. Based on the code in Figure 1, the computer system tells us that $1$![]() is a linear combination in ${\mathbb {Q}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$
is a linear combination in ${\mathbb {Q}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$![]() of the polynomials $f_{1}$
of the polynomials $f_{1}$![]() , …, $f_{224}$
, …, $f_{224}$![]() . The arXiv version of this paper includes an ancillary file containing an explicit way to write $1$
. The arXiv version of this paper includes an ancillary file containing an explicit way to write $1$![]() as a linear combination of the $(f_i)_i$
as a linear combination of the $(f_i)_i$![]() in ${\mathbb {Q}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$
in ${\mathbb {Q}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$![]() . Hence the set of solutions of the polynomial system is empty, which completes the proof.
. Hence the set of solutions of the polynomial system is empty, which completes the proof.
Remark 3.2 The parameter dp in line 1 means that degree reverse lexicographical ordering of polynomials is chosen. This choice does not have any impact in the proof other than the efficiency of the computation.
Remark 3.3 The system of equations in Figure 1 is not the smallest inconsistent system of equations involving the $\lambda _i$![]() and $\mu _i$
and $\mu _i$![]() . For instance, from the output in the ancillary files, it is immediately clear that $f_{140}$
. For instance, from the output in the ancillary files, it is immediately clear that $f_{140}$![]() can be removed from the system while maintaining its inconsistency. Actually, the system may be reduced significantly: we checked that equations number $1$
can be removed from the system while maintaining its inconsistency. Actually, the system may be reduced significantly: we checked that equations number $1$![]() , $3$
, $3$![]() , $4$
, $4$![]() , $6$
, $6$![]() , $7$
, $7$![]() , $10$
, $10$![]() , $11$
, $11$![]() , $12$
, $12$![]() , $13$
, $13$![]() , $14$
, $14$![]() , $15$
, $15$![]() , $16$
, $16$![]() , $17$
, $17$![]() , $18$
, $18$![]() , $19$
, $19$![]() , $20$
, $20$![]() , $22$
, $22$![]() , $23$
, $23$![]() , $25$
, $25$![]() , $26$
, $26$![]() , $27$
, $27$![]() , $28$
, $28$![]() , $29$
, $29$![]() , $30$
, $30$![]() , $31$
, $31$![]() , $33$
, $33$![]() , $34$
, $34$![]() , $35$
, $35$![]() , $36$
, $36$![]() , $37$
, $37$![]() , $38$
, $38$![]() , $39$
, $39$![]() , $40$
, $40$![]() , $41$
, $41$![]() , $42$
, $42$![]() , $43$
, $43$![]() , $44$
, $44$![]() , $45$
, $45$![]() , $46$
, $46$![]() , $47$
, $47$![]() , $49$
, $49$![]() , $56$
, $56$![]() , $82$
, $82$![]() , $92$
, $92$![]() together still form an inconsistent system of polynomial equations. However, giving the explicit polynomials that prove the system's inconsistency becomes harder as its size goes down.
together still form an inconsistent system of polynomial equations. However, giving the explicit polynomials that prove the system's inconsistency becomes harder as its size goes down.
In order to have the result for all infinite fields, we extend this to prime characteristics. The proof needs fine-tuning since in characteristic zero rational coefficients are allowed, something which is not the case in prime characteristic.
Proposition 3.4 Let ${\mathbb {K}}$![]() be an infinite field of prime characteristic and ${\mathcal {V}}$
be an infinite field of prime characteristic and ${\mathcal {V}}$![]() a variety of non-associative algebras over ${\mathbb {K}}$
a variety of non-associative algebras over ${\mathbb {K}}$![]() . If ${\mathcal {V}}$
. If ${\mathcal {V}}$![]() has representable representations, then ${\mathcal {V}}$
has representable representations, then ${\mathcal {V}}$![]() satisfies a non-trivial identity of degree two.
satisfies a non-trivial identity of degree two.
Proof. In this proof, we mimic the trick used in Theorem 4.2 of [Reference García-Martínez and Van der Linden16]. Indeed, in the proof of Proposition 3.1, we wrote $1$![]() as a linear combination of the $(f_i)_{1\leq i\leq 224}$
as a linear combination of the $(f_i)_{1\leq i\leq 224}$![]() in ${\mathbb {Q}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$
in ${\mathbb {Q}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$![]() . Instead of doing this, we will write some $m\in {\mathbb {N}}$
. Instead of doing this, we will write some $m\in {\mathbb {N}}$![]() as a linear combination in ${\mathbb {Z}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$
as a linear combination in ${\mathbb {Z}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$![]() of these 224 polynomials because, then, we will just have to check that the system has an empty set of solutions for all infinite fields whose characteristic divides $m$
of these 224 polynomials because, then, we will just have to check that the system has an empty set of solutions for all infinite fields whose characteristic divides $m$![]() . The problem is that the natural number $m$
. The problem is that the natural number $m$![]() , equal to ${145679959084559802430969530553780449546315662406534685329857227}$
, equal to ${145679959084559802430969530553780449546315662406534685329857227}$![]() ${0548680472045472116250386006867468944668940571897397172623649920632890267296075654343504}$
${0548680472045472116250386006867468944668940571897397172623649920632890267296075654343504}$![]() ${20878447841877721000590295768558884307124148778177377876830064916666592523291}$
${20878447841877721000590295768558884307124148778177377876830064916666592523291}$![]() ${59304174905496937087738581344349487066880186556945585175775695576209957462932}$
${59304174905496937087738581344349487066880186556945585175775695576209957462932}$![]() ${78480812431412260574404024455598320441859722042018260900473969846828608645627}$
${78480812431412260574404024455598320441859722042018260900473969846828608645627}$![]() ${87183059873566162910333424228212906065894343670540539725147842861513488173278}$
${87183059873566162910333424228212906065894343670540539725147842861513488173278}$![]() ${22021774577694196501188227813156363270426620366150688257342489840683094034209}$
${22021774577694196501188227813156363270426620366150688257342489840683094034209}$![]() ${50318}$
${50318}$![]() , which we find with a first computation in Singular is 541 digits long. This makes finding its prime divisors very difficult. The trick is to compute the Gröbner basis with a different monomial order. This will give us another natural number $m'$
, which we find with a first computation in Singular is 541 digits long. This makes finding its prime divisors very difficult. The trick is to compute the Gröbner basis with a different monomial order. This will give us another natural number $m'$![]() and we will only need to check the inconsistency of the system of equations for the common prime divisors of $m$
and we will only need to check the inconsistency of the system of equations for the common prime divisors of $m$![]() and $m'$
and $m'$![]() . A different monomial order may be chosen in line 1 of the code in Figure 1: for instance, swapping $\mu _7$
. A different monomial order may be chosen in line 1 of the code in Figure 1: for instance, swapping $\mu _7$![]() and $\mu _8$
and $\mu _8$![]() is expressed as
is expressed as
ring r=0,(x(1..8),y(1..6),y(8),y(7)),dp;
This leads us to the number $m'$![]() which is equal to ${525717631958791658273542822932875536277944482117059047298355615522}$
which is equal to ${525717631958791658273542822932875536277944482117059047298355615522}$![]() ${4447303866073034964879226451745451233297544838}$
${4447303866073034964879226451745451233297544838}$![]() ${18964761098115453534593150454043600868151586630528071290312031929148817936277}$
${18964761098115453534593150454043600868151586630528071290312031929148817936277}$![]() ${58784552281330948466297460892213124611259557307705714671224295558125970110748}$
${58784552281330948466297460892213124611259557307705714671224295558125970110748}$![]() ${22233317864875426854341643972018163355893297334149632686212253120055566461120}$
${22233317864875426854341643972018163355893297334149632686212253120055566461120}$![]() ${4869818358}$
${4869818358}$![]() and only 353 digits long. Obviously, $2$
and only 353 digits long. Obviously, $2$![]() is a common prime divisor. Using the Euclidean algorithm, it is rapidly seen that it is the only one. In order to conclude, we prove as before, using Singular, that $I = {\mathbb {K}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$
is a common prime divisor. Using the Euclidean algorithm, it is rapidly seen that it is the only one. In order to conclude, we prove as before, using Singular, that $I = {\mathbb {K}}[\lambda _1,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$![]() for any field ${\mathbb {K}}$
for any field ${\mathbb {K}}$![]() of characteristic $2$
of characteristic $2$![]() , where $I$
, where $I$![]() is the ideal of ${\mathbb {K}} [\lambda _1 ,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$
is the ideal of ${\mathbb {K}} [\lambda _1 ,\, \ldots ,\, \lambda _8,\, \mu _1,\, \ldots ,\, \mu _8]$![]() generated by the polynomials $f_k$
generated by the polynomials $f_k$![]() for $k=1$
for $k=1$![]() , …, $224$
, …, $224$![]() . This is done in Singular by using
. This is done in Singular by using
ring r=2,(x(1..8),y(1..8)),dp;
in line 1 of the code in Figure 1. Again, explicit linear combinations are given in the arXiv version of this paper as an ancillary file.
Corollary 3.5 If ${\mathcal {V}}$![]() is a variety of non-associative algebras over an infinite field whose representations are representable, then ${\mathcal {V}}$
is a variety of non-associative algebras over an infinite field whose representations are representable, then ${\mathcal {V}}$![]() is either a subvariety of the variety of commutative algebras, or a subvariety of the variety of anticommutative algebras.
is either a subvariety of the variety of commutative algebras, or a subvariety of the variety of anticommutative algebras.
Proof. Combine the above with Proposition 1.3.
4 Anticommutativity and the Jacobi identity
The last proposition of the previous section gives us two identities: commutativity and anticommutativity. The goal of this section is to show that representability of representations rules out the first case. Next, we will prove that from anticommutativity and the $\lambda /\mu$![]() -rules (which are both consequences of representability of representations), we can deduce that if the variety is non-abelian, then it has to satisfy the Jacobi identity.
-rules (which are both consequences of representability of representations), we can deduce that if the variety is non-abelian, then it has to satisfy the Jacobi identity.
Proposition 4.1 Let ${\mathcal {V}}$![]() be a variety of non-associative algebras over an infinite field of characteristic different from $2$
be a variety of non-associative algebras over an infinite field of characteristic different from $2$![]() . If ${\mathcal {V}}$
. If ${\mathcal {V}}$![]() is a variety of commutative algebras whose representations are representable, then it is an abelian variety.
is a variety of commutative algebras whose representations are representable, then it is an abelian variety.
Proof. First, since ${\mathcal {V}}$![]() has representable representations, it is algebraically coherent by Theorem 2.2. Hence the $\lambda / \mu$
has representable representations, it is algebraically coherent by Theorem 2.2. Hence the $\lambda / \mu$![]() -rules hold. By commutativity, these can be rewritten as
-rules hold. By commutativity, these can be rewritten as
for some $\lambda$![]() , $\mu \in {\mathbb {K}}$
, $\mu \in {\mathbb {K}}$![]() .
.
Now we need to use essentially the same algebras and actions as in the proof of Proposition 3.1, but without considerations for left and right, so that the actions satisfy the commutativity rule. In other words, for all $b^{i}$![]() in $B^{i}$
in $B^{i}$![]() and $w$
and $w$![]() in $X$
in $X$![]() we define the actions such that $bw=wb$
we define the actions such that $bw=wb$![]() . Such actions are well defined, and thus the semi-direct product $(B^{1}+B^{2}+B^{3})\ltimes X$
. Such actions are well defined, and thus the semi-direct product $(B^{1}+B^{2}+B^{3})\ltimes X$![]() is an object of ${\mathcal {V}}$
is an object of ${\mathcal {V}}$![]() by representability of representations. Therefore, its elements should satisfy the identity (†). Let us check this on $b^{1}(b^{2}x)$
by representability of representations. Therefore, its elements should satisfy the identity (†). Let us check this on $b^{1}(b^{2}x)$![]() : indeed, $b^{1}(b^{2}x) = \lambda (b^{1}b^{2})x + \mu b^{2}(b^{1}x) = \lambda ^{2} (xb^{1})b^{2} +\lambda \mu b^{1}(xb^{2})$
: indeed, $b^{1}(b^{2}x) = \lambda (b^{1}b^{2})x + \mu b^{2}(b^{1}x) = \lambda ^{2} (xb^{1})b^{2} +\lambda \mu b^{1}(xb^{2})$![]() , so that $0=(\lambda ^{2} + \mu ) z^{12} + (\lambda \mu -1) z^{21}$
, so that $0=(\lambda ^{2} + \mu ) z^{12} + (\lambda \mu -1) z^{21}$![]() . By linear independence of $\{z^{12},\,z^{21}\}$
. By linear independence of $\{z^{12},\,z^{21}\}$![]() , either ${\mathcal {V}}$
, either ${\mathcal {V}}$![]() is abelian or $\lambda = \mu = -1$
is abelian or $\lambda = \mu = -1$![]() .
.
The second case would mean that the identity (†) is now
Therefore, since $b^{1}(b^{2}b^{3})$![]() is an element of the semi-direct product we have that $b^{1}(b^{2}b^{3})= -(b^{1}b^{2})b^{3} - b^{2}(b^{1}b^{3})$
is an element of the semi-direct product we have that $b^{1}(b^{2}b^{3})= -(b^{1}b^{2})b^{3} - b^{2}(b^{1}b^{3})$![]() as an action, and in particular on $x$
as an action, and in particular on $x$![]() this implies
this implies
Decomposing each element on the left side and on the right side twice by applying (‡) gives us $t^{123} + t^{132} + t^{231} + t^{321} = - t^{312} - t^{321} - t^{123} - t^{213} - t^{213} - t^{231} - t^{132} - t^{312}$![]() , which is equivalent to $2t^{312} + 2t^{321} + 2t^{123} + 2t^{213} + 2t^{132} + 2t^{231}= 0$
, which is equivalent to $2t^{312} + 2t^{321} + 2t^{123} + 2t^{213} + 2t^{132} + 2t^{231}= 0$![]() . Since ${\mathit {char}}({\mathbb {K}}) \neq 2$
. Since ${\mathit {char}}({\mathbb {K}}) \neq 2$![]() and all these elements are linearly independent, we encounter a contradiction. Hence ${\mathcal {V}}$
and all these elements are linearly independent, we encounter a contradiction. Hence ${\mathcal {V}}$![]() is abelian.
is abelian.
Remark 4.2 If ${\mathit {char}}({\mathbb {K}})=2$![]() , then commutativity and anticommutativity are the same condition. Therefore, we do not have to care about it to state our next result. However, one should remember that quasi-Lie algebras and Lie algebras do not coincide when the characteristic of the field is $2$
, then commutativity and anticommutativity are the same condition. Therefore, we do not have to care about it to state our next result. However, one should remember that quasi-Lie algebras and Lie algebras do not coincide when the characteristic of the field is $2$![]() .
.
Proposition 4.3 Let ${\mathbb {K}}$![]() be an infinite field and ${\mathcal {V}}$
be an infinite field and ${\mathcal {V}}$![]() a variety of non-associative algebras over ${\mathbb {K}}$
a variety of non-associative algebras over ${\mathbb {K}}$![]() that satisfies the $\lambda /\mu$
that satisfies the $\lambda /\mu$![]() -rules and anticommutativity. If ${\mathcal {V}}$
-rules and anticommutativity. If ${\mathcal {V}}$![]() has representable representations, then the Jacobi identity holds in ${\mathcal {V}}$
has representable representations, then the Jacobi identity holds in ${\mathcal {V}}$![]() .
.
Proof. Because of anticommutativity, the $\lambda / \mu$![]() -rules can be rewritten as
-rules can be rewritten as
for some $\lambda$![]() , $\mu \in {\mathbb {K}}$
, $\mu \in {\mathbb {K}}$![]() . We consider the actions we defined in the proof of Proposition 4.1, corrected for anticommutativity. So we decree that an element $b^{i}$
. We consider the actions we defined in the proof of Proposition 4.1, corrected for anticommutativity. So we decree that an element $b^{i}$![]() acting on the left is the same as $b^{i}$
acting on the left is the same as $b^{i}$![]() acting on the right times $-1$
acting on the right times $-1$![]() . For instance, $b^{1}y^{2}=-y^{2} b^{1}$
. For instance, $b^{1}y^{2}=-y^{2} b^{1}$![]() and $b^{2}x = -xb^{2}$
and $b^{2}x = -xb^{2}$![]() . In order to check the identity (§) on $b^{1}(b^{2}x)$
. In order to check the identity (§) on $b^{1}(b^{2}x)$![]() , we compute:
, we compute:
By linear independence, this yields the system $\mu - \lambda ^{2} =0$![]() , $1-\lambda \mu =0$
, $1-\lambda \mu =0$![]() whose solution is $\lambda =\mu =1$
whose solution is $\lambda =\mu =1$![]() . Thus (§) becomes the Jacobi identity.
. Thus (§) becomes the Jacobi identity.
Corollary 4.4 Let ${\mathcal {V}}$![]() be a variety of non-associative algebras over an infinite field ${\mathbb {K}}$
be a variety of non-associative algebras over an infinite field ${\mathbb {K}}$![]() . If ${\mathcal {V}}$
. If ${\mathcal {V}}$![]() has representable representations, then ${\mathcal {V}}$
has representable representations, then ${\mathcal {V}}$![]() is a subvariety of ${\mathsf {Lie}}_{\mathbb {K}}$
is a subvariety of ${\mathsf {Lie}}_{\mathbb {K}}$![]() or ${\mathsf {qLie}}_{\mathbb {K}}$
or ${\mathsf {qLie}}_{\mathbb {K}}$![]() if ${\mathit {char}}({\mathbb {K}})=2$
if ${\mathit {char}}({\mathbb {K}})=2$![]() , and a subvariety of ${\mathsf {Lie}}_{\mathbb {K}}$
, and a subvariety of ${\mathsf {Lie}}_{\mathbb {K}}$![]() otherwise.
otherwise.
5 What about subvarieties?
We concluded the previous section by saying that the only potential identities of degree two for varieties with representable representations are $xy=0$![]() , $xy=-yx$
, $xy=-yx$![]() and $xx=0$
and $xx=0$![]() , and that the Jacobi identity necessarily holds. The question we answer in this section is: ‘Did we miss any other identities?’ As we have already explained above, such identities would have to be of degree at least $3$
, and that the Jacobi identity necessarily holds. The question we answer in this section is: ‘Did we miss any other identities?’ As we have already explained above, such identities would have to be of degree at least $3$![]() . The next proposition proves that we cannot add any non-trivial identities without making the variety abelian.
. The next proposition proves that we cannot add any non-trivial identities without making the variety abelian.
Proposition 5.1 Let ${\mathbb {K}}$![]() be an infinite field and ${\mathcal {V}}$
be an infinite field and ${\mathcal {V}}$![]() be a subvariety of ${\mathsf {Lie}}_{\mathbb {K}}$
be a subvariety of ${\mathsf {Lie}}_{\mathbb {K}}$![]() or ${\mathsf {qLie}}_{\mathbb {K}}$
or ${\mathsf {qLie}}_{\mathbb {K}}$![]() determined by a collection of identities of degree 3 or higher. Then ${\mathcal {V}}$
determined by a collection of identities of degree 3 or higher. Then ${\mathcal {V}}$![]() is an abelian variety if and only if it has representable representations.
is an abelian variety if and only if it has representable representations.
Proof. Let ${\mathcal {V}}$![]() be a non-abelian variety of ${\mathbb {K}}$
be a non-abelian variety of ${\mathbb {K}}$![]() -algebras with representable representations. In the previous sections, it was explained that there are no identities of degree two besides $xy=-yx$
-algebras with representable representations. In the previous sections, it was explained that there are no identities of degree two besides $xy=-yx$![]() or $xx=0$
or $xx=0$![]() , and that the Jacobi identity holds. The idea here is to first prove that there is no identity of degree three besides Jacobi, and then we show that no other identities (of degree $n > 3$
, and that the Jacobi identity holds. The idea here is to first prove that there is no identity of degree three besides Jacobi, and then we show that no other identities (of degree $n > 3$![]() ) can hold.
) can hold.
First, suppose that ${\mathcal {V}}$![]() satisfies some degree three identities. Because of anticommutativity and Theorem 1.5, we may assume this identity to be $x(yz)= \lambda (xy)z + \mu y(xz)$
satisfies some degree three identities. Because of anticommutativity and Theorem 1.5, we may assume this identity to be $x(yz)= \lambda (xy)z + \mu y(xz)$![]() for certain $\lambda$
for certain $\lambda$![]() , $\mu \in {\mathbb {K}}$
, $\mu \in {\mathbb {K}}$![]() . Then we may recycle the ideas of the proof of Proposition 4.3 to reduce it to the Jacobi identity.
. Then we may recycle the ideas of the proof of Proposition 4.3 to reduce it to the Jacobi identity.
Now, the goal is to prove by induction that the existence of an identity of degree $n>3$![]() is in contradiction with Theorem 1.5. Let us assume that no other identities of degree lower than or equal to $n>3$
is in contradiction with Theorem 1.5. Let us assume that no other identities of degree lower than or equal to $n>3$![]() are satisfied. Let $\psi$
are satisfied. Let $\psi$![]() be a homogeneous identity of degree $n+1$
be a homogeneous identity of degree $n+1$![]() with $n>3$
with $n>3$![]() which holds in ${\mathcal {V}}$
which holds in ${\mathcal {V}}$![]() . We consider a non-trivial multilinear consequence $\varphi (x_1 ,\,\ldots ,\, x_n,\,x_0)=0$
. We consider a non-trivial multilinear consequence $\varphi (x_1 ,\,\ldots ,\, x_n,\,x_0)=0$![]() of $\psi$
of $\psi$![]() , whose existence is assured by Theorem 1.5. Using anticommutativity and the Jacobi identity, we can rewrite $\varphi$
, whose existence is assured by Theorem 1.5. Using anticommutativity and the Jacobi identity, we can rewrite $\varphi$![]() in the shape $0= \sum \nolimits _{i=1} \lambda _i \varphi _i (x_1 ,\, \ldots ,\, x_i x_0,\, \ldots ,\, x_n)$
in the shape $0= \sum \nolimits _{i=1} \lambda _i \varphi _i (x_1 ,\, \ldots ,\, x_i x_0,\, \ldots ,\, x_n)$![]() . We observe that if $\lambda _i=0$
. We observe that if $\lambda _i=0$![]() for all $i$
for all $i$![]() , then $\varphi$
, then $\varphi$![]() is just a consequence of $xy=-yx$
is just a consequence of $xy=-yx$![]() and $x(yz)+y(zx)+z(xy)=0$
and $x(yz)+y(zx)+z(xy)=0$![]() , or in other words a trivial identity. Note that it is impossible to be a consequence of other identities by the induction hypothesis. Proving that the $\lambda _i$
, or in other words a trivial identity. Note that it is impossible to be a consequence of other identities by the induction hypothesis. Proving that the $\lambda _i$![]() 's are zero will then bring us to a contradiction.
's are zero will then bring us to a contradiction.
We consider the same actions we used in Proposition 4.3 but extended to $n$![]() algebras $B^{i}$
algebras $B^{i}$![]() acting on $X$
acting on $X$![]() (which is also enlarged to more elements). Those are again well defined and thus we have that $(B^{1} + \ldots + B^{n}) \ltimes X$
(which is also enlarged to more elements). Those are again well defined and thus we have that $(B^{1} + \ldots + B^{n}) \ltimes X$![]() lies in ${\mathcal {V}}$
lies in ${\mathcal {V}}$![]() as already explained. Therefore the element $\psi ((b^{1},\,0),\,(b^{2},\,0),\, \ldots ,\, (b^{n},\,0),\,(0,\, x))=\psi (b^{1},\, \ldots ,\, b^{n},\,x)$
as already explained. Therefore the element $\psi ((b^{1},\,0),\,(b^{2},\,0),\, \ldots ,\, (b^{n},\,0),\,(0,\, x))=\psi (b^{1},\, \ldots ,\, b^{n},\,x)$![]() of this semi-direct product has to vanish and the multilinear consequence $\varphi$
of this semi-direct product has to vanish and the multilinear consequence $\varphi$![]() as well, which allows us to write $0= \sum \nolimits _{i=1} \lambda _i \varphi _i (b^{1} ,\, \ldots ,\, b^{i} x,\, \ldots ,\, b^{n})$
as well, which allows us to write $0= \sum \nolimits _{i=1} \lambda _i \varphi _i (b^{1} ,\, \ldots ,\, b^{i} x,\, \ldots ,\, b^{n})$![]() . Again, by construction of the actions, the elements $\varphi _i (b^{1} ,\, \ldots ,\, b^{i} x,\, \ldots ,\, b^{n})$
. Again, by construction of the actions, the elements $\varphi _i (b^{1} ,\, \ldots ,\, b^{i} x,\, \ldots ,\, b^{n})$![]() of $X$
of $X$![]() are linearly independent and thus $\lambda _i=0$
are linearly independent and thus $\lambda _i=0$![]() for all $i$
for all $i$![]() – which completes the proof.
– which completes the proof.
6 Conclusion and final remarks
We can now conclude with the main result of this article:
Theorem 6.1 Let ${\mathbb {K}}$![]() be an infinite field. Let ${\mathcal {V}}$
be an infinite field. Let ${\mathcal {V}}$![]() be a variety of non-associative algebras over ${\mathbb {K}}$
be a variety of non-associative algebras over ${\mathbb {K}}$![]() . If ${\mathcal {V}}$
. If ${\mathcal {V}}$![]() has representable representations – which happens, for instance, when it is action representable – then ${\mathcal {V}}$
has representable representations – which happens, for instance, when it is action representable – then ${\mathcal {V}}$![]() is either the variety of Lie algebras ${\mathsf {Lie}}_{\mathbb {K}}$
is either the variety of Lie algebras ${\mathsf {Lie}}_{\mathbb {K}}$![]() , the variety of quasi-Lie algebras ${\mathsf {qLie}}_{\mathbb {K}}$
, the variety of quasi-Lie algebras ${\mathsf {qLie}}_{\mathbb {K}}$![]() , or the category of vector spaces ${\mathsf {Vect}}_{{\mathbb {K}}}$
, or the category of vector spaces ${\mathsf {Vect}}_{{\mathbb {K}}}$![]() .
.
In [Reference García-Martínez and Van der Linden16], the first and third authors of the current article gave a different and a priori unrelated categorical description of Lie algebras, through a condition called local algebraic Cartesian closedness (LACC) introduced by J. R. A. Gray [Reference Gray19, Reference García-Martínez and Gray13, Reference Gray18]. Let us recall the main result:
Theorem 6.2 Let ${\mathbb {K}}$![]() be an infinite field and ${\mathcal {V}}$
be an infinite field and ${\mathcal {V}}$![]() a variety of $n$
a variety of $n$![]() -algebras over ${\mathbb {K}}$
-algebras over ${\mathbb {K}}$![]() which is a non-abelian locally algebraically Cartesian closed category. Then $n = 2$
which is a non-abelian locally algebraically Cartesian closed category. Then $n = 2$![]() and
and
(1) if ${\mathit {char}}({\mathbb {K}})\neq 2$
 , then ${\mathcal {V}} = {\mathsf {Lie}}_{{\mathbb {K}}} = {\mathsf {qLie}}_{{\mathbb {K}}}$
, then ${\mathcal {V}} = {\mathsf {Lie}}_{{\mathbb {K}}} = {\mathsf {qLie}}_{{\mathbb {K}}}$ ;
;(2) if ${\mathit {char}}({\mathbb {K}})= 2$
 , then ${\mathcal {V}} = {\mathsf {Lie}}_{{\mathbb {K}}}$
, then ${\mathcal {V}} = {\mathsf {Lie}}_{{\mathbb {K}}}$ or ${\mathcal {V}} = {\mathsf {qLie}}_{{\mathbb {K}}}$
or ${\mathcal {V}} = {\mathsf {qLie}}_{{\mathbb {K}}}$ .
.
This naturally leads to a number of questions which we hope to investigate in the future.
6.3 First question
Theorem 6.1 together with Theorem 6.2 tell us that, for non-associative algebras over an infinite field, action representability, representability of representations and (LACC) are equivalent conditions. On the other hand, for arbitrary semi-abelian categories, this is known to be false in general. Indeed, the category ${\mathsf {Bool}}$![]() of Boolean rings is action representable [Reference Borceux, Janelidze and Kelly4] but does not satisfy (LACC), as explained in Proposition 6.4 of [Reference Gray19]. Today it remains an open problem whether local algebraic Cartesian closedness implies action representability/representability of representations, or if some counterexample exists.
of Boolean rings is action representable [Reference Borceux, Janelidze and Kelly4] but does not satisfy (LACC), as explained in Proposition 6.4 of [Reference Gray19]. Today it remains an open problem whether local algebraic Cartesian closedness implies action representability/representability of representations, or if some counterexample exists.
Remark 6.4 We observe that ${\mathsf {Bool}}$![]() can be seen as the variety of non-associative ${\mathbb {Z}}_2$
can be seen as the variety of non-associative ${\mathbb {Z}}_2$![]() -algebras satisfying $xx=x$
-algebras satisfying $xx=x$![]() . The fact that this category is action representable emphasizes the necessity in Theorem 6.1 of working with an infinite field.
. The fact that this category is action representable emphasizes the necessity in Theorem 6.1 of working with an infinite field.
6.5 Second question
In order to obtain Theorem 6.2, the authors of [Reference García-Martínez and Van der Linden16] used a different inconsistent system of polynomial equations. Ours has 224 and may be reduced to a smaller system. Their system consists of 128 polynomials (and can in fact be further reduced as well). Whence, once again, a main result we were not able to prove without computer assistance. This makes us wonder whether a different proof technique exists, preferably a less computationally involved one.
6.6 Third question
What if instead of one multiplication, algebras have two? This is a natural question to ask, since Poisson algebras are an important example of this kind of object. Moreover, Poisson algebras over a fixed field form an Orzech category of interest, which simplifies the description of actions in this variety. The problem is that, for a given Poisson algebra $X$![]() , the Lie algebra ${\mathit {Der}}(X)$
, the Lie algebra ${\mathit {Der}}(X)$![]() of derivations on $X$
of derivations on $X$![]() need not form a Poisson algebra in general. Another potentially interesting example is the variety of Lie–Leibniz algebras introduced in [Reference Casas, Datuashvili and Ladra8].
need not form a Poisson algebra in general. Another potentially interesting example is the variety of Lie–Leibniz algebras introduced in [Reference Casas, Datuashvili and Ladra8].
Therefore, we may ask the following questions: ‘Are there action representable varieties of non-associative algebras with two multiplications? If not, can we prove this, and generalize the result to $n\geq 2$![]() multiplications?’ This might either result in a natural, categorical definition of ‘Lie algebras with two multiplications’, or in yet another uniqueness result for classical Lie algebras.
multiplications?’ This might either result in a natural, categorical definition of ‘Lie algebras with two multiplications’, or in yet another uniqueness result for classical Lie algebras.
6.7 Fourth question
What is the scope of representability of representations outside the context of algebras over a field? For instance, how far is it from action representability? What are examples of this condition, what are its consequences, does it admit any interesting characterizations?
Acknowledgements
We are grateful to the Institut de Recherche en Mathématique et Physique IRMP and the Department of Mathematics for their kind hospitality during our stays in Louvain-la-Neuve and in Santiago de Compostela.
The first author is a Postdoctoral Fellow of the Research Foundation–Flanders (FWO) and was supported by Ministerio de Economía y Competitividad (Spain), with grant number MTM2016-79661-P. The third author is a Research Associate of the Fonds de la Recherche Scientifique–FNRS. The fourth author is supported by the Fonds Thelam of the Fondation Roi Baudouin. Computational resources have been provided by the Consortium des Équipements de Calcul Intensif (CÉCI), funded by the Fonds de la Recherche Scientifique de Belgique (F.R.S.-FNRS) under Grant No. 2.5020.11 and by the Walloon Region.