Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-17T15:28:18.737Z Has data issue: false hasContentIssue false
  • English
  • Français

Baumslag–Solitar groups and residual nilpotence

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  16 June 2023

C.E. Kofinas ,
V. Metaftsis  and
A.I. Papistas
C.E. Kofinas
Affiliation:
Department of Mathematics, University of the Aegean, Karlovassi, Samos, Greece ([email protected]; [email protected])
V. Metaftsis
Affiliation:
Department of Mathematics, University of the Aegean, Karlovassi, Samos, Greece ([email protected]; [email protected])
A.I. Papistas
Affiliation:
Department of Mathematics, Aristotle University of Thessaloniki, Thessaloniki, Greece ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a Baumslag–Solitar group. We calculate the intersection 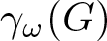$\gamma_{\omega}(G)$ of all terms of the lower central series of G. Using this, we show that 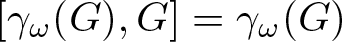$[\gamma_{\omega}(G),G]=\gamma_{\omega}(G)$, thus answering a question of Bardakov and Neschadim [1]. For any 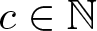$c \in \mathbb{N}$, with 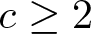$c \geq 2$, we show, by using Lie algebra methods, that the quotient group 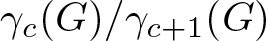$\gamma_{c}(G)/\gamma_{c+1}(G)$ of the lower central series of G is finite.

Keywords

Baumslag-Solitar groupsresidually nilpotentlower central seriesLie algebra

MSC classification

Primary: 20F14: Derived series, central series, and generalizations 20F40: Associated Lie structures 20F05: Generators, relations, and presentations 20E06: Free products, free products with amalgamation, Higman-Neumann-Neumann extensions, and generalizations 17B70: Graded Lie (super)algebras
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 2 , May 2023 , pp. 532 - 547
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bardakov, V. G. and Neshchadim, M. V., On the lower central series of Baumslag–Solitar groups, Algebra Logic 59 (2020), 281–294.10.1007/s10469-020-09601-zCrossRefGoogle Scholar
Baumslag, G. and Solitar, D., Some two-generator one-relator non-Hopfian groups, Bull. Amer. Math. Soc. 68 (1962), 199–201.10.1090/S0002-9904-1962-10745-9CrossRefGoogle Scholar
Bourbaki, N., Lie Groups and Lie Algebras Part I, Chapters 1–3 (Hermann, Paris, 1987).Google Scholar
Gruenberg, K. W., Residual properties of infinite soluble groups, Proc. Lond. Math. Soc. 7(3) (1957), 29–62.10.1112/plms/s3-7.1.29CrossRefGoogle Scholar
Kim, G. S. and McCarron, J., On amalgamated free products of residually p-finite groups, J. Algebra 162(1) (1993), 1–11.10.1006/jabr.1993.1237CrossRefGoogle Scholar
Lazard, M., Sur les groups nilpotents et les anneaux de Lie, Ann. Sci. Ec. Norm. Super. 71(3) (1954), 101–190.10.24033/asens.1021CrossRefGoogle Scholar
Levitt, G., Quotients and subgroups of Baumslag–Solitar groups, J. Group theory 18 (2015), 1–43.10.1515/jgth-2014-0028CrossRefGoogle Scholar
Meskin, S., Non-residually finite one-relator groups, Trans. Amer. Math. Soc. 164 (1972), 105–114.10.1090/S0002-9947-1972-0285589-5CrossRefGoogle Scholar
Moldavanskii, D. I., The intersection of the subgroups of finite p-index in Baumslag–Solitar groups, Vestnik Ivanovo State Univ. Ser. Natural Social Sci. 2 (2010), 106–111. (Russian).Google Scholar
Moldavanskii, D. I., The intersection of the subgroups of finite index in Baumslag–Solitar groups, Math. Notes 87(1) (2010), 88–95.10.1134/S0001434610010116CrossRefGoogle Scholar
Moldavanskii, D. I., On the residual properties of Baumslag–Solitar groups, Comm. Algebra 46(9) (2018), 3766–3778.10.1080/00927872.2018.1424867CrossRefGoogle Scholar
Raptis, E. and Varsos, D., Residual properties of HNN-extensions with base group an abelian group, J. Pure Appl. Algebra 59 (1989), 285–290.10.1016/0022-4049(89)90098-4CrossRefGoogle Scholar