Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-17T15:14:59.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomology in singular blocks of parabolic category 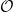$\mathcal{O}$

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  15 May 2023

Jonathan Gruber Open the ORCID record for Jonathan Gruber [Opens in a new window]
Jonathan Gruber*
Affiliation:
Department of Mathematics, National University of Singapore, Singapore, Singapore
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We determine the dimensions of 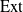$\textrm{Ext}$-groups between simple modules and dual generalized Verma modules in singular blocks of parabolic versions of category 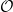$\mathcal{O}$ for complex semisimple Lie algebras and affine Kac-Moody algebras.

Keywords

cohomologyLie algebraKac-Moody algebraKoszul duality

MSC classification

Primary: 17B55: Homological methods in Lie (super)algebras 17B10: Representations, algebraic theory (weights)
Secondary: 17B67: Kac-Moody (super)algebras; extended affine Lie algebras; toroidal Lie algebras
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 65 , Issue 3 , September 2023 , pp. 555 - 568
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ágoston, I., Dlab, V. and Lukács, E., Quasi-hereditary extension algebras, Algebr. Represent. Theory 6(1) (2003), 97–117.Google Scholar
Backelin, E., Koszul duality for parabolic and singular category $\mathcal{O}$ , Represent. Theory 3 (1999), 139–152.Google Scholar
Beĭlinson, A. and Bernstein, J., Localisation de $g$ -modules, C. R. Acad. Sci. Paris Sér. I Math. 292(1) (1981), 15–18.Google Scholar
Beilinson, A., Ginzburg, V. and Soergel, W., Koszul duality patterns in representation theory, J. Amer. Math. Soc. 9(2) (1996), 473–527.Google Scholar
Brylinski, J.-L. and Kashiwara, M., Kazhdan-Lusztig conjecture and holonomic systems, Invent. Math. 64(3) (1981), 387–410.Google Scholar
Billey, S. C., Konvalinka, M., Petersen, T. K., Slofstra, W. and Tenner, B. E., Parabolic double cosets in Coxeter groups, Electron. J. Combin. 25(1) (2018), 66.Google Scholar
Bourbaki, N., Lie groups and Lie algebras, Chapters 4–6 (Springer, Cham, 2002).Google Scholar
Brundan, J. and Stroppel, C., Semi-infinite highest weight categories (2021). preprint. Available at https://arxiv.org/abs/1808.08022Google Scholar
Cline, E., Parshall, B. and Scott, L., Finite-dimensional algebras and highest weight categories, J. Reine Angew. Math. 391 (1988), 85–99.Google Scholar
Humphreys, J. E., Representations of semisimple Lie algebras in the BGG category O, Graduate Studies in Mathematics, vol. 94 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Jantzen, J. C., Moduln mit einem höchsten Gewicht, Lecture Notes in Mathematics, vol. 750 (Springer, Berlin, 1979).Google Scholar
Jantzen, J. C., Representations of algebraic groups, Mathematical Surveys and Monographs, vol. 107, 2nd edition (American Mathematical Society, Providence, RI, 2003).Google Scholar
Kazhdan, D. and Lusztig, G., Representations of Coxeter groups and Hecke algebras, Invent. Math. 53(2) (1979), 165–184.Google Scholar
Ko, H., Cohomology in singular blocks for a quantum group at a root of unity, Algebras Represent. Theory 22(5) (2019), 1109–1132.Google Scholar
Kashiwara, M. and Tanisaki, T., Kazhdan-Lusztig conjecture for affine Lie algebras with negative level, Duke Math. J. 77(1) (1995), 21–62.Google Scholar
Kashiwara, M. and Tanisaki, T., Characters of irreducible modules with non-critical highest weights over affine Lie algebras, in Representations and quantizations (Shanghai, 1998) (China High. Educ. Press, Beijing, 2000), 275–296.Google Scholar
Kumar, S., Kac-Moody groups, their flag varieties and representation theory, Progress in Mathematics, vol. 204 (Birkhäuser Boston, Inc., Boston, MA, 2002).CrossRefGoogle Scholar
Lanini, M., Ram, A. and Sobaje, P., A Fock space model for decomposition numbers for quantum groups at roots of unity, Kyoto J. Math. 59(4) (2019), 955–991.Google Scholar
Lusztig, G., On quantum groups, J. Algebra 131(2) (1990), 466–475.Google Scholar
Mazorchuk, V., Applications of the category of linear complexes of tilting modules associated with the category $\mathcal{O}$ , Algebr. Represent. Theory 12(6) (2009), 489–512.Google Scholar
Mazorchuk, V. and Ovsienko, S., A pairing in homology and the category of linear complexes of tilting modules for a quasi-hereditary algebra, J. Math. Kyoto Univ. 45(4) (2005), 711–741. With an appendix by Catharina Stroppel.Google Scholar
Rocha-Caridi, A. and Wallach, N. R., Projective modules over graded Lie algebras. I, Math. Z. 180(2) (1982), 151–177.Google Scholar
Soergel, W., $\mathfrak{n}$ -cohomology of simple highest weight modules on walls and purity, Invent. Math. 98(3) (1989), 565–580.Google Scholar
Soergel, W., Kazhdan-Lusztig-Polynome und eine Kombinatorik für Kipp-Moduln, Represent. Theory 1(4) (1997), 37–68.Google Scholar
Shan, P., Varagnolo, M. and Vasserot, E., Koszul duality of affine Kac-Moody algebras and cyclotomic rational double affine Hecke algebras, Adv. Math. 262 (2014), 370–435.Google Scholar
Tanisaki, T., Character formulas of Kazhdan-Lusztig type, in Representations of finite dimensional algebras and related topics in Lie theory and geometry, Fields Inst. Commun., vol. 40 (Amer. Math. Soc., Providence, RI, 2004), 261–276.Google Scholar
Vogan, D. A. Jr, Irreducible characters of semisimple Lie groups. II. The Kazhdan-Lusztig conjectures, Duke Math. J. 46(4) (1979), 805–859.Google Scholar