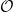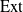1. Introduction
Let
![]() $\mathfrak{g}$
be a complex semisimple Lie algebra with Borel subalgebra
$\mathfrak{g}$
be a complex semisimple Lie algebra with Borel subalgebra
![]() $\mathfrak{b}$
and Cartan subalgebra
$\mathfrak{b}$
and Cartan subalgebra
![]() $\mathfrak{h} \subseteq \mathfrak{b}$
, and let
$\mathfrak{h} \subseteq \mathfrak{b}$
, and let
![]() $W \subseteq \textrm{GL}(\mathfrak{h}^*)$
be the Weyl group of
$W \subseteq \textrm{GL}(\mathfrak{h}^*)$
be the Weyl group of
![]() $\mathfrak{g}$
. For
$\mathfrak{g}$
. For
![]() $\lambda \in \mathfrak{h}^*$
, let us write
$\lambda \in \mathfrak{h}^*$
, let us write
![]() $\nabla _\lambda$
for the dual Verma module of highest weight
$\nabla _\lambda$
for the dual Verma module of highest weight
![]() $\lambda$
and
$\lambda$
and
![]() $L_\lambda$
for its unique simple submodule. The BGG category
$L_\lambda$
for its unique simple submodule. The BGG category
![]() $\mathcal{O}$
decomposes into blocks according to the dot action of
$\mathcal{O}$
decomposes into blocks according to the dot action of
![]() $W$
on
$W$
on
![]() $\mathfrak{h}^*$
given by
$\mathfrak{h}^*$
given by
![]() $w \boldsymbol{\cdot } \lambda = w(\lambda +\rho ) - \rho$
for
$w \boldsymbol{\cdot } \lambda = w(\lambda +\rho ) - \rho$
for
![]() $w \in W$
and
$w \in W$
and
![]() $\lambda \in \mathfrak{h}^*$
, where
$\lambda \in \mathfrak{h}^*$
, where
![]() $\rho$
denotes the half-sum of all positive roots of
$\rho$
denotes the half-sum of all positive roots of
![]() $\mathfrak{g}$
with respect to
$\mathfrak{g}$
with respect to
![]() $\mathfrak{b}$
. Let us write
$\mathfrak{b}$
. Let us write
![]() $\mathcal{O}_\lambda$
for the block corresponding to an integral and strictly anti-dominant weight
$\mathcal{O}_\lambda$
for the block corresponding to an integral and strictly anti-dominant weight
![]() $\lambda \in \mathfrak{h}^*$
. If
$\lambda \in \mathfrak{h}^*$
. If
![]() $\lambda$
is regular (i.e. if the stabilizer of
$\lambda$
is regular (i.e. if the stabilizer of
![]() $\lambda$
with respect to the dot action of
$\lambda$
with respect to the dot action of
![]() $W$
is trivial), then the composition multiplicities of simple modules in Verma modules in
$W$
is trivial), then the composition multiplicities of simple modules in Verma modules in
![]() $\mathcal{O}_\lambda$
can be computed as the values at
$\mathcal{O}_\lambda$
can be computed as the values at
![]() $1$
of certain Kazhdan-Lusztig polynomials. This result is known as the Kazhdan-Lusztig character formula; it was conjectured by D. Kazhdan and G. Lusztig in [Reference Kazhdan and Lusztig13] and proven by J.-L. Brylinski and M. Kashiwara in [Reference Brylinski and Kashiwara5] and by A. Beĭlinson and J. Bernstein in [Reference Beĭlinson and Bernstein3]. Even before the validity of the Kazhdan-Lusztig character formula had been established, it had been shown by D. Vogan in [Reference Vogan27] that its validity is equivalent to the formula
$1$
of certain Kazhdan-Lusztig polynomials. This result is known as the Kazhdan-Lusztig character formula; it was conjectured by D. Kazhdan and G. Lusztig in [Reference Kazhdan and Lusztig13] and proven by J.-L. Brylinski and M. Kashiwara in [Reference Brylinski and Kashiwara5] and by A. Beĭlinson and J. Bernstein in [Reference Beĭlinson and Bernstein3]. Even before the validity of the Kazhdan-Lusztig character formula had been established, it had been shown by D. Vogan in [Reference Vogan27] that its validity is equivalent to the formula
for all
![]() $x,y \in W$
, where
$x,y \in W$
, where
![]() $h_{y,x}$
denotes a Kazhdan-Lusztig polynomial (in the normalization of [Reference Soergel24]). In other words, the dimensions of
$h_{y,x}$
denotes a Kazhdan-Lusztig polynomial (in the normalization of [Reference Soergel24]). In other words, the dimensions of
![]() $\textrm{Ext}$
-groups between simple modules and dual Verma modules in
$\textrm{Ext}$
-groups between simple modules and dual Verma modules in
![]() $\mathcal{O}_\lambda$
are given by coefficients of Kazhdan-Lusztig polynomials. The formula (A) has been generalized by W. Soergel [Reference Soergel23] in two directions: Firstly, one can replace the regular weight
$\mathcal{O}_\lambda$
are given by coefficients of Kazhdan-Lusztig polynomials. The formula (A) has been generalized by W. Soergel [Reference Soergel23] in two directions: Firstly, one can replace the regular weight
![]() $\lambda$
by a singular weight (i.e. by a weight whose stabilizer with respect to the dot action of
$\lambda$
by a singular weight (i.e. by a weight whose stabilizer with respect to the dot action of
![]() $W$
is non-trivial), and secondly, one can replace the category
$W$
is non-trivial), and secondly, one can replace the category
![]() $\mathcal{O}_\lambda$
by its parabolic version
$\mathcal{O}_\lambda$
by its parabolic version
![]() $\mathcal{O}_\lambda ^{\mathfrak{p}}$
(and replace
$\mathcal{O}_\lambda ^{\mathfrak{p}}$
(and replace
![]() $\nabla _\lambda$
by a dual generalized Verma module
$\nabla _\lambda$
by a dual generalized Verma module
![]() $\nabla ^{\mathfrak{p}}_{\lambda }$
) for a parabolic subalgebra
$\nabla ^{\mathfrak{p}}_{\lambda }$
) for a parabolic subalgebra
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $\mathfrak{g}$
containing
$\mathfrak{g}$
containing
![]() $\mathfrak{b}$
. In both cases, the dimensions of
$\mathfrak{b}$
. In both cases, the dimensions of
![]() $\textrm{Ext}$
-groups between simple
$\textrm{Ext}$
-groups between simple
![]() $\mathfrak{g}$
-modules and dual (generalized) Verma modules are the coefficients of certain parabolic Kazhdan-Lusztig polynomials. In this note, we further generalize the formula (A) by considering blocks corresponding to singular weights in parabolic versions of
$\mathfrak{g}$
-modules and dual (generalized) Verma modules are the coefficients of certain parabolic Kazhdan-Lusztig polynomials. In this note, we further generalize the formula (A) by considering blocks corresponding to singular weights in parabolic versions of
![]() $\mathcal{O}$
. Our first main result is as follows; see Theorem 2.2. The notation is explained in Appendix A.
$\mathcal{O}$
. Our first main result is as follows; see Theorem 2.2. The notation is explained in Appendix A.
Theorem.
Let
![]() $\mu \in \mathfrak{h}^*$
be an integral strictly anti-dominant weight with stabilizer
$\mu \in \mathfrak{h}^*$
be an integral strictly anti-dominant weight with stabilizer
![]() $\textrm{Stab}_W(\mu ) = W_I = \langle I \rangle$
for some subset
$\textrm{Stab}_W(\mu ) = W_I = \langle I \rangle$
for some subset
![]() $I$
of the set of simple reflections in
$I$
of the set of simple reflections in
![]() $W$
, and let
$W$
, and let
![]() $\mathfrak{p} = \mathfrak{p}_J$
be a parabolic subalgebra of
$\mathfrak{p} = \mathfrak{p}_J$
be a parabolic subalgebra of
![]() $\mathfrak{g}$
containing
$\mathfrak{g}$
containing
![]() $\mathfrak{b}$
such that the Levi factor of
$\mathfrak{b}$
such that the Levi factor of
![]() $\mathfrak{p}$
has Weyl group
$\mathfrak{p}$
has Weyl group
![]() $W_J = \langle J \rangle$
for a subset
$W_J = \langle J \rangle$
for a subset
![]() $J$
of the set of simple reflections in
$J$
of the set of simple reflections in
![]() $W$
. Then we have
$W$
. Then we have
for all
![]() $x,y \in w_J{}^{J}{}{W}^I_{\textrm{reg}}$
, where
$x,y \in w_J{}^{J}{}{W}^I_{\textrm{reg}}$
, where
![]() $w_J$
denotes the longest element of
$w_J$
denotes the longest element of
![]() $W_J$
,
$W_J$
,
![]() ${}^{J}{}{W}^I_{\textrm{reg}}$
denotes the set of minimal length representatives for the regular double cosets in
${}^{J}{}{W}^I_{\textrm{reg}}$
denotes the set of minimal length representatives for the regular double cosets in
![]() $W_J \backslash W/ W_I$
, and
$W_J \backslash W/ W_I$
, and
![]() $n^I_{y^{-1},x^{-1}}$
denotes an anti-spherical Kazhdan-Lusztig polynomial.
$n^I_{y^{-1},x^{-1}}$
denotes an anti-spherical Kazhdan-Lusztig polynomial.
In Theorem 3.3, we establish an analogous result for singular blocks of parabolic category
![]() $\mathcal{O}$
for an affine Kac-Moody algebra. The strategy for proving these two theorems is the same: We first observe that the blocks of parabolic category
$\mathcal{O}$
for an affine Kac-Moody algebra. The strategy for proving these two theorems is the same: We first observe that the blocks of parabolic category
![]() $\mathcal{O}$
(or certain truncations thereof) admit standard Koszul gradings by the results of [Reference Backelin2] and [Reference Shan, Varagnolo and Vasserot25], so that the polynomials that record the dimensions of
$\mathcal{O}$
(or certain truncations thereof) admit standard Koszul gradings by the results of [Reference Backelin2] and [Reference Shan, Varagnolo and Vasserot25], so that the polynomials that record the dimensions of
![]() $\textrm{Ext}$
-groups (as in the theorem above) can be related to certain graded composition multiplicities. Then, we use graded analogues of translation functors in order to deduce our formulas from the known results about dimensions of
$\textrm{Ext}$
-groups (as in the theorem above) can be related to certain graded composition multiplicities. Then, we use graded analogues of translation functors in order to deduce our formulas from the known results about dimensions of
![]() $\textrm{Ext}$
-groups in regular blocks of parabolic category
$\textrm{Ext}$
-groups in regular blocks of parabolic category
![]() $\mathcal{O}$
. For affine Kac-Moody algebras, our proof also uses a “double parabolic inversion formula” for parabolic Kazhdan-Lusztig polynomials with respect to two different parabolic subgroups of a given Coxeter group, which we prove in Appendix A.
$\mathcal{O}$
. For affine Kac-Moody algebras, our proof also uses a “double parabolic inversion formula” for parabolic Kazhdan-Lusztig polynomials with respect to two different parabolic subgroups of a given Coxeter group, which we prove in Appendix A.
2. Gradings and Koszul duality
We first recall some well-known results about standard Koszul graded algebras and Koszul duality.
Let
![]() $\hat A = \bigoplus _{i \in \mathbb{Z}} A_i$
be a finite-dimensional graded algebra over a field
$\hat A = \bigoplus _{i \in \mathbb{Z}} A_i$
be a finite-dimensional graded algebra over a field
![]() $\Bbbk$
, with underlying (ungraded) algebra
$\Bbbk$
, with underlying (ungraded) algebra
![]() $A$
, and let
$A$
, and let
![]() $\mathcal{C}=A\text{-}\textrm{mod}$
and
$\mathcal{C}=A\text{-}\textrm{mod}$
and
![]() $\mathcal{C}_{\textrm{gr}} = \hat A\text{-}\textrm{grmod}$
be the categories of finite-dimensional left
$\mathcal{C}_{\textrm{gr}} = \hat A\text{-}\textrm{grmod}$
be the categories of finite-dimensional left
![]() $A$
-modules and of finite-dimensional graded left
$A$
-modules and of finite-dimensional graded left
![]() $\hat A$
-modules, respectively. In the following, we simply refer to the objects of
$\hat A$
-modules, respectively. In the following, we simply refer to the objects of
![]() $\mathcal{C}$
as
$\mathcal{C}$
as
![]() $A$
-modules and to the objects of
$A$
-modules and to the objects of
![]() $\mathcal{C}_{\textrm{gr}}$
as graded
$\mathcal{C}_{\textrm{gr}}$
as graded
![]() $\hat A$
-modules. A graded
$\hat A$
-modules. A graded
![]() $\hat A$
-module
$\hat A$
-module
![]() $M = \bigoplus _i M_i$
is called pure of degree
$M = \bigoplus _i M_i$
is called pure of degree
![]() $d \in \mathbb{Z}$
if
$d \in \mathbb{Z}$
if
![]() $M=M_d$
. For
$M=M_d$
. For
![]() $m \in \mathbb{Z}$
, let us further denote by
$m \in \mathbb{Z}$
, let us further denote by
![]() $\langle m \rangle \colon \mathcal{C}_{\textrm{gr}} \to \mathcal{C}_{\textrm{gr}}$
the
$\langle m \rangle \colon \mathcal{C}_{\textrm{gr}} \to \mathcal{C}_{\textrm{gr}}$
the
![]() $m$
-th grading shift functor, which sends a graded
$m$
-th grading shift functor, which sends a graded
![]() $\hat A$
-module
$\hat A$
-module
![]() $M = \bigoplus _i M_i$
to the graded
$M = \bigoplus _i M_i$
to the graded
![]() $\hat A$
-module
$\hat A$
-module
![]() $M\langle m \rangle = M$
, with the grading defined by
$M\langle m \rangle = M$
, with the grading defined by
![]() $M\langle m \rangle _i = M_{i-m}$
, and let
$M\langle m \rangle _i = M_{i-m}$
, and let
![]() $\textrm{f} \colon \mathcal{C}_{\textrm{gr}} \to \mathcal{C}$
be the functor that sends a graded
$\textrm{f} \colon \mathcal{C}_{\textrm{gr}} \to \mathcal{C}$
be the functor that sends a graded
![]() $\hat A$
-module to the underlying (ungraded)
$\hat A$
-module to the underlying (ungraded)
![]() $A$
-module. We call a graded
$A$
-module. We call a graded
![]() $\hat A$
-module
$\hat A$
-module
![]() $\tilde M$
a graded lift of an
$\tilde M$
a graded lift of an
![]() $A$
-module
$A$
-module
![]() $M$
if
$M$
if
![]() $M \cong \textrm{f}(\tilde M)$
. Now suppose additionally that
$M \cong \textrm{f}(\tilde M)$
. Now suppose additionally that
![]() $\hat A$
is positively graded, i.e. that
$\hat A$
is positively graded, i.e. that
![]() $A_i = 0$
for all
$A_i = 0$
for all
![]() $i\lt 0$
, and that
$i\lt 0$
, and that
![]() $A_0$
is a semisimple
$A_0$
is a semisimple
![]() $\Bbbk$
-algebra. Observe that
$\Bbbk$
-algebra. Observe that
![]() $A_{\gt i} = \bigoplus _{j\gt i} A_j$
is an ideal in
$A_{\gt i} = \bigoplus _{j\gt i} A_j$
is an ideal in
![]() $A$
for any
$A$
for any
![]() $i \geq 0$
and that we can consider
$i \geq 0$
and that we can consider
![]() $A_0$
as an
$A_0$
as an
![]() $A$
-module via the identification
$A$
-module via the identification
![]() $A_0 \cong A/ A_{\gt 0}$
.
$A_0 \cong A/ A_{\gt 0}$
.
Definition 1.1.
We say that
![]() $\hat A$
is Koszul if for all
$\hat A$
is Koszul if for all
![]() $i \in \mathbb{Z}_{\geq 0}$
and
$i \in \mathbb{Z}_{\geq 0}$
and
![]() $j \in \mathbb{Z}$
with
$j \in \mathbb{Z}$
with
![]() $i \neq j$
, we have
$i \neq j$
, we have
In that case, we also say that
![]() $A$
admits a Koszul grading.
$A$
admits a Koszul grading.
Consider the
![]() $\textrm{Ext}$
-algebra
$\textrm{Ext}$
-algebra
with the natural grading defined by
![]() $E(\hat A)_i = \textrm{Ext}_{\mathcal{C}}^i(A_0,A_0)$
for
$E(\hat A)_i = \textrm{Ext}_{\mathcal{C}}^i(A_0,A_0)$
for
![]() $i \in \mathbb{Z}$
. If
$i \in \mathbb{Z}$
. If
![]() $\hat A$
is Koszul then so is
$\hat A$
is Koszul then so is
![]() $E(\hat A)$
, and there is a canonical isomorphism of graded algebras
$E(\hat A)$
, and there is a canonical isomorphism of graded algebras
![]() $\hat A \cong E(E(\hat A))$
by Proposition 2.9.1 and Theorems 2.10.1 and 2.10.2 in [Reference Beilinson, Ginzburg and Soergel4]. When
$\hat A \cong E(E(\hat A))$
by Proposition 2.9.1 and Theorems 2.10.1 and 2.10.2 in [Reference Beilinson, Ginzburg and Soergel4]. When
![]() $\hat{A}$
is Koszul, we call the graded algebra
$\hat{A}$
is Koszul, we call the graded algebra
![]() $\hat A^! = E(\hat A)^{\textrm{op}}$
the Koszul dual of
$\hat A^! = E(\hat A)^{\textrm{op}}$
the Koszul dual of
![]() $\hat{A}$
; it is Koszul because the opposite algebra of a Koszul graded algebra is Koszul by Proposition 2.2.1 in [Reference Beilinson, Ginzburg and Soergel4]. We also write
$\hat{A}$
; it is Koszul because the opposite algebra of a Koszul graded algebra is Koszul by Proposition 2.2.1 in [Reference Beilinson, Ginzburg and Soergel4]. We also write
![]() $A^!$
for the underlying (ungraded) algebra of
$A^!$
for the underlying (ungraded) algebra of
![]() $\hat A^!$
.Footnote
1
Now additionally suppose that
$\hat A^!$
.Footnote
1
Now additionally suppose that
![]() $A$
has finite global dimension, so that
$A$
has finite global dimension, so that
![]() $E(A)$
is finite-dimensional. Then according to Theorems 2.12.5 and 2.12.6 in [Reference Beilinson, Ginzburg and Soergel4], there is an equivalence of triangulated categories
$E(A)$
is finite-dimensional. Then according to Theorems 2.12.5 and 2.12.6 in [Reference Beilinson, Ginzburg and Soergel4], there is an equivalence of triangulated categories
such that
![]() $K( M \langle i \rangle ) \cong K(M) \langle -i \rangle [{-}i ]$
for every graded
$K( M \langle i \rangle ) \cong K(M) \langle -i \rangle [{-}i ]$
for every graded
![]() $\hat A$
-module
$\hat A$
-module
![]() $M$
.
$M$
.
Now suppose that
![]() $\mathcal{C}$
is a highest weight category (see Definition 3.1 in [Reference Cline, Parshall and Scott9]) with finite weight poset
$\mathcal{C}$
is a highest weight category (see Definition 3.1 in [Reference Cline, Parshall and Scott9]) with finite weight poset
![]() $(\Lambda,\leq )$
and with simple objects
$(\Lambda,\leq )$
and with simple objects
![]() $L_\lambda$
, standard objects
$L_\lambda$
, standard objects
![]() $\Delta _\lambda$
and costandard objects
$\Delta _\lambda$
and costandard objects
![]() $\nabla _\lambda$
, for
$\nabla _\lambda$
, for
![]() $\lambda \in \Lambda$
. Let us further write
$\lambda \in \Lambda$
. Let us further write
![]() $I_\lambda$
and
$I_\lambda$
and
![]() $P_\lambda$
for the injective hull and the projective cover of
$P_\lambda$
for the injective hull and the projective cover of
![]() $L_\lambda$
, let
$L_\lambda$
, let
![]() $P = \bigoplus _{\lambda \in \Lambda } P_\lambda$
be a projective generator of
$P = \bigoplus _{\lambda \in \Lambda } P_\lambda$
be a projective generator of
![]() $\mathcal{C}$
and set
$\mathcal{C}$
and set
![]() $A\, :\!= \,\textrm{End}_{\mathcal{C}}(P)^{\textrm{op}}$
, so that
$A\, :\!= \,\textrm{End}_{\mathcal{C}}(P)^{\textrm{op}}$
, so that
![]() $\mathcal{C}$
is equivalent to
$\mathcal{C}$
is equivalent to
![]() $A\text{-}\textrm{mod}$
via the functor
$A\text{-}\textrm{mod}$
via the functor
![]() $\textrm{Hom}_{\mathcal{C}}(P,-)$
. In the following, we suppress the functor
$\textrm{Hom}_{\mathcal{C}}(P,-)$
. In the following, we suppress the functor
![]() $\textrm{Hom}_{\mathcal{C}}(P,-)$
from the notation and simply treat objects of
$\textrm{Hom}_{\mathcal{C}}(P,-)$
from the notation and simply treat objects of
![]() $\mathcal{C}$
as
$\mathcal{C}$
as
![]() $A$
-modules. From now on, additionally suppose that
$A$
-modules. From now on, additionally suppose that
![]() $A$
admits a positive grading
$A$
admits a positive grading
![]() $\hat{A} = \bigoplus _{i \in \mathbb{Z}} A_i$
such that
$\hat{A} = \bigoplus _{i \in \mathbb{Z}} A_i$
such that
![]() $A_0$
is a semisimple
$A_0$
is a semisimple
![]() $\Bbbk$
-algebra. Then, up to an isomorphism of graded
$\Bbbk$
-algebra. Then, up to an isomorphism of graded
![]() $\hat A$
-modules, any simple object
$\hat A$
-modules, any simple object
![]() $L_\lambda$
of highest weight
$L_\lambda$
of highest weight
![]() $\lambda \in \Lambda$
in
$\lambda \in \Lambda$
in
![]() $\mathcal{C}$
admits a unique graded lift
$\mathcal{C}$
admits a unique graded lift
![]() $\hat L_\lambda$
that is pure of degree
$\hat L_\lambda$
that is pure of degree
![]() $0$
, and the objects
$0$
, and the objects
![]() $\Delta _\lambda$
,
$\Delta _\lambda$
,
![]() $\nabla _\lambda$
,
$\nabla _\lambda$
,
![]() $P_\lambda$
, and
$P_\lambda$
, and
![]() $I_\lambda$
of
$I_\lambda$
of
![]() $\mathcal{C}$
admit unique graded lifts
$\mathcal{C}$
admit unique graded lifts
![]() $\hat \Delta _\lambda$
,
$\hat \Delta _\lambda$
,
![]() $\hat \nabla _\lambda$
,
$\hat \nabla _\lambda$
,
![]() $\hat P_\lambda$
and
$\hat P_\lambda$
and
![]() $\hat I_\lambda$
such that all non-zero homomorphisms
$\hat I_\lambda$
such that all non-zero homomorphisms
![]() $\Delta _\lambda \to L_\lambda$
,
$\Delta _\lambda \to L_\lambda$
,
![]() $L_\lambda \to \nabla _\lambda$
,
$L_\lambda \to \nabla _\lambda$
,
![]() $P_\lambda \to L_\lambda$
, and
$P_\lambda \to L_\lambda$
, and
![]() $L_\lambda \to I_\lambda$
are homomorphisms of graded
$L_\lambda \to I_\lambda$
are homomorphisms of graded
![]() $\hat A$
-modules. (See Corollary 4 and the introduction to Section 5 in [Reference Mazorchuk and Ovsienko21] for the existence and Lemma 2.5.1 in [Reference Beilinson, Ginzburg and Soergel4] for the uniqueness of these graded lifts.)
$\hat A$
-modules. (See Corollary 4 and the introduction to Section 5 in [Reference Mazorchuk and Ovsienko21] for the existence and Lemma 2.5.1 in [Reference Beilinson, Ginzburg and Soergel4] for the uniqueness of these graded lifts.)
Definition 1.2.
We say that
![]() $\hat A$
is standard Koszul if for all
$\hat A$
is standard Koszul if for all
![]() $\lambda,\mu \in \Lambda$
and all
$\lambda,\mu \in \Lambda$
and all
![]() $i \in \mathbb{Z}_{\geq 0}$
and
$i \in \mathbb{Z}_{\geq 0}$
and
![]() $j \in \mathbb{Z}$
with
$j \in \mathbb{Z}$
with
![]() $i \neq j$
, we have
$i \neq j$
, we have
In that case, we also say that
![]() $A$
admits a standard Koszul grading.
$A$
admits a standard Koszul grading.
If
![]() $\hat{A}$
is standard Koszul then
$\hat{A}$
is standard Koszul then
![]() $\hat{A}$
is Koszul,
$\hat{A}$
is Koszul,
![]() $\hat{A}^!$
is standard Koszul and the category
$\hat{A}^!$
is standard Koszul and the category
![]() $\mathcal{C}^! = A^!\text{-}\textrm{mod}$
is a highest weight category with weight poset
$\mathcal{C}^! = A^!\text{-}\textrm{mod}$
is a highest weight category with weight poset
![]() $(\Lambda,\leq ^{\textrm{op}})$
by Theorems 1, 2, and 3 in [Reference Ágoston, Dlab and Lukács1]. We denote the simple, standard, costandard, indecomposable projective, and indecomposable injective object of
$(\Lambda,\leq ^{\textrm{op}})$
by Theorems 1, 2, and 3 in [Reference Ágoston, Dlab and Lukács1]. We denote the simple, standard, costandard, indecomposable projective, and indecomposable injective object of
![]() $\mathcal{C}^!$
of highest weight
$\mathcal{C}^!$
of highest weight
![]() $\lambda \in \Lambda$
by
$\lambda \in \Lambda$
by
respectively, and we write
for their canonical graded lifts in the category
![]() $\mathcal{C}^!_{\textrm{gr}} =\hat A^!\text{-}\textrm{grmod}$
.
$\mathcal{C}^!_{\textrm{gr}} =\hat A^!\text{-}\textrm{grmod}$
.
Now we are ready to explain how Koszul duality can be used to relate dimensions of
![]() $\textrm{Ext}$
-groups with graded composition multiplicities. For
$\textrm{Ext}$
-groups with graded composition multiplicities. For
![]() $\nu,\lambda \in \Lambda$
, consider the polynomials
$\nu,\lambda \in \Lambda$
, consider the polynomials
Lemma 1.3.
Suppose that
![]() $\hat A$
is standard Koszul. Then,
$\hat A$
is standard Koszul. Then,
for all
![]() $\lambda,\mu \in \Lambda$
.
$\lambda,\mu \in \Lambda$
.
Proof. The proof is completely analogous to the proof of part (iii) of Theorem 3.11.4 in [Reference Beilinson, Ginzburg and Soergel4].
Now for
![]() $\nu,\lambda \in \Lambda$
, let us additionally consider the polynomials
$\nu,\lambda \in \Lambda$
, let us additionally consider the polynomials
Lemma 1.4.
Suppose that
![]() $\hat A$
is standard Koszul. Then,
$\hat A$
is standard Koszul. Then,
for all
![]() $\nu,\lambda \in \Lambda$
.
$\nu,\lambda \in \Lambda$
.
Proof. The proof is completely analogous to the proof of part (i) of Theorem 3.11.4 in [Reference Beilinson, Ginzburg and Soergel4], using the fact that the Koszul duality functor satisfies
for all
![]() $\lambda \in \Lambda$
by Proposition 2.7 in [Reference Ágoston, Dlab and Lukács1] and Theorem 2.12.5 in [Reference Beilinson, Ginzburg and Soergel4].
$\lambda \in \Lambda$
by Proposition 2.7 in [Reference Ágoston, Dlab and Lukács1] and Theorem 2.12.5 in [Reference Beilinson, Ginzburg and Soergel4].
3. Complex semisimple Lie algebras
Let
![]() $\mathfrak{g}$
be a complex semisimple Lie algebra with a Borel subalgebra
$\mathfrak{g}$
be a complex semisimple Lie algebra with a Borel subalgebra
![]() $\mathfrak{b}$
and a Cartan subalgebra
$\mathfrak{b}$
and a Cartan subalgebra
![]() $\mathfrak{h} \subseteq \mathfrak{b}$
, and let
$\mathfrak{h} \subseteq \mathfrak{b}$
, and let
![]() $\Phi \subseteq \mathfrak{h}^*$
be the root system of
$\Phi \subseteq \mathfrak{h}^*$
be the root system of
![]() $\mathfrak{g}$
with respect to
$\mathfrak{g}$
with respect to
![]() $\mathfrak{h}$
. We write
$\mathfrak{h}$
. We write
![]() $\Phi ^+ \subseteq \Phi$
for the positive system corresponding to
$\Phi ^+ \subseteq \Phi$
for the positive system corresponding to
![]() $\mathfrak{b}$
and let
$\mathfrak{b}$
and let
![]() $\Pi \subseteq \Phi ^+$
be a base of
$\Pi \subseteq \Phi ^+$
be a base of
![]() $\Phi$
. The Weyl group
$\Phi$
. The Weyl group
![]() $W = \langle s_\alpha \mid \alpha \in \Phi \rangle \subseteq \textrm{GL}(\mathfrak{h}^*)$
is a finite Coxeter group with simple reflections
$W = \langle s_\alpha \mid \alpha \in \Phi \rangle \subseteq \textrm{GL}(\mathfrak{h}^*)$
is a finite Coxeter group with simple reflections
![]() $S = \{ s_\alpha \mid \alpha \in \Pi \}$
, and we denote by
$S = \{ s_\alpha \mid \alpha \in \Pi \}$
, and we denote by
![]() $w_0$
the longest element of
$w_0$
the longest element of
![]() $W$
. We write
$W$
. We write
![]() $\alpha ^\vee \in \mathfrak{h}$
for the coroot of
$\alpha ^\vee \in \mathfrak{h}$
for the coroot of
![]() $\alpha \in \Phi$
and let
$\alpha \in \Phi$
and let
be the sets of integral weights and dominant weights, respectively. Furthermore, we write
![]() $\rho = \frac 12 \cdot \sum _{\alpha \in \Phi ^+} \alpha$
for the half-sum of all positive roots and consider the dot action of
$\rho = \frac 12 \cdot \sum _{\alpha \in \Phi ^+} \alpha$
for the half-sum of all positive roots and consider the dot action of
![]() $W$
on
$W$
on
![]() $\mathfrak{h}^*$
, which is defined by
$\mathfrak{h}^*$
, which is defined by
for
![]() $w \in W$
and
$w \in W$
and
![]() $\lambda \in \mathfrak{h}^*$
.
$\lambda \in \mathfrak{h}^*$
.
We consider the category
![]() $\mathcal{O}$
of finitely generated
$\mathcal{O}$
of finitely generated
![]() $\mathfrak{g}$
-modules that are locally
$\mathfrak{g}$
-modules that are locally
![]() $\mathfrak{b}$
-finite and admit a weight space decomposition with respect to
$\mathfrak{b}$
-finite and admit a weight space decomposition with respect to
![]() $\mathfrak{h}$
; see for instance [Reference Humphreys10]. For all
$\mathfrak{h}$
; see for instance [Reference Humphreys10]. For all
![]() $\lambda \in \mathfrak{h}^*$
, the Verma module
$\lambda \in \mathfrak{h}^*$
, the Verma module
![]() $\Delta _\lambda$
of highest weight
$\Delta _\lambda$
of highest weight
![]() $\lambda$
and its unique simple quotient
$\lambda$
and its unique simple quotient
![]() $L_\lambda$
are objects of
$L_\lambda$
are objects of
![]() $\mathcal{O}$
, and so is the dual Verma module
$\mathcal{O}$
, and so is the dual Verma module
![]() $\nabla _\lambda$
. For every weight
$\nabla _\lambda$
. For every weight
![]() $\lambda \in - \rho - X^+ = \{ - \rho - \lambda \mid \lambda \in X^+ \}$
, we denote by
$\lambda \in - \rho - X^+ = \{ - \rho - \lambda \mid \lambda \in X^+ \}$
, we denote by
![]() $\mathcal{O}_\lambda$
the block of
$\mathcal{O}_\lambda$
the block of
![]() $\mathcal{O}$
containing the simple
$\mathcal{O}$
containing the simple
![]() $\mathfrak{g}$
-module
$\mathfrak{g}$
-module
![]() $L_\lambda$
. The stabilizer of
$L_\lambda$
. The stabilizer of
![]() $\lambda$
with respect to the dot action of
$\lambda$
with respect to the dot action of
![]() $W$
on
$W$
on
![]() $\mathfrak{h}^*$
is a parabolic subgroup of
$\mathfrak{h}^*$
is a parabolic subgroup of
![]() $W$
, and for
$W$
, and for
![]() $I \subseteq S$
such that
$I \subseteq S$
such that
![]() $\textrm{Stab}_W(\lambda ) = W_I = \langle I \rangle$
, the isomorphism classes of simple
$\textrm{Stab}_W(\lambda ) = W_I = \langle I \rangle$
, the isomorphism classes of simple
![]() $\mathfrak{g}$
-modules in
$\mathfrak{g}$
-modules in
![]() $\mathcal{O}_\lambda$
are in bijection with the set
$\mathcal{O}_\lambda$
are in bijection with the set
![]() $W^I$
of elements
$W^I$
of elements
![]() $w \in W$
that have minimal length in the coset
$w \in W$
that have minimal length in the coset
![]() $w W_I$
(see Appendix A), via
$w W_I$
(see Appendix A), via
![]() $w \mapsto L_{w\boldsymbol{\cdot }\lambda }$
.
$w \mapsto L_{w\boldsymbol{\cdot }\lambda }$
.
Now let
![]() $J \subseteq S$
and denote by
$J \subseteq S$
and denote by
![]() $\mathfrak{p}_J$
the parabolic subalgebra of
$\mathfrak{p}_J$
the parabolic subalgebra of
![]() $\mathfrak{g}$
that is generated by
$\mathfrak{g}$
that is generated by
![]() $\mathfrak{b}$
together with the root spaces
$\mathfrak{b}$
together with the root spaces
![]() $\mathfrak{g}_{-\alpha }$
for
$\mathfrak{g}_{-\alpha }$
for
![]() $\alpha \in \Pi$
with
$\alpha \in \Pi$
with
![]() $s_\alpha \in J$
. We write
$s_\alpha \in J$
. We write
![]() $\mathcal{O}^{\mathfrak{p}_J}$
for the full subcategory of
$\mathcal{O}^{\mathfrak{p}_J}$
for the full subcategory of
![]() $\mathcal{O}$
whose objects are the locally
$\mathcal{O}$
whose objects are the locally
![]() $\mathfrak{p}_J$
-finite
$\mathfrak{p}_J$
-finite
![]() $\mathfrak{g}$
-modules in
$\mathfrak{g}$
-modules in
![]() $\mathcal{O}$
, and for
$\mathcal{O}$
, and for
![]() $\lambda \in -\rho - X^+$
, let
$\lambda \in -\rho - X^+$
, let
![]() $\mathcal{O}_\lambda ^{\mathfrak{p}_J}$
be the full subcategory of
$\mathcal{O}_\lambda ^{\mathfrak{p}_J}$
be the full subcategory of
![]() $\mathcal{O}_\lambda$
whose objects are the locally
$\mathcal{O}_\lambda$
whose objects are the locally
![]() $\mathfrak{p}_J$
-finite
$\mathfrak{p}_J$
-finite
![]() $\mathfrak{g}$
-modules in
$\mathfrak{g}$
-modules in
![]() $\mathcal{O}_\lambda$
. For
$\mathcal{O}_\lambda$
. For
![]() $I \subseteq S$
such that
$I \subseteq S$
such that
![]() $\textrm{Stab}_W(\lambda ) = W_I$
and for
$\textrm{Stab}_W(\lambda ) = W_I$
and for
![]() $w \in W^I$
, the simple
$w \in W^I$
, the simple
![]() $\mathfrak{g}$
-module
$\mathfrak{g}$
-module
![]() $L_{w\boldsymbol{\cdot }\lambda }$
belongs to
$L_{w\boldsymbol{\cdot }\lambda }$
belongs to
![]() $\mathcal{O}_\lambda ^{\mathfrak{p}_J}$
if and only if
$\mathcal{O}_\lambda ^{\mathfrak{p}_J}$
if and only if
![]() $(w\boldsymbol{\cdot }\lambda )(\alpha ^\vee ) \geq 0$
for all
$(w\boldsymbol{\cdot }\lambda )(\alpha ^\vee ) \geq 0$
for all
![]() $\alpha \in J$
, or equivalently, if
$\alpha \in J$
, or equivalently, if
![]() $w \in w_J{}^{J}{W} \cap W^I = w_J{}^{J}{W}^I_{\textrm{reg}}$
. Here, we write
$w \in w_J{}^{J}{W} \cap W^I = w_J{}^{J}{W}^I_{\textrm{reg}}$
. Here, we write
![]() $w_J$
for the longest element of
$w_J$
for the longest element of
![]() $W_J$
and
$W_J$
and
![]() ${}^{J}{W}$
for the set of elements
${}^{J}{W}$
for the set of elements
![]() $w \in W$
that have minimal length in the coset
$w \in W$
that have minimal length in the coset
![]() $W_J w$
, and we denote by
$W_J w$
, and we denote by
![]() ${}^{J}{W}^I_{\textrm{reg}}$
the set of minimal length representatives for the regular double cosets in
${}^{J}{W}^I_{\textrm{reg}}$
the set of minimal length representatives for the regular double cosets in
![]() $W_J \backslash W/ W_I$
(see Appendix A). In particular, the isomorphism classes of simple
$W_J \backslash W/ W_I$
(see Appendix A). In particular, the isomorphism classes of simple
![]() $\mathfrak{g}$
-modules in
$\mathfrak{g}$
-modules in
![]() $\mathcal{O}_\lambda ^{\mathfrak{p}_J}$
are in bijection with the set
$\mathcal{O}_\lambda ^{\mathfrak{p}_J}$
are in bijection with the set
![]() $w_J{}^{J}{W}^I_{\textrm{reg}}$
via
$w_J{}^{J}{W}^I_{\textrm{reg}}$
via
![]() $w \mapsto L_{w\boldsymbol{\cdot }\lambda }$
. For
$w \mapsto L_{w\boldsymbol{\cdot }\lambda }$
. For
![]() $\mu \in \mathfrak{h}^*$
, let us write
$\mu \in \mathfrak{h}^*$
, let us write
![]() $\Delta ^{\mathfrak{p}_J}_\mu$
for the largest quotient of
$\Delta ^{\mathfrak{p}_J}_\mu$
for the largest quotient of
![]() $\Delta _\mu$
that belongs to
$\Delta _\mu$
that belongs to
![]() $\mathcal{O}^{\mathfrak{p}_J}$
and
$\mathcal{O}^{\mathfrak{p}_J}$
and
![]() $\nabla ^{\mathfrak{p}_J}_\mu$
for the largest submodule of
$\nabla ^{\mathfrak{p}_J}_\mu$
for the largest submodule of
![]() $\nabla _\mu$
that belongs to
$\nabla _\mu$
that belongs to
![]() $\mathcal{O}^{\mathfrak{p}_J}$
and call these
$\mathcal{O}^{\mathfrak{p}_J}$
and call these
![]() $\mathfrak{g}$
-modules the generalized or parabolic Verma module and dual Verma module, respectively, of highest weight
$\mathfrak{g}$
-modules the generalized or parabolic Verma module and dual Verma module, respectively, of highest weight
![]() $\mu$
with respect to
$\mu$
with respect to
![]() $\mathfrak{p}_J$
. Then,
$\mathfrak{p}_J$
. Then,
![]() $\mathcal{O}_\lambda ^{\mathfrak{p}_J}$
is a highest weight category with weight poset
$\mathcal{O}_\lambda ^{\mathfrak{p}_J}$
is a highest weight category with weight poset
![]() $(w_J{}^{J}{W}^I_{\textrm{reg}},\leq )$
, where
$(w_J{}^{J}{W}^I_{\textrm{reg}},\leq )$
, where
![]() $\leq$
denotes the Bruhat order, with simple objects
$\leq$
denotes the Bruhat order, with simple objects
![]() $L_{w\boldsymbol{\cdot }\lambda }$
, standard objects
$L_{w\boldsymbol{\cdot }\lambda }$
, standard objects
![]() $\Delta ^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
, and costandard objects
$\Delta ^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
, and costandard objects
![]() $\nabla ^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
for
$\nabla ^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
for
![]() $w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
. Let us further write
$w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
. Let us further write
![]() $P^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
for the projective cover of
$P^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
for the projective cover of
![]() $L_{w\boldsymbol{\cdot }\lambda }$
in
$L_{w\boldsymbol{\cdot }\lambda }$
in
![]() $\mathcal{O}^{\mathfrak{p}_J}_\lambda$
, for
$\mathcal{O}^{\mathfrak{p}_J}_\lambda$
, for
![]() $w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
. We define
$w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
. We define
so that
![]() $\mathcal{O}^{\mathfrak{p}_J}_\lambda$
is equivalent to the category
$\mathcal{O}^{\mathfrak{p}_J}_\lambda$
is equivalent to the category
![]() $A^{\mathfrak{p}_J}_\lambda \text{-}\textrm{mod}$
. The following theorem combines the results of E. Backelin and V. Mazorchuk; it will be crucial for our determination of the dimensions of
$A^{\mathfrak{p}_J}_\lambda \text{-}\textrm{mod}$
. The following theorem combines the results of E. Backelin and V. Mazorchuk; it will be crucial for our determination of the dimensions of
![]() $\textrm{Ext}$
-groups between simple objects and costandard objects in
$\textrm{Ext}$
-groups between simple objects and costandard objects in
![]() $\mathcal{O}^{\mathfrak{p}_J}_\lambda$
.
$\mathcal{O}^{\mathfrak{p}_J}_\lambda$
.
Theorem 2.1.
Let
![]() $\lambda,\mu \in - \rho - X^+$
and let
$\lambda,\mu \in - \rho - X^+$
and let
![]() $I,J \subseteq S$
such that
$I,J \subseteq S$
such that
![]() $\textrm{Stab}_W(\lambda ) = W_I$
and
$\textrm{Stab}_W(\lambda ) = W_I$
and
![]() $\textrm{Stab}_W(\mu ) = W_J$
. Then, the algebra
$\textrm{Stab}_W(\mu ) = W_J$
. Then, the algebra
![]() $A_\lambda ^{\mathfrak{p}_J}$
admits a standard Koszul grading, and its Koszul dual
$A_\lambda ^{\mathfrak{p}_J}$
admits a standard Koszul grading, and its Koszul dual
![]() $(A_\lambda ^{\mathfrak{p}_J})^!$
is isomorphic to the algebra
$(A_\lambda ^{\mathfrak{p}_J})^!$
is isomorphic to the algebra
![]() $A_{-w_0\mu }^{\mathfrak{p}_I}$
.
$A_{-w_0\mu }^{\mathfrak{p}_I}$
.
Proof. By Theorem 1.1 in [Reference Backelin2], the algebra
![]() $A_\lambda ^{\mathfrak{p}_J}$
admits a Koszul grading and its Koszul dual
$A_\lambda ^{\mathfrak{p}_J}$
admits a Koszul grading and its Koszul dual
![]() $(A_\lambda ^{\mathfrak{p}_J})^!$
is isomorphic to the algebra
$(A_\lambda ^{\mathfrak{p}_J})^!$
is isomorphic to the algebra
![]() $A_{-w_0\mu }^{\mathfrak{p}_I}$
. The standard Koszulity of the Koszul graded version of
$A_{-w_0\mu }^{\mathfrak{p}_I}$
. The standard Koszulity of the Koszul graded version of
![]() $A_\lambda ^{\mathfrak{p}_J}$
is established in Theorem 5.1 of [Reference Mazorchuk20].
$A_\lambda ^{\mathfrak{p}_J}$
is established in Theorem 5.1 of [Reference Mazorchuk20].
We keep the notation and assumptions of Theorem 2.1 and define
For
![]() $w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
, we further write
$w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
, we further write
![]() $e^{\mathfrak{p}_J}_{\lambda,w}$
for the idempotent in
$e^{\mathfrak{p}_J}_{\lambda,w}$
for the idempotent in
![]() $A^{\mathfrak{p}_J}_\lambda$
corresponding to the canonical projection
$A^{\mathfrak{p}_J}_\lambda$
corresponding to the canonical projection
![]() $\textrm{P}^{\mathfrak{p}_J}_\lambda \to P^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
and
$\textrm{P}^{\mathfrak{p}_J}_\lambda \to P^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
and
![]() $f^{\mathfrak{p}_J}_{\lambda,w}$
for the idempotent in the Koszul dual
$f^{\mathfrak{p}_J}_{\lambda,w}$
for the idempotent in the Koszul dual
![]() $( A^{\mathfrak{p}_J}_\lambda )^!$
corresponding to the canonical projection
$( A^{\mathfrak{p}_J}_\lambda )^!$
corresponding to the canonical projection
![]() $\textrm{L}^{\mathfrak{p}_J}_\lambda \to L_{w\boldsymbol{\cdot }\lambda }$
. Then, according to Remark 3.8 (and Proposition 3.1) in [Reference Backelin2], the isomorphism
$\textrm{L}^{\mathfrak{p}_J}_\lambda \to L_{w\boldsymbol{\cdot }\lambda }$
. Then, according to Remark 3.8 (and Proposition 3.1) in [Reference Backelin2], the isomorphism
from Theorem 2.1 can be chosen in such a way that
for all
![]() $w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
.Footnote
2
In particular, if we write
$w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
.Footnote
2
In particular, if we write
![]() $L^{\mathfrak{p}_J,!}_{\lambda,w}$
for the simple
$L^{\mathfrak{p}_J,!}_{\lambda,w}$
for the simple
![]() $( A^{\mathfrak{p}_J}_\lambda )^!$
-module corresponding to an element
$( A^{\mathfrak{p}_J}_\lambda )^!$
-module corresponding to an element
![]() $w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
(as described in Section 1), then the functor
$w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
(as described in Section 1), then the functor
induced by
![]() $\varphi ^{-1}$
sends the simple
$\varphi ^{-1}$
sends the simple
![]() $( A^{\mathfrak{p}_J}_\lambda )^!$
-module
$( A^{\mathfrak{p}_J}_\lambda )^!$
-module
![]() $L^{\mathfrak{p}_J,!}_{\lambda,w}$
to the simple
$L^{\mathfrak{p}_J,!}_{\lambda,w}$
to the simple
![]() $\mathfrak{g}$
-module
$\mathfrak{g}$
-module
![]() $L_{w^{-1} w_0\boldsymbol{\cdot }({-}w_0\mu )}$
.
$L_{w^{-1} w_0\boldsymbol{\cdot }({-}w_0\mu )}$
.
Now for a subset
![]() $I \subseteq S$
and
$I \subseteq S$
and
![]() $x,y \in{}^{I}{W}$
, let us denote by
$x,y \in{}^{I}{W}$
, let us denote by
![]() $m^I_{x,y}$
,
$m^I_{x,y}$
,
![]() $m_I^{x,y}$
,
$m_I^{x,y}$
,
![]() $n^I_{x,y}$
, and
$n^I_{x,y}$
, and
![]() $n_I^{x,y}$
the corresponding spherical and anti-spherical (inverse) parabolic Kazhdan-Lusztig polynomials, as defined in Appendix A. With all of the above notation in place, we can prove the first main result.
$n_I^{x,y}$
the corresponding spherical and anti-spherical (inverse) parabolic Kazhdan-Lusztig polynomials, as defined in Appendix A. With all of the above notation in place, we can prove the first main result.
Theorem 2.2.
Let
![]() $\lambda,\mu \in - \rho - X^+$
and let
$\lambda,\mu \in - \rho - X^+$
and let
![]() $I,J \subseteq S$
such that
$I,J \subseteq S$
such that
![]() $\textrm{Stab}_W(\lambda ) = W_I$
and
$\textrm{Stab}_W(\lambda ) = W_I$
and
![]() $\textrm{Stab}_W(\mu ) = W_J$
. For
$\textrm{Stab}_W(\mu ) = W_J$
. For
![]() $x,z \in w_J{}^{J}{}{W}^I_{\textrm{reg}}$
, we have
$x,z \in w_J{}^{J}{}{W}^I_{\textrm{reg}}$
, we have
Proof. For
![]() $w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
, let us write
$w \in w_J{}^{J}{W}^I_{\textrm{reg}}$
, let us write
![]() $\hat L^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
and
$\hat L^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
and
![]() $\hat \Delta ^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
for the canonical graded lifts of
$\hat \Delta ^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
for the canonical graded lifts of
![]() $L_{w\boldsymbol{\cdot }\lambda }$
and
$L_{w\boldsymbol{\cdot }\lambda }$
and
![]() $\Delta ^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
, respectively, in the category of graded modules over a Koszul graded version of
$\Delta ^{\mathfrak{p}_J}_{w\boldsymbol{\cdot }\lambda }$
, respectively, in the category of graded modules over a Koszul graded version of
![]() $A^{\mathfrak{p}_J}_\lambda$
. Then, according to Lemma 1.4 and the above discussion of Koszul duality for
$A^{\mathfrak{p}_J}_\lambda$
. Then, according to Lemma 1.4 and the above discussion of Koszul duality for
![]() $\mathcal{O}^{\mathfrak{p}_J}_\lambda$
, the polynomials
$\mathcal{O}^{\mathfrak{p}_J}_\lambda$
, the polynomials
with
![]() $x,y,z \in w_J{}^{J}{W}^I_{\textrm{reg}}$
are related via the equations
$x,y,z \in w_J{}^{J}{W}^I_{\textrm{reg}}$
are related via the equations
We first consider a special case of the formula in the theorem, which we will then use to prove the general statement: For
![]() $\lambda ^\prime \in - \rho - X^+$
with
$\lambda ^\prime \in - \rho - X^+$
with
![]() $\textrm{Stab}_W(\lambda ^\prime ) = \{ e \}$
, we have
$\textrm{Stab}_W(\lambda ^\prime ) = \{ e \}$
, we have
for all
![]() $y,z \in w_J{}^{J}{W}$
by parts (i) and (iv) of Theorem 3.11.4 in [Reference Beilinson, Ginzburg and Soergel4]. Now let
$y,z \in w_J{}^{J}{W}$
by parts (i) and (iv) of Theorem 3.11.4 in [Reference Beilinson, Ginzburg and Soergel4]. Now let
![]() $\hat A^{\mathfrak{p}_J}_\lambda$
and
$\hat A^{\mathfrak{p}_J}_\lambda$
and
![]() $\hat A^{\mathfrak{p}_J}_{\lambda ^\prime }$
be Koszul graded algebras whose underlying ungraded algebras are
$\hat A^{\mathfrak{p}_J}_{\lambda ^\prime }$
be Koszul graded algebras whose underlying ungraded algebras are
![]() $A^{\mathfrak{p}_J}_\lambda$
and
$A^{\mathfrak{p}_J}_\lambda$
and
![]() $A^{\mathfrak{p}_J}_{\lambda ^\prime }$
, respectively, and let
$A^{\mathfrak{p}_J}_{\lambda ^\prime }$
, respectively, and let
be the corresponding categories of graded modules. For
![]() $J=\varnothing$
, we omit the superscript
$J=\varnothing$
, we omit the superscript
![]() $\mathfrak{p}_J$
and write
$\mathfrak{p}_J$
and write
Then, by the proof of Proposition 3.2 in [Reference Backelin2], the graded algebra
![]() $\hat A^{\mathfrak{p}_J}_\lambda$
is the quotient of
$\hat A^{\mathfrak{p}_J}_\lambda$
is the quotient of
![]() $\hat A_\lambda$
by some homogeneous ideal, whence we can consider
$\hat A_\lambda$
by some homogeneous ideal, whence we can consider
![]() $\mathcal{O}^{\mathfrak{p}_J}_{\lambda,\textrm{gr}}$
as a full subcategory of
$\mathcal{O}^{\mathfrak{p}_J}_{\lambda,\textrm{gr}}$
as a full subcategory of
![]() $\mathcal{O}_{\lambda,\textrm{gr}}$
, and similarly for
$\mathcal{O}_{\lambda,\textrm{gr}}$
, and similarly for
![]() $\mathcal{O}^{\mathfrak{p}_J}_{\lambda ^\prime,\textrm{gr}}$
and
$\mathcal{O}^{\mathfrak{p}_J}_{\lambda ^\prime,\textrm{gr}}$
and
![]() $\mathcal{O}_{\lambda ^\prime,\textrm{gr}}$
. (See also Lemma 2.2 in [Reference Shan, Varagnolo and Vasserot25] and Theorem 3.5.3 in [Reference Beilinson, Ginzburg and Soergel4].) Furthermore, as shown in part (d) of the proof of Lemma 3.3 in [Reference Backelin2], there is an exact functor
$\mathcal{O}_{\lambda ^\prime,\textrm{gr}}$
. (See also Lemma 2.2 in [Reference Shan, Varagnolo and Vasserot25] and Theorem 3.5.3 in [Reference Beilinson, Ginzburg and Soergel4].) Furthermore, as shown in part (d) of the proof of Lemma 3.3 in [Reference Backelin2], there is an exact functor
which lifts the usual translation functor
![]() $T_{\lambda ^\prime }^\lambda \colon \mathcal{O}_{\lambda ^\prime } \to \mathcal{O}_\lambda$
and sends any pure object in
$T_{\lambda ^\prime }^\lambda \colon \mathcal{O}_{\lambda ^\prime } \to \mathcal{O}_\lambda$
and sends any pure object in
![]() $\mathcal{O}_{\lambda ^\prime,\textrm{gr}}$
to a pure object of the same degree in
$\mathcal{O}_{\lambda ^\prime,\textrm{gr}}$
to a pure object of the same degree in
![]() $\mathcal{O}_{\lambda,\textrm{gr}}$
. Using well-known properties of translation functors (see Section 7.9 in [Reference Humphreys10]), it follows that
$\mathcal{O}_{\lambda,\textrm{gr}}$
. Using well-known properties of translation functors (see Section 7.9 in [Reference Humphreys10]), it follows that
 \begin{equation*} \hat T_{\lambda ^\prime }^\lambda \hat L_{y\boldsymbol {\cdot }\lambda ^\prime } \cong \begin {cases} \hat L_{y\boldsymbol {\cdot }\lambda } & \text {if } y \in W^I, \\ 0 & \text {otherwise} \end {cases} \end{equation*}
\begin{equation*} \hat T_{\lambda ^\prime }^\lambda \hat L_{y\boldsymbol {\cdot }\lambda ^\prime } \cong \begin {cases} \hat L_{y\boldsymbol {\cdot }\lambda } & \text {if } y \in W^I, \\ 0 & \text {otherwise} \end {cases} \end{equation*}
for all
![]() $y \in W$
and that
$y \in W$
and that
![]() $\hat T_{\lambda ^\prime }^\lambda$
restricts to a functor from
$\hat T_{\lambda ^\prime }^\lambda$
restricts to a functor from
![]() $\mathcal{O}^{\mathfrak{p}_J}_{\lambda ^\prime,\textrm{gr}}$
to
$\mathcal{O}^{\mathfrak{p}_J}_{\lambda ^\prime,\textrm{gr}}$
to
![]() $\mathcal{O}^{\mathfrak{p}_J}_{\lambda,\textrm{gr}}$
with
$\mathcal{O}^{\mathfrak{p}_J}_{\lambda,\textrm{gr}}$
with
for all
![]() $z \in w_J{}^{J}{W}^I_{\textrm{reg}}$
.Footnote
3
Now the exactness of
$z \in w_J{}^{J}{W}^I_{\textrm{reg}}$
.Footnote
3
Now the exactness of
![]() $\hat T_{\lambda ^\prime }^\lambda$
implies that
$\hat T_{\lambda ^\prime }^\lambda$
implies that
for all
![]() $y,z \in w_J{}^{J}{W}^I_{\textrm{reg}}$
and all
$y,z \in w_J{}^{J}{W}^I_{\textrm{reg}}$
and all
![]() $i \in \mathbb{Z}$
. In particular, the special case at the beginning of the proof implies that
$i \in \mathbb{Z}$
. In particular, the special case at the beginning of the proof implies that
![]() $q^{\mathfrak{p}_J}_{\lambda,z,y} = q^{\mathfrak{p}_J}_{\lambda ^\prime,z,y} = n^J_{zw_0,yw_0}$
for all
$q^{\mathfrak{p}_J}_{\lambda,z,y} = q^{\mathfrak{p}_J}_{\lambda ^\prime,z,y} = n^J_{zw_0,yw_0}$
for all
![]() $y,z \in w_J{}^{J}{W}^I_{\textrm{reg}}$
, and using (2.1), we obtain
$y,z \in w_J{}^{J}{W}^I_{\textrm{reg}}$
, and using (2.1), we obtain
for all
![]() $x,z \in w_J{}^{J}{W}^I_{\textrm{reg}}$
, as required.
$x,z \in w_J{}^{J}{W}^I_{\textrm{reg}}$
, as required.
4. Affine Kac-Moody algebras
Let us keep the notation from the previous section and additionally assume that
![]() $\mathfrak{g}$
is a complex simple Lie algebra. Recall that we fix a Borel subalgebra
$\mathfrak{g}$
is a complex simple Lie algebra. Recall that we fix a Borel subalgebra
![]() $\mathfrak{b}$
and a Cartan subalgebra
$\mathfrak{b}$
and a Cartan subalgebra
![]() $\mathfrak{h} \subseteq \mathfrak{b}$
of
$\mathfrak{h} \subseteq \mathfrak{b}$
of
![]() $\mathfrak{g}$
. We consider the affine Kac-Moody Lie algebra
$\mathfrak{g}$
. We consider the affine Kac-Moody Lie algebra
as in [Reference Tanisaki26, Section 6] and its subalgebras
and we view
![]() $\mathfrak{h}^*$
as a subspace of
$\mathfrak{h}^*$
as a subspace of
![]() $\mathfrak{\tilde h}^*$
, with the convention that
$\mathfrak{\tilde h}^*$
, with the convention that
![]() $\lambda (c) = \lambda (d) = 0$
for all
$\lambda (c) = \lambda (d) = 0$
for all
![]() $\lambda \in \mathfrak{h}^*$
. Let
$\lambda \in \mathfrak{h}^*$
. Let
![]() $\tilde \Phi$
be the root system of
$\tilde \Phi$
be the root system of
![]() $\mathfrak{\tilde g}$
and let
$\mathfrak{\tilde g}$
and let
![]() $\tilde \Phi ^+$
be the set of positive roots corresponding to
$\tilde \Phi ^+$
be the set of positive roots corresponding to
![]() $\mathfrak{\tilde b}$
, again as in [Reference Tanisaki26, Section 6]. Further, let
$\mathfrak{\tilde b}$
, again as in [Reference Tanisaki26, Section 6]. Further, let
![]() $\tilde \Pi = \Pi \sqcup \{ \alpha _0 \}$
be the set of simple roots in
$\tilde \Pi = \Pi \sqcup \{ \alpha _0 \}$
be the set of simple roots in
![]() $\tilde \Phi$
and let
$\tilde \Phi$
and let
be the (affine) Weyl group of
![]() $\mathfrak{\tilde g}$
. It is a Coxeter group with set of simple reflections
$\mathfrak{\tilde g}$
. It is a Coxeter group with set of simple reflections
![]() $\tilde S = \{ s_\alpha \mid \alpha \in \tilde \Pi \}$
, and it is canonically isomorphic to the semidirect product
$\tilde S = \{ s_\alpha \mid \alpha \in \tilde \Pi \}$
, and it is canonically isomorphic to the semidirect product
![]() $W \rtimes \mathbb{Z}\Phi ^\vee$
, where
$W \rtimes \mathbb{Z}\Phi ^\vee$
, where
![]() $W$
denotes the Weyl group of
$W$
denotes the Weyl group of
![]() $\mathfrak{g}$
and
$\mathfrak{g}$
and
![]() $\mathbb{Z}\Phi ^\vee$
is the coroot lattice of
$\mathbb{Z}\Phi ^\vee$
is the coroot lattice of
![]() $\mathfrak{g}$
(see Proposition 13.1.7 in [Reference Kumar17]). Let us write
$\mathfrak{g}$
(see Proposition 13.1.7 in [Reference Kumar17]). Let us write
![]() $\alpha ^\vee \in \mathfrak{\tilde h}$
for the coroot corresponding to
$\alpha ^\vee \in \mathfrak{\tilde h}$
for the coroot corresponding to
![]() $\alpha \in \tilde \Pi$
and define
$\alpha \in \tilde \Pi$
and define
![]() $\tilde \rho \in \mathfrak{\tilde h}^*$
by
$\tilde \rho \in \mathfrak{\tilde h}^*$
by
![]() $\tilde \rho (\alpha ^\vee ) = 1$
for all
$\tilde \rho (\alpha ^\vee ) = 1$
for all
![]() $\alpha \in \tilde \Pi$
and
$\alpha \in \tilde \Pi$
and
![]() $\tilde \rho (d) = 0$
. The dot action of
$\tilde \rho (d) = 0$
. The dot action of
![]() $\tilde W$
on
$\tilde W$
on
![]() $\mathfrak{\tilde h}^*$
is given by
$\mathfrak{\tilde h}^*$
is given by
for all
![]() $w \in \tilde W$
and
$w \in \tilde W$
and
![]() $\lambda \in \mathfrak{\tilde h}^*$
. We say that
$\lambda \in \mathfrak{\tilde h}^*$
. We say that
![]() $\lambda \in \mathfrak{\tilde h}^*$
has level
$\lambda \in \mathfrak{\tilde h}^*$
has level
![]() $e \in \mathbb{C}$
if
$e \in \mathbb{C}$
if
![]() $e = ( \lambda + \tilde \rho )(c)$
, and we set
$e = ( \lambda + \tilde \rho )(c)$
, and we set
so that
![]() $\lambda ^\prime$
has level
$\lambda ^\prime$
has level
![]() $-e$
when
$-e$
when
![]() $\lambda$
has level
$\lambda$
has level
![]() $e$
and
$e$
and
![]() $(w \boldsymbol{\cdot } \lambda )^\prime = w\boldsymbol{\cdot }\lambda ^\prime$
for all
$(w \boldsymbol{\cdot } \lambda )^\prime = w\boldsymbol{\cdot }\lambda ^\prime$
for all
![]() $w \in \tilde W$
. The sets of integral and dominant weights are defined by
$w \in \tilde W$
. The sets of integral and dominant weights are defined by
respectively, and we note that for every integral weight
![]() $\mu \in \tilde X$
of positive (or negative) level, there is a unique weight
$\mu \in \tilde X$
of positive (or negative) level, there is a unique weight
![]() $\nu \in \tilde X^+ \setminus \{0\}$
such that
$\nu \in \tilde X^+ \setminus \{0\}$
such that
![]() $\mu$
belongs to the
$\mu$
belongs to the
![]() $\tilde W$
-orbit of
$\tilde W$
-orbit of
![]() $\nu - \tilde \rho$
(respectively
$\nu - \tilde \rho$
(respectively
![]() $-\nu - \tilde \rho$
) with respect to the dot action; see for instance Section 6.3 in [Reference Brundan and Stroppel8].
$-\nu - \tilde \rho$
) with respect to the dot action; see for instance Section 6.3 in [Reference Brundan and Stroppel8].
Now let us consider the category
![]() $\mathcal{\tilde O}$
of
$\mathcal{\tilde O}$
of
![]() $\mathfrak{\tilde g}$
-modules that admit a weight space decomposition with finite-dimensional weight spaces with respect to
$\mathfrak{\tilde g}$
-modules that admit a weight space decomposition with finite-dimensional weight spaces with respect to
![]() $\mathfrak{\tilde h}$
and whose set of weights is contained in the union of finitely many sets of the form
$\mathfrak{\tilde h}$
and whose set of weights is contained in the union of finitely many sets of the form
![]() $\{ \mu \in \mathfrak{\tilde h}^* \mid \mu \leq \lambda \}$
for
$\{ \mu \in \mathfrak{\tilde h}^* \mid \mu \leq \lambda \}$
for
![]() $\lambda \in \mathfrak{\tilde h}^*$
, where we write
$\lambda \in \mathfrak{\tilde h}^*$
, where we write
![]() $\leq$
for the partial order on
$\leq$
for the partial order on
![]() $\mathfrak{\tilde h}^*$
that is defined by
$\mathfrak{\tilde h}^*$
that is defined by
For all
![]() $\lambda \in \mathfrak{\tilde h}^*$
, the Verma module
$\lambda \in \mathfrak{\tilde h}^*$
, the Verma module
![]() $\Delta _\lambda$
of highest weight
$\Delta _\lambda$
of highest weight
![]() $\lambda$
, the dual Verma module
$\lambda$
, the dual Verma module
![]() $\nabla _\lambda$
, and the unique simple quotient
$\nabla _\lambda$
, and the unique simple quotient
![]() $L_\lambda$
of
$L_\lambda$
of
![]() $\Delta _\lambda$
(which is also the unique simple submodule of
$\Delta _\lambda$
(which is also the unique simple submodule of
![]() $\nabla _\lambda$
) are objects of
$\nabla _\lambda$
) are objects of
![]() $\mathcal{\tilde O}$
. Even though a
$\mathcal{\tilde O}$
. Even though a
![]() $\mathfrak{\tilde g}$
-module
$\mathfrak{\tilde g}$
-module
![]() $M$
in
$M$
in
![]() $\mathcal{\tilde O}$
does not need to admit a finite composition series, the composition multiplicities
$\mathcal{\tilde O}$
does not need to admit a finite composition series, the composition multiplicities
![]() $[ M\, :\, L_\mu ]$
are still (well-defined and) finite for
$[ M\, :\, L_\mu ]$
are still (well-defined and) finite for
![]() $\mu \in \mathfrak{\tilde h}^*$
(see Lemma 2.1.9 in [Reference Kumar17]). Now let us fix
$\mu \in \mathfrak{\tilde h}^*$
(see Lemma 2.1.9 in [Reference Kumar17]). Now let us fix
and write
![]() $\mathcal{\tilde O}_\lambda$
for the full subcategory of
$\mathcal{\tilde O}_\lambda$
for the full subcategory of
![]() $\mathcal{\tilde O}$
whose objects are the
$\mathcal{\tilde O}$
whose objects are the
![]() $\mathfrak{\tilde g}$
-modules
$\mathfrak{\tilde g}$
-modules
![]() $M$
in
$M$
in
![]() $\mathcal{\tilde O}$
such that
$\mathcal{\tilde O}$
such that
![]() $[ M\, :\, L_\mu ] = 0$
for all
$[ M\, :\, L_\mu ] = 0$
for all
![]() $\mu \in \mathfrak{\tilde h}^* \setminus \tilde W \boldsymbol{\cdot } \lambda$
. Furthermore, for
$\mu \in \mathfrak{\tilde h}^* \setminus \tilde W \boldsymbol{\cdot } \lambda$
. Furthermore, for
![]() $J \subseteq \tilde S$
, we write
$J \subseteq \tilde S$
, we write
![]() $\mathfrak{p}_J$
for the Levi subalgebra of
$\mathfrak{p}_J$
for the Levi subalgebra of
![]() $\mathfrak{\tilde g}$
corresponding to
$\mathfrak{\tilde g}$
corresponding to
![]() $J$
and we let
$J$
and we let
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}$
(or
$\mathcal{\tilde O}^{\mathfrak{p}_J}$
(or
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}_\lambda$
) be the full subcategory of
$\mathcal{\tilde O}^{\mathfrak{p}_J}_\lambda$
) be the full subcategory of
![]() $\mathcal{\tilde O}$
(or
$\mathcal{\tilde O}$
(or
![]() $\mathcal{\tilde O}_\lambda$
) whose objects are the locally
$\mathcal{\tilde O}_\lambda$
) whose objects are the locally
![]() $\mathfrak{p}_J$
-finite
$\mathfrak{p}_J$
-finite
![]() $\mathfrak{\tilde g}$
-modules in
$\mathfrak{\tilde g}$
-modules in
![]() $\mathcal{\tilde O}$
(or
$\mathcal{\tilde O}$
(or
![]() $\mathcal{\tilde O}_\lambda$
). As in the previous section, we write
$\mathcal{\tilde O}_\lambda$
). As in the previous section, we write
![]() $\Delta ^{\mathfrak{p}_J}_\mu$
for the largest locally
$\Delta ^{\mathfrak{p}_J}_\mu$
for the largest locally
![]() $\mathfrak{p}_J$
-finite quotient of the Verma module
$\mathfrak{p}_J$
-finite quotient of the Verma module
![]() $\Delta _\mu$
of highest weight
$\Delta _\mu$
of highest weight
![]() $\mu \in \mathfrak{\tilde h}^*$
and
$\mu \in \mathfrak{\tilde h}^*$
and
![]() $\nabla ^{\mathfrak{p}_J}_\mu$
for the largest locally
$\nabla ^{\mathfrak{p}_J}_\mu$
for the largest locally
![]() $\mathfrak{p}_J$
-finite submodule of
$\mathfrak{p}_J$
-finite submodule of
![]() $\nabla _\mu$
, and we call these
$\nabla _\mu$
, and we call these
![]() $\mathfrak{\tilde g}$
-modules the generalized Verma module and the dual generalized Verma module of highest weight
$\mathfrak{\tilde g}$
-modules the generalized Verma module and the dual generalized Verma module of highest weight
![]() $\mu$
with respect to
$\mu$
with respect to
![]() $\mathfrak{p}_J$
.
$\mathfrak{p}_J$
.
Now let
![]() $I \subseteq \tilde S$
such that
$I \subseteq \tilde S$
such that
![]() $\textrm{Stab}_{\tilde W}(\lambda ) = \tilde W_I$
. If
$\textrm{Stab}_{\tilde W}(\lambda ) = \tilde W_I$
. If
![]() $\lambda$
has positive (or negative) level then we parameterize the set of isomorphism classes of simple
$\lambda$
has positive (or negative) level then we parameterize the set of isomorphism classes of simple
![]() $\mathfrak{\tilde g}$
-modules in
$\mathfrak{\tilde g}$
-modules in
![]() $\mathcal{\tilde O}_\lambda$
by
$\mathcal{\tilde O}_\lambda$
by
![]() $X_\lambda\, :\!= \,\tilde W^I w_I$
(respectively
$X_\lambda\, :\!= \,\tilde W^I w_I$
(respectively
![]() $X_\lambda\, :\!= \,\tilde W^I$
) via the map
$X_\lambda\, :\!= \,\tilde W^I$
) via the map
![]() $w \mapsto L_{w\boldsymbol{\cdot }\lambda }$
, and this parametrization restricts to a bijection between the set of isomorphism classes of simple
$w \mapsto L_{w\boldsymbol{\cdot }\lambda }$
, and this parametrization restricts to a bijection between the set of isomorphism classes of simple
![]() $\mathfrak{\tilde g}$
-modules in
$\mathfrak{\tilde g}$
-modules in
![]() $\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
and the set
$\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
and the set
![]() $X_\lambda ^J \,:\!=\, {}^J \tilde W^I_{\textrm{reg}} w_I$
(respectively
$X_\lambda ^J \,:\!=\, {}^J \tilde W^I_{\textrm{reg}} w_I$
(respectively
![]() $X_\lambda ^J\, :\!= \,w_J{}^J \tilde W^I_{\textrm{reg}}$
) of representatives for the regular double cosets in
$X_\lambda ^J\, :\!= \,w_J{}^J \tilde W^I_{\textrm{reg}}$
) of representatives for the regular double cosets in
![]() $\tilde W_J \backslash \tilde W/ \tilde W_I$
(as defined in Appendix A). In order to apply the considerations from Section 1, we consider truncations of the category
$\tilde W_J \backslash \tilde W/ \tilde W_I$
(as defined in Appendix A). In order to apply the considerations from Section 1, we consider truncations of the category
![]() $\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
as follows: If
$\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
as follows: If
![]() $\lambda$
has negative level then for
$\lambda$
has negative level then for
![]() $w \in X_\lambda ^J$
, we write
$w \in X_\lambda ^J$
, we write
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
for the Serre subcategory of
$\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
for the Serre subcategory of
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda }$
generated by the simple
$\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda }$
generated by the simple
![]() $\mathfrak{\tilde g}$
-modules
$\mathfrak{\tilde g}$
-modules
![]() $L_{x\boldsymbol{\cdot }\lambda }$
with
$L_{x\boldsymbol{\cdot }\lambda }$
with
![]() $x \in X_\lambda ^{J, \leq w}$
, where we set
$x \in X_\lambda ^{J, \leq w}$
, where we set
Then,
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
is a highest weight category with weight poset
$\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
is a highest weight category with weight poset
![]() $( X_\lambda ^{J, \leq w}, \leq )$
by Lemma 3.7 in [Reference Shan, Varagnolo and Vasserot25], where
$( X_\lambda ^{J, \leq w}, \leq )$
by Lemma 3.7 in [Reference Shan, Varagnolo and Vasserot25], where
![]() $\leq$
denotes the Bruhat order and the standard objects and costandard objects are given by
$\leq$
denotes the Bruhat order and the standard objects and costandard objects are given by
![]() $\Delta ^{\mathfrak{p}_J}_{x\boldsymbol{\cdot }\lambda }$
and
$\Delta ^{\mathfrak{p}_J}_{x\boldsymbol{\cdot }\lambda }$
and
![]() $\nabla ^{\mathfrak{p}_J}_{x\boldsymbol{\cdot }\lambda }$
, respectively, for
$\nabla ^{\mathfrak{p}_J}_{x\boldsymbol{\cdot }\lambda }$
, respectively, for
![]() $x \in X_\lambda ^{J, \leq w}$
. If
$x \in X_\lambda ^{J, \leq w}$
. If
![]() $\lambda$
has positive level then for
$\lambda$
has positive level then for
![]() $w \in X_\lambda ^J$
, we write
$w \in X_\lambda ^J$
, we write
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
for the Serre quotient category of
$\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
for the Serre quotient category of
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda }$
by the Serre subcategory generated by the simple
$\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda }$
by the Serre subcategory generated by the simple
![]() $\mathfrak{\tilde g}$
-modules
$\mathfrak{\tilde g}$
-modules
![]() $L_{x\boldsymbol{\cdot }\lambda }$
for
$L_{x\boldsymbol{\cdot }\lambda }$
for
![]() $x \in X_\lambda ^J$
with
$x \in X_\lambda ^J$
with
![]() $x \nleq w$
, so that the simple objects of
$x \nleq w$
, so that the simple objects of
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
are naturally parameterized by the set
$\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
are naturally parameterized by the set
Then,
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
is a highest weight category with weight poset
$\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
is a highest weight category with weight poset
![]() $( X_\lambda ^{J, \leq w}, \geq\! )$
by Proposition 3.9 in [Reference Shan, Varagnolo and Vasserot25], where
$( X_\lambda ^{J, \leq w}, \geq\! )$
by Proposition 3.9 in [Reference Shan, Varagnolo and Vasserot25], where
![]() $\geq$
denotes the opposite Bruhat order and the standard objects and costandard objects are given by
$\geq$
denotes the opposite Bruhat order and the standard objects and costandard objects are given by
![]() $\Delta ^{\mathfrak{p}_J}_{x\boldsymbol{\cdot }\lambda }$
and
$\Delta ^{\mathfrak{p}_J}_{x\boldsymbol{\cdot }\lambda }$
and
![]() $\nabla ^{\mathfrak{p}_J}_{x\boldsymbol{\cdot }\lambda }$
, respectively, for
$\nabla ^{\mathfrak{p}_J}_{x\boldsymbol{\cdot }\lambda }$
, respectively, for
![]() $x \in X_\lambda ^{J, \leq w}$
. In either case (i.e. for
$x \in X_\lambda ^{J, \leq w}$
. In either case (i.e. for
![]() $\lambda$
of positive or negative level), we write
$\lambda$
of positive or negative level), we write
![]() $P^{\mathfrak{p}_J,\leq w}_{x\boldsymbol{\cdot }\lambda }$
for the projective cover of
$P^{\mathfrak{p}_J,\leq w}_{x\boldsymbol{\cdot }\lambda }$
for the projective cover of
![]() $L_{x\boldsymbol{\cdot }\lambda }$
in
$L_{x\boldsymbol{\cdot }\lambda }$
in
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
, for
$\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
, for
![]() $x \in X_\lambda ^{J, \leq w}$
, and we set
$x \in X_\lambda ^{J, \leq w}$
, and we set
so that
![]() $\mathcal{\tilde O}_{\lambda,\leq w}^{\mathfrak{p}_J}$
is equivalent to
$\mathcal{\tilde O}_{\lambda,\leq w}^{\mathfrak{p}_J}$
is equivalent to
![]() $A_{\lambda,\leq w}^{\mathfrak{p}_J}\text{-}\textrm{mod}$
.
$A_{\lambda,\leq w}^{\mathfrak{p}_J}\text{-}\textrm{mod}$
.
Remark 3.1.
For
![]() $\lambda$
of negative level, the fact that all of the truncated categories
$\lambda$
of negative level, the fact that all of the truncated categories
![]() $\mathcal{\tilde O}_{\lambda,\leq w}^{\mathfrak{p}_J}$
are highest weight categories implies that
$\mathcal{\tilde O}_{\lambda,\leq w}^{\mathfrak{p}_J}$
are highest weight categories implies that
![]() $\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
is a lower finite highest weight category with weight poset
$\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
is a lower finite highest weight category with weight poset
![]() $(X_\lambda ^J,\leq )$
, in the sense of Definition 3.50 in [Reference Brundan and Stroppel8], where as before, we write
$(X_\lambda ^J,\leq )$
, in the sense of Definition 3.50 in [Reference Brundan and Stroppel8], where as before, we write
![]() $\leq$
for the Bruhat order. For
$\leq$
for the Bruhat order. For
![]() $\lambda$
of positive level, the category
$\lambda$
of positive level, the category
![]() $\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
is an upper finite highest weight category with weight poset
$\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
is an upper finite highest weight category with weight poset
![]() $(X_\lambda ^J,\geq )$
in the sense of [Reference Brundan and Stroppel8, Definition 3.34] because every simple
$(X_\lambda ^J,\geq )$
in the sense of [Reference Brundan and Stroppel8, Definition 3.34] because every simple
![]() $\mathfrak{\tilde g}$
-module in
$\mathfrak{\tilde g}$
-module in
![]() $\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
has a projective cover in
$\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
has a projective cover in
![]() $\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
which admits a filtration by generalized Verma modules; see [Reference Rocha-Caridi and Wallach22, Section 4].
$\mathcal{\tilde O}_\lambda ^{\mathfrak{p}_J}$
which admits a filtration by generalized Verma modules; see [Reference Rocha-Caridi and Wallach22, Section 4].
As in the preceding section, we want to use Koszul duality as a tool to compute the dimensions of
![]() $\textrm{Ext}$
-groups in
$\textrm{Ext}$
-groups in
![]() $\mathcal{\tilde O}_{\lambda,\leq w}^{\mathfrak{p}_J}$
. This is possible by the following result; see Theorem 3.12 in [Reference Shan, Varagnolo and Vasserot25].
$\mathcal{\tilde O}_{\lambda,\leq w}^{\mathfrak{p}_J}$
. This is possible by the following result; see Theorem 3.12 in [Reference Shan, Varagnolo and Vasserot25].
Theorem 3.2.
Let
![]() $I,J \subsetneq \tilde S$
and let
$I,J \subsetneq \tilde S$
and let
![]() $\lambda \in - \tilde \rho - \tilde X^+$
and
$\lambda \in - \tilde \rho - \tilde X^+$
and
![]() $\mu \in - \tilde \rho + \tilde X^+$
such that
$\mu \in - \tilde \rho + \tilde X^+$
such that
![]() $\textrm{Stab}_{\tilde W}(\lambda ) = \tilde W_I$
and
$\textrm{Stab}_{\tilde W}(\lambda ) = \tilde W_I$
and
![]() $\textrm{Stab}_{\tilde W}(\mu ) = \tilde W_J$
. Then, for
$\textrm{Stab}_{\tilde W}(\mu ) = \tilde W_J$
. Then, for
![]() $w \in X_\lambda ^J$
and
$w \in X_\lambda ^J$
and
![]() $u \in X_\mu ^I$
, the algebras
$u \in X_\mu ^I$
, the algebras
![]() $A_{\lambda,\leq w}^{\mathfrak{p}_J}$
and
$A_{\lambda,\leq w}^{\mathfrak{p}_J}$
and
![]() $A_{\mu,\leq u}^{\mathfrak{p}_I}$
are standard Koszul, and their Koszul duals are given by
$A_{\mu,\leq u}^{\mathfrak{p}_I}$
are standard Koszul, and their Koszul duals are given by
Now let us return to a weight
![]() $\lambda \in ( {-} \tilde \rho + \tilde X^+ ) \cup ( {-} \tilde \rho - \tilde X^+ )$
with
$\lambda \in ( {-} \tilde \rho + \tilde X^+ ) \cup ( {-} \tilde \rho - \tilde X^+ )$
with
![]() $\lambda \neq - \rho$
and subsets
$\lambda \neq - \rho$
and subsets
![]() $I,J \subsetneq \tilde S$
such that
$I,J \subsetneq \tilde S$
such that
![]() $\textrm{Stab}_{\tilde W}(\lambda ) = \tilde W_I$
. Let us further fix a weight
$\textrm{Stab}_{\tilde W}(\lambda ) = \tilde W_I$
. Let us further fix a weight
![]() $\mu \in ( {-} \tilde \rho + \tilde X^+ ) \cup ( {-} \tilde \rho - \tilde X^+ )$
with
$\mu \in ( {-} \tilde \rho + \tilde X^+ ) \cup ( {-} \tilde \rho - \tilde X^+ )$
with
![]() $\textrm{Stab}_{\tilde W}(\mu ) = \tilde W_J$
such that
$\textrm{Stab}_{\tilde W}(\mu ) = \tilde W_J$
such that
![]() $\mu$
has negative (or positive) level if
$\mu$
has negative (or positive) level if
![]() $\lambda$
has positive (or negative) level. For
$\lambda$
has positive (or negative) level. For
![]() $w \in X_\lambda ^J$
, we set
$w \in X_\lambda ^J$
, we set
For
![]() $x \in X_\lambda ^{J,\leq w}$
, we further write
$x \in X_\lambda ^{J,\leq w}$
, we further write
![]() $e^{\mathfrak{p}_J,\leq w}_{\lambda,x}$
for the idempotent in
$e^{\mathfrak{p}_J,\leq w}_{\lambda,x}$
for the idempotent in
![]() $A^{\mathfrak{p}_J}_{\lambda,\leq w}$
corresponding to the canonical projection
$A^{\mathfrak{p}_J}_{\lambda,\leq w}$
corresponding to the canonical projection
![]() $\textrm{P}^{\mathfrak{p}_J}_{\lambda,\leq w} \to P^{\mathfrak{p}_J,\leq w}_{x\boldsymbol{\cdot }\lambda }$
and
$\textrm{P}^{\mathfrak{p}_J}_{\lambda,\leq w} \to P^{\mathfrak{p}_J,\leq w}_{x\boldsymbol{\cdot }\lambda }$
and
![]() $f^{\mathfrak{p}_J,\leq w}_{\lambda,x}$
for the idempotent in the Koszul dual
$f^{\mathfrak{p}_J,\leq w}_{\lambda,x}$
for the idempotent in the Koszul dual
![]() $( A^{\mathfrak{p}_J}_{\lambda,\leq w} )^!$
corresponding to the canonical projection
$( A^{\mathfrak{p}_J}_{\lambda,\leq w} )^!$
corresponding to the canonical projection
![]() $\textrm{L}^{\mathfrak{p}_J}_{\lambda,\leq w} \to L_{x\boldsymbol{\cdot }\lambda }$
. Then, again by Theorem 3.12 in [Reference Shan, Varagnolo and Vasserot25], the isomorphism
$\textrm{L}^{\mathfrak{p}_J}_{\lambda,\leq w} \to L_{x\boldsymbol{\cdot }\lambda }$
. Then, again by Theorem 3.12 in [Reference Shan, Varagnolo and Vasserot25], the isomorphism
from Theorem 3.2 can be chosen in such a way that it maps
![]() $e^{\mathfrak{p}_I,\leq w^{-1}}_{\mu,x^{-1}}$
to
$e^{\mathfrak{p}_I,\leq w^{-1}}_{\mu,x^{-1}}$
to
![]() $f^{\mathfrak{p}_J,\leq w}_{\lambda,x}$
for all
$f^{\mathfrak{p}_J,\leq w}_{\lambda,x}$
for all
![]() $x \in X_\lambda ^J$
. In particular, if we write
$x \in X_\lambda ^J$
. In particular, if we write
![]() $L^{\mathfrak{p}_J,\leq w,!}_{\lambda,x}$
for the simple
$L^{\mathfrak{p}_J,\leq w,!}_{\lambda,x}$
for the simple
![]() $( A^{\mathfrak{p}_J}_{\lambda,\leq w} )^!$
-module corresponding to
$( A^{\mathfrak{p}_J}_{\lambda,\leq w} )^!$
-module corresponding to
![]() $x \in X_\lambda ^{J,\leq w}$
(as described in Section 1) then the functor
$x \in X_\lambda ^{J,\leq w}$
(as described in Section 1) then the functor
induced by the aforementioned isomorphism sends the simple
![]() $( A^{\mathfrak{p}_J}_{\lambda,\leq w} )^!$
-module
$( A^{\mathfrak{p}_J}_{\lambda,\leq w} )^!$
-module
![]() $L^{\mathfrak{p}_J,\leq w,!}_{\lambda,x}$
to the simple
$L^{\mathfrak{p}_J,\leq w,!}_{\lambda,x}$
to the simple
![]() $\mathfrak{\tilde g}$
-module
$\mathfrak{\tilde g}$
-module
![]() $L_{x^{-1} \boldsymbol{\cdot } \mu }$
. We can now prove the main result of this section; it is an analogue of Theorem 2.2 in the setting of affine Kac-Moody algebras.
$L_{x^{-1} \boldsymbol{\cdot } \mu }$
. We can now prove the main result of this section; it is an analogue of Theorem 2.2 in the setting of affine Kac-Moody algebras.
Theorem 3.3.
Let
![]() $\lambda \in ( {-} \tilde \rho + \tilde X^+ ) \cup ( {-} \tilde \rho - \tilde X^+ )$
and
$\lambda \in ( {-} \tilde \rho + \tilde X^+ ) \cup ( {-} \tilde \rho - \tilde X^+ )$
and
![]() $I,J \subsetneq \tilde S$
such that
$I,J \subsetneq \tilde S$
such that
![]() $\textrm{Stab}_{\tilde W}(\lambda ) = \tilde W_I$
. If
$\textrm{Stab}_{\tilde W}(\lambda ) = \tilde W_I$
. If
![]() $\lambda$
has negative level then we have
$\lambda$
has negative level then we have
for all
![]() $x,y \in X_\lambda ^J$
, and if
$x,y \in X_\lambda ^J$
, and if
![]() $\lambda$
has positive level then we have
$\lambda$
has positive level then we have
for all
![]() $x,y \in X_\lambda ^J$
.
$x,y \in X_\lambda ^J$
.
Proof. Let us start by observing that by Theorems 3.42 and 3.59 in [Reference Brundan and Stroppel8], we have
for all
![]() $i \geq 0$
and
$i \geq 0$
and
![]() $w \in X_\lambda ^J$
such that
$w \in X_\lambda ^J$
such that
![]() $x,y \leq w$
; hence, it suffices to prove the formulas in the theorem for the highest weight category
$x,y \leq w$
; hence, it suffices to prove the formulas in the theorem for the highest weight category
![]() $\mathcal{\tilde O}_{\lambda,\leq w}^{\mathfrak{p}_J}$
.
$\mathcal{\tilde O}_{\lambda,\leq w}^{\mathfrak{p}_J}$
.
Next, for
![]() $x \in X_\lambda ^{J,\leq w}$
, let us write
$x \in X_\lambda ^{J,\leq w}$
, let us write
![]() $\hat L^{\mathfrak{p}_J,\leq w}_{x\boldsymbol{\cdot }\lambda }$
and
$\hat L^{\mathfrak{p}_J,\leq w}_{x\boldsymbol{\cdot }\lambda }$
and
![]() $\hat \Delta ^{\mathfrak{p}_J,\leq w}_{x\boldsymbol{\cdot }\lambda }$
for the canonical graded lifts of
$\hat \Delta ^{\mathfrak{p}_J,\leq w}_{x\boldsymbol{\cdot }\lambda }$
for the canonical graded lifts of
![]() $L_{x\boldsymbol{\cdot }\lambda }$
and
$L_{x\boldsymbol{\cdot }\lambda }$
and
![]() $\Delta ^{\mathfrak{p}_J}_{x\boldsymbol{\cdot }\lambda }$
, respectively, in the category
$\Delta ^{\mathfrak{p}_J}_{x\boldsymbol{\cdot }\lambda }$
, respectively, in the category
![]() $\mathcal{\tilde O}_{\lambda,\leq w,\textrm{gr}}^{\mathfrak{p}_J}$
of graded modules over a Koszul graded version
$\mathcal{\tilde O}_{\lambda,\leq w,\textrm{gr}}^{\mathfrak{p}_J}$
of graded modules over a Koszul graded version
![]() $\hat A^{\mathfrak{p}_J}_{\lambda,\leq w}$
of
$\hat A^{\mathfrak{p}_J}_{\lambda,\leq w}$
of
![]() $A^{\mathfrak{p}_J}_{\lambda,\leq w}$
. Then, according to Lemma 1.3, the polynomials
$A^{\mathfrak{p}_J}_{\lambda,\leq w}$
. Then, according to Lemma 1.3, the polynomials
with
![]() $x,y,z \in X_\lambda ^{J,\leq w}$
satisfy the inversion formula
$x,y,z \in X_\lambda ^{J,\leq w}$
satisfy the inversion formula
and for
![]() $\mu \in ( {-} \tilde \rho + \tilde X^+ ) \cup ( {-} \tilde \rho - \tilde X^+ )$
with
$\mu \in ( {-} \tilde \rho + \tilde X^+ ) \cup ( {-} \tilde \rho - \tilde X^+ )$
with
![]() $\textrm{Stab}_{\tilde W}(\mu ) = \tilde W_J$
and such that
$\textrm{Stab}_{\tilde W}(\mu ) = \tilde W_J$
and such that
![]() $\mu$
has negative (or positive) level if
$\mu$
has negative (or positive) level if
![]() $\lambda$
has positive (or negative) level, we have
$\lambda$
has positive (or negative) level, we have
by Lemma 1.4 and the above discussion of Koszul duality for
![]() $\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
.
$\mathcal{\tilde O}^{\mathfrak{p}_J}_{\lambda,\leq w}$
.
As in the proof of Theorem 2.2, we first consider a special case of the formulas in the theorem, which we will then use to prove the general statement: Let
![]() $\nu \in - \tilde \rho - \tilde X^+$
with
$\nu \in - \tilde \rho - \tilde X^+$
with
![]() $\nu \neq - \tilde \rho$
and
$\nu \neq - \tilde \rho$
and
![]() $\textrm{Stab}_{\tilde W}(\nu ) = \{ e \}$
, so that
$\textrm{Stab}_{\tilde W}(\nu ) = \{ e \}$
, so that
![]() $L_{w_J\boldsymbol{\cdot }\nu } = \Delta ^{\mathfrak{p}_J}_{w_J\boldsymbol{\cdot }\nu }$
and
$L_{w_J\boldsymbol{\cdot }\nu } = \Delta ^{\mathfrak{p}_J}_{w_J\boldsymbol{\cdot }\nu }$
and
for all
![]() $x \in X_\nu ^J$
by Theorem 3.56 in [Reference Brundan and Stroppel8].
$x \in X_\nu ^J$
by Theorem 3.56 in [Reference Brundan and Stroppel8].
Now one can show by induction on the length of
![]() $y \in X_\nu ^J$
that the validity of the Kazhdan-Lusztig character formula in
$y \in X_\nu ^J$
that the validity of the Kazhdan-Lusztig character formula in
![]() $\mathcal{\tilde O}_\nu$
(as conjectured in this case by G. Lusztig [Reference Lusztig19] and proven by M. Kashiwara and T. Tanisaki [Reference Kashiwara and Tanisaki15]) and of its parabolic analogue in
$\mathcal{\tilde O}_\nu$
(as conjectured in this case by G. Lusztig [Reference Lusztig19] and proven by M. Kashiwara and T. Tanisaki [Reference Kashiwara and Tanisaki15]) and of its parabolic analogue in
![]() $\mathcal{\tilde O}_\nu ^{\mathfrak{p}_J}$
(see Section 3.3 in [Reference Lanini, Ram and Sobaje18]) implies that
$\mathcal{\tilde O}_\nu ^{\mathfrak{p}_J}$
(see Section 3.3 in [Reference Lanini, Ram and Sobaje18]) implies that
for all
![]() $x,y \in X_\nu ^J$
, exactly as in the proof of Proposition C.2 in [Reference Jantzen12].Footnote
4
This implies that
$x,y \in X_\nu ^J$
, exactly as in the proof of Proposition C.2 in [Reference Jantzen12].Footnote
4
This implies that
for all
![]() $w \in X_\nu ^J$
and
$w \in X_\nu ^J$
and
![]() $x,y \in X_\nu ^{J,\leq w}$
, and by equations (3.1) and (A1), we further have
$x,y \in X_\nu ^{J,\leq w}$
, and by equations (3.1) and (A1), we further have
Now suppose that
![]() $\lambda$
has negative level. By Lemma 5.10 in [Reference Shan, Varagnolo and Vasserot25] (see also Remark 4.2 in [Reference Ko14]), the ordinary translation functor
$\lambda$
has negative level. By Lemma 5.10 in [Reference Shan, Varagnolo and Vasserot25] (see also Remark 4.2 in [Reference Ko14]), the ordinary translation functor
admits a graded lift
for all
![]() $w \in X_\lambda$
, and the latter restricts to a functor from
$w \in X_\lambda$
, and the latter restricts to a functor from
![]() $\mathcal{\tilde O}_{\nu,\leq w,\textrm{gr}}^{\mathfrak{p}_J}$
to
$\mathcal{\tilde O}_{\nu,\leq w,\textrm{gr}}^{\mathfrak{p}_J}$
to
![]() $\mathcal{\tilde O}_{\lambda,\leq w,\textrm{gr}}^{\mathfrak{p}_J}$
for
$\mathcal{\tilde O}_{\lambda,\leq w,\textrm{gr}}^{\mathfrak{p}_J}$
for
![]() $w \in X_\lambda ^J$
, as in the proof of Theorem 2.2. Still as in the proof of Theorem 2.2, we conclude that
$w \in X_\lambda ^J$
, as in the proof of Theorem 2.2. Still as in the proof of Theorem 2.2, we conclude that
for all
![]() $w \in X_\lambda ^J$
and
$w \in X_\lambda ^J$
and
![]() $y,z \in X_\lambda ^{J,\leq w}$
, and using the inversion formulas from equation (3.1) and Theorem A.1, it follows that
$y,z \in X_\lambda ^{J,\leq w}$
, and using the inversion formulas from equation (3.1) and Theorem A.1, it follows that
for all
![]() $w \in X_\lambda ^J$
and
$w \in X_\lambda ^J$
and
![]() $x,z \in X_\lambda ^{J,\leq w}$
, matching the first formula in the theorem. Furthermore, for a weight
$x,z \in X_\lambda ^{J,\leq w}$
, matching the first formula in the theorem. Furthermore, for a weight
![]() $\mu \in - \tilde \rho + \tilde X^+$
with
$\mu \in - \tilde \rho + \tilde X^+$
with
![]() $\mu \neq - \tilde \rho$
and
$\mu \neq - \tilde \rho$
and
![]() $\textrm{Stab}_{\tilde W}(\mu ) = \tilde W_J$
, equation (3.2) yields
$\textrm{Stab}_{\tilde W}(\mu ) = \tilde W_J$
, equation (3.2) yields
for all
![]() $w \in X_\mu ^I$
and
$w \in X_\mu ^I$
and
![]() $x,y,z \leq X_\mu ^{I,\leq w}$
, and by relabeling, we obtain the second equation in the theorem.
$x,y,z \leq X_\mu ^{I,\leq w}$
, and by relabeling, we obtain the second equation in the theorem.
Remark 3.4. The first formula in Theorem 3.3 is also obtained (using different methods) in the proof of Theorem 4.10 in [Reference Ko14].
Acknowledgments
The author would like to thank Donna Testerman and Wolfgang Soergel for their helpful discussions and comments. This work was funded by the Swiss National Science Foundation under the grant FNS 200020_207730 and by the Singapore MOE grant R-146-000-294-133.
Competing interests
The author declares none.
Appendix A: Coxeter groups and Kazhdan-Lusztig polynomials
In this appendix, we summarize some important results about Kazhdan-Lusztig type combinatorics, and we prove the “double parabolic inversion formula” which was used in the proof of Theorem 3.3. We follow the conventions of [Reference Soergel24] and refer the reader to that article for more details and further references. Let
![]() $W$
be a Coxeter group with a finite set of simple reflections
$W$
be a Coxeter group with a finite set of simple reflections
![]() $S \subseteq W$
, so
$S \subseteq W$
, so
![]() $W$
has a presentation of the form
$W$
has a presentation of the form
for certain
![]() $m_{st} \in \{ 2,3,4,\ldots \} \cup \{ \infty \}$
, where by convention, the relation
$m_{st} \in \{ 2,3,4,\ldots \} \cup \{ \infty \}$
, where by convention, the relation
![]() $(st)^{m_{st}} = e$
is void if
$(st)^{m_{st}} = e$
is void if
![]() $m_{st} = \infty$
. We write
$m_{st} = \infty$
. We write
![]() $\ell \colon W \to \mathbb{Z}_{\geq 0}$
for the length function and
$\ell \colon W \to \mathbb{Z}_{\geq 0}$
for the length function and
![]() $\leq$
for the Bruhat order on
$\leq$
for the Bruhat order on
![]() $W$
. For a subset
$W$
. For a subset
![]() $I \subseteq S$
, we call
$I \subseteq S$
, we call
![]() $W_I\, :\!= \,\langle I \rangle$
the parabolic subgroup of
$W_I\, :\!= \,\langle I \rangle$
the parabolic subgroup of
![]() $W$
corresponding to
$W$
corresponding to
![]() $I$
. For any
$I$
. For any
![]() $x \in W$
, the coset
$x \in W$
, the coset
![]() $x W_I$
contains a unique element of minimal length, and the latter is also minimal in
$x W_I$
contains a unique element of minimal length, and the latter is also minimal in
![]() $x W_I$
with respect to the Bruhat order. We write
$x W_I$
with respect to the Bruhat order. We write
![]() $W^I$
for the set of elements
$W^I$
for the set of elements
![]() $x \in W$
that have minimal length in the coset
$x \in W$
that have minimal length in the coset
![]() $W^I$
and remark that for
$W^I$
and remark that for
![]() $x \in W^I$
and
$x \in W^I$
and
![]() $w \in W_I$
, we have
$w \in W_I$
, we have
![]() $\ell (xw) = \ell (x) + \ell (w)$
. Analogously, we write
$\ell (xw) = \ell (x) + \ell (w)$
. Analogously, we write
![]() ${}^{I}{W}$
for the set of elements
${}^{I}{W}$
for the set of elements
![]() $y \in W$
that have minimal length in the coset
$y \in W$
that have minimal length in the coset
![]() $W_I y$
and remark that for
$W_I y$
and remark that for
![]() $y \in{}^{I}{W}$
and
$y \in{}^{I}{W}$
and
![]() $w \in W_I$
, we have
$w \in W_I$
, we have
![]() $\ell (wy) = \ell (w) + \ell (y)$
. If
$\ell (wy) = \ell (w) + \ell (y)$
. If
![]() $W_I$
is finite, then we write
$W_I$
is finite, then we write
![]() $w_I$
for the longest element of
$w_I$
for the longest element of
![]() $W_I$
. Then,
$W_I$
. Then,
![]() $W^I w_I$
is precisely the set of elements
$W^I w_I$
is precisely the set of elements
![]() $x \in W$
that have maximal length in the coset
$x \in W$
that have maximal length in the coset
![]() $x W_I$
and
$x W_I$
and
![]() $w_I{}^{I}{W}$
is the set of elements
$w_I{}^{I}{W}$
is the set of elements
![]() $y \in W$
that have maximal length in the coset
$y \in W$
that have maximal length in the coset
![]() $W_I y$
.
$W_I y$
.
The Hecke algebra of
![]() $W$
is the associative
$W$
is the associative
![]() $\mathbb{Z}[v^{\pm 1}]$
-algebra
$\mathbb{Z}[v^{\pm 1}]$
-algebra
![]() $\mathcal{H} = \mathcal{H}_W$
with generators
$\mathcal{H} = \mathcal{H}_W$
with generators
![]() $H_s$
for
$H_s$
for
![]() $s \in S$
, subject to the quadratic relations
$s \in S$
, subject to the quadratic relations
and the braid relations
for
![]() $s,t \in S$
. Using the quadratic relations, it is straightforward to see that there are two
$s,t \in S$
. Using the quadratic relations, it is straightforward to see that there are two
![]() $\mathcal{H}$
-modules
$\mathcal{H}$
-modules
of rank one such that
![]() $H_s$
acts on
$H_s$
acts on
![]() $\textrm{triv}_W$
by multiplication with
$\textrm{triv}_W$
by multiplication with
![]() $v^{-1}$
and on
$v^{-1}$
and on
![]() $\textrm{sign}_W$
by multiplication with
$\textrm{sign}_W$
by multiplication with
![]() $-v$
for all
$-v$
for all
![]() $s \in S$
, and using the braid relations, one can show that for
$s \in S$
, and using the braid relations, one can show that for
![]() $w \in W$
with a reduced expression
$w \in W$
with a reduced expression
![]() $w = s_1 \cdots s_m$
, the element
$w = s_1 \cdots s_m$
, the element
![]() $H_w\, :\!= \,H_{s_1} \cdots H_{s_m} \in \mathcal{H}$
is independent of the choice of reduced expression for
$H_w\, :\!= \,H_{s_1} \cdots H_{s_m} \in \mathcal{H}$
is independent of the choice of reduced expression for
![]() $w$
. The elements
$w$
. The elements
![]() $H_w$
with
$H_w$
with
![]() $w \in W$
are invertible and form a
$w \in W$
are invertible and form a
![]() $\mathbb{Z}[v^{\pm 1}]$
-basis of
$\mathbb{Z}[v^{\pm 1}]$
-basis of
![]() $\mathcal{H}$
. We define the bar involution of
$\mathcal{H}$
. We define the bar involution of
![]() $\mathcal{H}$
to be the unique ring homomorphism
$\mathcal{H}$
to be the unique ring homomorphism
![]() $\overline{\phantom{A}} \colon \mathcal{H} \to \mathcal{H}$
with
$\overline{\phantom{A}} \colon \mathcal{H} \to \mathcal{H}$
with
![]() $\overline{v} = v^{-1}$
and
$\overline{v} = v^{-1}$
and
![]() $\overline{H_x} = H_{x^{-1}}^{-1}$
, and we call an element
$\overline{H_x} = H_{x^{-1}}^{-1}$
, and we call an element
![]() $H \in \mathcal{H}$
self-dual if
$H \in \mathcal{H}$
self-dual if
![]() $\overline{H} = H$
. For any
$\overline{H} = H$
. For any
![]() $x \in W$
, there exists a unique self-dual element
$x \in W$
, there exists a unique self-dual element
![]() $\underline{H}_x \in \mathcal{H}$
such that
$\underline{H}_x \in \mathcal{H}$
such that
![]() $\underline{H}_x \in H_x + \sum _{y\lt x} v \mathbb{Z}[v] \cdot H_y$
, and the elements
$\underline{H}_x \in H_x + \sum _{y\lt x} v \mathbb{Z}[v] \cdot H_y$
, and the elements
![]() $\underline{H}_x$
with
$\underline{H}_x$
with
![]() $x \in W$
form the Kazhdan-Lusztig basis of
$x \in W$
form the Kazhdan-Lusztig basis of
![]() $\mathcal{H}$
. The Kazhdan-Lusztig polynomial
$\mathcal{H}$
. The Kazhdan-Lusztig polynomial
![]() $h_{y,x}$
corresponding to two elements
$h_{y,x}$
corresponding to two elements
![]() $x,y \in W$
is defined by the equality
$x,y \in W$
is defined by the equality
and the inverse Kazhdan-Lusztig polynomial
![]() $h^{y,x}$
is defined by
$h^{y,x}$
is defined by
Now let us fix a subset
![]() $I \subseteq S$
and consider the spherical
$I \subseteq S$
and consider the spherical
![]() $\mathcal{H}$
-module
$\mathcal{H}$
-module
and the anti-spherical
![]() $\mathcal{H}$
-module
$\mathcal{H}$
-module
The elements
![]() $M_x = 1 \otimes H_x \in \mathcal{M}$
and
$M_x = 1 \otimes H_x \in \mathcal{M}$
and
![]() $N_x = 1 \otimes H_x \in \mathcal{N}$
for
$N_x = 1 \otimes H_x \in \mathcal{N}$
for
![]() $x \in{}^{I}{W}$
form bases of
$x \in{}^{I}{W}$
form bases of
![]() $\mathcal{M}$
and
$\mathcal{M}$
and
![]() $\mathcal{N}$
, respectively, and the bar involution on
$\mathcal{N}$
, respectively, and the bar involution on
![]() $\mathcal{H}$
induces involutions
$\mathcal{H}$
induces involutions
![]() $\overline{\phantom{A}} \colon \mathcal{M} \to \mathcal{M}$
and
$\overline{\phantom{A}} \colon \mathcal{M} \to \mathcal{M}$
and
![]() $\overline{\phantom{A}} \colon \mathcal{N} \to \mathcal{N}$
. For any
$\overline{\phantom{A}} \colon \mathcal{N} \to \mathcal{N}$
. For any
![]() $x \in{}^{I}{W}$
, there is a unique self-dual element
$x \in{}^{I}{W}$
, there is a unique self-dual element
![]() $\underline{M}_x \in \mathcal{M}$
and a unique self-dual element
$\underline{M}_x \in \mathcal{M}$
and a unique self-dual element
![]() $\underline{N}_x \in \mathcal{N}$
with
$\underline{N}_x \in \mathcal{N}$
with
and the elements
![]() $\underline{M}_x$
and
$\underline{M}_x$
and
![]() $\underline{N}_x$
with
$\underline{N}_x$
with
![]() $x \in{}^{I}{W}$
form the Kazhdan-Lusztig bases of
$x \in{}^{I}{W}$
form the Kazhdan-Lusztig bases of
![]() $\mathcal{M}$
and
$\mathcal{M}$
and
![]() $\mathcal{N}$
, respectively. For later use, we note that the right
$\mathcal{N}$
, respectively. For later use, we note that the right
![]() $\mathcal{H}$
-module homomorphism
$\mathcal{H}$
-module homomorphism
satisfies
![]() $\psi (\underline{H}_x) = \underline{N}_x$
for all
$\psi (\underline{H}_x) = \underline{N}_x$
for all
![]() $x \in{}^{I}{W}$
and
$x \in{}^{I}{W}$
and
![]() $\psi ( \underline{H}_x ) = 0$
for
$\psi ( \underline{H}_x ) = 0$
for
![]() $x \in W \setminus{}^{I}{W}$
; see the proof of Proposition 3.4 in [Reference Soergel24]. The spherical Kazhdan-Lusztig polynomial
$x \in W \setminus{}^{I}{W}$
; see the proof of Proposition 3.4 in [Reference Soergel24]. The spherical Kazhdan-Lusztig polynomial
![]() $m_{y,x}$
and the anti-spherical Kazhdan-Lusztig polynomial
$m_{y,x}$
and the anti-spherical Kazhdan-Lusztig polynomial
![]() $n_{y,x}$
corresponding to
$n_{y,x}$
corresponding to
![]() $x,y \in{}^{I}{W}$
are defined by the equalities
$x,y \in{}^{I}{W}$
are defined by the equalities
and as before, we define the inverse spherical Kazhdan-Lusztig polynomial
![]() $m^{y,x}$
and the inverse anti-spherical Kazhdan-Lusztig polynomial
$m^{y,x}$
and the inverse anti-spherical Kazhdan-Lusztig polynomial
![]() $n^{y,x}$
by
$n^{y,x}$
by
As a consequence, we have the inversion formulas
for all
![]() $x,y \in{}^{I}{W}$
. When the choice of
$x,y \in{}^{I}{W}$
. When the choice of
![]() $I \subseteq S$
is not clear from the context, we occasionally write
$I \subseteq S$
is not clear from the context, we occasionally write
Now for
![]() $I \subseteq S$
such that
$I \subseteq S$
such that
![]() $W_I$
is finite, consider the element
$W_I$
is finite, consider the element
and observe that we have
![]() $H_s \cdot 1_I = 1_I \cdot H_s = v^{-1} \cdot 1_I$
for all
$H_s \cdot 1_I = 1_I \cdot H_s = v^{-1} \cdot 1_I$
for all
![]() $s \in I$
; see Proposition 2.9 in [Reference Soergel24]. By the proof of Proposition 3.4 in [Reference Soergel24], the
$s \in I$
; see Proposition 2.9 in [Reference Soergel24]. By the proof of Proposition 3.4 in [Reference Soergel24], the
![]() $\mathbb{Z}[v^{\pm 1}]$
-linear map
$\mathbb{Z}[v^{\pm 1}]$
-linear map
![]() $\varphi \colon \mathcal{M} \to \mathcal{H}$
with
$\varphi \colon \mathcal{M} \to \mathcal{H}$
with
![]() $M_x \mapsto 1_I \cdot H_x$
for all
$M_x \mapsto 1_I \cdot H_x$
for all
![]() $x \in{}^{I}{W}$
is a homomorphism of right
$x \in{}^{I}{W}$
is a homomorphism of right
![]() $\mathcal{H}$
-modules with
$\mathcal{H}$
-modules with
![]() $\varphi (\underline{M}_x) = \underline{H}_{w_I x}$
for all
$\varphi (\underline{M}_x) = \underline{H}_{w_I x}$
for all
![]() $x \in{}^{I}{W}$
, and it induces an isomorphism between the right
$x \in{}^{I}{W}$
, and it induces an isomorphism between the right
![]() $\mathcal{H}$
-modules
$\mathcal{H}$
-modules
![]() $\mathcal{M}$
and
$\mathcal{M}$
and
![]() $1_I \cdot \mathcal{H}$
. In particular, we have
$1_I \cdot \mathcal{H}$
. In particular, we have
for all
![]() $y \in{}^{I}{W}$
. Using the anti-involution
$y \in{}^{I}{W}$
. Using the anti-involution
![]() $i$
from the proof of [Reference Soergel24, Theorem 2.7], we further obtain
$i$
from the proof of [Reference Soergel24, Theorem 2.7], we further obtain
and
![]() $\underline{H}_{xw_I} \in \mathcal{H} \cdot 1_I$
for all
$\underline{H}_{xw_I} \in \mathcal{H} \cdot 1_I$
for all
![]() $x,y \in W^I$
. These observations will be useful later on.
$x,y \in W^I$
. These observations will be useful later on.
In the following, we want to combine the “spherical” and the “anti-spherical” type Kazhdan-Lusztig combinatorics for two different parabolic subgroups of
![]() $W$
corresponding to subsets
$W$
corresponding to subsets
![]() $I, J \subseteq S$
such that
$I, J \subseteq S$
such that
![]() $W_I$
is finite. To that end, we consider the
$W_I$
is finite. To that end, we consider the
![]() $\mathbb{Z}[v^{\pm 1}]$
-submodule
$\mathbb{Z}[v^{\pm 1}]$
-submodule
![]() $\mathcal{N}_J \cdot 1_I$
of
$\mathcal{N}_J \cdot 1_I$
of
![]() $\mathcal{N}_J$
, which by the above discussion can be considered as a generalization of both the anti-spherical
$\mathcal{N}_J$
, which by the above discussion can be considered as a generalization of both the anti-spherical
![]() $\mathcal{H}$
-module
$\mathcal{H}$
-module
![]() $\mathcal{N}_J$
and the spherical
$\mathcal{N}_J$
and the spherical
![]() $\mathcal{H}$
-module
$\mathcal{H}$
-module
![]() $\mathcal{M}_I \cong 1_I \cdot \mathcal{H}$
(or strictly speaking, the analogous left
$\mathcal{M}_I \cong 1_I \cdot \mathcal{H}$
(or strictly speaking, the analogous left
![]() $\mathcal{H}$
-module
$\mathcal{H}$
-module
![]() $\mathcal{H} \cdot 1_I$
). This approach draws some inspiration from Subsection 2.2 in [Reference Lanini, Ram and Sobaje18]. We first need to discuss some properties of parabolic double cosets.
$\mathcal{H} \cdot 1_I$
). This approach draws some inspiration from Subsection 2.2 in [Reference Lanini, Ram and Sobaje18]. We first need to discuss some properties of parabolic double cosets.
Let us fix two subsets
![]() $I, J \subseteq S$
. The properties of the double cosets in
$I, J \subseteq S$
. The properties of the double cosets in
![]() $W_J \backslash W/ W_I$
that we list in this paragraph follow from Exercise §1.3 in [Reference Bourbaki7, Chapter IV]; see also [Reference Billey, Konvalinka, Petersen, Slofstra and Tenner6, Subsection 2.2]. For every element
$W_J \backslash W/ W_I$
that we list in this paragraph follow from Exercise §1.3 in [Reference Bourbaki7, Chapter IV]; see also [Reference Billey, Konvalinka, Petersen, Slofstra and Tenner6, Subsection 2.2]. For every element
![]() $x \in W$
, the double coset
$x \in W$
, the double coset
![]() $W_J x W_I$
has a unique element of minimal length, and the latter is also minimal in
$W_J x W_I$
has a unique element of minimal length, and the latter is also minimal in
![]() $W_J x W_I$
with respect to the Bruhat order. The set of elements of
$W_J x W_I$
with respect to the Bruhat order. The set of elements of
![]() $W$
that have minimal length in their
$W$
that have minimal length in their
![]() $(W_J,W_I)$
double coset is precisely
$(W_J,W_I)$
double coset is precisely
hence,
![]() ${}^{J}{W}^I$
is a set of
${}^{J}{W}^I$
is a set of
![]() $(W_J,W_I)$
double coset representatives. For
$(W_J,W_I)$
double coset representatives. For
![]() $z \in{}^{J}{W}^I$
and
$z \in{}^{J}{W}^I$
and
![]() $H\, :\!= \,J \cap z I z^{-1}$
, an element
$H\, :\!= \,J \cap z I z^{-1}$
, an element
![]() $x \in W_J$
satisfies
$x \in W_J$
satisfies
![]() $xz \in W^I$
if and only if
$xz \in W^I$
if and only if
![]() $x \in W_J^H$
, and the map
$x \in W_J^H$
, and the map
![]() $W_J^H \times W_I \to W_J z W_I$
with
$W_J^H \times W_I \to W_J z W_I$
with
![]() $(x,y) \mapsto xzy$
is a bijection with
$(x,y) \mapsto xzy$
is a bijection with
![]() $\ell (xzy) = \ell (x) + \ell (z) + \ell (y)$
. Analogously, for
$\ell (xzy) = \ell (x) + \ell (z) + \ell (y)$
. Analogously, for
![]() $H^\prime\, :\!= \,z^{-1} J z \cap I$
, an element
$H^\prime\, :\!= \,z^{-1} J z \cap I$
, an element
![]() $y \in W_I$
satisfies
$y \in W_I$
satisfies
![]() $zy \in{}^{J}{W}$
if and only if
$zy \in{}^{J}{W}$
if and only if
![]() $y \in{}^{H^\prime }{W}_I$
, and the map
$y \in{}^{H^\prime }{W}_I$
, and the map
![]() $W_J \times{}^{H^\prime }{W}_I$
with
$W_J \times{}^{H^\prime }{W}_I$
with
![]() $(x,y) \mapsto xzy$
is a bijection with
$(x,y) \mapsto xzy$
is a bijection with
![]() $\ell (xzy) = \ell (x) + \ell (z) + \ell (y)$
. We say that the double coset
$\ell (xzy) = \ell (x) + \ell (z) + \ell (y)$
. We say that the double coset
![]() $W_J z W_I$
(with
$W_J z W_I$
(with
![]() $z \in{}^{J}{W}^I$
) is regular if
$z \in{}^{J}{W}^I$
) is regular if
![]() $J \cap z I z^{-1} = \varnothing$
, and we write
$J \cap z I z^{-1} = \varnothing$
, and we write
for the set of minimal length representatives of the regular
![]() $(W_J,W_I)$
-double cosets.
$(W_J,W_I)$
-double cosets.
Now let
![]() $I,J \subseteq S$
such that
$I,J \subseteq S$
such that
![]() $W_I$
is finite and consider the
$W_I$
is finite and consider the
![]() $\mathbb{Z}[v^{\pm 1}]$
-submodule
$\mathbb{Z}[v^{\pm 1}]$
-submodule
![]() $\mathcal{N}_J \cdot 1_I$
of
$\mathcal{N}_J \cdot 1_I$
of
![]() $\mathcal{N}_J$
. Observe that for
$\mathcal{N}_J$
. Observe that for
![]() $x \in{}^{J}{W}^I$
,
$x \in{}^{J}{W}^I$
,
![]() $y \in W_J$
, and
$y \in W_J$
, and
![]() $z \in W_I$
such that
$z \in W_I$
such that
![]() $\ell (yxz) = \ell (y) + \ell (x) + \ell (z)$
, we have
$\ell (yxz) = \ell (y) + \ell (x) + \ell (z)$
, we have
whence
![]() $\mathcal{N}_J \cdot 1_I$
is spanned over
$\mathcal{N}_J \cdot 1_I$
is spanned over
![]() $\mathbb{Z}[v^{\pm 1}]$
by the elements
$\mathbb{Z}[v^{\pm 1}]$
by the elements
![]() $N_x \cdot 1_I$
with
$N_x \cdot 1_I$
with
![]() $x \in{}^{J}{W}^I$
. If the double coset
$x \in{}^{J}{W}^I$
. If the double coset
![]() $W_J x W_I$
is non-regular, then we can choose
$W_J x W_I$
is non-regular, then we can choose
![]() $s \in J \cap x I x^{-1}$
and
$s \in J \cap x I x^{-1}$
and
![]() $t = x^{-1} s x \in I$
, and we compute
$t = x^{-1} s x \in I$
, and we compute
Since
![]() $\mathcal{N}_J$
is free over
$\mathcal{N}_J$
is free over
![]() $\mathbb{Z}[v^{\pm 1}]$
, this implies that
$\mathbb{Z}[v^{\pm 1}]$
, this implies that
![]() $N_x \cdot 1_I = 0$
and that
$N_x \cdot 1_I = 0$
and that
![]() $\mathcal{N}_J \cdot 1_I$
is spanned over
$\mathcal{N}_J \cdot 1_I$
is spanned over
![]() $\mathbb{Z}[v^{\pm 1}]$
by the elements
$\mathbb{Z}[v^{\pm 1}]$
by the elements
![]() $N_x \cdot 1_I$
with
$N_x \cdot 1_I$
with
![]() $x \in{}^{J}{W}^I_{\textrm{reg}}$
. For
$x \in{}^{J}{W}^I_{\textrm{reg}}$
. For
![]() $x \in{}^{J}{W}^I_{\textrm{reg}}$
, we have
$x \in{}^{J}{W}^I_{\textrm{reg}}$
, we have
because
![]() $xw \in{}^{J}{W}$
for all
$xw \in{}^{J}{W}$
for all
![]() $x \in W_I$
. Since the elements
$x \in W_I$
. Since the elements
![]() $N_x$
with
$N_x$
with
![]() $x \in{}^{J}{W}$
form a
$x \in{}^{J}{W}$
form a
![]() $\mathbb{Z}[v^{\pm 1}]$
-basis of
$\mathbb{Z}[v^{\pm 1}]$
-basis of
![]() $\mathcal{N}_J$
, we conclude that the elements
$\mathcal{N}_J$
, we conclude that the elements
![]() $N_x \cdot 1_I$
with
$N_x \cdot 1_I$
with
![]() $x \in{}^{J}{W}^I_{\textrm{reg}}$
form a
$x \in{}^{J}{W}^I_{\textrm{reg}}$
form a
![]() $\mathbb{Z}[v^{\pm 1}]$
-basis of
$\mathbb{Z}[v^{\pm 1}]$
-basis of
![]() $\mathcal{N}_J \cdot 1_I$
. Furthermore, still for
$\mathcal{N}_J \cdot 1_I$
. Furthermore, still for
![]() $x \in{}^{J}{W}^I_{\textrm{reg}}$
, we have
$x \in{}^{J}{W}^I_{\textrm{reg}}$
, we have
![]() $\underline{H}_{x w_I} \in \mathcal{H} \cdot 1_I$
(as observed above) and
$\underline{H}_{x w_I} \in \mathcal{H} \cdot 1_I$
(as observed above) and
![]() $\underline{N}_{xw_I} = \psi ( \underline{H}_{xw_I} ) \in \mathcal{N}_J \cdot 1_I$
. Thus, the elements
$\underline{N}_{xw_I} = \psi ( \underline{H}_{xw_I} ) \in \mathcal{N}_J \cdot 1_I$
. Thus, the elements
![]() $\underline{N}_{x w_I}$
with
$\underline{N}_{x w_I}$
with
![]() $x \in{}^{J}{W}^I_{\textrm{reg}}$
form another basis of
$x \in{}^{J}{W}^I_{\textrm{reg}}$
form another basis of
![]() $\mathcal{N}_J \cdot 1_I$
, which we call the Kazhdan-Lusztig basis. Now we can define polynomials
$\mathcal{N}_J \cdot 1_I$
, which we call the Kazhdan-Lusztig basis. Now we can define polynomials
![]() $p_{y,x}$
and
$p_{y,x}$
and
![]() $p^{y,x}$
for
$p^{y,x}$
for
![]() $x,y \in{}^{J}{W}^I_{\textrm{reg}}$
by the equalities
$x,y \in{}^{J}{W}^I_{\textrm{reg}}$
by the equalities
We could call these polynomials double parabolic Kazhdan-Lusztig polynomials, although as we will presently observe, they match the usual (anti-spherical or inverse spherical) parabolic Kazhdan-Lusztig polynomials for a suitable choice of parameters. Indeed, we have
and therefore
![]() $p_{y,x} = n^J_{yw_I,xw_I}$
, and by applying the homomorphism
$p_{y,x} = n^J_{yw_I,xw_I}$
, and by applying the homomorphism
![]() $\psi \colon \mathcal{H} \to \mathcal{N}_J$
to the equality
$\psi \colon \mathcal{H} \to \mathcal{N}_J$
to the equality
we obtain
 \begin{equation*} \sum _{ \substack { z \in W^I, \\ zw_I \in {}^{J}{W} } } ({-}1)^{\ell (y)+\ell (z)} \cdot m_I^{y^{-1},z^{-1}} \cdot \underline {N}_{z w_I} = N_y \cdot 1_I = \sum _{ x \in {}^{J}{W}^I_{\textrm {reg}} } ({-}1)^{\ell (y)+\ell (x)} \cdot p^{y,x} \cdot \underline {N}_{xw_I} \end{equation*}
\begin{equation*} \sum _{ \substack { z \in W^I, \\ zw_I \in {}^{J}{W} } } ({-}1)^{\ell (y)+\ell (z)} \cdot m_I^{y^{-1},z^{-1}} \cdot \underline {N}_{z w_I} = N_y \cdot 1_I = \sum _{ x \in {}^{J}{W}^I_{\textrm {reg}} } ({-}1)^{\ell (y)+\ell (x)} \cdot p^{y,x} \cdot \underline {N}_{xw_I} \end{equation*}
and therefore
![]() $p^{y,x} = m_I^{y^{-1},x^{-1}}$
. As an immediate consequence of these observations, we get the following double parabolic inversion formula:
$p^{y,x} = m_I^{y^{-1},x^{-1}}$
. As an immediate consequence of these observations, we get the following double parabolic inversion formula:
Theorem A.1.
Let
![]() $I,J \subseteq S$
such that
$I,J \subseteq S$
such that
![]() $W_I$
is finite. For
$W_I$
is finite. For
![]() $x,y \in{}^{J}{W}^I_{\textrm{reg}}$
, we have
$x,y \in{}^{J}{W}^I_{\textrm{reg}}$
, we have
Proof. This follows from the definition of the polynomials
![]() $p_{z,x}$
and
$p_{z,x}$
and
![]() $p^{z,y}$
and the fact that
$p^{z,y}$
and the fact that
as observed above.