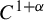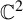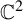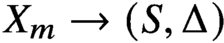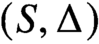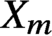17 results
Shadowing and hyperbolicity for linear delay difference equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
Some asymptotic formulae for torsion in homotopy groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1339-1357
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic Lyapunov–Perron regular points and smooth invariant measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 17 June 2022, pp. 2177-2200
- Print publication:
- July 2023
-
- Article
- Export citation
Topological and geometric hyperbolicity criteria for polynomial automorphisms of
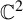 ${\mathbb {C}^2}$
${\mathbb {C}^2}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2151-2171
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Ahlfors regularity and fractal dimension of Smale spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 29 April 2021, pp. 2281-2332
- Print publication:
- July 2022
-
- Article
- Export citation
Nonspecial varieties and generalised Lang–Vojta conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 10 February 2021, e11
-
- Article
-
- You have access
- Open access
- Export citation
Shadowing and structural stability for operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 961-980
- Print publication:
- April 2021
-
- Article
- Export citation
Rigidity Properties for Hyperbolic Generalizations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 November 2019, pp. 66-76
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Numerical Study of Partially Conservative Moment Equations in Kinetic Theory
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 981-1011
- Print publication:
- April 2017
-
- Article
- Export citation
A Well-Posed and Discretely Stable Perfectly Matched Layer for Elastic Wave Equations in Second Order Formulation
-
- Journal:
- Communications in Computational Physics / Volume 11 / Issue 5 / May 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1643-1672
- Print publication:
- May 2012
-
- Article
- Export citation
Modified Baer-Nunziato Model for the Simulation of Interfaces Between Compressible Fluids
-
- Journal:
- Communications in Computational Physics / Volume 9 / Issue 4 / April 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1040-1055
- Print publication:
- April 2011
-
- Article
- Export citation
Hyperbolic relaxation models for granular flows
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 44 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 27 January 2010, pp. 371-400
- Print publication:
- March 2010
-
- Article
- Export citation
LIMITS OF HYPERCYCLIC AND SUPERCYCLIC OPERATOR MATRICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 367-376
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
ROBUST HETERODIMENSIONAL CYCLES AND $C^1$-GENERIC DYNAMICS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 3 / July 2008
- Published online by Cambridge University Press:
- 10 December 2007, pp. 469-525
- Print publication:
- July 2008
-
- Article
- Export citation
THE ROLE OF FUNNELS AND PUNCTURES IN THE GROMOV HYPERBOLICITY OF RIEMANN SURFACES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 49 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 30 May 2006, pp. 399-425
-
- Article
-
- You have access
- Export citation
Some Convergence Results for p-Harmonic Functions on Metric Measure Spaces
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 1 / July 2003
- Published online by Cambridge University Press:
- 25 June 2003, pp. 226-246
- Print publication:
- July 2003
-
- Article
- Export citation
Averaging method for differential equations perturbed by dynamical systems
-
- Journal:
- ESAIM: Probability and Statistics / Volume 6 / 2002
- Published online by Cambridge University Press:
- 15 November 2002, pp. 33-88
- Print publication:
- 2002
-
- Article
- Export citation