Some asymptotic formulae for torsion in homotopy groups

Abstract

Inspired by a remarkable work of Félix, Halperin, and Thomas on the asymptotic estimation of the ranks of rational homotopy groups, and more recent works of Wu and the authors on local hyperbolicity, we prove two asymptotic formulae for torsion rank of homotopy groups, one using ordinary homology and one using K-theory. We use these to obtain explicit quantitative asymptotic lower bounds on the torsion rank of the homotopy groups for many interesting spaces after suspension, including Moore spaces, Eilenberg–MacLane spaces, complex projective spaces, complex Grassmannians, Milnor hypersurfaces, and unitary groups.

1 Introduction

The homotopy groups of a simply connected $CW$ -complex Y of finite type have the form

$$\begin{align*}\pi_i(Y)\cong \left(\mathop{\oplus}_{d_i}\mathbb{Z}\right)\oplus \mathop{\oplus}\limits_{\substack{\mathrm{prime}~p\\t \in \mathbb{Z}^+}}\left(\mathop{\oplus}\limits_{k_{p,t}} \mathbb{Z}/p^t\right), \end{align*}$$

where $d_i$ and $k_{p,t}$ are the rank of the free summands and the $\mathbb {Z}/p^t$ -summands of $\pi _i(Y),$ respectively. Denote $\mathrm{rank}_{0}(\pi _i(Y)):=d_i$ and $\mathrm{rank}_{\mathbb {Z}/p^t}(\pi _i(Y)):=k_{p,t}$ .

In the remarkable work [FHT], Félix, Halperin, and Thomas proved an asymptotic formula for the ranks $\mathrm{rank}_{0}(\pi _i(Y))$ of the free part of the homotopy groups. In particular, they showed that if Y is finite and $\mathrm{rank}_{0}(\pi _i(Y))\neq 0$ for infinitely many $i\in \mathbb {Z}^{+}$ , then there is a constant $\delta>1$ such that for N large enough

$$\begin{align*}\sum_{i=N+2}^{N+\mathrm{dim}(Y)} \mathrm{rank}_{0}(\pi_i(Y))\geq \delta^{N}, \end{align*}$$

which they interpret as a strong “regularity” property for the ranks $\mathrm{rank}_{0}(\pi _i(Y))$ of the free part of the homotopy groups. Concerning the ranks $\mathrm{rank}_{\mathbb {Z}/p^t}(\pi _i(Y))$ of the torsion part of the homotopy groups, they further raised the following natural question, which was rephrased in an explicit form by Wu and the second author in [HW, Question 1.8].

Question 1.1 Are there “regularity” properties of the torsion subgroups of the homotopy groups $\pi _i(Y)$ as $i\rightarrow \infty $ ?

In this paper, we study the above question by providing estimates for the ranks $\mathrm{rank}_{\mathbb {Z}/p^t}(\pi _i(Y))$ in certain cases. In particular, we give quantitative refinements of results of the authors and Wu, from the papers [Boy1, Boy2, HW]. The methods of these papers implied more than were stated in the theorems: the statements were always that the volume of p-torsion in the homotopy groups of various spaces grows exponentially, but actually the methods were completely constructive, and with more work one can extract concrete exponential lower bounds. The extraction of these lower bounds is the business of this paper.

The proof of each of our main theorems (1.2 and 1.7) begins with the combinatorics of free Lie algebras, which have been well understood since long before Félix, Halperin, and Thomas’s celebrated theorem. We use in particular some results of Babenko [Bab] and Lambrechts [Lam], both of which are more general. From this common beginning, the proof of each theorem is then complicated in a different way; we elaborate briefly after each theorem statement.

Recent work of Burklund and Senger [BS] has greatly advanced our understanding of these phenomena: they finish a story begun by Henn [Hen] and Iriye [Iri] and show that the radii of convergence of the p-local “homotopy” and “loop-homology” power series are equal. Again, we discuss each of our theorems in light of this.

1.1 Results via homology

We first give our quantitative refinement of the main result of [Boy2]. To state the results, for any integer $q\geq 2$ , define a function

$$\begin{align*}f_q(x)= \bigg(1 - \frac{x}{x-1} \frac{1}{\varphi}\bigg) \cdot \frac{1}{x} \varphi^{x} - c x \varphi^{\frac{x}{2}} - \kappa \lvert \psi \rvert^x \end{align*}$$

for $x\geq 2$ , where:

• • $\varphi $ is the unique positive real root of the degree $q+1$ polynomial $P(z)=z^{q+1} - z - 1$ ,

• • $\psi $ is the root of $\frac {P(z)}{(z - \varphi )}$ for which the absolute value $\lvert \varphi \rvert $ is maximized (i.e., the “second largest root of $P(z)$ after $\varphi $ in absolute value”),

• • $c= 2(q+2)(1+ \varphi )$ , and

• • $\kappa = (q+1)\left(1+ \frac {1}{\lvert \psi \rvert }\right)$ .

We have the properties:

• • $2^{\frac {1}{q+1}}< \varphi < 1 + \frac {1}{q}$ , and

• • for any $\varepsilon>0$ , once x is large enough we have

  $$\begin{align*}f_q(x) \geq (1- \varepsilon) \bigg(1 - \frac{1}{\varphi}\bigg) \cdot \frac{1}{x} \varphi^{x}> (1- \varepsilon) \bigg(1 - 2^{-\frac{1}{q+1}}\bigg) \cdot \frac{1}{x} 2^{\frac{x}{q+1}}. \end{align*}$$

We will use the function $f_q(x)$ with its properties freely in this subsection.

Let $P^{q+1}(p^r)$ be the Moore space defined as the mapping cone of the degree $p^r$ map $S^{q}\rightarrow S^q$ . The following theorem provides an asymptotic formula for the p-local homotopy groups under a homological condition.

Theorem 1.2 Let Y be a simply connected $CW$ -complex, let $p \neq 2$ be prime, and let $s \leq r \in \mathbb {Z}^+$ . If there exists a map

$$ \begin{align*} \mu: P^{q+1}(p^r) \longrightarrow Y \end{align*} $$

for some $q\geq 2$ , such that the induced map

$$ \begin{align*}(\Omega \mu)_* : H_*(\Omega P^{q+1}(p^r);{\mathbb{Z}/p^s}) \longrightarrow H_*(\Omega Y;{\mathbb{Z}/p^s}) \end{align*} $$

is an injection, then we have the bound

$$ \begin{align*} \sum_{t=s}^r \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{N+1}(Y)) \geq f_q(N). \end{align*} $$

In particular, for any $\varepsilon>0$ , once N is large enough we have

$$\begin{align*}\sum_{t=s}^r \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{N+1}(Y))>(1- \varepsilon) \bigg(1 - 2^{-\frac{1}{q+1}}\bigg) \cdot \frac{1}{N} 2^{\frac{N}{q+1}}. \end{align*}$$

Algebraically, Theorem 1.2 depends on the structure of the module of boundaries in a free Lie algebra over a finite field. It is the need to take boundaries which complicates the story relative to Babenko and Lambrechts’s work. This is dealt with in Section 2.3, using a result of Cohen, Moore, and Neisendorfer [CMN].

Using [Boy2, Proposition 10.12], the hypotheses of Theorem 1.2 simplify in the case that $Y=\Sigma X$ is a suspension, as follows:

Theorem 1.3 Let X be a connected $CW$ -complex, let $p \neq 2$ be prime, and let $s \leq r \in \mathbb {Z}^+$ . Suppose that $H_*(X; {\mathbb {Z}/p^s})$ has finite type. If there exists a map

$$ \begin{align*}\mu: P^{q+1}(p^r) \longrightarrow \Sigma X\end{align*} $$

for some $q\geq 2$ , such that

$$ \begin{align*}\mu_* : \widetilde{H}_*(P^{q+1}(p^r);{\mathbb{Z}/p^s}) \longrightarrow \widetilde{H}_*(\Sigma X;{\mathbb{Z}/p^s})\end{align*} $$

is an injection, then we have the bound

$$ \begin{align*}\sum_{t=s}^r \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{N+1}(\Sigma X)) \geq f_q(N).\end{align*} $$

In particular, for any $\varepsilon>0$ , once N is large enough we have

$$\begin{align*}\sum_{t=s}^r \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{N+1}(\Sigma X))> (1- \varepsilon) \left(1 - 2^{-\frac{1}{q+1}}\right) \cdot \frac{1}{N} 2^{\frac{N}{q+1}}. \end{align*}$$

The spaces X and Y in Theorems 1.2 and 1.3 can be infinite. The asymptotic formulae in both theorems bound the ranks of the p-local homotopy groups from below by an exponential function. In particular, they strengthen a recent result of the first author on local hyperbolicity [Boy2, Theorems 1.5 and 1.6].

Note also that if $s=r$ , then the sum appearing on the left-hand side in the conclusions of Theorems 1.2 and 1.3 simplifies to $\mathrm{rank}_{{\mathbb {Z}/p^r}}(\pi _{N+1}(\Sigma X)),$ and this simplification will apply in all the examples.

Theorem 1.3 has interesting applications. For instance, the Hurewicz theorem immediately gives the following example, which refines [Boy2, Corollary 2.4]. We caution the reader to bear in mind that when a space X satisfies the hypotheses of Theorem 1.3, the conclusions of that theorem refer to the suspension $\Sigma X$ , rather than to X itself.

Example 1.4 Let X be a connected $CW$ -complex, and let $p \neq 2$ be prime. Suppose that $H_*(X; {\mathbb {Z}/p^r})$ has finite type and that the lowest-dimensional nontrivial reduced integral homology group contains a $\mathbb {Z}/p^r$ -summand. Then X satisfies the hypotheses of Theorem 1.3 with $s=r$ and $q=\mathrm {conn}(X)+2$ .

The identity map on a Moore space automatically satisfies the hypotheses of Theorem 1.2 (alternatively, apply Example 1.4), so we obtain the following.

Example 1.5 Let p be an odd prime and $q \geq 2$ . Then $P^{q}(p^r)$ satisfies the hypotheses of Theorem 1.2 with $s=r$ and $\mu $ equal to the identity map on $\Sigma P^{q}(p^r) = P^{q+1}(p^r)$ . It follows that

$$ \begin{align*}\mathrm{rank}_{\mathbb{Z}/p^r}(\pi_{N+1}(P^{q+1}(p^r)) \geq f_q(N).\end{align*} $$

This strengthens a result of Wu and the second author on the $\mathbb {Z}/p^r$ -hyperbolicity of $P^{q+1}(p^r)$ [HW, Theorem 1.6].

It is enlightening to compare this result from what could be deduced already from Burklund and Senger’s work [BS]. It follows from their Corollary A.5 that the radius of convergence of the series $\sum _{N=1}^\infty \dim _{{\mathbb {Z}/p}}(\pi _N(P^{q+1}(p^r)) \otimes {\mathbb {Z}/p}) \cdot t^N$ is precisely $\frac {1}{\varphi }$ . Since $P^{q+1}(p^r)$ is rationally elliptic (being rationally contractible), this power series really is describing the torsion. Example 1.5 adds information in two ways: first, by giving a concrete function as a lower bound for all N, and second, by saying something about summands isomorphic to ${\mathbb {Z}/p^r}$ in particular, rather than p-torsion in general.

Another interesting consequence of Example 1.4 is a torsion bound for an Eilenberg–MacLane space after suspension. In particular, the following immediate consequence gives a quantitative refinement of [Boy2, Example 2.5].

Example 1.6 Let p be an odd prime and $q \geq 2$ . Then $K(\mathbb {Z}/p^r, q-1)$ is $(q-2)$ -connected, and the least-dimensional nontrivial homology group is $H_{q-1}(K(\mathbb {Z}/p^r, q-1)) \cong \mathbb {Z}/p^r$ . By Example 1.4, $K(\mathbb {Z}/p^r, q-1)$ satisfies the hypotheses of Theorem 1.3 with $s=r$ .

1.2 Results via K-theory

Denote by

$$\begin{align*}\mathrm{rank}_{p}(\pi_{i}(\Sigma X))=\sum_{t=1}^\infty \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{i}(\Sigma X)) \end{align*}$$

the rank of the p-torsion summands of $\pi _{i}(\Sigma X)$ . Our other main result refines the main theorem of [Boy1] to a quantitative statement under a K-theoretical condition is the following.

Theorem 1.7 (Weak version of Theorem 3.3)

Let p be an odd prime, and let X be a path connected space having the p-local homotopy type of a finite $CW$ -complex. Suppose that there exists a map

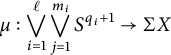$$ \begin{align*} \mu : \bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1} \to \Sigma X \end{align*} $$

with $1 \leq q_1 < q_2 < \dots < q_\ell $ , such that the map

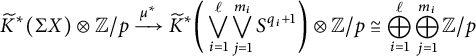$$ \begin{align*} \widetilde{K}^*(\Sigma X) \otimes {\mathbb{Z}/p} \xrightarrow{\mu^*} \widetilde{K}^*\bigg(\bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1}\bigg) \otimes {\mathbb{Z}/p} \cong \bigoplus_{i=1}^\ell \bigoplus_{j=1}^{m_i} {\mathbb{Z}/p} \end{align*} $$

is a surjection.

Then, for any $\varepsilon>0$ , once the multiple $M=mg'$ of

$$ \begin{align*} g'=\gcd(q_1, \dots, q_\ell,2(p-1)) \end{align*} $$

is large enough we have

$$ \begin{align*}\mathrm{rank}_{p}(\pi_{M}(\Sigma X))\geq \frac{1}{M^{1+\varepsilon}}\varphi^{\left(\frac{\mathrm{conn}(X)+1}{\dim(X)+1}\right)M},\end{align*} $$

where $\varphi $ is the unique positive real root of the degree $q_\ell $ polynomial

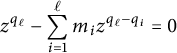$$ \begin{align*}z^{q_\ell} - \sum_{i=1}^\ell m_i z^{q_\ell - q_i} = 0\end{align*} $$

(in particular, $\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }} = (\sum _{i=1}^\ell m_i)^{\frac {1}{\max (q_1, \dots , q_\ell )}}$ ), $\mathrm {conn}(X)$ is the p-local connectivity of X, and $\dim (X)$ is the rational cohomological dimension of X.

A stronger estimate is provided by Theorem 3.3 with Remark 3.4 at the end of the paper. In particular, the asymptotic formulae in both theorems bound the ranks of the p-local homotopy groups from below by an exponential function. Unlike with Theorem 1.2, it is not necessary to take boundaries to prove Theorem 1.7, but the topological picture is difficult. The difficulty arises ultimately from an interaction between the James construction and the Adams operations, which as far as the authors know originates in the paper [Sel] of Selick on which [Boy1] is modeled, and manifests combinatorially as Condition (*) in the last section. This condition means that the “Lie algebra” one is ultimately able to find a copy of in homotopy groups “lags”—appearing in higher dimensions than one might expect. In the end, this shows up as, for example, the factor of $\left(\frac {\mathrm{{conn}(X)+1}}{\dim (X)+1}\right)$ in the exponent in Theorem 1.7.

Theorem 1.7 has interesting applications. For instance, let $\mathrm{Gr}_k(\mathbb {C}^n)$ be the Grassmannian of k-dimensional complex linear subspaces of $\mathbb {C}^n$ , which is simply connected and of complex dimension $k(n-k)$ . Recall $\mathrm{Gr}_1(\mathbb {C}^n)\cong \mathbb {C}P^{n-1}$ . In [Boy1, Example 2.6], it is shown that when $n\geq 3$ and $0<k<n$ there is a map

$$\begin{align*}S^3\vee S^5 \stackrel{}{\longrightarrow}\Sigma \mathrm{Gr}_k(\mathbb{C}^n), \end{align*}$$

which induces a surjection on $\widetilde {K}^\ast (~)\otimes \mathbb {Z}/p$ for all odd primes p. Applying Theorem 1.7, we must find the positive root of $z^4-z^2-1$ , which is $\sqrt {\frac {1+ \sqrt {5}}{2}}$ . Tidying the resulting formula a little, we obtain the following corollary, which strengthens [Boy1, Examples 2.5 and 2.6].

Corollary 1.8 Let p be an odd prime, $n\geq 3$ and $0<k<n$ . Then, for any $\varepsilon>0$ , once m is large enough we have

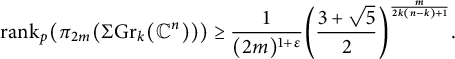$$\begin{align*} \mathrm{rank}_{p}(\pi_{2m}(\Sigma \mathrm{Gr}_k(\mathbb{C}^n)))\geq \frac{1}{(2m)^{1+\varepsilon}}\bigg(\frac{3+\sqrt{5}}{2}\bigg)^{\frac{m}{2k(n-k)+1}}. \end{align*}$$

Similarly, let $H_{n, \ell }$ be the Milnor hypersurface defined by

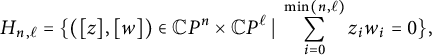$$\begin{align*}H_{n, \ell}=\{([z], [w])\in \mathbb{C}P^n\times \mathbb{C}P^\ell~|~ \sum\limits_{i=0}^{\mathrm{min}(n, \ell)} z_iw_i=0\}, \end{align*}$$

which is simply connected and of complex dimension $n+\ell -1$ . In [Boy1, Example 2.7], it is showed that when $n\geq 2$ and $\ell \geq 3$ there is a map

$$\begin{align*}S^3\vee S^5 \stackrel{}{\longrightarrow}\Sigma H_{n, \ell,} \end{align*}$$

which induces a surjection on $\widetilde {K}^\ast (~)\otimes \mathbb {Z}/p$ for all odd primes p. Therefore, the following corollary follows immediately from Theorem 1.7, which strengthens [Boy1, Example 2.7].

Corollary 1.9 Let p be an odd prime, $n\geq 2$ and $\ell \geq 3$ . Then, for any $\varepsilon>0$ , once m is large enough we have

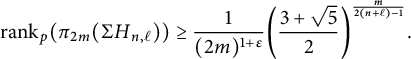$$\begin{align*} \mathrm{rank}_{p}(\pi_{2m}(\Sigma H_{n, \ell}))\geq \frac{1}{(2m)^{1+\varepsilon}}\bigg(\frac{3+\sqrt{5}}{2}\bigg)^{\frac{m}{2(n+\ell)-1}}. \end{align*}$$

Consider the nth unitary group $U(n)$ which is connected and of real dimension $n^2$ . In [Boy1, Example 2.8], it is showed that when $n\geq 3$ there is a map

$$\begin{align*}S^3\vee S^5 \stackrel{}{\longrightarrow}U(n), \end{align*}$$

which induces a surjection on $\widetilde {K}^\ast (~)\otimes \mathbb {Z}/p$ for all odd primes p. It is clear that this map can be lifted to the special unitary group $SU(n)$ , which is $2$ -connected and of real dimension $n^2-1$ . Therefore, the following corollary follows immediately from Theorem 1.7, which strengthens [Boy1, Example 2.8].

Corollary 1.10 Let p be an odd prime and $n\geq 3$ . Then, for any $\varepsilon>0$ , once m is large enough we have

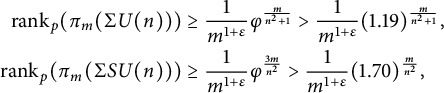$$\begin{align*}\begin{aligned} \mathrm{rank}_{p}(\pi_{m}(\Sigma U(n)))&\geq \frac{1}{m^{1+\varepsilon}}\varphi^{\frac{m}{n^2+1}}>\frac{1}{m^{1+\varepsilon}} (1.19)^{\frac{m}{n^2+1}}, \\ \mathrm{rank}_{p}(\pi_{m}(\Sigma SU(n)))&\geq \frac{1}{m^{1+\varepsilon}}\varphi^{\frac{3m}{n^2}}>\frac{1}{m^{1+\varepsilon}} (1.70)^{\frac{m}{n^2}}, \end{aligned} \end{align*}$$

where $\varphi $ is the unique positive real root of $z^5-z^2-1=0$ .

The structure of this paper is as follows: Section 2 treats the algebra and combinatorics. Section 2.2 treats free Lie algebras without a differential, and Section 2.3 studies the module of boundaries in the differential case. These results are then used to prove the main theorems in Section 3.

2 Algebra

2.1 Complex arithmetic

Lemma 2.1 Let S be a finite set of positive integers, let $g = \gcd (S)$ , and let $\eta \in \mathbb {C}$ be nonzero. Then $\eta ^g$ is a positive real if and only if $\eta ^i$ is a positive real for all $i \in S$ .

Proof The “only if” direction follows from the fact that g divides each member of S. For the “if” direction, Bezout’s Lemma gives $\alpha _i \in \mathbb {Z}$ for each $i \in S$ such that ${\sum _i \alpha _i \cdot i = g}$ . Thus, if each $\eta ^i$ is a positive real, we get

$$ \begin{align*}\eta^g = \eta^{\sum_i \alpha_i \cdot i} = \prod_i (\eta^i)^{\alpha_i},\end{align*} $$

which is a product of powers of positive reals, hence also a positive real.

Lemma 2.2 Let $c_0, \dots , c_{k-1} \in \mathbb {Z}_{\geq 0}$ , with $c_0 \geq 1$ . The polynomial

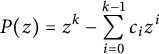$$ \begin{align*}P(z) = z^{k} - \sum_{i=0}^{k-1} c_i z^i\end{align*} $$

has precisely one positive real root, $\varphi $ , which occurs with multiplicity one, and satisfies $\varphi \geq 1$ . The other roots $\eta $ satisfy $|\eta | \leq \varphi $ , with equality holding if and only if $\eta $ is the product of $\varphi $ with a gth root of unity, where $g=\gcd (\{i \mid c_i \neq 0\}\cup \{k\})$ .

Proof The number of sign changes between consecutive coefficients in P is 1, so P has precisely one positive real root by Descartes’ rule of signs. Call this root $\varphi $ . Rearranging, we have $\varphi ^k = \sum _{i=0}^{k-1} c_i \varphi ^i$ . Since $c_0 \geq 1$ , we must have $\varphi ^k \geq 1$ , so $\varphi \geq 1$ .

Suppose that $\eta \in \mathbb {C}$ is a root of P. Taking modulus and applying the triangle inequality, we obtain

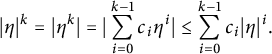$$ \begin{align*}| \eta | ^{k} = | \eta^{k} | = | \sum_{i=0}^{k-1} c_i \eta^i | \leq \sum_{i=0}^{k-1} c_i |\eta|^ i.\end{align*} $$

Equality holds in the above if and only if (1) $\eta ^i$ is a nonnegative real for all i for which $c_i \neq 0$ , and (2) $|\eta |$ is a root of P. By Lemma 2.1, the first condition is equivalent to $\eta ^g$ being a nonnegative real, where $g = \gcd \{i \ \lvert \ c_i \neq 0 \}$ . The second condition is equivalent to $|\eta | = \varphi $ , since $|\eta |$ is a nonnegative real. The root $\varphi $ satisfies these conditions, and the other solutions are obtained as the product of $\varphi $ with the gth roots of unity.

If the inequality is strict then we have $P(|\eta |) < 0$ . Since the value of the polynomial $P(|z|)$ is positive for sufficiently large $|z|$ , and $\varphi $ is the unique positive real root, $P(|z|)>0$ for any $|z|>\varphi $ . It follows that $|\eta | < \varphi $ , as required.

For a polynomial $P(z)$ of degree k, let $\eta _1, \dots , \eta _k$ be the roots of P, with multiplicity. The Nth Newton sum of P is the complex number $\eta _1^N+ \dots + \eta _k^N$ . If P has real coefficients, then the roots occur in conjugate pairs and the Newton sums take real values. Lemma 2.2 controls the Newton sums quite tightly. In particular, the next lemma explains that when $N=gn$ is g-divisible they are well approximated asymptotically by $g \varphi ^{gn}$ , and when N is not g-divisible they are approximated by zero with the same error.

Lemma 2.3 Let $c_0, \dots , c_{k-1} \in \mathbb {Z}_{\geq 0}$ , with $c_0 \geq 1$ . Let $\eta _1, \dots , \eta _k$ be the complex roots of the polynomial

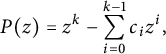$$ \begin{align*}P(z) = z^{k} - \sum_{i=0}^{k-1} c_i z^i,\end{align*} $$

with multiplicity. As $N \to \infty $ , the Newton sums of $P(z)$ satisfy:

• • For N not divisible by g we have

  $$ \begin{align*}\lvert \eta_1^{N} + \dots + \eta_k^{N} \rvert \leq (k-g)|\psi|^{N}.\end{align*} $$

• • When $N=gn$ is g-divisible we have

  $$ \begin{align*}\lvert g \varphi^{gn} - (\eta_1^{gn} + \dots + \eta_k^{gn}) \rvert \leq (k-g)|\psi|^{gn},\end{align*} $$

where $\varphi $ is the unique positive real root of $P(z)$ , $\psi $ is the second largest root in absolute value, and $g=\gcd (\{i \mid c_i \neq 0\}\cup \{k\})$ .

By definition, $|\psi | < \varphi $ . This means that this lemma implies for example that $(\eta _1^{gn} + \dots + \eta _k^{gn}) \sim g \varphi ^{gn}$ as $n \to \infty $ .

Proof By Lemma 2.2, roots of $P(z)$ come in two kinds: those which are the product of $\varphi $ with a gth root of unity, and those roots $\eta $ with $|\eta | < \varphi $ (hence $|\eta | \leq | \psi |$ ). The important point is that each root of the first kind occurs with multiplicity precisely 1.

To see this, apply Lemma 2.2 to the polynomial

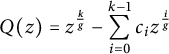$$ \begin{align*}Q(z) = z^{\frac{k}{g}} - \sum_{i=0}^{k-1} c_i z^{\frac{i}{g}}\end{align*} $$

obtained by dividing all powers by g, and use the fact that roots of $P(z)$ are precisely the gth roots of the roots of $Q(z)$ .

Then, without loss of generality assume $\eta _1$ , …, $\eta _g$ are the roots of the first kind, so that $\lvert \eta _1 \rvert = \dots = \lvert \eta _g \rvert = \varphi $ . From elementary complex analysis or group theory, we have that $\eta _1^N + \dots + \eta _g^N = \begin {cases} g \varphi ^N, & g \mid N, \\ 0, & g \nmid N, \end {cases}$ and the result then follows from the triangle inequality.

2.2 Free Lie algebras

We write the generating set X of a free Lie algebra $L=L(X)$ over $\mathbb {Z}$ as follows. Write $q_1 < \dots < q_\ell $ for the distinct degrees which contain an element of X. Write $x_{i,1}, x_{i,2}, \dots , x_{i,m_i}$ for the distinct generators in degree $q_i$ , so that in particular, the number of generators in degree $q_i$ is $m_i$ . Hilton [Hil] showed that L is free as a $\mathbb {Z}$ -module.

Let $\mu : \mathbb {Z}_{> 0} \longrightarrow \{-1, 0, 1\}$ be the Möbius inversion function, defined by

$$ \begin{align*}\mu(s) = \begin{cases} 1, & s=1, \\ 0, & s>1 \textrm{ is not square-free,} \\ (-1)^{\ell}, & s>1 \textrm{ is a product of } \ell \textrm{ distinct primes.} \end{cases}\end{align*} $$

Given a polynomial $P(z) = a_0 + a_1 z + \dots + a_k z^k$ with $ a_0\neq 0$ , the reciprocal of $P(z)$ is $a_k + a_{k-1} z + \dots + a_0 z^k$ . For given $P(z)$ , let $\eta _1, \dots , \eta _k$ be the complex roots of the reciprocal of $P(z)$ , with multiplicity (so $P(z)=a_0 \prod _{i=1}^k (1-\eta _i z)$ ). Write

$$ \begin{align*}S_{N}(P(z)):=\eta_1^N + \dots + \eta_k^N\end{align*} $$

for the Nth Newton sum in the zeros of the reciprocal.

The following theorem is due to Babenko. Relative to his statement, we have changed variable using the fact that, for fixed N, $d \mapsto \frac {N}{d}$ is a self-bijection of the set of divisors of N.

Theorem 2.4 [Bab, Proposition 1]

Let L be the free graded Lie algebra over $\mathbb {Z}$ on a finite set of generators $\{x_{i,j}\}$ , with notation as above. Then

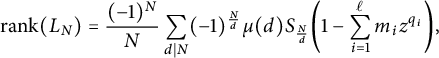$$ \begin{align*} \mathrm{rank}(L_N)=\frac{(-1)^N}{N} \sum_{d \mid N} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}\bigg(1- \sum_{i=1}^{\ell} m_i z^{q_i}\bigg), \end{align*} $$

where the sum is taken over the divisors d of N.

Our next theorem is essentially a result of Lambrechts [Lam, Proposition 1] in the special case of free Lie algebras. Our derivation of this result from Babenko’s is essentially the same as Lambrechts’s, but the situation is simpler and slightly more is true. The point of the theorem is that when $g \mid N$ , $\mathrm{rank}(L_N)$ is well-approximated by $\frac {g}{N} \varphi ^{N}$ with an error term given by a sum of exponentials in smaller bases.

Theorem 2.5 Let L be the free graded Lie algebra over $\mathbb {Z}$ on a finite set of generators X. As before, write $q_1 < \dots < q_\ell $ for the distinct degrees which contain an element of X, and let $g= \gcd (q_i)$ . Let $m_i$ be the number of generators in degree $q_i$ .

• • If $g \nmid N$ , then $\mathrm{rank}(L_N) = 0$ .

• • If $g \mid N$ , then $\lvert \mathrm{rank}(L_N) - \frac {g}{N} \varphi ^{N} \rvert \leq \frac {q_{\ell }}{N}|\psi |^{N}+g \varphi ^{\frac {N}{2}}+q_{\ell }|\psi |^{\frac {N}{2}}$ ,

where $\varphi $ is the unique positive real root of the degree $q_\ell $ polynomial

$$ \begin{align*}P(z)=z^{q_{\ell}} - \sum_{i=1}^\ell m_i z^{q_\ell - q_i} = 0,\end{align*} $$

and $\psi $ is the second largest root in absolute value. In particular, $\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }}$ .

If $P(z)$ has no roots which are strictly smaller than $\varphi $ in absolute value (i.e., “ $\psi $ does not exist”) then terms involving $\psi $ may be disregarded: precisely, the inequality in the second claim may be replaced by $\lvert \mathrm{rank}(L_N) - \frac {g}{N} \varphi ^{N} \rvert \leq g \varphi ^{\frac {N}{2}}$ .

Proof The first claim follows immediately from the fact that L is concentrated in degrees divisible by g.

We will now prove the second claim. The point is that the Babenko’s formula of Theorem 2.4 is dominated by the $d=1$ term. Let N be divisible by g. By Theorem 2.4 (using that $\mu (1)=1$ ), we have

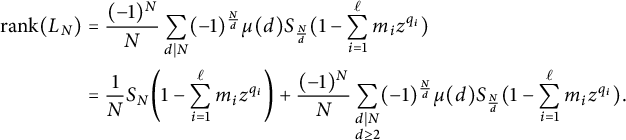$$ \begin{align*} \begin{aligned} \mathrm{rank}(L_N) &=\frac{(-1)^N}{N} \sum_{d \mid N} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}(1- \sum_{i=1}^{\ell} m_i z^{q_i}) \\ &= \frac{1}{N}S_{N}\bigg(1- \sum_{i=1}^{\ell} m_i z^{q_i}\bigg) + \frac{(-1)^N}{N} \sum_{\substack{d \mid N \\ d \geq 2}} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}(1- \sum_{i=1}^{\ell} m_i z^{q_i}). \end{aligned} \end{align*} $$

We name these two terms, writing $S_N=S_{N}(1- \sum _{i=1}^{\ell } m_i z^{q_i})$ to simplify notation. Let

$$ \begin{align*}A_N := \frac{1}{N}S_{N},\end{align*} $$

and let

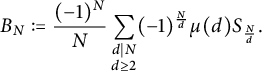$$ \begin{align*}B_N := \frac{(-1)^N}{N} \sum_{\substack{d \mid N \\ d \geq 2}} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}}.\end{align*} $$

By Lemma 2.3 (with $n = \frac {N}{g}$ ), we have $\lvert S_N - g \varphi ^{N} \rvert \leq (q_\ell - g) |\psi |^N \leq q_\ell |\psi |^N$ for $\varphi $ and $\psi $ as in the theorem statement. It therefore suffices to show that $\lvert B_N \rvert \leq g \varphi ^{\frac {N}{2}} + q_{\ell }|\psi |^{\frac {N}{2}}.$

Since $\lvert \mu (d) \rvert \leq 1$ , we have by Lemma 2.3 that

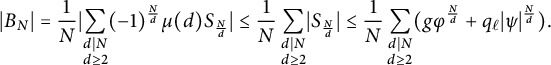$$ \begin{align*}\lvert B_N \rvert = \frac{1}{N} \lvert \sum_{\substack{d \mid N \\ d \geq 2}} (-1)^{\frac{N}{d}} \mu(d) S_{\frac{N}{d}} \rvert \leq \frac{1}{N} \sum_{\substack{d \mid N \\ d \geq 2}} \lvert S_{\frac{N}{d}} \rvert \leq \frac{1}{N} \sum_{\substack{d \mid N \\ d \geq 2}}( g \varphi^{\frac{N}{d}} + q_{\ell}|\psi|^{\frac{N}{d}}).\end{align*} $$

The number of terms in this summation is at most the number of divisors of N, which is at most N. The term is a sum of exponentials in positive bases, hence is strictly increasing, and in particular, for $d \geq 2,$ we have the termwise bound $g \varphi ^{\frac {N}{d}} + q_{\ell }|\psi |^{\frac {N}{d}} \leq g \varphi ^{\frac {N}{2}} + q_{\ell }|\psi |^{\frac {N}{2}}$ . Putting this together gives

$$ \begin{align*}\lvert B_N \rvert \leq g \varphi^{\frac{N}{2}} + q_{\ell}|\psi|^{\frac{N}{2}},\end{align*} $$

as required.

Lastly, we check that $\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }}$ . Since the polynomial $P(z) = z^{q_{\ell }} - \sum _{i=1}^\ell m_i z^{q_\ell - q_i}$ has a unique positive root by Lemma 2.2, it suffices to check that $P((\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }})$ is nonpositive. For each i, $\frac {q_\ell - q_i}{q_\ell }$ lies between 1 and 0, so for any $x \geq 1,$ we have $x^{\frac {q_\ell - q_i}{q_\ell }} \geq 1$ . It follows that

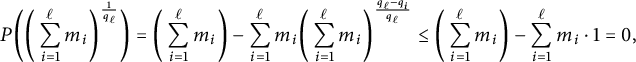$$ \begin{align*} P\bigg(\bigg(\sum_{i=1}^\ell m_i\bigg)^{\frac{1}{q_\ell}}\bigg) = \bigg(\sum_{i=1}^\ell m_i\bigg) - \sum_{i=1}^\ell m_i \bigg(\sum_{i=1}^\ell m_i\bigg)^{\frac{q_\ell - q_i}{q_\ell}} \leq \bigg(\sum_{i=1}^\ell m_i\bigg) - \sum_{i=1}^\ell m_i \cdot 1 = 0, \end{align*} $$

as required.

2.3 Free Lie algebras with differentials

Free Lie algebras over ${\mathbb {Z}/p^r}$ are obtained by tensoring the corresponding free Lie algebra over $\mathbb {Z}$ with ${\mathbb {Z}/p^r}$ , since this gives the correct universal property.

In this subsection, we consider $L=L(x,y)=L(x,dx)$ , the free differential Lie algebra over ${\mathbb {Z}/p^r}$ on the acyclic rank 2 free differential ${\mathbb {Z}/p^r}$ -module on generators x and y ( $dx = y$ ). Suppose that $\deg (x)=q+1$ , so $\deg (y)=q$ . By Theorem 2.5, since $\gcd (q,q+1)=1$ , we know that

$$ \begin{align*}\mathrm{rank}_{{\mathbb{Z}/p^r}}(L_N) \sim \frac{1}{N} \varphi^{N},\end{align*} $$

where $\varphi $ is the unique positive real root of the degree $q+1$ polynomial

$$ \begin{align*}z^{q+1}-z-1 = 0.\end{align*} $$

The size of the error in this approximation is exponential in base depending on the second largest root $\psi $ (in absolute value), and $\sqrt {\varphi }$ .

In this subsection, we are instead interested in $B := \textrm {Im}(d) \subset L$ , the module of boundaries. Our aim is to prove Theorem 2.11. The argument will go as follows. It is known (Theorem 2.7) that the differential on L is “almost acyclic.” A counting argument using the fact that $\mathrm{rank}(L_N) \sim \frac {1}{N} \varphi ^{N}$ then shows that the rank of the module of boundaries must be asymptotically a fixed fraction of that of $L_N$ .

We will first reduce to the case $r=1$ by means of the following lemma, which is proven in [Boy2] as Lemma 7.10.

Lemma 2.6 Let $\varphi : M \longrightarrow N$ be a map of ${\mathbb {Z}/p^r}$ -modules, with N free. Then $\mathrm{rank}_{{\mathbb {Z}/p^r}}(\mathrm {Im}(\varphi )) = \mathrm{rank}_{{\mathbb {Z}/p}}(\mathrm {Im}(\varphi \otimes {\mathbb {Z}/p}))$ .

Now assume $r=1$ . Let u be an even-dimensional class in a graded differential Lie algebra L over ${\mathbb {Z}/p}$ for $p \neq 2$ . Following [CMN], let

$$ \begin{align*}\tau_k(u) = \mathrm{ad}^{p^k-1}(u)(du),\end{align*} $$

and let

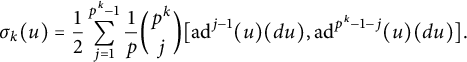$$ \begin{align*}\sigma_k(u) = \frac{1}{2} \sum_{j=1}^{p^k-1} \frac{1}{p}{p^k \choose j}[\mathrm{ad}^{j-1}(u)(du), \mathrm{ad}^{p^k-1-j}(u)(du)].\end{align*} $$

From our point of view, the point of the next theorem is that free differential Lie algebras are almost acyclic.

Theorem 2.7 [CMN, Proposition 4.9]

Let V be an acyclic differential ${\mathbb {Z}/p}$ -vector space. Write $L(V) \cong HL(V) \oplus K$ , for an acyclic module K. If K has an acyclic basis, that is, a basis

$$ \begin{align*}\{x_\alpha, y_\alpha, z_\beta, w_\beta\},\end{align*} $$

where $\alpha $ and $\beta $ range over index sets $\mathscr {I}$ and $\mathscr {J}$ , respectively, and we have

$$ \begin{align*}d(x_\alpha) = y_\alpha, \mathrm{ deg}(x_\alpha) \textrm{ even,}\end{align*} $$

$$ \begin{align*}d(z_\beta) = w_\beta, \mathrm{ deg}(z_\beta) \textrm{ odd,} \end{align*} $$

then $HL(V)$ has a basis

$$\begin{align*} \{\tau_k(x_\alpha), \sigma_k(x_\alpha)\}_{\alpha \in \mathscr{I}, k \geq 1}. \end{align*}$$

The theorem implies that the differential on L can be modified slightly to make it acyclic. Namely, define a new differential $\overline {d} : L(V) \to L(V)$ by setting $\overline {d} = d$ on K, and letting $\overline {d}(\tau _k(x_\alpha )) = \sigma _k(x_\alpha )$ , $\overline {d}(\sigma _k(x_\alpha )) = 0$ . Of course, $\overline {d}$ will no longer satisfy the Leibniz rule, but it will still be a vector space endomorphism of degree $-1$ which satisfies $\overline {d}^2=0$ .

Now, let $\overline {B} := \mathrm {Im}(\overline {d}) \subset L$ , and let $\sigma \subset L$ be the subspace spanned by the elements $\sigma _k(x)$ , for some even degree $x \in L$ and $k \in \mathbb {Z}^+$ . By definition of $\overline {d}$ , we then have the following corollary.

Corollary 2.8 We have $\overline {B}_N \cong B_N \oplus \sigma _N$ .

The next lemma justifies the approximation by providing a crude upper bound on $\sigma _N$ .

Lemma 2.9 We have the bound

$$ \begin{align*}\dim_{{\mathbb{Z}/p}} \sigma_N \leq c_1 \cdot N \varphi^{\frac{N}{p}},\end{align*} $$

where $c_1 = 2(q+2)\varphi ^{\frac {2}{p}}$ .

Proof By definition, $\sigma _N$ is spanned by classes $\sigma _k(x_\alpha )$ , and we have $\deg (\sigma _k(x_\alpha )) = p^k \deg (x_\alpha )-2$ . We therefore have

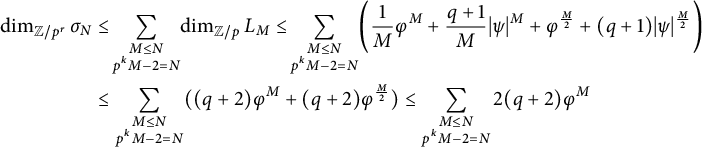$$ \begin{align*} \dim_{{\mathbb{Z}/p^r}} \sigma_N &\leq \!\sum_{\substack{M \leq N \\ p^k M - 2 =N}}\! \dim_{{\mathbb{Z}/p}} L_M \leq \!\sum_{\substack{M \leq N \\ p^k M - 2 =N}} \!\bigg(\frac{1}{M} \varphi^M + \frac{q+1}{M} |\psi|^{M} + \varphi^{\frac{M}{2}} + (q+1)|\psi|^{\frac{M}{2}}\bigg)\\&\leq \sum_{\substack{M \leq N \\ p^k M - 2 =N}} ( (q+2) \varphi^{M} +(q+2)\varphi^{\frac{M}{2}}) \leq \sum_{\substack{M \leq N \\ p^k M - 2 =N}} 2(q+2) \varphi^{M} \end{align*} $$

by Theorem 2.5 (we use $|\psi | < \varphi $ , and then drop the factors of $\frac {1}{M}$ , to obtain a bound which is strictly increasing even for small M). This summation contains fewer than N terms, and since the value of a given term is increasing in M, the size of the largest term is controlled by $M = \frac {N+2}{p^k} \leq \frac {N+2}{p}$ , so

$$ \begin{align*} \dim_{{\mathbb{Z}/p}} \sigma_N \leq N \cdot 2(q+2) \varphi^{\frac{N+2}{p}}, \end{align*} $$

as required.

We next estimate the size of $\dim \overline {B}_N$ .

Lemma 2.10 Let $\psi $ be the second largest (in absolute value) root of $z^{q+1}-z-1$ after $\varphi $ . We have

$$ \begin{align*} \dim_{{\mathbb{Z}/p}} \overline{B}_N \geq (1-\frac{N}{N-1} \frac{1}{\varphi}) \cdot \frac{1}{N} \varphi^N - \kappa \lvert \psi \rvert^N - c_2 \varphi^{\frac{N}{2}}, \end{align*} $$

where $\kappa = (q+1)(1+ \frac {1}{\lvert \psi \rvert })$ and $c_2 = (q+2)(1+ \frac {1}{\sqrt {\varphi }}) \leq 2(q+2)$ .

Proof Since $\overline {d}$ is acyclic, we have $\overline {B}_N = \mathrm {Ker}(\overline {d}: L_N \to L_{N-1})$ . The First Isomorphism Theorem then gives that , and since $\overline {B}_{N-1} \subset L_{N-1}$ , we get

$$ \begin{align*}\dim_{{\mathbb{Z}/p}} \overline{B}_N \geq \dim_{{\mathbb{Z}/p}} L_N - \dim_{{\mathbb{Z}/p}}L_{N-1}.\end{align*} $$

Theorem 2.5 gives (since $g=1$ and $|\psi | < \varphi $ )

$$ \begin{align*} \dim_{{\mathbb{Z}/p}}L_{N-1} \leq \frac{1}{N-1}\varphi^{N-1} + \frac{q+1}{N-1} \lvert \psi \rvert^{N-1} + (q+2) \varphi^{\frac{N-1}{2}}, \end{align*} $$

and

$$ \begin{align*} \dim_{{\mathbb{Z}/p}}L_{N} \geq \frac{1}{N}\varphi^{N} - \frac{q+1}{N} \lvert \psi \rvert^{N} - (q+2)\varphi^{\frac{N}{2}}. \end{align*} $$

Combining these inequalities gives the result.

We are now ready to state and prove the main theorem of this subsection.

Theorem 2.11 Let $L \otimes {\mathbb {Z}/p^r}$ be the free differential graded Lie algebra over ${\mathbb {Z}/p^r}$ on two generators x and y satisfying $y= d x$ . Let $q = \deg (y)$ , so that $\deg (x) = q+1$ . Let $B = \textrm {Im} (d) \subset L \otimes {\mathbb {Z}/p^r}$ be the submodule of boundaries. Then we have the bound

$$ \begin{align*}\mathrm{rank}(B_N) \geq (1 - \frac{N}{N-1} \frac{1}{\varphi}) \cdot \frac{1}{N} \varphi^{N} - c N \varphi^{\frac{N}{2}} - \kappa \lvert \psi \rvert^N, \end{align*} $$

where $\varphi> 1$ is the unique positive real root of the degree n polynomial

$$ \begin{align*} z^{q+1} - z - 1 = 0, \end{align*} $$

$\psi $ is the second largest root in absolute value, $c= 2(q+2)(1+ \varphi )$ , and $\kappa = (q+1)(1+ \frac {1}{\lvert \psi \rvert })$ . We have the bounds $2^{\frac {1}{q+1}}< \varphi < 1 + \frac {1}{q}$ .

Proof By Lemma 2.6, it suffices to prove the theorem in the case $r=1$ . By Lemma 2.8, we have

$$ \begin{align*} \dim_{{\mathbb{Z}/p}} B_N \geq \dim_{{\mathbb{Z}/p}} \overline{B}_N - \dim_{{\mathbb{Z}/p}} \sigma_N. \end{align*} $$

Combining Lemmas 2.9 and 2.10 ( $c=c_1+c_2$ ) then gives the result.

3 Topology

3.1 Homology

We now prove Theorem 1.2.

Proof of Theorem 1.2

In the proof of Theorem 1.5 of [Boy2] it is shown that there exists a commutative diagram (the details of the definitions of the maps need not concern us here):

In the diagram, $L(x,dx) \otimes {\mathbb {Z}/p^s}$ is the free differential Lie algebra (with $dx=y$ , $\deg (x) = q+1$ , $\deg (y) = q$ ). The top-left entry $L'(x,dx)$ is a certain module over ${\mathbb {Z}/p^r}$ which is “almost” a free differential Lie algebra.

We now use various results from [Boy2]. By the remark immediately before Corollary 8.9 of that paper, the image of the left-hand vertical map $\theta \circ d$ is precisely the module of boundaries $BL$ . By Lemma 9.6, the map $\Phi _H^{r,s}$ is an injection, and the induced map on homology, $(\Omega \mu )_*$ , is an injection by assumption. It follows by commutativity that the image in the bottom-right, $I := \mathrm {Im}(h \circ \rho ^s \circ (\Omega \mu )_* \circ \beta ^r \circ \Phi _\pi ^{r,r})$ , is isomorphic to $BL$ .

The point is then that the homotopy groups of Y surject onto I, hence must be just as large. More precisely, we obtain that

$$ \begin{align*}\sum_{t=s}^r \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_N(\Omega Y)) \geq \mathrm{rank}_{{\mathbb{Z}/p^s}}(I_N) = \mathrm{rank}_{{\mathbb{Z}/p^s}}(BL_N)\end{align*} $$

by Lemma 7.8 of [Boy2] applied to the part of the diagram consisting of

The loops on Y is just a degree shift on homotopy groups, so the result follows by Theorem 2.11 of this paper.

3.2 K-theory

In this subsection, the following linear inequality relating integers j and N will arise often. We will refer to it as Condition (*). Here, X is a fixed space, $\mathrm {conn}(X)$ is the p-local connectivity of X, and $\dim (X)$ is the largest d for which $H^d(X; \mathbb {Q}) \neq 0$ .

(*) $$ \begin{align} j> \frac{1}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}-1\right)N+\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}\right)(\mathrm{conn}(X)+2)-1). \end{align} $$

The next theorem refines and slightly generalizes Theorem 1.4 of [Boy1].

Theorem 3.1 Let p be an odd prime, and let X be a path connected space having the p-local homotopy type of a finite $CW$ -complex. Suppose that there exists a map

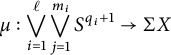$$ \begin{align*}\mu : \bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1} \to \Sigma X\end{align*} $$

with $1 \leq q_1 < q_2 < \dots < q_\ell $ , such that the map

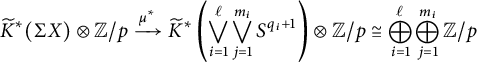$$ \begin{align*}\widetilde{K}^*(\Sigma X) \otimes {\mathbb{Z}/p} \xrightarrow{\mu^*} \widetilde{K}^*\left(\bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1}\right) \otimes {\mathbb{Z}/p} \cong \bigoplus_{i=1}^\ell \bigoplus_{j=1}^{m_i} {\mathbb{Z}/p}\end{align*} $$

is a surjection.

Then, for any N, j such that

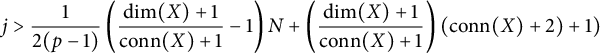$$ \begin{align*}j> \frac{1}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}-1\right)N+\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}\right)(\mathrm{conn}(X)+2)+1)\end{align*} $$

(i.e., such that Condition (*) holds) we have

$$ \begin{align*}\sum_{t=1}^\infty \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{N+2j(p-1)-1}(\Omega \Sigma X)) \geq \mathrm{rank}_{{\mathbb{Z}/p^r}}(L_N \otimes {\mathbb{Z}/p^r}),\end{align*} $$

where L is as in Theorem 2.5 (the free Lie algebra on generators corresponding to the spheres in the wedge), $\mathrm {conn}(X)$ is the p-local connectivity of X, $\dim (X)$ is the dimension of X as measured by rational cohomology, and $g=\gcd (q_1, \dots , q_\ell )$ .

Proof This is essentially a more careful restatement of Theorem 1.4 of [Boy1]. Some of the arguments of that paper are given only for a wedge of two spheres, but all of them apply verbatim to any finite wedge. Construction 7.15 of that paper gives (in slightly different language) a diagram of the form

for some module $E_*$ whose definition need not concern us.

Theorem 7.16 of that paper then says that the horizontal map is an injection, and hence, just as in the proof of Theorem 1.2, the conclusion holds, provided that there exists some $\ell \in \mathbb {Z}_{\geq 0}$ such that $\ell ^{j(p-1)+\frac {N-1}{2}}> \lambda _\ell ^k$ , for an integer k which may be taken to be $\lceil \frac {N+1}{\mathrm{{conn}(X)+1}} \rceil $ , where $\lambda _\ell $ is the largest eigenvalue of the Adams operation $\psi ^\ell $ on $\widetilde {K}^*(X)$ .

The inequality therefore rearranges to $j> \frac {1}{p-1}\left(\lceil \frac {N+1}{\mathrm{{conn}(X)+1}} \rceil \frac {\log (\lambda _\ell )}{\log (\ell )}- \frac {N-1}{2}\right).$ In [AA], it is shown that $\lambda _\ell = \ell ^{\lceil \frac {\dim (X)}{2} \rceil }$ , so we may simplify to

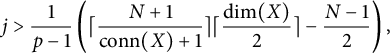$$ \begin{align*}j> \frac{1}{p-1}\left(\lceil \frac{N+1}{\mathrm{conn}(X)+1} \rceil \lceil \frac{\dim(X)}{2} \rceil - \frac{N-1}{2}\right),\end{align*} $$

which is implied by Condition (*), using the fact that, for an integer $z,$ we have $\lceil \frac {z}{2}\rceil \leq \frac {z+1}{2}$ . This completes the proof.

The next step is a simple application of Bezout’s Lemma.

Lemma 3.2 Let $\alpha , \beta \in \mathbb {Z}$ with $\alpha , \beta> 0$ , and let $a,b \in \mathbb {R}$ with $a>0$ . Consider the set of linear combinations

$$ \begin{align*}S_n=\{n \alpha + j \beta \ \mid \ j \in \mathbb{Z}_{\geq 0}, \ j> an+b \} \subset \mathbb{Z}.\end{align*} $$

Let $g' = \gcd (\alpha , \beta )$ . There exists a constant B, independent of n, such that for each n, all multiples of $g'$ which are at least $\min (S_n)+B$ are contained in $S_i$ for some i which is close to n in the sense that $n \leq i < n+\beta (\beta + 1)$ . Furthermore, there exists a suitable B satisfying the bound $B \leq \beta ^2 (\alpha + a (1 + \beta ))+ \beta $ , and hence, any $B \geq \beta ^2 (\alpha + a (1 + \beta )) + \beta $ is also suitable.

If $\alpha $ and $\beta $ are fixed (and j and n are allowed to vary), then it is a familiar fact that the set of integers of the form $n \alpha + j \beta $ is precisely the multiples of $g'$ . Our statement is essentially just a more complicated version of this.

Proof First, consider the set $S_n$ . If an integer j satisfies $j> an+b$ (so that $n \alpha + j \beta $ lies in $S_n$ ), then increasing the parameter j certainly does not violate this condition. Therefore, adding a positive multiple of $\beta $ to an element of $S_n$ yields another element of $S_n$ . In particular, $S_n$ already contains all integers which are obtained by increasing $\min (S_n)$ by a multiple of $\beta $ . These values are by construction linear combinations of $\alpha $ and $\beta $ , so they are all multiples of $g'$ .

It remains, then, to show that by increasing n “just a little,” we can “fill in” the intermediate multiples of $g'$ . We will do so by “giving ourselves enough room,” in the sense of an ad-hoc quantity which we now define. Define the excess of $(j,n)$ to be $j - (an+b)$ . The condition $j> an+b$ is then equivalent to $(j,n)$ having positive excess.

By Bezout’s Lemma, let $x> 0 $ and $y \geq 0$ be the solution of $x \alpha - y \beta = g'$ with smallest nonnegative y. We have $0 < x \leq \frac {g'}{\alpha }+ \beta $ and $0 \leq y \leq \alpha $ . Given an expression $n \alpha + j \beta $ , replacing n by $n+x$ and j by $j-y$ increases the value of the linear combination $n \alpha + j \beta $ by $g'$ , and reduces the excess by the constant $ax+y$ . We will use this to fill in the remaining multiples of $g'$ .

Let $j_0$ realize the smallest member of $S_n$ , in the sense that $\min (S_n) = n \alpha + j_0 \beta $ . Now, take any $j \geq j_0 + \frac {\beta }{g'}(ax+y)$ . The excess of $(n,j_0)$ was positive, so the excess of $(n,j)$ is greater than $\frac {\beta }{g'}(ax+y)$ . We may therefore add $(x,-y)$ to $(n,j)$ up to $\frac {\beta }{g'}$ times while retaining a positive excess (and keeping j nonnegative). This shows that all multiples of $g'$ lying between $n \alpha + j \beta $ and $n \alpha + (j+1) \beta $ are contained in $S_i$ for some i satisfying $n \leq i < n+ \frac {\beta }{g'} x$ , and we may perform this procedure for any $j \geq j_0 + \frac {\beta }{g'}(ax+y)$ . In particular, all multiples of $g'$ which are at least $\min (S_n)+\beta (\frac {\beta }{g'}(ax+y)+1)$ are contained in $S_i$ for some i satisfying $n \leq i < n+ \frac {\beta }{g'} x$ . The extra $+1$ here is because j must be an integer. This is essentially the result, and it remains only to establish that we may take the constants as in the statement.

Now, $\frac {g'}{\alpha } \leq 1$ , so $x \leq 1 + \beta $ , and $\frac {\beta }{g'}x \leq \beta x \leq \beta (1+ \beta )$ . This establishes the bounds on i. The bound on B follows from these inequalities, together with $y \leq \alpha $ . This completes the proof.

We now prove the following strong version of Theorem 1.7.

Theorem 3.3 Let p be an odd prime, and let X be a path connected space having the p-local homotopy type of a finite $CW$ -complex. Suppose that there exists a map

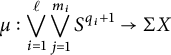$$ \begin{align*}\mu : \bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1} \to \Sigma X\end{align*} $$

with $1 \leq q_1 < q_2 < \dots < q_\ell $ , such that the map

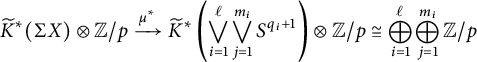$$ \begin{align*}\widetilde{K}^*(\Sigma X) \otimes {\mathbb{Z}/p} \xrightarrow{\mu^*} \widetilde{K}^*\left(\bigvee_{i=1}^\ell \bigvee_{j=1}^{m_i} S^{q_i+1}\right) \otimes {\mathbb{Z}/p} \cong \bigoplus_{i=1}^\ell \bigoplus_{j=1}^{m_i} {\mathbb{Z}/p}\end{align*} $$

is a surjection.

Then there exist constants $\tau ,\theta>0$ such that for multiples $M=mg'$ of

$$ \begin{align*}g'=\gcd(q_1, \dots, q_\ell,2(p-1)),\end{align*} $$

we have

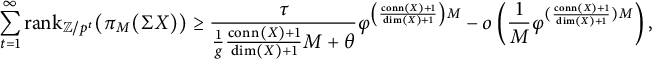$$ \begin{align*}\sum_{t=1}^\infty \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{M}(\Sigma X))\geq \frac{\tau}{\frac{1}{g}\frac{\mathrm{conn}(X)+1}{\dim(X)+1}M + \theta} \varphi^{\left(\frac{\mathrm{conn}(X)+1}{\dim(X)+1}\right)M}-o\left(\frac{1}{M}\varphi^{(\frac{\mathrm{conn}(X)+1}{\dim(X)+1})M}\right),\end{align*} $$

where $\varphi $ is the unique positive real root of the degree $q_\ell $ polynomial

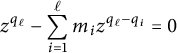$$ \begin{align*}z^{q_\ell} - \sum_{i=1}^\ell m_i z^{q_\ell - q_i} = 0\end{align*} $$

(in particular, $\varphi \geq (\sum _{i=1}^\ell m_i)^{\frac {1}{q_\ell }} = (\sum _{i=1}^\ell m_i)^{\frac {1}{\max (q_1, \dots , q_\ell )}}$ ), $\mathrm {conn}(X)$ is the p-local connectivity of X, $\dim (X)$ is the rational cohomological dimension of X, and $g=\gcd (q_1, \dots , q_\ell )$ .

Proof Let $S_n$ be the set of dimensions M for which Theorem 3.1 tells us that $\sum _{t=1}^\infty \mathrm {rank}_{{\mathbb {Z}/p^t}}(\pi _{M}(\Sigma X)) \geq \dim _{{\mathbb {Z}/p}}(L_{ng} \otimes {\mathbb {Z}/p^r})$ . That is,

$$ \begin{align*}S_n = \{ng+j\cdot 2(p-1) \ \mid \ j \in \mathbb{Z}, \ j> an+b \} \subset \mathbb{Z},\end{align*} $$

where $a=\frac {g}{2(p-1)}\left(\frac {\dim (X)+1}{\mathrm{{conn}(X)+1}}-1\right)$ and $b = \frac {1}{2(p-1)}\left(\frac {\dim (X)+1}{\mathrm{{conn}(X)+1}}(\mathrm {conn}(X)+2)+1\right)$ .

By Lemma 3.2, there exists a constant B, which may be taken to be $4(p-1)^2 (g + a (1 + 2(p-1)))+ 2(p-1)$ such that, for each $M=mg' \geq \min (S_n) + B$ , we have $\sum _{t=1}^\infty \mathrm {rank}_{{\mathbb {Z}/p^t}}(\pi _{M}(\Sigma X)) \geq \dim _{{\mathbb {Z}/p}}(L_{ig} \otimes {\mathbb {Z}/p^r})$ for some i with $n \leq i < n + 8(p-1)^2$ . By Theorem 2.5,

$$ \begin{align*}\sum_{t=1}^\infty \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{M}(\Sigma X)) \geq \frac{1}{i} \varphi^{ig} - q_{\ell}|\psi|^{ig}-g \varphi^{\frac{ig}{2}}-q_{\ell}|\psi|^{\frac{ig}{2}}.\end{align*} $$

Regardless of whether $|\psi |> 1$ , we have $|\psi |^{\frac {ig}{2}} < 1 + |\psi |^{ig} < 2 + |\psi |^{(n+8(p-1)^2)g}$ , so the inequality implies

(†) $$ \begin{align} \sum_{t=1}^\infty \mathrm{rank}_{{\mathbb{Z}/p^t}}(\pi_{M}(\Sigma X)) \geq \frac{1}{n+8(p-1)^2} \varphi^{ng}-g \varphi^{\frac{(n+8(p-1)^2)g}{2}} - q_{\ell}(3+2|\psi|^{(n+8(p-1)^2)g}). \end{align} $$

It remains only to find the dependency of n upon M, and convert this expression into one in terms of M.

The smallest member of $S_n$ is obtained by taking the smallest $j=j_n$ satisfying Condition (*). By definition $j_n$ is the smallest integer with $j_n> an+b$ , so $j_n \leq an+b + 1$ . Thus,

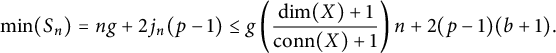$$ \begin{align*}\min(S_n)=ng+2j_n(p-1) \leq g\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}\right)n+2(p-1)(b+1).\end{align*} $$

To conclude, for given $M=mg'$ , let $n=n(M)$ be the largest nonnegative integer satisfying $M \geq g(\frac {\dim (X)+1}{\mathrm{{conn}(X)+1}})n+2(p-1)(b+1)+B$ . Rearranging gives $n \leq \frac {M-(2(p-1)(b+1)+B)}{g} (\frac {\mathrm{{conn}(X)+1}}{\dim (X)+1})$ . Since n is the largest such integer, it is at least one less than this expression. Applying the bounds $n \leq i < n + 8(p-1)^2$ , now gives that

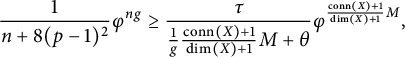$$ \begin{align*}\frac{1}{n+8(p-1)^2} \varphi^{ng} \geq \frac{\tau}{\frac{1}{g}\frac{\mathrm{conn}(X)+1}{\dim(X)+1}M + \theta} \varphi^{\frac{\mathrm{conn}(X)+1}{\dim(X)+1}M},\end{align*} $$

for constants $\theta $ and $\tau $ , and shows that the other terms of the inequality † are $o(\frac {1}{M}\varphi ^{\frac {\mathrm{{conn}(X)+1}}{\dim (X)+1}})$ , as required.

Remark 3.4 In this remark, we give the constants and error term for Theorem 3.3, and collect the other constants appearing in the proof.

The positive integers $q_1, \dots , q_\ell $ are given in the hypotheses of Theorem 3.3 (or Theorem 2.5). Then

$$ \begin{align*}g=\gcd(q_1, \dots , q_\ell),\end{align*} $$

and

$$ \begin{align*}g' = \gcd(q_1, \dots, q_\ell, 2(p-1)) = \gcd(g, 2(p-1)).\end{align*} $$

The space X and the prime $p \neq 2$ are given in the hypotheses of Theorem 3.3, $\dim (X)$ is the rational dimension of X, and $\mathrm {conn}(X)$ is its p-local connectivity.

The constants appearing in the proof of Theorem 3.3 are then

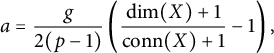$$ \begin{align*}a=\frac{g}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}-1\right),\end{align*} $$

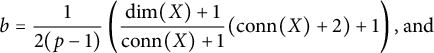$$ \begin{align*}b = \frac{1}{2(p-1)}\left(\frac{\dim(X)+1}{\mathrm{conn}(X)+1}(\mathrm{conn}(X)+2)+1\right) \textrm{, and} \end{align*} $$

$$ \begin{align*}B=4(p-1)^2 (g + a (1 + 2(p-1))) + 2(p-1).\end{align*} $$

It then follows from the proof that the constants $\theta $ and $\tau $ of Theorem 3.3 may be taken as follows:

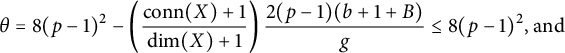$$ \begin{align*}\theta = 8(p-1)^2 - \left(\frac{\mathrm{conn}(X)+1}{\dim(X)+1}\right)\frac{2(p-1)(b+1+B)}{g} \leq 8(p-1)^2 \textrm{, and}\end{align*} $$

$$ \begin{align*}\tau = \varphi^{-g-(\frac{\mathrm{conn}(X)+1}{\dim(X)+1})(2(p-1)(b+1)+B)},\end{align*} $$

where, as usual, $\varphi $ is the unique positive root of the polynomial $P(z) = z^{q_\ell } - \sum _{i=1}^\ell m_i z^{q_\ell - q_i} = 0.$

The error term in the bound Theorem 3.3 is an unpleasant expression, and we restrict ourselves to noting that it is negative, and of the form

$$ \begin{align*}-c_1 \varphi^{\frac{1}{2}\frac{\mathrm{conn}(X)+1}{\dim(X)+1} M} - c_2 |\psi|^{\frac{\mathrm{conn}(X)+1}{\dim(X)+1}M} - 3 q_\ell,\end{align*} $$

for constants $c_i$ , where $\psi $ is the second largest root of $P(z)$ , in absolute value. The deviation of the bound from being a pleasant expression is therefore exponential in bases determined by the roots of $P(z)$ .