Article contents
Nonspecial varieties and generalised Lang–Vojta conjectures
Published online by Cambridge University Press: 10 February 2021
Abstract
We construct a family of fibred threefolds 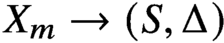 $X_m \to (S , \Delta )$ such that
$X_m \to (S , \Delta )$ such that 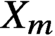 $X_m$ has no étale cover that dominates a variety of general type but it dominates the orbifold
$X_m$ has no étale cover that dominates a variety of general type but it dominates the orbifold 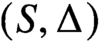 $(S,\Delta )$ of general type. Following Campana, the threefolds
$(S,\Delta )$ of general type. Following Campana, the threefolds 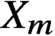 $X_m$ are called weakly special but not special. The Weak Specialness Conjecture predicts that a weakly special variety defined over a number field has a potentially dense set of rational points. We prove that if m is big enough, the threefolds
$X_m$ are called weakly special but not special. The Weak Specialness Conjecture predicts that a weakly special variety defined over a number field has a potentially dense set of rational points. We prove that if m is big enough, the threefolds 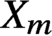 $X_m$ present behaviours that contradict the function field and analytic analogue of the Weak Specialness Conjecture. We prove our results by adapting the recent method of Ru and Vojta. We also formulate some generalisations of known conjectures on exceptional loci that fit into Campana’s program and prove some cases over function fields.
$X_m$ present behaviours that contradict the function field and analytic analogue of the Weak Specialness Conjecture. We prove our results by adapting the recent method of Ru and Vojta. We also formulate some generalisations of known conjectures on exceptional loci that fit into Campana’s program and prove some cases over function fields.
- Type
- Algebraic and Complex Geometry
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
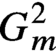 ${G}_m^2$’, Preprint, 2019, arXiv:1911.07562.Google Scholar
${G}_m^2$’, Preprint, 2019, arXiv:1911.07562.Google Scholar ${G}_m^2$ (and integral points on affine subsets of
${G}_m^2$ (and integral points on affine subsets of - 9
- Cited by



