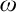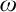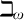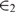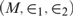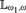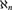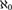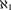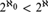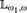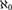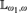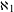12 results
CATEGORICAL QUANTIFICATION
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 24 January 2024, pp. 227-252
- Print publication:
- June 2024
-
- Article
- Export citation

Philosophical Uses of Categoricity Arguments
-
- Published online:
- 02 December 2023
- Print publication:
- 21 December 2023
-
- Element
- Export citation
ON CATEGORICITY IN SUCCESSIVE CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 20 July 2020, pp. 545-563
- Print publication:
- June 2022
-
- Article
- Export citation
AN EXTENSION OF A THEOREM OF ZERMELO
-
- Journal:
- Bulletin of Symbolic Logic / Volume 25 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 06 March 2019, pp. 208-212
- Print publication:
- June 2019
-
- Article
- Export citation
UNIVERSAL CLASSES NEAR
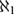 ${\aleph _1}$
${\aleph _1}$
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 21 December 2018, pp. 1633-1643
- Print publication:
- December 2018
-
- Article
- Export citation
UNIVERSAL COVERS OF COMMUTATIVE FINITE MORLEY RANK GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 26 April 2018, pp. 767-799
- Print publication:
- May 2020
-
- Article
- Export citation
FORKING AND SUPERSTABILITY IN TAME AECS
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 09 March 2016, pp. 357-383
- Print publication:
- March 2016
-
- Article
-
- You have access
- Export citation
CATEGORICITY IN QUASIMINIMAL PREGEOMETRY CLASSES
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 56-64
- Print publication:
- March 2016
-
- Article
- Export citation
CATEGORICITY OF MODULAR AND SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 30 September 2015, pp. 1075-1101
- Print publication:
- November 2017
-
- Article
- Export citation
HOMOGENEITY AND FIX-POINTS: GOING FORTH!
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 April 2015, pp. 636-660
- Print publication:
- June 2015
-
- Article
- Export citation
COMPLETENESS AND CATEGORICITY (IN POWER): FORMALIZATION WITHOUT FOUNDATIONALISM*
-
- Journal:
- Bulletin of Symbolic Logic / Volume 20 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 13 May 2014, pp. 39-79
- Print publication:
- March 2014
-
- Article
- Export citation
Uncountable dense categoricity in cats
-
- Journal:
- The Journal of Symbolic Logic / Volume 70 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 12 March 2014, pp. 829-860
- Print publication:
- September 2005
-
- Article
- Export citation