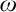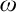CATEGORICAL QUANTIFICATION

Abstract

Due to Gödel’s incompleteness results, the categoricity of a sufficiently rich mathematical theory and the semantic completeness of its underlying logic are two mutually exclusive ideals. For first- and second-order logics we obtain one of them with the cost of losing the other. In addition, in both these logics the rules of deduction for their quantifiers are non-categorical. In this paper I examine two recent arguments—Warren [43] and Murzi and Topey [30]—for the idea that the natural deduction rules for the first-order universal quantifier are categorical, i.e., they uniquely determine its semantic intended meaning. Both of them make use of McGee’s open-endedness requirement and the second one uses in addition Garson’s [19] local models for defining the validity of these rules. I argue that the success of both these arguments is relative to their semantic or infinitary assumptions, which could be easily discharged if the introduction rule for the universal quantifier is taken to be an infinitary rule, i.e., non-compact. Consequently, I reconsider the use of the $\omega $-rule and I show that the addition of the $\omega $-rule to the standard formalizations of first-order logic is categorical. In addition, I argue that the open-endedness requirement does not make the first-order Peano Arithmetic categorical and I advance an argument for its categoricity based on the inferential conservativity requirement.

1 Introduction

Due to Löwenheim–Skolem, completeness, and compactness theorems, the first-order mathematical theories which have an infinite model are non-categorical and, at the same time, due to the results of Carnap [8, 10] and Garson [17, 18], the standard deductive rules for the first-order quantifiers are also non-categorical, since they allow both standard and non-standard models. ¹ If we move to second-order logic, the deductive rules for its quantifiers are still non-categorical, since they allow both standard and Henkin models, but most of the second-order mathematical theories are categorical, if these quantifiers receive their standard meanings. If one prefers having categorical mathematical theories, then second-order logic seems to be a better option, although the cost is losing the semantic completeness with respect to a recursive axiomatization (if $\Gamma \models \phi $ , then $\Gamma \vdash \phi $ ) of the underlying logic of these theories and also the deductive completeness of the theory formalized in this logic ( $T\vdash \phi $ or $T \vdash \sim \phi $ ). If one prefers working in semantically complete first-order logic, then the cost is losing the categoricity of the first-order mathematical theories with infinite models, their deductive completeness, and also the categoricity of the first-order quantifiers. Certainly, depending on one’s goal, a certain logical instrument may be proven to be better that some others. For the present discussion, I assume that semantic completeness and the categoricity of the first-order quantifier rules are valuable properties and, thus, they should be retained.

My aim in this paper is to show that the use of the open-ended natural deduction rules for the first-order universal quantifier and of the local models for defining their validity does not provide the universal quantifier with its unique intended semantic meaning, unless substantial semantic or infinitary assumptions are made. What does this, I argue, is the $\omega $ -rule, whose use provides us in addition with semantic and deductive completeness. The paper is organized as follows: I start by defining the categoricity of a system of logic (Section 2) and then I introduce Carnap’s [8, 10] and Garson’s [17, 18] non-standard valuations for the first-order universal quantifier (Section 3). In Sections 4 and 5, I reconstruct the arguments of Warren [43] and Murzi and Topey [29] based on open-endedness and local models for attaining the categoricity of the first-order universal quantifier and I argue that the success of both these arguments is relative to their semantic or infinitary assumptions. In Section 6, I show that the addition of the $\omega $ -rule to the standard formalizations of first-order logic makes the first-order universal quantifier categorical. Although the use of the $\omega $ -rule also provides us with semantic and deductive completeness, the Löwenheim–Skolem theorem prevents us to obtain the categoricity of the first-order theories without additional constraints. By generalizing the criticism from Sections 4 and 5, I argue (in Section 7) that the open-endedness constraint cannot adequately, i.e., inferentially, fulfil this task. Then I end (Section 8) by advancing an argument for the categoricity of the first-order Peano Arithmetic based on inferential conservativity.

2 The non-categoricity of logic

To formulate the categoricity problem for a system of logic in a more precise way, I will take as primitive the notions of logic and valuation space. ²

Definition 1. A logic L is a set of arguments of the form $\Gamma \vdash \phi $ .

Definition 1.1. If an argument $\Gamma \vdash \phi $ is in L, we say that it is L-valid.

Definition 2. A valuation space V is a class of valuations v, where a valuation v is a function which maps every well-formed formula of the language of L into the set $\{\top , \perp \}$ . $\top $ is the only designated value (truth), while $\perp $ is the only undesignated value (falsehood).

Definition 2.2. A valuation v satisfies an argument $\Gamma \vdash \phi $ if and only if whenever $v(\Gamma )= \top $ , $v(\phi )$ will also be true.

Definition 2.3. If an argument $\Gamma \vdash \phi $ is satisfied by all valuations $v\in V$ , then we say that the argument is V-valid.

Informally, we may say that Definition 1 presents a logic syntactically (or proof-theoretically), since the central notion that it relies on is the syntactic relation of logical consequence (i.e., logical derivability, represented by the sign “ $\vdash $ ”), while Definition 2 presents a logic semantically (or model-theoretically), since the central notion that it relies on is the semantic relation of logical consequence (represented by the sign “ $\models $ ”), which is defined in terms of valuations, i.e., if the argument $\Gamma \vdash \phi $ is satisfied by all valuations $v\in V$ , then $\phi $ is a logical consequence of $\Gamma $ (i.e., $\Gamma \models \phi $ ). The following two definitions (Definitions 3 and 4) will connect these two ways of presenting a system of logic.

Definition 3. $L(V)$ is the set of arguments from L that are V-valid.

Definition 3.1. A valuation v is L-consistent if and only if v satisfies every argument in L.

Definition 3.2. $V(L)$ is the set of valuations v that are L-consistent.

Informally, $L(V)$ is the logic associated with the class of valuations V. For instance, if in V we have the valuations obtained on the basis of the normal truth tables (NTTs) for propositional logic, then $L(V)$ will be the classical propositional calculus in one of its formulations. It can be easily seen that every v from V defined by NTTs is L-consistent in this case, since an argument is V-valid if and only if it is satisfied by each valuation from the space of valuations V. The question which arises at this point is whether the set $V(L)$ contains only the L-consistent valuations which provide the logical terms from L with their standard meanings or whether it also contains L-consistent valuations that provide these logical terms with meanings that are different from the standard ones.

Definition 4. A logic L is categorical if and only if all valuations v from $V(L)$ are standard. ³

At this point we can introduce the logical inferentialist thesis, according to which the formal axioms or rules of inference from a proof-theoretical system of logic determine the meanings of its logical terms. In the terminology introduced above, this thesis states that $L(V)$ uniquely determines the set of L-consistent valuations $V(L)$ such that it contains only standard valuations.

Since the logical inferentialist thesis sets the theoretical framework of the paper, some precisifications of this thesis are thus required. Logical inferentialism is understood in this paper, in line with the other approaches discussed in the sections below, as a model-theoretic inferentialism ([10, 18]), as a metasemantic thesis [43], and as a moderate inferentialism [29]. Model-theoretic inferentialism maintains that the meanings of the logical terms are determined by the formal axioms or rules of inference, but these meanings are to be characterized in model-theoretic terms (such as truth-conditions, denotation, and reference), in opposition to proof-theoretic inferentialism which maintains that the characterization of these meanings should be done in proof-theoretic terms (such as proof and derivability conditions). Logical inferentialism is a metasemantic thesis in the sense that it is primarily concerned with the way in which the logical symbols get their meanings from the rules of inference that govern their use and not with what they mean. For instance, the semantic question concerning the symbol “ $\sim $ ” is what does “ $\sim $ ” mean?, while the metasemantic question is how does “ $\sim $ ” get its meaning from the rules? Logical inferentialism is a moderate form of inferentialism, and not an extreme one, because it does not identify the meanings of the logical symbols with the rules that govern their use, but rather it tries to read off from the rules the model-theoretic meanings of these symbols.

An important presupposition of logical inferentialism thus understood is that the logical terms have a previously given semantics which defines their standard or intended meanings, and the problem is whether we can read off from the formal rules of inference only their standard meanings, or, to express it differently, whether the rules of inference are compatible only with valuations (i.e., L-consistent valuations) that provide these terms with their standard meanings. For instance, it is very easy to read off the meaning of “ $\&$ ” from its introduction and elimination rules. All that we need to assume is that the rules transmit the designated value $\top $ when we pass from the premises to the conclusion, and they retransmit the undesignated value $\perp $ from the conclusion to at least one of the premises, i.e., the rules are sound. In this way, the introduction rule for “ $\&$ ” fixes the first line of the NTT for “ $\&$ ” (if both p and q are $\top $ , then $p\&q$ is $\top $ ), while the elimination rules fix the remaining lines (if p is $\perp $ , then $p\&q$ is $\perp $ ; if q is $\perp $ , then $p\&q$ is $\perp $ ). Since the rules for “ $\&$ ” uniquely fix its standard meaning, there is no non-standard valuation compatible with these rules. ⁴ This result, however, does not also hold for many other logical terms, as we shall see below, in Section 3. For instance, the inference rules for “ $\sim $ ” fix no line from its NTT and, thus, they let open the possibility of a non-standard valuation which assigns the designated value $\top $ both to a sentence and to its negation.

As a matter of historical fact, Carnap [8, p. xv] initially believed that a system of logic could be identified with a set of arguments generated by an arbitrary initial list of formal axioms and rules of inference whose validity is taken to be primitive (his famous principle of tolerance). However, his later engagement in semantics made him impose a first restriction on the arbitrary character of the initial list. Carnap [9, pp. 218–219] argued that when a system of logic L is defined in relation to a semantical system $V(L)$ , this logic has to be formulated with the aim of matching the semantics previously given. This matching requires that all the arguments from L are V-valid (i.e., L is sound), all arguments from $L(V)$ are derivable from the initial list of axioms and rules of inference (i.e., L is semantically complete), and, in addition, all the logical terms from L preserve their intended semantic meanings in all the valuations that are L-consistent (i.e., L is categorical). If all these three conditions are met, then L is a full formalization of the semantical system previously given. Carnap’s [10] discoveries were negative regarding the third condition, in the sense that there are valuations associated with the propositional and first-order standard calculi (i.e., calculi with a finite number of premises and a single conclusion) which are L-consistent, but provide most of the logical terms with non-standard (or non-normal, in Carnap’s terms) meanings. ⁵

3 Carnap’s and Garson’s non-standard valuations for $\forall$

Carnap’s method for proving the non-categoricity of the standard formalizations of propositional and first-order logics (i.e., formalizations with a finite number of premises and a single conclusion) is analogous with Skolem’s [38, 39] method for proving the non-categoricity of Peano Arithmetic, namely, it consists in the construction of a non-standard model. For the propositional calculi L, Carnap [10, 70–94] proved that there are two exclusive kinds of non-standard valuations (non-normal interpretations in Carnap’s terms) and provided two instances of them: one trivial valuation ( $v^{\top }$ ) in which all formulae from L are mapped by $v^{\top }$ to $\top $ , i.e., all sentences are interpreted as true, and the second one (the provability valuation, $v^{\vdash }$ ) in which all and only the theorems from L are mapped by $v^{\vdash }$ to $\top $ , i.e., all and only the theorems are interpreted as true. It can be easily seen that the trivial valuation $v^{\top }$ and the provability valuation $v^{\vdash }$ are L-consistent valuations, since they satisfy all arguments from L, i.e., they produce no counterexamples. Thus, the set $\{v^{\top }\kern-1pt, v^{\vdash }\}$ is a subset of $V(L)$ in the case in which L has the form of one of its standard propositional formalizations, i.e., all its arguments are single conclusion arguments. Thus, according to Definition 4, the standard formalizations of classical propositional logic are non-categorical.

These non-standard valuations $v^{\top }$ and $v^{\vdash }$ arise because the semantic principles of excluded middle and of non-contradiction are not syntactically represented by the standard single-conclusion propositional calculi. More precisely, the semantical concepts of L-exclusive (i.e., a sentence and its negation cannot both be true) and L-disjunct (i.e., a sentence and its negation cannot both be false) are not formalized by these propositional calculi.

In the case of quantificational first-order logic, Carnap observed that, due to the fact that the rules of inference have a finitary character, i.e., they allow only a finite number of premises and conclusions, while a universally quantified sentence can be a semantical consequence of a set of premises without being a semantical consequence of any finite subset of the initial set, a universal sentence is not syntactically (or proof-theoretically) equivalent with its entire set of instances. In other words, there is an asymmetry between logical consequence and logical derivability. Certainly, the universal instantiation/universal elimination rule allows us to pass from a universally quantified sentence to all its (potentially infinite number of) instances, but the universal generalization/universal introduction rule does not allow us to make the opposite move, i.e., $\{\phi [t/x]: t \text { is a term of } L\} \not \vdash (\forall x)\phi x$ . Carnap [8, pp. 231–232], [10, p. 140] thus concluded that we can also construct an L-consistent interpretation in which $(\forall x)\phi x$ is interpreted as “all objects are $\phi $ , and b is $\psi $ ”, where b names an object from the domain. It should be mentioned that Carnap [10, pp. 136–139] worked with the assumption that we have a denumerable infinite domain D, such that all the objects from D are named in the language of L (we may think that this is the domain of a Henkin model), and that the quantifiers could be treated as potentially infinite conjunctions or disjunctions.

The assumption of a denumerable infinite domain such that all objects are named in the language will be preserved throughout the paper. This assumption, however, does not limit the generality of the approach and it is also useful in comparing all the other approaches discussed below. In particular, the generality of the approach is not lost because, due to Löwenheim–Skolem theorem, every satisfiable formula of first-order logic is also satisfiable in a denumerable infinite domain. Likewise, the assumption that every object from the domain is named in the language is logically unproblematic due to Henkin’s [20] technique for building up a canonical model, i.e., a model in which the objects from the domain are the individual constants themselves. Sure, the assumption of nameability erases the distinction between the substitutional and the objectual interpretation of the quantifiers, but in the present context it is unproblematic. This is so because, on the one side, all the domains that are considered are denumerable and, thus, we can use the arithmetical numerals for naming all their objects and, on the other side, the open-endedness condition adopted both by Warren [43] and Murzi and Topey [29] always allows the introduction of individual constants in the expansion of the original language to block the possibility of having unnamed objects. In addition, Garson’s [18, pp. 237–238] also uses Henkin’s [20] method when he considers objectual models that contain variables (or individual constants) in their domains. ⁶

For expressing Carnap’s result in terms of valuations, we may define two valuations: i) a valuation $v'$ which assigns truth to all the instances $\phi _t$ (where t is a term that names an object from D) of $(\forall x)\phi x$ when it assigns truth to $(\forall x)\phi x$ , and ii) a valuation $v^+$ which assigns truth to all the instances $\phi _t$ of $(\forall x)\phi x$ and simultaneously assigns truth to $\psi _b$ (where b is one of the terms t), when it assigns truth to $(\forall x)\phi x$ . Having in mind for the moment the substitutional semantics for the first-order quantifiers, $v'$ is a standard valuation, while $v^+$ is a non-standard valuation. To preserve the duality of the quantifiers, i.e., $(\forall x)\phi x \dashv \vdash \sim (\exists x)\sim \phi x$ , $v^+$ will simultaneously assign truth to $(\exists x)\phi x$ when it assigns truth to at least one of the instances $\phi _t$ or to $\sim \psi _b$ . Thus, since $v^+$ is L-consistent, but provides the quantifiers with meanings different from the standard ones, the standard formalizations of first-order logic are non-categorical (according to Definition 4).

The possibility of the non-standard valuation $v^+$ has a different cause than the non-standard valuations $v^{\top }$ and $v^{\vdash }$ that arise in propositional logic. Thus, $v^+$ is still available even if the valuations $v^{\top }$ , $v^{\vdash }$ are blocked (for instance by using, as Carnap [10] did, a refutation rule which forbids having all sentences interpreted as true and a multiple-conclusion rule for disjunction, which blocks $v^{\vdash }$ ; see also [34, 37, 40]). The non-standard valuation $v^+$ arises because, in the standard formalizations of first-order logic, a universally quantified sentence is not deductively equivalent (C-equivalent, in Carnap’s terms) with the class formed by the conjunction of all the instances of the operand and an existentially quantified sentence is not C-equivalent with the disjunctive class of all the instances of the operand. The deductive implication from the universal sentence to the whole conjunction of its instances is guaranteed by the universal elimination rule and conjunction introduction, but the other standard rules or axioms do not guarantee the converse.

A more elegant example of a non-standard valuation for the universal quantifier has been provided by Garson [17, 18]. I shall not discuss here all the details of Garson’s account, ⁷ but I will come back below (in Section 6) to some of them when the idea of a local model will be introduced. Let us define the standard substitutional $||s\forall ||$ and objectual $||d\forall ||$ semantics for the universal quantifier as follows:

$$ \begin{align*}||s\forall || v(\forall x\phi x)&= \top\text{ iff for all terms }t\text{ in the set of terms }\operatorname{Term}\text{ of }L, v(\phi [t/x])= \top,\\ ||d\forall || v(\forall x\phi x)&= \top\text{ iff for all objects }d\text{ in the domain }D, v(\phi [d/x])= \top.\end{align*} $$

Garson (17, p. 171) ⁸ [18, p. 237] observes that the set $\{\phi [t/x]: t \text { is a term of } L\}\cup \{\sim (\forall x)\phi x\}$ is consistent in first-order logic and, by the Lindenbaum Lemma, we can construct an extension of it which is maximal consistent. ⁹ However, on pain of inconsistency, this extension cannot be omega complete. Thus, we can define a valuation $v^{\omega }$ which assigns $\top $ to each member of $\{\phi [t/x]: t \text { is a term of } L\}$ , but assigns $\perp $ to $(\forall x)\phi x$ . This valuation provides the same result if the objectual semantics is considered and D is taken in this case to be, as in Henkin’s construction, the set of terms of L. This valuation $v^{\omega }$ is L-consistent by definition and thus a member of $V(L)$ , but since it provides the universal quantifier with a meaning different from its standard one, as it is defined by $||s\forall ||$ and $||d\forall ||$ , the standard formalizations of first-order logic are non-categorical. In the following sections I will analyze two recent arguments for restoring the categoricity of the universal quantifier and I will argue that the success of both these arguments is relative to their semantic or infinitary assumptions, which could be easily discharged if the introduction rule for the universal quantifier is taken to be an infinitary rule. In particular, without adding a non-compact infinitary argument $\Gamma \vdash \phi $ in L, or without using an infinitary rule of inference, the valuations $v^+$ and $v^{\omega }$ cannot be blocked only by purely inferential means, i.e., eliminated from $V(L)$ .

4 Warren’s open-endedness argument for restoring categoricity

Warren [43, pp. 85–86] argued that the categoricity of the first-order quantifiers can be restored if the natural deduction rules are taken to be open-ended. ¹⁰ In line with Bonnay and Westerståhl [3], Warren treats the first-order quantifiers as generalized quantifiers, i.e., as properties of properties, and the problem is, thus, to show that the open-endedness of the natural deduction rules guarantees that the only meaning that the universal quantifier receives from its introduction and elimination rules is the standard one. If we consider a non-empty domain D and take “ $\operatorname {Ext}(x)$ ” to denote the extension of a variable “x” in D, by standard Warren means that the extension of the universal quantifier is the entire domain ( $\operatorname {Ext}(x)=D$ iff $\operatorname {Ext}(x)\in \operatorname {Ext}(\forall )$ ). Let us now consider Warren’s [43, pp. 85–86] proof for the categoricity of the open-ended natural deduction rules for the universal quantifier. Since the universal elimination rule is not responsible for the existence of non-standard valuations, I shall consider only the sufficiency direction of the proof: ¹¹

Theorem. $\operatorname {Ext}(x) =D$ iff $\operatorname {Ext}(x)\in \operatorname {Ext}(\forall )$ .

Proof (Sufficiency) Let us assume that $\operatorname {Ext}(x) =D$ and, for reductio, that $\operatorname {Ext}(x)\not \in \operatorname {Ext}(\forall )$ . We add the predicate ‘ $\phi $ ’ to our language such that $\operatorname {Ext}(\phi )= \operatorname {Ext}(x)$ . Let c be an individual constant such that $\operatorname {Ext}(c)=o$ , for some member o of D. We are now in an expanded language where “ $\phi c$ ” is true for some arbitrary ‘c’, but “ $(\forall x)\phi x$ ” is false. This contradicts the open-ended validity of the $\forall $ -introduction rule. Hence, $\operatorname {Ext}(x)\in \operatorname {Ext}(\forall )$ .

For better understanding and referring to the individual steps of the reasoning involved in this proof, I shall reconstruct it in the form of a Lemmon-style natural deduction derivation:

$$\begin{align*}\kern-6pt\begin{array}{llr} \textbf{1} & (1)\ \operatorname{Ext}(x) = D & \hfill\textbf{Premise}\\\textbf{2} & (2)\ \operatorname{Ext}(x)\not\in \operatorname{Ext}(\forall)& \hfill \textbf{Assumption} \\\textbf{3} & (3)\ \text{Let }L\text{ be }L\cup \{\phi\}\text{ such that }\operatorname{Ext}(\phi)= \operatorname{Ext}(x)& \hfill \textbf{Open-endedness}\\\textbf{4} & (4)\ \text{Let }L^{\prime \prime}\text{ be }L\cup \{c\},\text{ such that }\operatorname{Ext}(c)=o,& \hfill \textbf{Open-endedness}\\& \kern18pt\text{for some }o\text{ of }D &\\\textbf{1,3,4} & (5)\ \text{"}\phi c\text{" is true in }L^{\prime \prime}\text{ for some arbitrary }c& \hfill \textbf{1,3,4 Definition}\\\textbf{1,3,4} & (6)\ \text{"}(\forall x)\phi x\text{" is true }& \textbf{5 }\forall\textbf{I}\\\textbf{2,3} & (7)\ \text{"}(\forall x)\phi x\text{" is false }&\hfill \textbf{2,3 Definition}\\\textbf{1,2,3,4} & (8)\ \curlywedge& \hfill \textbf{6,7 E}{\sim}\\\textbf{1,3,4} & (9)\ \sim(\operatorname{Ext}(x)\not\in \operatorname{Ext}(\forall))& \hfill \textbf{ 2,8 I}{\sim}\\\textbf{1,3,4} & (10)\ \operatorname{Ext}(x)\in \operatorname{Ext}(\forall)& \hfill \textbf{9, Definition}\end{array}\end{align*}$$

The part of reasoning that is relevant for the present discussion is that from (1)–(6), but let us consider the whole argument. The idea that the extension of the variable x is included in the extension of the universal quantifier (10) follows from the idea that the extension of x is the entire domain D (1) and from the open-endedness assumptions (3) and (4), according to which we can extend our initial language L to $L^{\prime \prime }$ by adding new individual constants and predicates. It should be noted that line (3) made a substantial assumption, namely, that the extension of the new introduced predicate $\phi $ is identical with the extension of x, which in conjunction with premise (1) provides us with the intermediary conclusion that the $\operatorname {Ext}(\phi )=D$ . From this intermediary conclusion and (4), it follows –by a substitution rule of variables with individual constants—in line (5) that “ $\phi c$ ” is true, and, the author adds, “for some arbitrary c”. If this is so, then we can apply the universal introduction rule to infer to the truth of “ $(\forall x)\phi x$ ”. The reader may wonder, however, which is the main reason for which “ $\phi c$ ” is true for arbitrary c and, thus, justifies the application of the $\forall $ I-rule? The individual constant c, indeed, was introduced for an arbitrary object from D, but which is the reason for which “ $\phi c$ ” is true? Is it just the fact that we simply stipulate it to be so? At a closer inspection we see that the reason for which “ $\phi c$ is true for some arbitrary c” is that we have assumed from the very beginning that $\phi $ holds for any object from the domain and c is introduced for an object from D. However, this assumption is equivalent with asserting that $\phi $ expresses a property shared by all objects in the domain (maybe a logical or mathematical property). This assumption, however, is not part of the general inferential use of the first-order quantifiers in logical and mathematical reasoning. Moreover, it is not part of the inferentialist thesis that we should know in advance that the formula whose universal closure is to be inferred has the entire domain as its extension. ¹²

If we do not assume that $\phi $ holds for any object from the domain, then although open-endedness justifies us in introducing the individual constant c, we have no reason to hold that “ $\phi c$ is true for some arbitrary c” and, thus, we cannot apply the $\forall $ I-rule. One way to inferentially justify the model-theoretic assumption that the predicate $\phi $ holds for any object from the domain would be to show that each instance of $\phi $ is provable. However, as we shall also discuss below, we can easily consider a case of reasoning in first-order Peano Arithmetic where $\phi $ is taken to express a mathematical property which holds for each object from the denumerable infinite domain D, but in order to consider $\phi $ an inferable formula, we need to implicitly assume an infinitary rule of inference that legitimates the derivation of an open formula $\phi $ , with at most x free, from its denumerably infinite number of instances:

$$\begin{align*}\{\phi[t/x]: t \text{ is a term of } L\} \vdash \phi. \end{align*}$$

This rule is needed because there are cases, as the one mentioned, when we can prove that a property holds for each object, although we cannot prove that it holds for an arbitrary object. The use of this rule makes unproblematic the derivation of “ $(\forall x)\phi x$ ” from $\phi $ in the next step. Carnap [10] also used a rule of this kind in order to block the non-standard valuation $v^+$ . Once the sentential function $\phi $ is derivable from the infinite conjunctive set of all its instances, i.e., $\{\phi [t/x]: t \text { is a term of } L\}$ , then the rules of Carnap’s [10] formalism (T28-4b) license the derivation of the sentence $(\forall x)\phi x$ from $\phi $ , where x is the only free variable in $\phi $ (T30-2 in [10, p. 146]). Once this rule is present, the non-standard valuation $v^{\omega }$ is also blocked since the set $\{\phi [t/x]: t \text { is a term of }L\}\cup \{\sim (\forall x)\phi x\}$ will be inconsistent in the presence of this rule.

In other words, the standard meaning of the first-order universal quantifier is uniquely determined by the standard natural deduction rules if we assume that the $\operatorname {Ext}(\phi )$ is the entire domain. However, this is a semantic (or model-theoretic) assumption ¹³ and its proof-theoretical counterpart assumption is to accept an infinitary rule of inference that legitimates the inference from an infinite set of instances $\{\phi [t/x]: t \text { is a term of } L\}$ to $\phi $ , since there are cases when $\phi $ demonstrably holds for each object, but we cannot inferentially prove that it holds for an arbitrary object. ¹⁴ Hence, from an inferential perspective, Warren’s argument seems to succeed if the semantic assumptions are inferentially replaced by introducing an infinitary rule of inference in the logical calculus that we use. More generally, since by the Löwenheim–Skolem theorem every first-order theory has an infinite denumerable model, then we need to explicitly assume the use of the infinitary $\omega $ -rule in order to eliminate the non-standard valuations $v^+$ and $v^{\omega }$ from $V(L)$ and, thus, to make L categorical (we will come back to this point in Section 6):

(ω-rule) $$ \begin{align} \frac{\Gamma \vdash \phi t_1, \phi t_2, \dots \text{for all terms }t\text{ of }L} {\Gamma \vdash \forall x \phi x}.\end{align} $$

5 Locally valid open-ended rules for restoring categoricity

Murzi and Topey [29] argued that the local validity of the natural deduction rules for the universal quantifier restores the categoricity of the first-order quantifiers, if these rules are taken to be open-ended. Their approach takes into account Garson’s [18] precisification of the categoricity problem as being relative both to the format of the proof-theoretic system for a logic (axiomatic, natural deduction, and sequent calculi) and to the way in which the validity of the rules of inference is defined (by deductive models, global models, or local models).

Definition 5. V is a local model of a rule R iff R preserves V-satisfaction; where a rule R preserves V-satisfaction iff for each member v of V, v satisfies R. A valuation v satisfies R iff whenever v satisfies the inputs of R, it also satisfies the output of R.

Garson [18, pp. 42–43] argued that the use of the local models makes the introduction rule for the universal quantifier unsound since a valuation may satisfy the premise $\Gamma \vdash \phi t$ without satisfying ipso facto the conclusion $\Gamma \vdash (\forall x)\phi x$ , even if t does not occur in $\Gamma $ . ¹⁵ In addition, if all valuations v from a local model V would simultaneously satisfy both the universal introduction and elimination rules, then we would have a collapse of quantification, i.e., $\phi x\leftrightarrow \forall x\phi x$ . Thus, Garson abandoned the local models for the global ones. ¹⁶ Murzi and Topey [29, p. 3403] consider this abandonment to be made too quickly and argue that the local models could be used, with some emendations of the formalism, even for the quantifiers. They introduce a form of the $\forall $ I-rule that allows open sentences in the premise sequent:

(∀I) $$ \begin{align} \frac{\Gamma\vdash\phi}{\Gamma\vdash\forall x \phi }\text{ where }x\text{ does not appear free in }\Gamma.\end{align} $$

Their strategy for obtaining the categoricity of the first order quantifier has two steps: first they argue for a weakened thesis and then this thesis is generalized for obtaining the result that the local validity of the open-ended natural deduction rules for the universal quantifier is a necessary condition for their categoricity, i.e., all valuations from $V(L)$ are such that $\forall x\phi x$ is true in v iff $\operatorname {Ext}_v(\phi )$ in v is the entire domain. The generalized thesis is inferentially obtained by using the open-endedness of the universal elimination rule, but since I take this step to be unproblematic for the existence of the non-standard valuations for $\forall $ , let us take a look at the proof for the weakened thesis. Likewise, for the same reason, I shall consider only the necessity direction of the proof.

Weakened First Order Thesis. The rules of FOL are locally valid with respect to a class of valuations $V\setminus \{v^{\top }, v^{\vdash }\}$ only if all $v\in V$ are such that, for any $\phi $ , $\forall x\phi $ is true in v iff $\operatorname {Ext}_v(x)\subseteq \operatorname {Ext}_v(\phi )$ . ¹⁷

Proof (Necessity) Suppose the first-order rules are satisfaction-preserving in v, and let $\phi $ be any formula with at most x free. First, suppose every object in the range of x in v is in $\operatorname {Ext}_v(\phi )$ . Then $v \text{satisfies}_\text{s} \vdash \phi $ for any variable assignment s, in which case v satisfies $\vdash \phi $ . So, since $\forall $ I is satisfaction-preserving, v satisfies $\vdash \forall x \phi $ as well—i.e., $\forall x \phi $ is true in v.

For better referring to the individual steps of the reasoning involved in this proof, I shall also reconstruct it as a Lemmon-style natural deduction derivation:

$$\begin{align*}\begin{array}{llr} \textbf{1} & (1)\ \forall\text{I-rule is satisfaction preserving }&\hfill \textbf{Premise (Local Validity)}\\ \textbf{2} & (2)\ \operatorname{Ext}_v(x)\subseteq \operatorname{Ext}_v(\phi) &\hfill \textbf{Premise}\\ \textbf{2} & (3)\ v \text{ satisfies }\vdash\phi &\hfill \textbf{2 Definition}\\ \textbf{1, 2} & (4)\ v \text{ satisfies }\vdash \forall x \phi,\text{ i.e.,}\ \forall x \phi\text{ is true in }v &\hfill \textbf{1, 3 }\forall\textbf{I}\\ \end{array}\end{align*}$$

The step that is philosophically problematic in this reasoning can be located in the inference from (3) to (4), but before coming back to this, let us take a look at the whole reasoning. If the extension of the variable x is included in the extension of $\phi $ , then the open sentence $\phi $ will be satisfied by any variable assignment (associated with the valuation v). From this idea it is inferred that the valuation v satisfies the argument $\vdash \phi $ , since $\phi $ is satisfied under any variable assignment (every object over which x ranges being in the extension of $\phi $ ). In the next step, from (3) to (4), $\forall $ I-rule is meant to preserve this satisfaction. The problem that Murzi and Topey associate with this weakened thesis is that it is consistent with the possibility that the variable x ranges only over a subset of D and, thus, there might be an object in D such that no variable assignment assigns it to a variable. This is why the thesis has to be enforced.

The full first-order thesis, i.e., $\forall x \phi $ is true in v iff $\operatorname {Ext}_v(\phi ) = D$ , is obtained by using the open-endedness of the $\forall $ E-rule. Since the open-endedness of this rule guarantees that we can extend our language by adding new names, the validity of the open-ended $\forall $ E-rule is incompatible with the possibility that the weakened thesis lets open. Consider for instance that there would be an object in D which is not in the range of $\forall $ . By open-endedness we can name this object by introducing an individual constant c in an extension of the initial language. However, if $\forall x\phi $ is true, then $\phi c$ also has to be true, otherwise the $\forall $ E-rule would be unsound. Thus, $\operatorname {Ext}_v(\phi ) = D$ .

The argument for the full first-order thesis is identical with the necessity direction of Warren’s [43, pp. 85–86] proof for the idea that $\operatorname {Ext}(x)=D$ iff $\operatorname {Ext}(x)\in \operatorname {Ext}(\forall )$ and, as I mentioned, I take it to be unproblematic. Basically, the reformulation of the natural deduction rules for the quantifiers in terms of variables has to be ‘suspended’ by Murzi and Topey in order to obtain the full first-order thesis. This is so because the open-ended $\forall $ E-rule is necessary for obtaining the full first-order thesis and its application requires the use of individual constants.

Since the $\forall $ I-rule is responsible for the existence of the non-standard valuations $v^+$ and $v^{\omega }$ , let us come back to its use in the reasoning for the weakened thesis. We should emphasize from the very beginning that the $\forall $ I-rule is meant to be a first-order rule and, thus, it has to be a finitary rule, i.e., if a conclusion $\phi $ is derivable from a set of premises $\Gamma $ , then it has to be derivable from a finite subset $\Gamma ^{\prime }$ of $\Gamma $ . Now, if we take for granted the local validity of the $\forall $ I-rule, then we know that if “ $\Gamma \vdash \phi $ ” is satisfied by a valuation v, then “ $\Gamma \vdash \forall x \phi x$ ” will also be satisfied. In particular, the valuation $v^{\omega }$ which assigns $\top $ to each member of $\{\phi [t/x]: t \text { is a term of } L\}$ , also has to assign $\top $ to $(\forall x)\phi x$ in order to preserve the local validity of the rule. But this means that the set $\{\phi [t/x]: t \text { is a term of } L\}\cup \{\sim (\forall x)\phi x\}$ is inconsistent in Murzi and Topey’s formalization of quantificational logic. If this is so, however, we have to acknowledge the presence of an infinitary rule of inference, which guarantees the inconsistency of this set. In other words, $\forall $ I-rule is implicitly taken to be an infinitary rule.

Alternatively, consider now the reasoning from (1) to (4) in the particular first-order case in which we have an infinite denumerable domain and $\phi $ expresses a mathematical property which is true of each object from the domain. In this case, $\phi $ will be satisfied by the valuation v (due to Premise 2), but $\phi $ is not provable unless we assume an infinitary rule of the following type: $\{\phi [t/x]: t \text { is a term of } L\}\vdash \phi $ . Likewise, if we assume that $\phi $ is provable, then we can assert that $(\forall x)\phi $ is also provable only if the $\forall $ I-rule is taken to be an infinitary rule. To be more clear on this point, by assuming that an arbitrary first-order open formula $\phi $ is generally satisfied by a valuation v is to implicitly assume that v satisfies $\phi $ even in the case in which $\phi $ is a logical consequence of an infinite number of premise, without being a consequence of any finite subset of them. This assumption, however, is inferentially justified if and only if we can prove that $\phi $ holds for each individual object from the domain.

In their proof of the weakened thesis, Murzi and Topey [29, p. 3407] use a restricted form of the $\forall $ I-rule:

$$\begin{align*}\frac{\vdash\phi}{\vdash\!(\forall x)\phi x}.\end{align*}$$

The fact that $\Gamma =\emptyset $ means that if $\phi $ is provable, then its universal closure will also be provable. However, the general inferential use of the first-order universal quantifier is not limited only to its uses in pure first-order logic, but also in the application of first-order logic in the formalization of mathematical theories, such as Peano Arithmetic. Thus, if $(\forall x)\phi x$ is taken to be a Gödelian sentence of Goldbach type, ¹⁸ the sentence will be true, but to derive it from $\phi $ one needs to assume the applicability of an infinitary rule of inference. Hence, the local validity of the $\forall $ I-rule makes this rule generally sound and blocks the non-standard valuations $v^+$ and $v^{\omega }$ if and only if we inferentially take this rule to have infinitary powers. In other words, the infinitary features of the rule are hidden under the local conception of validity.

We may thus conclude that the standard, i.e., finite, formalizations of quantificational logic, with or without individual constants in the formulation of the rules, are non-categorical since the valuations $v^+$ and $v^{\omega }$ defined in Section 3 above will be members of $V(L)$ , where L is a standard formalization of first-order logic, i.e., finite formalization. These valuations are L-consistent, but they provide the universal quantifier with semantical meanings different from the intended one. These valuations are proof-theoretically blocked if and only if the $\forall $ I-rule is taken to be non-compact, i.e., infinitary.

6 The $\omega $ -rule and the categoricity of the first-order universal quantifier

Both Carnap’s non-standard valuation $v^+$ and Garson’s valuation $v^{\omega }$ are made possible by the fact that there is a lack of symmetry between the semantical meaning of the universal quantifier (“for all”) and the expressive power of the inferential rules or axioms that govern the use of the sign “ $\forall $ ” in a standard formalization of first-order logic. It seems natural, thus, to obtain a categorical formalization of the universal quantifier by using an infinitary rule of inference such as the $\omega $ -rule. ¹⁹

Lemma. A valuation v is standard if and only if:

1. (1) $v(\forall x\phi x)=\top $ if and only if for all terms t in $\operatorname {Term} v(\phi [t/x])=\top $ ,

2. (2) $v(\forall x\phi x)= \top $ if and only if for all object d in D, $v(\phi [d/x])=\top $ .

As we already mentioned, condition (2) is equivalent to condition (1) if every object in the domain is named (or at least nameable) in the language under consideration. Thus, assuming nameability, (2) reduces to (1). ²⁰

Theorem. The result of adding the $\omega $ -rule in the standard formalizations of first-order logic, i.e., $L^{\omega }$ , is categorical, i.e., all valuations v from $L^{\omega }(V)$ are standard.

Proof (Sufficiency) Let us assume that $v(\forall x\phi x)$ is true and let us assume, in addition, that every object in the domain is nameable. By the $\forall $ E-rule, every instance of $(\forall x)\phi x$ is true, i.e., $v(\phi [t/x])$ is true for all terms t in Term. As a consequence, every object from the domain will be in the extension of the universal quantifier. (Necessity) Let us assume that $v(\phi [t/x])$ is true for each term t in Term. The, by the $\omega $ -rule, $v(\forall x\phi x)$ will also be true.

Probably the main problem with the achievement of the categoricity of the first-order universal quantifier in this simple, maybe too simple, way is a philosophical one, namely, that the $\omega $ -rule is an infinitary rule and, thus, it cannot be systematically followed in practice. One may say that the $\omega $ -rule is a rule for … angels! As a matter of historical fact, this criticism was initially raised by Church [12] for Carnap’s [10] proposal of a full formalization of first-order logic. The problem of following the omega rule was recently addressed by Warren [44], ²¹ who argued for the possibility of following this rule (at least in the case in which its premises are recursively enumerable). Since my aim in this paper was only to address the categoricity of the universal quantifier in an abstract manner, i.e., to see which formalization of first-order logic is such that all valuations in $V(L)$ are standard, I shall not advance here an argument for the followability of the omega rule. However, since in the ordinary mathematical practice we do find pieces of infinitary reasoning, then the logical inferentialists should embed infinitary rules in their theoretical framework if they aim to provide an account for the entire field of deductive reasoning. For the time being, I simply acknowledge the necessity and usefulness of the $\omega $ -rule for attaining some useful and desirable meta-theoretical properties (such as the deductive completeness of PA and, thus, the determinacy of arithmetical sentences). I join Fraenkel, Bar-Hillel and Levy’s [15, p. 286] stance in considering Church’s criticism of the use of non-effective rules of inference as not suitable for the purposes of communication as being not very convincing, since:

Communication may be impaired by this non-effectiveness but is not destroyed. Understanding a language is not an all-or-none affair. Our quite efficient use of ordinary language shows that a sufficient degree of understanding can be obtained in spite of the fact that “meaningfulness”, relative to ordinary language, is certainly not effective.

Although the meaningfulness of ordinary language is non-effective, in spite of usual inconveniences, we can make good use of it and understand each other most of the time. Likewise, it is quite clear that the $\omega $ -rule provides us with a clear-cut understanding of the universal quantifier, despite of its non-effective character. The notions “ $\phi $ is meaningful” and “ $\phi $ is a logical consequence of $\Gamma $ ” are similar with respect to the fact that they are both non-effective. However, we can understand most of the expressions $\phi $ and we can derive most of the sentences $\phi $ from $\Gamma $ in an effective way. If we want to ideally grasp all the meaningful sentences and formally derive all the logical consequences, then the price that we have to pay is the appeal to non-effective instruments, like the $\omega $ -rule. In addition, the $\omega $ -logic is a sound and complete system of logic ²² and also provides us with the deductive completeness of Peano Arithmetic. ²³ The Löwenheim–Skolem theorem prevents us in also obtaining the categoricity of the first-order theories without additional constraints, but, certainly, we cannot obtain so easily all desired properties at once.

Finally, I want to stress the fact that since we are eager to obtain desirable meta-theoretical properties (such as semantic completeness, categoricity, and deductive completeness), then we should probably not follow Hilbert’s reaction to Gödel’s first incompleteness theorem and try to dress the $\omega $ -rule in finitary clothes –whatever these may be. Consider for instance Hilbert’s version of this rule:

(ω_H-rule) $$\begin{align} \frac{\phi(t) \text{ for each numeral } t}{(\forall x)\phi x}.\end{align} $$

Hilbert took this rule to be a finitary one and understood it in the sense that if we have a finitary meta-mathematical method for establishing $\phi (t)$ for each numeral t, then we can conclude $(\forall x)\phi x$ . ²⁴ However, if we accept that there are no finitary rules not-formalizable in the system of Principia Mathematica, then we have to accept that we cannot prove the premise of $\omega _H$ -rule in an inferentially finitary way. For instance, for reductio, consider that we can establish in a finitary manner the premise of $\omega _H$ -rule. Then, one application of the $\omega _H$ -rule leads us to $(\forall x)\phi x$ . This conclusion, however, will be based on the same finitary grounds on which the premise is based. But then, by successive applications of the $\forall $ E-rule, we can ideally obtain an infinite number of premises, each of them being based on the same finitary grounds. However, in this way the difference between the $\omega _H$ -rule, as a finitary rule, and the standard $\omega $ -rule, which is an infinitary rule, vanishes:

$$\begin{align*}\begin{array}{ll@{\qquad\qquad}r} \mathrm{Finitary\ grounds} & (1)\ \ \phi(t)\text{ for each numeral }t& \hfill \textbf{Assumption}\\\mathrm{Finitary\ grounds} & (2)\ \ (\forall x)\phi x& \hfill \omega_H\textbf{-rule}\\\mathrm{Finitary\ grounds} & (3)\ \ \phi t_1& \hfill \textbf{2, }\forall\textbf{E}\\\mathrm{Finitary\ grounds} & (4)\ \ \phi t_2& \hfill \textbf{2, }\forall\textbf{E}\\.................................&............&\\\mathrm{Finitary\ grounds} & (n)\ \ \phi(t)\text{ for each numeral }t& \hfill \textbf{2, }\forall\textbf{E}\\\mathrm{Finitary\ grounds} & (n+1)\ \ (\forall x)\phi x& \hfill 3 \dots n, \omega\textbf{-rule}\\ \end{array}\end{align*}$$

This is so because we can obtain the premises of the $\omega $ -rule, which are denumerably infinite (3 to n), from the $\omega _H$ -rule. From this fact, Potter [31, p. 248] draws the conclusion that “the scope of what is to count as the finitary part of arithmetic is therefore inherently unformalizable”, in the sense that there is no effective test for deciding whether the schematic sentence $\phi (t)$ has been established by finitary methods. By analogy, we can say that the existence of a finite meta-mathematical justification or proof for $\phi $ is implicitly assumed in the arguments of both Warren and Murzi and Topey discussed above. This meta-mathematical proof is implicitly assumed when Warren stipulates that $\phi $ has as extension the entire domain and it is also assumed when Murzi and Topey consider that if $\phi $ is satisfied by the valuation v, then we can assert that $\phi $ is finitary provable and, thus, $(\forall x)\phi x$ is also finitary provable. As we repeatedly mentioned, when $\phi $ expresses a mathematical property shared by each object in a denumerable infinite domain, Gödel’s reasoning guarantees us that the finitary rules of inference are insufficient.

7 The categoricity of Peano Arithmetic

Although both Warren [43] and Murzi and Topey [29] also use an open-endedness requirement for securing the categoricity of Peano Arithmetic, they follow different paths. Warren uses open-ended first-order induction (and the open-ended $\omega $ -rule) to obtain the categoricity of the first-order Peano Arithmetic, while Murzi and Topey argue that the open-ended natural deduction rules for the second-order quantifiers make them categorical by uniquely determining their standard interpretation and, thus, the categoricity of second-order Peano Arithmetic is inferentially secured. The previous discussion of their arguments will make the analysis of their arguments easier. Warren’s argument, I contend, inferentially fails because it assumes that we can legitimately introduce a predicate which stands exactly for the standard natural numbers, while Murzi and Topey’s argument succeeds only if, in addition to nameability, we assume that the introduction natural deduction rule for the second-order quantifier $(\forall _2)$ is, likewise, an infinitary rule.

7.1 Open-ended first-order induction and the $\omega $ -rule

Warren [43, p. 255] explicitly states his argument for the categoricity of first-order Peano Arithmetic (PA):

P1. Our open-ended arithmetical practice rules out any non-standard interpretation of arithmetic that can, in principle, be communicated to us.

P2. Any non-standard interpretation of arithmetic can, in principle, be communicated to us.

C1. Any non-standard interpretation of arithmetic is inadmissible.

C2. Arithmetic is categorical.

The central point of the argument is that any non-standard interpretation can be communicated to us. Considering a non-standard interpretation $\mathbf {\mathcal {M}}$ of PA, Warren takes P2 to imply the possibility of extending our initial language L to $L^+$ by adding two new predicates, one for the standard portion of $\mathbf {\mathcal {M}}$ ( $\operatorname {ST}^{M}$ ) and the other for the entire domain of $\mathbf {\mathcal {M}}$ (M), and also the possibility of possessing an ability of seeing $\mathbf {\mathcal {M}}$ as non-standard. Now, in $L^+$ the following sentence will be true: $(\exists x)(Mx \& \sim \operatorname {ST}^{M}x)$ , since it asserts the existence of a non-standard number in $\mathbf {\mathcal {M}}$ . However, we are pre-committed to the open-ended induction rule, which applied to the predicate $\operatorname {ST}^M$ tells us that:

$$ \begin{align*}(\operatorname{ST}^M0 \ \&\ (\forall x)(\operatorname{ST}^Mx \rightarrow \operatorname{ST}^Msx)) \rightarrow (\forall x)\operatorname{ST}^Mx.\end{align*} $$

Still, since $\mathbf {\mathcal {M}} \models \operatorname {ST}^M0\ \&\ (\forall x)(\operatorname {ST}^Mx \rightarrow \operatorname {ST}^Msx)$ and, also, $\mathbf {\mathcal {M}} \models \sim (\forall x)\operatorname {ST}^Mx$ , it follows that ${\mathcal {M}}$ does not satisfy the open-ended induction rule, and since we are pre-committed to it, we have to dismiss $\mathbf {\mathcal {M}}$ . ²⁵

Warren [43, pp. 256–257] asserts, with no further intermediate steps, that the communicability assumption prevents the reasoning conducted above to be a petitio principii. The reader may wonder, however, why the reasoning is not begging the question. One should bear in mind that we work in an inferential, i.e., syntactic, framework which forbids us to use semantic assumptions which are not inferentially justified. The open-endedness requirement justifies the introduction of the predicate $\operatorname {ST}^M$ , but do we have any inferential guarantee that this predicates really stands for all and only for the standard natural numbers? The answer seems to be: No! The validity of induction does its work only if we already assume that $\operatorname {ST}^M$ stands for all and only for the standard numbers. Consider for support the following analogy: assume that the non-standard interpretations for negation and disjunction can be communicated to us. This means that we have a way of distinguishing the normal truth-tables (NTTs) from the non-NTTs. But for this we need semantic predicates whose extensions have to be stipulated from the very beginning. Likewise, the extension of the predicate $\operatorname {ST}^M$ is stipulated from the very beginning and it is not the result of reading off its meaning from the rules –as the inferentialist point of view would require.

Someone may say that the dismissal of this argument is too quick and that the non-standard model $\mathbf {\mathcal {M}}$ is inferentially blocked by the open-endedness of the induction rule by itself. For as soon as there is a predicate $\phi $ such that $\phi $ holds of 0 and whenever $\phi $ holds of n then it also holds of $n+1$ , yet $(\forall x)\phi x$ does not hold, then one already knows that we are in a model that is inferentially inadmissible—since it violates the validity of open-ended induction. Another way of formulating this reply ²⁶ is to say that the open-ended induction rule is applied to arbitrary predicates and when there is a predicate $\phi $ such that the induction rule becomes invalid, then we know that the model is inferentially inadmissible. Consequently, there seems to be no previous presupposed semantic grasping of what the standard numbers are.

It should be mentioned, however, that the induction rule –as all the other arithmetical laws– is valid in all the models of PA and, thus, even in the non-standard ones. Hence, the predicate $\phi $ that invalidates the induction rule cannot be an ordinary arithmetical predicate from the extended object language of PA. Sure, we find out at the end of the day that $\phi $ is—magically—precisely the predicate which holds for all and only for the standard numbers. The reader may thus wonder: do we have any inferential justification to introduce in our language a predicate $\phi $ as long as we are inferentially blind in seeing the distinction between standard and non-standard natural numbers? Is the introduction of the predicate $\phi $ in an extension of the initial language inferentially justified? Is $\phi $ a predicate that an inferentialist can intelligibly formulate in his language?

I think that it is quite reasonable to believe that a logical inferentialist would extend his language by adding a predicate that is intelligible for him/her. If $\phi $ is such a predicate, then—roughly expressed—it makes sense for the inferentialist. But if it makes sense, then its meaning is determined by some inferential rules. From an inferentialist perspective, however, the distinction between standard and non-standard is non-transparent, since the standard and the non-standard models are indiscernible for the inferentialist. Thus, in order for the argument from open-ended induction to work, we need to be able to formulate or to express what Warren calls the  $\operatorname {ST}^M$ predicate. However, to formulate it, we already need to presuppose that this predicate is inferentially intelligible. But this is precisely the problem at issue, namely, that from an inferential point of view we cannot differentiate between the standard and the non-standard models of PA. This distinction is inferentially nonexistent. Warren assumes however, in P2, that any non-standard interpretation is communicable to us and, thus, this justifies the introduction of the predicate $\operatorname {ST}^M$ . However, the communicability requirement introduces on the back door the semantic distinction between standard and non-standard. Hence, the argument form open-ended induction to the categoricity of PA works if and only if we are inferentially justified to apply induction to the predicate $\operatorname {ST}^M$ . However, since this predicate is inferentially unintelligible, then the inferentialist cannot use it without presupposing a previous semantic grasp of its meaning. The predicate $\operatorname {ST}^M$ would not occur in the language we use unless the distinction between standard and non-standard natural numbers is already inferentially presupposed.

7.2 Open-ended natural deduction rules for $\forall _2$

Murzi and Topey [29] generalize their reasoning for the first-order quantifiers to second-order logic. Structurally, their argument is identical to the first-order case: the weakened second-order thesis is enforced by open-endedness for obtaining the result that the rules for SOL are locally valid relative to a class of valuations V only if all valuations from V obey the standard interpretation of $\forall _2$ . Consider again the necessity direction for the weakened second order thesis:

$$\begin{align*}\begin{array}{llr} \textbf{1} & (1)\ \forall_2\text{I-rule is satisfaction preserving}&\hfill \textbf{Premise (Local Validity)}\\\textbf{2} & (2) \ \operatorname{Ext}_v(X)\subseteq \operatorname{Ext}_v(\phi)&\hfill \textbf{Premise}\\\textbf{2} & (3) \ v\text{ satisfies }\vdash\!\phi& \hfill \textbf{2 Definition}\\\textbf{1,2} & (4)\ v\text{ satisfies }\vdash\!(\forall_2 X)\phi,\text{ i.e., }(\forall_2 X)\phi& \hfill \textbf{1,3 }\forall_2\textbf{I}\\&\kern15pt \text{ is true in }v&\end{array}\end{align*}$$

The $\forall _2$ I-rule used in this argument has the following form:

$$\begin{align*}\frac{\vdash\!\phi}{\vdash\!(\forall_2 X)\phi}.\end{align*}$$

By generalising Garson’s reasoning from Section 3 above, one can easily see that the set $\{\phi [t/x]: T \text { is a relational term of } L\}\cup \{\sim (\forall _2 X)\phi \}$ is consistent in the deductive system of SOL, since the $\forall _2$ I-rule is supposed to be a finitary rule. This allows us to define a valuation $v_2^{\omega }$ which assigns $\top $ to each member of $\{\phi [t/x]: T \text { is a relational term of } L\}$ , but assigns $\perp $ to $(\forall _2 X)\phi $ . As in the reasoning conducted for the first-order case, this valuation is blocked only if the $\forall _2$ I-rule is taken to be an infinitary one. Sure, having such an infinitary rule is necessary for blocking the valuation $v_2^{\omega }$ , but it is not by itself sufficient for obtaining categoricity since the second order domain of quantification will be uncountable when the domain of individuals is denumerably infinite and, thus, a denumerable omega rule would, by itself, not be sufficient. However, since the categoricity of mathematical theories in SOL is obtained with the cost of losing the semantic completeness of this logic, and I take the semantic completeness with respect to a recursive axiomatization to be a desirable property, I shall not pursue further the categoricity of the second-order quantifiers.

8 Categoricity by inferential conservativity

We have seen thus far that the arguments for the categoricity of the first-order universal quantifier, based on the open-endedness requirement, work if the introduction rule for this quantifier is taken to be an infinitary rule, in particular, the $\omega $ -rule. By using this rule we still work in a first-order framework and, thus, the Löwenheim–Skolem theorem prevents us to obtain the categoricity of the first-order Peano Arithmetic. Since I dismissed Warren’s argument based on the communicability of the non-standard models, the reader may wonder how an inferentialist may still obtain the categoricity of the first-order Peano Arithmetic. Building up on some ideas of Dummett [13, pp. 217–220] and Brandom (4, pp. 66–73), I think that the inferentialist has a powerful instrument at his disposal, namely, the requirement of inferential conservativity. I shall briefly present here how the requirement of inferential conservativity works, while I plan to fully develop and defend the argument in another context.

The requirement that the rules of inference for a logical term should introduce only inferentially conservative extensions is well known from Belnap’s [1] discussion of the tonk operator. Although this discussion is limited to the introduction of logical terms, it could very well be extended to the introduction of non-logical expressions. As Brandom [4, p. 68] emphasizes:

Unless the introduction and elimination rules are inferentially conservative, the introduction of the new vocabulary licences new material inferences, and so alters contents associated with the old vocabulary.

This means that the requirement of conservativity for the introduction of a logical term in a language is a necessary condition for blocking new material inferences licensed by the introduction of new vocabulary. However, this condition is not at the same time a sufficient one. New material inferences are possible if the language of a non-categorical mathematical theory is extended.

The problem with the non-standard models for Peano Arithmetic is that they contain non-standard numbers. This idea may be expressed by saying that the first-order formalizations of Peano Arithmetic have models that do not omit the set: $\{c\neq 0, c\neq 1, c\neq 2,\dots \}$ , i.e., there are non-standard models that realize this set. ²⁷ In other words, they allow us to extend the language by introducing a new constant c which is different from all the other numerical individual constants of the initial language. The introduction of this constant simultaneously means that the following inference $\vdash (c\neq 0 \&\ c\neq 1\ \&\ c\neq 2 \dots )$ is inferentially justified in the extended language. However, the introduction of this constant licences a material inference which destroys the inferential conservativity of the system, i.e., it allows inferences which are not inferentially justified on the basis of the axioms and rules previously accepted in the system. For instance, by existentially quantifying over $\vdash (c\neq 0\ \&\ c\neq 1\ \&\ c\neq 2 \dots )$ , we obtain the material inference $\vdash (\exists x)(x\neq 0\ \&\ x\neq 1\ \&\ x\neq 2 \dots )$ which is a written in the old language. This inference, however, alters the meanings of the expressions from the old vocabulary.

Thus, if the requirement of inferential conservativity is at work, then all the models of the first-order formalizations of Peano Arithmetic will omit the set: $\{c\neq 0, c\neq 1, c\neq 2 \dots \}$ and categoricity will thus be easily obtained. In other words, the requirement of inferential conservativity guarantees us that the only admissible models of first-order Peano Arithmetic are the $\omega $ -models. Sure, the requirement on inferential conservativity is a very powerful one, although very reasonable for logical and mathematical languages, and it has to be justified that imposing it is not something arbitrarily done and, thus, just begging (again) the question.