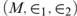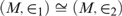Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Väänänen, Jouko
2021.
Tracing Internal Categoricity.
Theoria,
Vol. 87,
Issue. 4,
p.
986.
ROQUE FREIRE, ALFREDO
and
HAMKINS, JOEL DAVID
2021.
BI-INTERPRETATION IN WEAK SET THEORIES.
The Journal of Symbolic Logic,
Vol. 86,
Issue. 2,
p.
609.
Maddy, Penelope
and
Väänänen, Jouko
2024.
Philosophical Uses of Categoricity Arguments.