Article contents
UNIVERSAL CLASSES NEAR 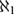 ${\aleph _1}$
${\aleph _1}$
Published online by Cambridge University Press: 21 December 2018
Abstract
Shelah has provided sufficient conditions for an 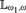 ${\Bbb L}_{\omega _1 ,\omega } $-sentence ψ to have arbitrarily large models and for a Morley-like theorem to hold of ψ. These conditions involve structural and set-theoretic assumptions on all the
${\Bbb L}_{\omega _1 ,\omega } $-sentence ψ to have arbitrarily large models and for a Morley-like theorem to hold of ψ. These conditions involve structural and set-theoretic assumptions on all the 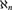 ${\aleph _n}$’s. Using tools of Boney, Shelah, and the second author, we give assumptions on
${\aleph _n}$’s. Using tools of Boney, Shelah, and the second author, we give assumptions on 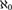 ${\aleph _0}$ and
${\aleph _0}$ and 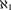 ${\aleph _1}$ which suffice when ψ is restricted to be universal:
${\aleph _1}$ which suffice when ψ is restricted to be universal:
Theorem.Assume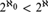 ${2^{{\aleph _0}}} < {2^{{\aleph _1}}}$. Let ψ be a universal
${2^{{\aleph _0}}} < {2^{{\aleph _1}}}$. Let ψ be a universal 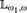 ${\Bbb L}_{\omega _1 ,\omega } $-sentence.
${\Bbb L}_{\omega _1 ,\omega } $-sentence.
(1) If ψ is categorical in
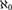 ${\aleph _0}$and
${\aleph _0}$and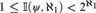 $1 \leqslant {\Bbb L}\left( {\psi ,\aleph _1 } \right) < 2^{\aleph _1 } $, then ψ has arbitrarily large models and categoricity of ψ in some uncountable cardinal implies categoricity of ψ in all uncountable cardinals.
$1 \leqslant {\Bbb L}\left( {\psi ,\aleph _1 } \right) < 2^{\aleph _1 } $, then ψ has arbitrarily large models and categoricity of ψ in some uncountable cardinal implies categoricity of ψ in all uncountable cardinals.(2) If ψ is categorical in
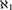 ${\aleph _1}$, then ψ is categorical in all uncountable cardinals.
${\aleph _1}$, then ψ is categorical in all uncountable cardinals.
The theorem generalizes to the framework of 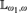 ${\Bbb L}_{\omega _1 ,\omega } $-definable tame abstract elementary classes with primes.
${\Bbb L}_{\omega _1 ,\omega } $-definable tame abstract elementary classes with primes.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
- 7
- Cited by


