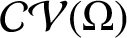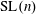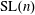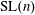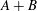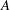23 results
Additive kinematic formulas for convex functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE THIRD HANKEL DETERMINANT FOR INVERSE COEFFICIENTS OF CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 94-100
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
A new inner approach for differential subordinations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 259-272
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN APPLICATION OF SCHUR’S ALGORITHM TO VARIABILITY REGIONS OF CERTAIN ANALYTIC FUNCTIONS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 468-481
- Print publication:
- June 2022
-
- Article
- Export citation
SECOND HANKEL DETERMINANT OF LOGARITHMIC COEFFICIENTS OF CONVEX AND STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 458-467
- Print publication:
- June 2022
-
- Article
- Export citation
ON A CLOSE-TO-CONVEX ANALOGUE OF CERTAIN STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 22 January 2020, pp. 268-281
- Print publication:
- October 2020
-
- Article
- Export citation
INEQUALITIES FOR DRAGOMIR’S MAPPINGS VIA STIELTJES INTEGRALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 240-250
- Print publication:
- October 2020
-
- Article
- Export citation
Non-convex Optimization via Strongly Convex Majorization-minimization
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 726-737
- Print publication:
- December 2020
-
- Article
- Export citation
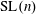 $\text{SL}(n)$ Invariant Valuations on Super-Coercive Convex Functions
$\text{SL}(n)$ Invariant Valuations on Super-Coercive Convex Functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 25 October 2019, pp. 108-130
- Print publication:
- February 2021
-
- Article
- Export citation
TOEPLITZ DETERMINANTS WHOSE ELEMENTS ARE THE COEFFICIENTS OF ANALYTIC AND UNIVALENT FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 253-264
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
Vanishing discount approximations in controlled Markov chains with risk-sensitive average criterion
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 204-230
- Print publication:
- March 2018
-
- Article
- Export citation
FUNCTIONAL VERSIONS OF SOME REFINED AND REVERSED OPERATOR MEAN INEQUALITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 10 August 2017, pp. 496-503
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
SUM THEOREMS FOR MAXIMALLY MONOTONE OPERATORS OF TYPE (FPV)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 08 July 2014, pp. 1-26
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Constructions of Uniformly Convex Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 697-707
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
Predicting the Supremum: Optimality of ‘Stop at Once or Not at All’
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 806-820
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
JENSEN TYPE INEQUALITIES FOR Q-CLASS FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 17 October 2011, pp. 128-142
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
A General ‘Bang-Bang’ Principle for Predicting the Maximum of a Random Walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1072-1083
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Probabilistic Analysis of the Efficacy of Periodic Testing of Employees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1174-1190
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Two New Models for the Two-Person Red-And-Black Game
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 97-108
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Two-person red-and-black games with bet-dependent win probability functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 905-915
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation