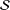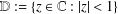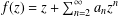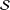Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhang, Hai-Yan
Srivastava, Rekha
and
Tang, Huo
2019.
Third-Order Hankel and Toeplitz Determinants for Starlike Functions Connected with the Sine Function.
Mathematics,
Vol. 7,
Issue. 5,
p.
404.
Srivastava, Hari
Ahmad, Qazi
Khan, Nasir
Khan, Nazar
and
Khan, Bilal
2019.
Hankel and Toeplitz Determinants for a Subclass of q-Starlike Functions Associated with a General Conic Domain.
Mathematics,
Vol. 7,
Issue. 2,
p.
181.
Lecko, Adam
Sim, Young Jae
and
Śmiarowska, Barbara
2020.
The fourth-order Hermitian Toeplitz determinant for convex functions.
Analysis and Mathematical Physics,
Vol. 10,
Issue. 3,
Kowalczyk, Bogumiła
Kwon, Oh Sang
Lecko, Adam
Sim, Young Jae
and
Śmiarowska, Barbara
2020.
The Third-Order Hermitian Toeplitz Determinant for Classes of Functions Convex in One Direction.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 43,
Issue. 4,
p.
3143.
Cudna, K.
Kwon, O. S.
Lecko, A.
Sim, Y. J.
and
Śmiarowska, B.
2020.
The second and third-order Hermitian Toeplitz determinants for starlike and convex functions of order $$\alpha $$.
Boletín de la Sociedad Matemática Mexicana,
Vol. 26,
Issue. 2,
p.
361.
Jastrzȩbski, Piotr
Kowalczyk, Bogumiła
Kwon, Oh Sang
Lecko, Adam
and
Sim, Young Jae
2020.
Hermitian Toeplitz determinants of the second and third-order for classes of close-to-star functions.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 114,
Issue. 4,
Dobosz, Anna
2021.
The Third-Order Hermitian Toeplitz Determinant for Alpha-Convex Functions.
Symmetry,
Vol. 13,
Issue. 7,
p.
1274.
Marut, Musa Josiah
Supramaniam, Shamani
and
Mohd, Maisarah Haji
2021.
Symmetric Toeplitz determinants for starlike and convex functions defined by subordination.
Vol. 2423,
Issue. ,
p.
060003.
Kumar, Virendra
and
Kumar, Sushil
2021.
Bounds on Hermitian-Toeplitz and Hankel determinants for strongly starlike functions.
Boletín de la Sociedad Matemática Mexicana,
Vol. 27,
Issue. 2,
Wang, Dong-rong
Huang, Hua-ying
and
Long, Bo-yong
2021.
Coefficient Problems for Subclasses of Close-to-Star Functions.
Iranian Journal of Science and Technology, Transactions A: Science,
Vol. 45,
Issue. 3,
p.
1071.
Tang, Huo
Khan, Shahid
Hussain, Saqib
and
Khan, Nasir
2021.
Hankel and Toeplitz determinant for a subclass of multivalent $ q $-starlike functions of order $ \alpha $.
AIMS Mathematics,
Vol. 6,
Issue. 6,
p.
5421.
Ahuja, Om P.
Khatter, Kanika
and
Ravichandran, Vaithiyanathan
2021.
Toeplitz Determinants Associated with Ma-Minda Classes of Starlike and Convex Functions.
Iranian Journal of Science and Technology, Transactions A: Science,
Vol. 45,
Issue. 6,
p.
2021.
Lecko, Adam
and
Śmiarowska, Barbara
2021.
Sharp Bounds of the Hermitian Toeplitz Determinants for Some Classes of Close-to-Convex Functions.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 44,
Issue. 5,
p.
3391.
KUMAR, Sushil Kumar
and
ÇETİNKAYA, Asena
2021.
Coefficient Inequalities for certain Starlike and Convex functions.
Hacettepe Journal of Mathematics and Statistics,
Zhang, Hai-Yan
Tang, Huo
and
Ali, Umair
2021.
Fourth Toeplitz Determinants for Starlike Functions Defined by Using the Sine Function.
Journal of Function Spaces,
Vol. 2021,
Issue. ,
p.
1.
Khan, Mohammad Faisal
Goswami, Anjali
and
Khan, Shahid
2022.
Certain New Subclass of Multivalent Q-Starlike Functions Associated with Q-Symmetric Calculus.
Fractal and Fractional,
Vol. 6,
Issue. 7,
p.
367.
Long, Pinhong
Liu, Jinlin
Gangadharan, Murugusundaramoorthy
and
Wang, Wenshuai
2022.
Certain subclass of analytic functions based on $ q $-derivative operator associated with the generalized Pascal snail and its applications.
AIMS Mathematics,
Vol. 7,
Issue. 7,
p.
13423.
Cotîrlă, Luminiţa-Ioana
and
Wanas, Abbas Kareem
2022.
Symmetric Toeplitz Matrices for a New Family of Prestarlike Functions.
Symmetry,
Vol. 14,
Issue. 7,
p.
1413.
Al-shbeil, Isra
Gong, Jianhua
Khan, Shahid
Khan, Nazar
Khan, Ajmal
Khan, Mohammad Faisal
and
Goswami, Anjali
2022.
Hankel and Symmetric Toeplitz Determinants for a New Subclass of q-Starlike Functions.
Fractal and Fractional,
Vol. 6,
Issue. 11,
p.
658.
Lecko, Adam
and
Śmiarowska, Barbara
2022.
Sharp Bounds of the Hermitian Toeplitz Determinants for Certain Close-to-Star Functions.
Bulletin of the Iranian Mathematical Society,
Vol. 48,
Issue. 6,
p.
3077.