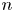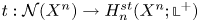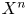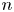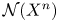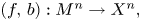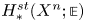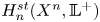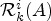9 results
SU(2)-bundles over highly connected 8-manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 February 2025, pp. 1-30
-
- Article
- Export citation
Homotopy classification of 4-manifolds with finite abelian 2-generator fundamental groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. 263-283
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poincaré complex diagonals and the Bass trace conjecture
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1819-1840
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized manifolds, normal invariants, and 𝕃-homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 16 June 2021, pp. 574-589
-
- Article
- Export citation
On Steenrod 𝕃-homology, generalized manifolds, and surgery
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 20 March 2020, pp. 579-607
-
- Article
- Export citation
Poincaré duality and resonance varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 3001-3027
- Print publication:
- December 2020
-
- Article
- Export citation
Homomorphisms of nonzero degree between PDn-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-348
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
Poincare Duality and the Ring of Coinvariants
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 1 / 01 March 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 82-88
- Print publication:
- 01 March 1994
-
- Article
-
- You have access
- Export citation
On Homotopy Domination
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 4 / 01 December 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 448-451
- Print publication:
- 01 December 1984
-
- Article
-
- You have access
- Export citation