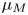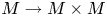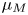Poincaré complex diagonals and the Bass trace conjecture

Abstract

For a finitely dominated Poincaré duality space $M$, we show how the first author's total obstruction $\mu _M$ to the existence of a Poincaré embedding of the diagonal map $M \to M \times M$ in [17] relates to the Reidemeister trace of the identity map of $M$. We then apply this relationship to show that $\mu _M$ vanishes when suitable conditions on the fundamental group of $M$ are satisfied.

1. Introduction

1.1 Poincaré spaces

A distinguishing feature of smooth manifolds is that they carry tangential information: If $M$ is a smooth manifold, then at each point $x\in M$, one may assign a tangent space $T_xM$. The tangent spaces assemble into a vector bundle $\tau _M:\:TM \to M$. If $M$ is compact, then the total space $TM$ is diffeomorphic to a tubular neighbourhood of the diagonal map $M \to M \times M$. The existence of a tubular neighbourhood corresponds to the fact that an $n$-manifold is locally diffeomorphic to $\mathbb {R}^n$ in a suitably parametrized way.

Note that a tubular neighbourhood determines a decomposition

\[ M \times M \cong D(\tau_M) \cup_{S(\tau_M)} C\,, \]

where $D(\tau _M)$ is the tangent disk bundle of $M$, $S(\tau _M)$ is the tangent sphere bundle, and $C$ is the complement of the tubular neighbourhood.

In the 1960s, Browder, Novikov, and Wall developed surgery theory as a tool to classify manifolds up to diffeomorphism in dimensions at least five. A starting point for this theory is that a manifold satisfies Poincaré duality. This led Levitt, Spivak, and Wall to introduce the notion of Poincaré duality space [26, 30]. Such spaces satisfy Poincaré duality globally, however, in contrast with manifolds, duality may fail locally. Nevertheless, Spivak showed that Poincaré spaces can be equipped with stable tangential data: There is a stable spherical fibration, the Spivak tangent fibration, which is unique up to contractible choice, and which can be characterized in a homotopy theoretic way.¹

One is therefore led to the problem as to what a ‘tubular neighbourhood’ of the diagonal of a Poincaré space should be and how it might relate to the Spivak fibration.

If $M$ is a Poincaré duality space formal dimension $n$, then by analogy with the manifold case, one might define a ‘Poincaré tubular neighbourhood’ of the diagonal $\Delta \colon \! M\to M\times M$ to consist of a homotopy theoretic decomposition of the form

\[ M\times M \simeq D(\tau) \cup_{S(\tau)} C, \]

in which $\tau \colon \! S(\tau ) \to M$ is an $(n-1)$-spherical fibration which stabilizes to the Spivak tangent fibration, $D(\tau )$ is the mapping cylinder of $\tau$, and $C$ is some space such that the pair $(C,S(\tau ))$ satisfies Poincaré duality for pairs. The above decomposition amounts to the notion of Poincaré embedding in the special case of the diagonal map [21], [31, §11], [14].

In this paper, we address the following question: When does $M$ possess such a decomposition? Assume in what follows that the formal dimension of $M$ is at least four. In [16], the first author showed that the diagonal admits a Poincaré embedding if $M$ is 1-connected. When $M$ is not $1$-connected then in [17] the first author defined an obstruction $\mu _M$ whose vanishing is both necessary and sufficient for the existence of a Poincaré embedding of the diagonal. However, he was unable to determine when the obstruction vanishes.

Our goal is to relate the obstruction $\mu _M$ to other, more well-known ones. We also apply our main results to prove that $\mu _M$ vanishes in some additional cases.

1.2 The Wall finiteness obstruction

For a group $\pi$, let $K_0(\mathbb {Z}[\pi ])$ be the Grothendieck group of finitely generated projective (left) $\mathbb {Z}[\pi ]$-modules. According to Wall [29], a connected finitely dominated connected space $X$ with fundamental group $\pi$ determines an element

\[ w(X)\in K_0(\mathbb{Z}[\pi]), \]

called the Wall finiteness obstruction. If we assume that $\pi$ is finitely presented, then $X$ has the homotopy type of a finite CW complex if and only if $\tilde w(X)= 0$, where $\tilde w(X) \in \widetilde {K}_0(\mathbb {Z}[\pi ])$ is the image $w(X)$ in the reduced Grothendieck group.

1.3 The Reidemeister characteristic

Let $\bar \pi$ denote the set of conjugacy classes of $\pi$, and let $\mathbb {Z}\langle \bar \pi \rangle$ be the free abelian group with basis $\bar \pi$. The Hattori–Stallings trace [11, 27] is a homomorphism

(1.1)\begin{equation} r\colon\! K_0(\mathbb{Z}[\pi]) \to \mathbb{Z}\langle \bar\pi \rangle \end{equation}

induced by assigning to a finitely generated projective $\mathbb {Z}[\pi ]$-module $P$ the trace of the identity map $P \to P$, where the trace is defined by means of the diagram of homomorphisms

(1.2)\begin{equation} \hom_{\mathbb{Z}[\pi]}(P,P) \overset\cong\leftarrow \hom_{\mathbb{Z}[\pi]}(P,\mathbb{Z}[\pi])\otimes_{\mathbb{Z}[\pi]} P \to \mathbb{Z}[\pi^{\mathrm{ad}}]_\pi = \mathbb{Z}\langle \bar\pi \rangle . \end{equation}

Here, $\hom _{\mathbb {Z}[\pi ]}(P,\mathbb {Z}[\pi ])$ is viewed as a right $\mathbb {Z}[\pi ]$-module and $\pi^\mathrm{ad} = \pi$ considered as a $\pi$-set together with the conjugation action. The second displayed homomorphism in (1.2) is induced by evaluation $f\otimes x\mapsto f(x)$.

For a connected finitely dominated space $X$ with fundamental group $\pi$, the Reidemeister characteristic

\[ r(X) \in \mathbb{Z}\langle \bar\pi \rangle \]

is defined as $r(X) := r(w(X))$.² Let $\widetilde {\mathbb {Z}}\langle \bar \pi \rangle$ denote the cokernel of the inclusion $\mathbb {Z}\langle e \rangle \to \mathbb {Z}\langle \bar \pi \rangle$, where $e \in \pi$ is the trivial element. The reduced Reidemeister characteristic $\tilde r(X)$ is the image of $r(X)$ in $\widetilde {\mathbb {Z}}\langle \bar \pi \rangle$.

Our first main result is:

Theorem A Suppose that $M$ is a connected, finitely dominated Poincaré duality space. If $\tilde r(M) \ne 0$, then the diagonal map $M \to M^{\times 2}$ does not admit a Poincaré embedding.

Remark 1.1 There is currently no known example in which $\tilde r(M) \ne 0$. In fact, the Bass trace conjecture for a group $\pi$ is the statement that the reduced Hattori–Stallings trace

\[ \tilde r\colon\! {\widetilde K}_0(\mathbb{Z}[\pi]) \to \widetilde{\mathbb{Z}}\langle\bar \pi\rangle \]

is trivial [3]. Although the conjecture remains open, it has been verified for a large class of groups, including the residually nilpotent ones. See [5, §3] for more details.

1.4 The diagonal obstruction

Let $d \ge 0$ be an integer. Then the abelian group ${\mathbb {Z}}\langle \bar \pi \rangle$ comes equipped with an involution $\alpha \mapsto \bar \alpha$ induced by the operation $x \mapsto (-1)^{-d}x^{-1}$ for $x\in \pi$. We set

\[ Q_d(\pi) := {\mathbb{Z}}\langle\bar \pi \rangle_{\mathbb{Z}_2}, \]

i.e., the coinvariants of the involution. Similarly, one may define a reduced version of $Q_d(\pi )$ as the cokernel

\[ \tilde Q_d(\pi) := \text{coker}(Q_d(e) \to Q_d(\pi) ), \]

where $e$ denotes the trivial group.

The transfer homomorphism

\[ \tilde{\sigma}\colon\! \tilde Q_d(\pi) \to \widetilde{\mathbb{Z}}\langle\bar \pi \rangle \]

is defined by $\tilde {\sigma }(\alpha ) = \alpha + \bar \alpha$.

Let $M$ be a connected, finitely dominated Poincaré duality space of dimension $d$ and fundamental group $\pi$. Then as alluded to above, in [17] an obstruction

\[ \mu_M \in \tilde Q_d(\pi) \]

was introduced which vanishes if the diagonal map $M\to M\times M$ admits a Poincaré embedding. Conversely, when $d \ge 4$, it was shown that $\mu _M = 0$ implies that a Poincaré embedding of the diagonal exists. The obstruction $\mu _M$ is an invariant of the homotopy type of $M$.

Theorem A is an immediate consequence of our second main result, which relates the Reidemeister characteristic $r(M)$ to the diagonal obstruction $\mu _M$.

Theorem B Let $M$ be a connected, finitely dominated Poincaré duality space. Then

\[ \tilde r(M) = \tilde{\sigma}(\mu_M). \]

In particular, if the diagonal $M \to M^{\times 2}$ admits a Poincaré embedding, then $\tilde r(M) = 0$.

Hypothesis 1.2 $M$ is a connected Poincaré duality space of dimension $d$ such that one of the following conditions hold:

• • $M$ is homotopy finite, or

• • $M$ is finitely dominated and the Bass trace conjecture holds for $\pi = \pi _1(M)$.

Corollary C Assume $M$ satisfies hypothesis 1.2. Then $\tilde \sigma (\mu _M)$ is trivial.

Remark 1.3 As mentioned above, it was known that $\mu _M$ vanishes when $M$ is simply connected or when $M$ has the homotopy type of a closed manifold. The only other case that we were aware of occurs when $M$ is a ‘two-stage patch space’, i.e., a Poincaré space obtained by gluing together two compact manifolds along a homotopy equivalence of their boundaries. If in addition the fundamental group of the boundary is square root closed, then according to Byun [6] there is a diagonal Poincaré embedding, and we infer $\mu _M = 0$ in this instance.

Using corollary C, we obtain several additional cases:

Corollary D Assume that $M$ is a connected, finitely dominated Poincaré space and $d = \dim M \ge 4$ is even. Additionally, assume that $\pi$ is abelian and the 2-primary subgroup of $\pi$ is a finite direct product of cyclic groups of order two. Then the diagonal map $\Delta \colon \! M \to M^{\times 2}$ admits a Poincaré embedding.

Corollary E Assume that $M$ satisfies hypothesis 1.2 with $d \ge 4$. Suppose that every non-trivial element of $\pi$ has odd order. Then the diagonal map $\Delta \colon \! M \to M^{\times 2}$ admits a Poincaré embedding.

The above results justify making the following conjecture.

Conjecture F Assume that $M$ satisfies hypothesis 1.2 with $d \ge 4$. Then the diagonal map $\Delta \colon \! M \to M^{\times 2}$ admits a Poincaré embedding.

Outline. In §2 contains some prerequisites for reading the paper; much of what is contained there is well-known and in the literature. In §3 we introduce the Euler invariant of a Poincaré space equipped with an unstable the Spivak tangent fibration. In §4 we introduce a homotopy-theoretic self-intersection invariant. In §5 is a discussion of the equivariant geometric Hopf invariant as in [7] but in the more general setting of a topological group. The main results are proved in §6.

2. Preliminaries

Here we develop the minimal foundational scaffolding. All of this material has appeared elsewhere and the exposition is not to be regarded as exhaustive.

2.1 Spaces

Let $\mathrm{Top}$ be the Quillen model category of compactly generated weak Hausdorff spaces [12].³ The weak equivalences of $\mathrm{Top}$ are the weak homotopy equivalences, and the fibrations are the Serre fibrations. The cofibrations are defined using the right lifting property with respect to the trivial fibrations. In particular, every object $\mathrm{Top}$ is fibrant. An object is cofibrant whenever it is a retract of a cell complex. We let $\mathrm{Top}_*$ denote the category of based spaces. Then $\mathrm{Top}_*$ inherits a Quillen model structure from $\mathrm{Top}$ by means of the forgetful functor $\mathrm{Top}_\ast \to \mathrm{Top}$.

An object in $\mathrm{Top}$ or $\mathrm{Top}_\ast$ is finite if it is a finite cell complex. It is homotopy finite if it is weakly equivalent to a finite object. A object is $X$ is finitely dominated if it is a retract of a homotopy finite object.

We employ the following notation, most of which is standard. For objects $X,Y\in \mathrm{Top}_\ast$, we let $X\vee Y$ denote the wedge and we let $X\wedge Y$ denote the smash product. The suspension of $X$ is then $S^1 \wedge X$, where $S^1$ is the circle. When we write $X^{[k]}$, we mean the $k$-fold smash product of $X$ with itself. When passing to the stable category of based spaces we sometimes write to indicate a stable map. If $X$ is an unbased space, we write $X_+$ for the based space $X \amalg \ast$ given by taking the disjoint union with a basepoint. For a based space $A$ and an unbased space $B$, our convention will be $A\wedge B_+ := A \wedge (B_+)$ and $B_+ \wedge A := (B_+) \wedge A$.

2.2 Poincaré duality spaces

Recall that an object $M \in \mathrm{Top}$ is a Poincaré duality space of (formal) dimension $d$ if there exists a pair

\[ (\mathscr L,[M]) \]

in which $\mathscr L$ is a rank one local coefficient system (or orientation sheaf) and

\[ [M] \in H_d(M;\mathscr L) \]

is a fundamental class such that for all local coefficient systems $\mathscr B$, the cap product homomorphism

\[{\cap} [M] \colon\! H^\ast(M;\mathscr B) \to H_{d-{\ast}}(M;\mathscr L\otimes\mathscr B) \]

is an isomorphism in all degrees (cf. [19, 30]). The Poincaré spaces considered in this paper are assumed to be connected, finitely dominated and cofibrant. Note that if the pair $(\mathscr L, [M])$ exists, then it is determined up to unique isomorphism by the above property. Also note that closed manifolds are homotopy finite Poincaré duality spaces.

Remark 2.1 Let $p$ be an odd prime. In [30, cor. 5.4.2], a construction is given of a connected finitely dominated Poincaré duality space $K$ of dimension 4 with fundamental group $\pi = \mathbb {Z}/p\mathbb {Z}$. For a suitable choice of $p$, the finiteness obstruction $\tilde w(K) \in \tilde K_0(\mathbb {Z}[\pi ])$ has odd order (for example, $p = 97$ will do, see [24, p. 31]). Then if $j \ge 3$, the product $K\times S^{2j-4}$ is a connected finitely dominated Poincaré duality space of dimension $2j$ having non-trivial finiteness obstruction (this uses [10, thm. 0.1]). For other examples see [20].

More generally, one has the notion of a Poincaré pair $(N,\partial N)$ with fundamental class $[N] \in H_d(N,\partial N; \mathscr L)$. In this case one assumes that the cap product

\[{\cap} [N] \colon\! H^\ast(N;\mathscr B) \to H_{d-{\ast}}(N,\partial N;\mathscr L\otimes\mathscr B) \]

is an isomorphism and in addition the image of $[N]$ with respect to the boundary homomorphism $H_d(N,\partial N; \mathscr L) \to H_{d-1}(\partial N; \mathscr L_{|\partial L})$ equips $\partial N$ with the structure of a Poincaré space of dimension $d-1$.

Given a spherical fibration $\xi \colon \! S(\xi ) \to M$, we write $D(\xi ) \to M$ for the mapping cylinder. The Thom space is the quotient

\[ M^\xi := D(\xi)/S(\xi). \]

Note that the first Stiefel-Whitney class of $\xi$ defines an orientation sheaf $\mathscr L^\xi$. Moreover, by the Thom isomorphism, $H_\ast (M^\xi ) \cong \tilde H_{\ast -k}(M)$, where in the latter, the coefficients are taken with respect to the orientation sheaf.

A Spivak normal fibration for a Poincaré duality space $M$ of dimension $d$ consists of a pair $(\nu,c)$ in which $\nu$ is a $(k-1)$-spherical fibration for some $k$ and

\[ c\colon\! S^{d+k} \to M^\nu \]

is a degree one map in the sense that the image $c_\ast ([S^{d+k}]) \in H_{d+k}(M^\xi ) \cong H_d(M;\mathscr L^\xi )$ is a fundamental class for $M$. The pair $(\nu,c)$ always exists and is unique up to stable fibre homotopy equivalence (see e.g., [15]). The map $c$ is sometimes called the normal invariant.

2.3 Poincaré embeddings of the diagonal

Suppose $M$ is a connected finitely dominated Poincaré duality space of dimension $d$. If $(\mathscr L,[M])$ is a choice of orientation and fundamental class for $M$, then $(\mathscr L^{\times 2},[M]^{\times 2})$ is one for $M\times M$. In particular $M\times M$ is a Poincaré duality space of dimension $2d$.

A diagonal Poincaré embedding of $M$ consists of a map of (finitely dominated) spaces $S(\xi ) \to C$ that fits into a commutative homotopy cocartesian square

in which

• • $\Delta$ is the diagonal map,

• • $\xi$ is a $(d-1)$-spherical fibration,

• • $(C,S(\xi ))$ is a Poincaré pair of dimension $2d$ with orientation sheaf given by the restriction $\mathscr L^{\times 2}_{|C}$ and fundamental class $[C]$ given by taking the image of $[M]^{\times 2}$ under the homomorphism

  \[ H_{2d}(M\times M; \mathscr L^{{\times} 2}) \to H_{2d}(M\times M, M; \mathscr L^{{\times} 2}) \cong H_{2d}(C,S(\xi);\mathscr L^{{\times} 2}_{|C}), \]
  where the displayed isomorphism is given by excision.

It follows that the local system associated to $\xi$ is $\mathscr L^{-1}$. We refer the reader to [19, §5] or [17, §2] for the definition of Poincaré embeddings in full generality.

2.4 $G$-spaces

A topological group object $G$ of $\mathrm{Top}$ is said to be cofibrant if its underlying space is. Let $\mathrm{Top}(G)$ and $\mathrm{Top}_\ast (G)$ denote the category of left $G$-spaces and based left $G$-spaces. We remark here that a right $G$-space can always be converted to a left $G$-space using the involution of $G$ defined by $g \mapsto g^{-1}$.

The categories $\mathrm{Top}(G)$ and $\mathrm{Top}_\ast (G)$ inherit a model structure using the forgetful functor to $\mathrm{Top}$. In both instances, all objects are fibrant. An object of $\mathrm{Top}(G)$ is cofibrant if it is a retract of a free $G$-cell complex, i.e., a space built up from the empty space by free $G$-cell attachments, where a free $G$-cell is defined to be $D^n \times G$ for some $n \ge 0$. Similarly, an object of $\mathrm{Top}_\ast (G)$ is cofibrant if it is built up from a point by based free $G$-cell attachments. In $\mathrm{Top}(G)$ and $\mathrm{Top}_\ast (G)$ one can speak of finite, homotopy finite, and finitely dominated objects.

According to Milnor [23], given a connected based simplicial complex $X$, one may associate a cofibrant topological group $G$ and a universal $G$-principal fibre bundle $\tilde X \to X$. As $\tilde X$ is contractible, it follows that $X$ is identified with $BG$ up to homotopy. On the other hand, any connected space $Y$ is weakly equivalent to a simplicial complex $X$. It follows that $Y$ is weakly equivalent to $BG$.

Remark 2.2 In this case, one can identify the homotopy category of $\mathrm{Top}(G)$ with $\mathrm{Top}/X$, that is spaces over $X \simeq BG$. Concretely, a $G$-space $E$ is sent to $E_{hG} \to \star _{hG} = BG$, whereas to a map $f \colon Z \to X$ we assign the $G$-space $\tilde X \times _X Z$ which models the homotopy fibre of $f$ as a $G$-space.

If $X, Y\in \mathrm{Top}_\ast (G)$ are objects, we write

\[ [X,Y]_G \]

for the set of homotopy classes of based $G$-maps $X\to Y$. Similarly, we write

\[ \{X,Y\}_G \]

for the abelian group of homotopy classes of stable $G$-maps .

2.5 Naive $G$-spectra

We will also be considering the category $\mathrm{Sp}(G)$ of (naive) $G$-spectra formed from objects of $\mathrm{Top}_\ast (G)$. A $G$-spectrum $E$ in this sense consists of based $G$-spaces $E_n$ for $n \ge 0$ together with based $G$-maps $\Sigma E_n \to E_{n+1}$ (structure maps), where $G$ acts trivially on the suspension coordinate of $\Sigma E_n$. A morphism $f\colon \! E\to E'$ of $G$-spectra consists of based $G$-maps of $f_n \colon \! E_n \to E_n'$ for all $n$ which are compatible with the structure maps.

Then $\mathrm{Sp}(G)$ forms a model category in which the fibrant objects are the $\Omega$-spectra and the weak equivalences are the maps which induce isomorphisms on homotopy groups after applying fibrant replacement [25].

Notation 2.3 We indicate a weak equivalence $f\colon \! E\to E'$ with the decoration $\overset\sim\to$. If there is a finite chain of weak equivalences connecting $E$ to $E'$, then by slight notational abuse, we write $E \simeq E'$.

Let $S$ denote the sphere spectrum. Given any $G$-space $X$ its suspension spectrum $\Sigma ^\infty (X_+):= S \wedge X_+$, is naturally a $G$-spectrum. We will sometimes denote it by

\[ S[X]. \]

Remark 2.4 It is sometimes convenient to think of a $G$-spectrum as a collection of based $G$-spaces $E_V$ indexed over finite dimensional inner product spaces $V$, together with $G$-maps $S^W \wedge E_V \to E_{V\oplus W}$.

Given a based $G$-space $X$ and a $G$-spectrum $E$, we may form the spectrum of equivariant maps from $X$ to $E$:

\[ F_G(X,E). \]

The $n$-th space of $F_G(X,E)$ is given by the function space $F_G(X,E_n)$ consisting of based $G$-maps $X\to E_n$. For $F_G(X,E)$ to have a sensible homotopy type, one should assume that $X$ is cofibrant and that $E$ is fibrant. Similarly, one may form

\[ X \wedge_G E, \]

which is the spectrum having $n$-space $X\wedge _G E_n$, i.e., the orbits of $G$ acting diagonally on the smash product $X\wedge E_n$. For this construction to have a sensible homotopy type, we should assume that $X$ and $E$ are cofibrant. We will implicitly apply fibrant/cofibrant replacement to arrange that the above constructions are always homotopy invariant.

As a special case of the above, let $EG$ be a cofibrant free contractible $G$-space. Then the homotopy fixed points and homotopy orbits of $G$ acting on $E$ are given by

\[ E^{hG} := F_G(EG_+,E) \quad \text{and} \quad E_{hG} := E\wedge_G EG_+. \]

2.5.1 Function spectra and smash products

By resorting to one of the standard enriched model categories of spectra [8, 13], we can form internal hom objects

\[ \hom(X,Y) \]

for naive spectra $X$ and $Y$.

Note that $X$ should be cofibrant and $Y$ should be fibrant for the function spectrum to be homotopy invariant. If $X$ and $Y$ are naive $G$-spectra in one of these categories, then $\hom (X,Y)$ is equipped with a $(G\times G)$-action and restricting to the $G$-equivariant functions gives the spectrum

\[ \hom_G(X,Y). \]

When $X = \Sigma ^\infty Z$ is a suspension spectrum of a (cofibrant) $G$-space, then one has an identification

\[ \hom_G(X,Y) \simeq F_G(Z,Y). \]

Similarly, the smash product $X\wedge Y$ has the structure of a $(G\times G)$-spectrum and the orbits under the diagonal action of $G$ defines a spectrum $X\wedge _G Y$. Moreover, $X\wedge _G Y \simeq Z\wedge _G Y$ when $X= \Sigma ^\infty Z$.

2.6 The dualizing spectrum

The main reference for this subsection is [15]. Let $G$ be a cofibrant topological group. Let $G^{\ell r}$ denote $G$ with the left action of $G\times G$ given by $(g,h)\cdot x = gxh^{-1}$.

Remark 2.5 The $(G \times G)$-spectrum $S[G^{\ell r}]$ has the following useful property: given any $G$-spectrum $E$, let $E^\ell$ and $E^r$ denote $E$ as a $G \times G$-spectrum with trivial right/left action, respectively. Then one has a natural isomorphism of $(G \times G)$-spectra

\[ E^\ell \wedge S[G^{\ell r}] \cong E^r \wedge S[G^{\ell r}]. \]

If we write $G_\ell$ in place of $G\times 1$ and $G_r$ in place of $1\times G$, then we immediately infer that

\[ (E^\ell \wedge S[G^{\ell r}])_{hG_\ell} \simeq E \simeq (E^r \wedge S[G^{\ell r}])_{hG_r} \]

as $G$-spectra and compatible with the above identification. Similarly, if $E$ is a $(G \times G)$-spectrum, we obtain a $G$-spectrum $E^{\mathrm{ad}}$ by restricting to the diagonal action. We then obtain natural equivalences

(2.1)\begin{equation} (E \wedge S[G^{\ell r}])_{hG_\ell} \simeq E^{\mathrm{ad}} \simeq (E \wedge S[G^{\ell r}])_{hG_r}. \end{equation}

Example 2.6 Let $G^{\mathrm{ad}}$ denote $G$ equipped with its conjugation action $g\cdot x= gxg^{-1}$. We set

\[ S[G^\mathrm{ad}] := S \wedge (G^\mathrm{ad}_+). \]

Then $S[G^\mathrm {ad}] = S[G^{{\ell r}}]^{\mathrm {ad}}$.

The dualizing spectrum of $G$ is the $G$-spectrum

(2.2)\begin{equation} \mathscr D_G := S[G^{\ell r}]^{hG_\ell} = F_{G_\ell}(EG_+,S[G^{\ell r}]), \end{equation}

in which $G$ acts as $G_r$.

For any $G$-spectrum $E$, one has a norm map

(2.3)\begin{equation} \eta = \eta_E \colon\! \mathscr D_G \wedge_{hG} E \to E^{hG} \end{equation}

which is natural in $E$. The map $\eta$ arises by noting that composition of functions gives rise to a pairing

(2.4)\begin{equation} F_{G_\ell}(EG_+,S[G^{\ell r}]) \wedge \hom_{G_\ell}(S[G^{\ell r}],E) \to F_{G_\ell}(EG_+,E) \end{equation}

which is $G$-invariant, and therefore factors through homotopy orbits. The norm map is then obtained using the evident weak equivalence $E \simeq \hom _{G_\ell }(S[G^{\ell r}],E)$. We recall the following.

Theorem 2.7 (Theorem D in [15])

If $BG$ is finitely dominated, then the norm map

\[ \eta_E \colon\! \mathscr D_G \wedge_{hG} E = (\mathscr D_G \wedge E)_{hG} \to E^{hG} \]

is an equivalence for any $G$-spectrum $E$.

Note that the norm map is adjoint to a map of $G$-spectra

\[ \mathscr D_G \wedge_{hG} E \wedge EG_+ \to E, \]

This map can be obtained from the evaluation map

(2.5)\begin{equation} \epsilon\colon\! \mathscr D_G\wedge EG_+ \to S[G^{\ell r}] \end{equation}

which is $(G\times G)$-equivariant. The map $\epsilon$ is defined so that it is adjoint to the identity map of $\mathscr D_G$, i.e., it is given by the evaluating stable maps $EG_+ \to S[G^{\ell r}]$ at points of $EG_+$.

Example 2.8 In the case $E = S$, with $G$ acting trivially, the norm equivalence is

\[ \eta \colon\! \left( \mathscr D_G \right)_{hG} \xrightarrow{\simeq} S^{hG} = F(BG_+,S). \]

Hence, the unit $BG_+ \to S$ corresponds to a map $S \to ( \mathscr D_G )_{hG}$.

This relates to the classical normal invariant of the Spivak normal fibration as follows: Suppose that $M$ is a (connected, finitely dominated) Poincaré duality space of dimension $d$. Let $\tilde M \to M$ be a universal principal bundle over $M$ with topological structure group $G$. Then $\tilde M$ is a free, contractible $G$-space. We may assume that $G$ is cofibrant. Then $\tilde M$ models $EG$ and $M$ models $BG$. In this case $\mathscr D_G$ is unequivariantly weakly equivalent to a sphere of dimension $-d$, and we write

\[ S^{-\tau} := \mathscr D_G \]

in this instance. Then the stable spherical fibration

\[ S^{-\tau} \times_G \tilde M \to M \]

is the Spivak normal fibration of $M$.⁴ In this context, the Thom spectrum $M^{-\tau }$ is identified with $S^{-\tau }_{hG} = S^{-\tau } \wedge _G (\tilde M_+)$, and the norm equivalence in this notation is just Atiyah duality [1] for Poincaré duality spaces:

\[ M^{-\tau} \simeq F(M_+,S). \]

Summarizing, with respect to $E = S$, the norm equivalence specializes to Atiyah duality and the stable normal invariant $S \to M^{-\tau }$ corresponds to the unit $1\colon \! M_+ \to S$.

In what follows we set

\[ S^\tau := \hom(S^{-\tau},S)\wedge EG_+. \]

Then $G=G_\ell$ acts on $S^\tau$ and

\[ S^{\tau} \times_G \tilde M \to M \]

is the stable Spivak tangent fibration of $M$. In what follows we extend the action of $G = G_\ell$ on $S^\tau$ to $G\times G$ by letting $G_r$ act trivially.

2.7 The umkehr map $\Delta _!$

To the diagonal map $\Delta \colon \! M \to M\times M$ we associate a $(G\times G$)-equivariant umkehr map

(2.6)\begin{equation} \Delta_!\colon\! EG_+{\wedge} EG_+ \to S^\tau[G^{\ell r}], \end{equation}

where $S^\tau [G^{\ell r}] := S^\tau \wedge G^{\ell r}_+$. The umkehr map is defined as the evaluation map

\[ EG_+{\wedge} F_{G_\ell}(EG_+,S^\tau[G^{\ell r}]) \to S^\tau[G^{\ell r}], \]

in conjunction with the observation that the norm map with respect to $E= S^\tau [G^{\ell r}]$ defines an equivalence

\[ EG_+{\simeq} \mathscr D_G \wedge_{hG} S^\tau[G^{\ell r}] \mathrel{\mathop{\rightarrow}^{\eta}_{\sim}} F_{G_\ell}(EG_+,S^\tau[G^{\ell r}]) . \]

Remark 2.9 If $M$ is a closed manifold, then the homotopy orbits of $G\times G$ acting on $\Delta _!$ coincides with the map $M_+\wedge M_+ \to M^\tau$ given Pontryagin-Thom collapse of the embedding $\Delta$.

We can now rephrase the norm equivalence in terms of $\Delta _!$. Given any $G$-spectrum $E$ we obtain a map of $G$-spectra

\[ EG_+{\wedge} E_{hG} \cong (EG_+{\wedge} EG_+{\wedge} E^r)_{G_r} \mathrel{\mathop{\rightarrow}^{\Delta_! \wedge \operatorname{id}_E}} (S^\tau[G^{\ell r}] \wedge E^r)_{G_r} \cong S^\tau \wedge E , \]

The proof of the following is straightforward, but tedious. We leave its verification to the reader.

Lemma 2.10 The map adjoint to $\Delta _! \wedge \operatorname {id}_E$ defines a weak equivalence

\[ E_{hG} \mathrel{\mathop{\rightarrow}^{\sim}}(S^\tau \wedge E)^{hG} \]

that is natural in $E$.

3. The tangential Euler invariant

Assume that $M$ is a finitely dominated Poincaré duality space of dimension $d$. Suppose in addition that an (unstable) $(d-1)$-spherical fibration

\[ \xi\colon\! S(\xi) \to M \]

is specified. We also assume that $\xi$ comes equipped with a choice of stable fibre homotopy equivalence to the Spivak tangent fibration of $M$.

Let $D(\xi ) \to M$ be the mapping cylinder of $\xi$. For any space $Y \to M$, let $\tilde Y := \tilde M \times _M Y$. Then $\tilde Y$ is an unbased $G$-space. Define

\[ S^\xi := \tilde D(\xi)/\tilde S(\xi). \]

Then $S^\xi$ is a based $G$-space which is unequivariantly the homotopy type of a $d$-sphere (note: $S^\xi$ models the fibre of the unreduced fibrewise suspension of $\xi$).

In particular, one has a diagonal map

\[ \Delta_\xi\colon\! S^\xi[G^{\ell r}] \to S^\xi[G^{\ell r}]\wedge S^\xi[G^{\ell r}], \]

which depends on $\xi$. In view of the stable identification $S^\xi \simeq S^\tau$, we resort to the notation

\[ \Delta_\xi\colon\! S^\tau[G^{\ell r}] \to S^\tau[G^{\ell r}]\wedge S^\tau[G^{\ell r}] \]

when $\Delta _\xi$ is considered as a stable map.

Definition 3.1 The Euler invariant $\mathfrak e(\xi )$ is the $(G\times G)$-equivariant composition

\[ EG_+ \wedge EG_+ \overset{\Delta_!}\to S^\tau[G^{\ell r}] \overset{\Delta_\xi}\to S^\tau[G^{\ell r}]\wedge S^\tau[G^{\ell r}] \]

Lemma 3.2 There is a preferred isomorphism of abelian groups

\[ \{EG_+{\wedge} EG_+, S^\tau[G^{\ell r}]\wedge S^\tau[G^{\ell r}]\}_{G\times G} \cong H_0(LM), \]

where $LM := \mathrm{map}(S^1,M)$ is the free loop space of $M$.

Remark 3.3 The group $H_0(LM)$ is canonically isomorphic to $\mathbb {Z}\langle \bar \pi \rangle$.

Proof of lemma 3.2 The norm map applied to the $(G\times G)$-spectrum $S^\tau [G^{\ell r}]\wedge S^\tau [G^{\ell r}]$ defines an equivalence

(3.1)\begin{equation} (S^{-\tau}{\wedge} S^{-\tau}) \wedge_{h G^{{\times} 2}} (S^\tau[G^{\ell r}]\wedge S^\tau[G^{\ell r}]) \simeq (S^\tau[G^{\ell r}]\wedge S^\tau[G^{\ell r}])^{hG^{{\times} 2}}. \end{equation}

As $S\simeq _{G} S^{-\tau } \wedge S^\tau$, the left side of (3.1) coincides up to homotopy with

\[ S[G^{\ell r}] \wedge_{hG^{{\times} 2}} S[G^{\ell r}] \simeq (S[G^{\ell r} \times G^{\ell r}])_{hG^{{\times} 2}}. \]

Consider the map $G^{\ell r} \to G^{\ell r} \times G^{\ell r}$ given by the inclusion of $1\times G^{\ell r}$. It is straightforward to check that the induced map of spectra

\[ S[G^{\ell r}]_{hG} \to S[G^{\ell r}] \wedge_{hG^{{\times} 2}} S[G^{\ell r}] \]

is a weak equivalence. But it is well known that $S[G^{\ell r}]_{hG}$ coincides with $\Sigma ^\infty (LM)_+$ (see e.g., [18, lemma 9.1]). Hence, we have defined a weak equivalence of spectra

\[ (S^\tau[G^{\ell r}]\wedge S^\tau[G^{\ell r}])^{hG^{{\times} 2}} \simeq \Sigma^\infty (LM)_+ . \]

The conclusion of the Lemma follows by taking $\pi _0$.

In view of lemma 3.2, we infer that

\[ \mathfrak e(\xi) \in H_0(LM) = \mathbb{Z}\langle \bar\pi \rangle. \]

Proposition 3.4 For any $\xi$ as above, $\mathfrak e(\xi )$ lies in the summand defined by the conjugacy class of the trivial element of $\pi$.

Remark 3.5 The proposition is equivalent to the assertion that $\mathfrak e(\xi ) \in H_0(LM)$ factors through $H_0(M)$. Alternatively, the image of $\mathfrak e(\xi )$ in $H_0(LM,M)$ is trivial.

Proof. Consider the homomorphism

\[ \phi\colon\!\{S^\tau,S^\tau\wedge S^\tau\}_{G} \to \{EG_+{\wedge} EG_+,S^\tau[G^{\ell r}]\wedge S^\tau[G^{\ell r}]\}_{G\times G} \]

induced by assigning to a stable $G$-map $f\colon \! S^\tau \to S^\tau \wedge S^\tau$ the stable $(G\times G)$-map

\[ EG_+{\wedge} EG_+ \mathrel{\mathop{\rightarrow}^{\Delta_! }} S^\tau \wedge G_+^{\ell r} \mathrel{\mathop{\rightarrow}^{f \wedge \Delta_{G_+^{\ell r}}}} S^\tau\wedge S^\tau \wedge G_+^{{\ell r}} \wedge G_+^{{\ell r}}. \]

Then $\Delta _\xi = \phi (\delta _\xi )$, where $\delta _\xi \colon \! S^\xi \to S^\xi \wedge S^\xi$ is the diagonal map of $S^\xi$. Furthermore, smashing with $S^\tau$ defines an isomorphism

\[ \{S,S^\tau\}_{G} \cong \{S^\tau,S^\tau\wedge S^\tau\}_{G}. \]

On the other hand, the norm map applied to $S^\tau$ defines an equivalence

\[ \Sigma^\infty M_+{\simeq} S_{hG} \simeq \mathscr D_G \wedge_{hG} S^{\tau} \mathrel{\mathop{\rightarrow}^{\eta}_{\sim}} (S^{\tau})^{hG} \]

where in the above $G$ acts trivially on $S$ and recall that $\mathscr D_G \simeq S^{-\tau }$. Taking $\pi _0$, we obtain an isomorphism

\[ \{S,S^\tau\}_{G} \cong \pi^{\text{st}}_0(M) = \mathbb{Z}. \]

With respect the identifications, the homomorphism $\phi$ corresponds to inclusion $\mathbb {Z}\langle e\rangle \to \mathbb {Z}\langle \bar \pi \rangle$.

Remark 3.6 With slightly more effort, it is possible to show that

\[ \mathfrak e(\xi) = e(\xi) \cap [M] \in H_0(M), \]

where $e(\xi ) \in H^d(M, \mathscr L^{-1})$ is the (twisted) Euler class of the spherical fibration $\xi$.

4. Self-intersection

Definition 4.1 Let $M$ be a finitely dominated Poincaré duality space as above. The self-intersection invariant of $M$ is the homology class

\[ I(M) \in H_0(LM) \]

given by the $G$-equivariant stable homotopy class of the composition

\[ (EG_+)^{[2]} \overset\Delta\to (EG_+)^{[2]} \wedge (EG_+)^{[2]} \overset{\Delta_! \wedge \Delta_!}\longrightarrow S^\tau[G^{\ell r}] \wedge S^\tau[G^{\ell r}], \]

where we use the identification of lemma 3.2.

4.1 The Reidemeister characteristic

The Reidemeister characteristic of $M$ is the homology class

\[ r(M) \in H_0(LM) \]

which is given by the stable homotopy class of the composition of maps of the form

The first map in this composition is the stable normal invariant and the second map is defined as follows: recall that the evaluation map

\[ \epsilon\colon\! S^{-\tau} \wedge EG_+ \to S[G^{\ell r}] \]

is $(G\times G)$-equivariant. We take homotopy orbits of $\epsilon$ with respect to the diagonal subgroup $G \subset G\times G$ to obtain the map

\[ M^{-\tau} \simeq S^{-\tau}_{hG} \to S[G^\mathrm{ad}]_{hG} \simeq S\wedge ((LM)_+). \]

(cf. [4, 5]).

Remark 4.2 As $M$ is finitely dominated, there is a homotopy finite space $X$ and a factorization of the identity map

\[ M \overset s \to X \overset r \to M. \]

Setting $f = s\circ r\colon \! X \to X$, it follows that $f^{\circ 2} = f$, so $f$ is idempotent. Moreover, if $\pi = \pi _1(M)$, and $u \colon \! M \to B\pi$ classifies the universal cover, then one has the composition

\[ v \colon\! X \overset r \to M \overset u \to B\pi. \]

Consequently, $v \circ f = v$, i.e., $f$ is a map over $B\pi$. Then the generalized Lefschetz trace $L(f) \in \mathbb {Z}\langle \bar \pi \rangle = H_0(LM)$ is defined (cf.[4, §4], [9]). It is not hard to show that

\[ r(M) = L(f). \]

However, we will not make use of this fact.

We next consider the norm equivalence

\[ \eta\colon\! S[G^\mathrm{ad}]_{hG} \overset\sim\to S^\tau[G^\mathrm{ad}]^{hG} := F_G(EG_+, S^\tau[G^\mathrm{ad}]) \]

for the $G$-spectrum $S^\tau [G^\mathrm {ad}]$. Recall that $S^\tau [G^\mathrm {ad}]$ is $S^\tau [G^{{\ell r}}]$ when considered as a $G$-spectrum.

The following result is essentially an unravelling of the definitions. We omit the proof.

Lemma 4.3 With respect to the above norm equivalence, the Reidemeister characteristic $r(M)$ is represented by the $G$-equivariant stable composite

\[ EG_+ \overset \Delta\to EG_+{\wedge} EG_+ \overset{\Delta_!} \to S^\tau[G^{{\ell r}}]. \]

Let $E$ be any $(G\times G)$-spectrum. smashing $\Delta _!$ with $E$ and taking homotopy fixed points, we obtain a map

\[ \Delta_! ^E \colon\! E^{h(G \times G)} \to (E\wedge S^{\tau}[G^{\ell r}])^{h(G \times G)}. \]

In the above, we have implicitly used the fact that the diagonal map $\Delta _{EG_+ \wedge EG_+} \colon EG_+ \wedge EG_+ \to (EG_+ \wedge EG_+)^{[2]}$ is a $(G\times G)$-equivariant weak equivalence.

If we restrict $(G \times G)$-fixed points to $G$-fixed points along the diagonal inclusion $\Delta \colon G \to G \times G$, we obtain a map

\[ \Delta_E^* \colon\! E^{h(G \times G)} \to (E^{\mathrm{ad}})^{hG}. \]

The following lemma in effect says that the maps $\Delta _! ^E$ and $\Delta _E^*$ coincide under the norm equivalence:

Lemma 4.4 Let $E$ be any cofibrant $(G{ \times } G)$-spectrum. Then the following triangle commutes up to homotopy

in which the vertical arrow is given by

\begin{align*} (E^{\mathrm{ad}})^{hG} & \simeq ((E \wedge S[G^{\ell r}])_{hG_\ell})^{hG} \mathrel{\mathop{\rightarrow}^{\eta^{hG}}_{\sim}} ((E \wedge S^\tau[G^{\ell r}])^{hG_\ell})^{hG}\\ & \quad\cong (E \wedge S^\tau[G^{\ell r}])^{h(G \times G)} , \end{align*}

where $\eta$ is the norm equivalence applied to $E \wedge S^\tau [G^{\ell r}]$.

Proof. Note that the diagram is natural in $E$ and the functor $E\mapsto E^{h(G \times G)}$ is represented by $(EG_+)^{[2]} = EG_+ \wedge EG_+$, where to avoid clutter, we have identified $EG_+$ with $S\wedge EG_+$.

Consequently, by the Yoneda lemma, it suffices to show that the two composites

are homotopic. Using that $EG_+$ is the unit we can simplify the diagram to

where the upper composite is adjoint to $\Delta _!$. Note that the unit $S \to (EG_+ \wedge EG_+)^{h(G \times G)}$ is mapped to the unit in $(EG_+)^{hG}$ under the diagonal map. Thus the lower composite is the unit $S \to (EG_+)^{hG}$ composed with the equivalence

\begin{align*} & (EG_+)^{hG} \simeq ((EG_+{\wedge} S[G^{\ell r}])_{hG_\ell})^{hG} \mathrel{\mathop{\rightarrow}^{\eta^{hG}}_{\sim}} ((EG_+{\wedge} S^\tau[G^{\ell r}])^{hG_\ell})^{hG} \cong \\ & \cong (EG_+{\wedge} S^\tau[G^{\ell r}])^{h(G \times G)} \cong (S^\tau[G^{\ell r}])^{h(G \times G)}. \end{align*}

Observe that the last equivalence is obtained from the norm equivalence

\[ \eta \colon\! EG_+ \mathop{\to}\limits^{{\simeq}} (S^\tau[G^{\ell r}])^{hG_\ell} \]

by passing to $G$-homotopy fixed points. Thus the lower composite is adjoint to the $(G \times G)$-equivariant map

\[ EG_+{\wedge} EG_+ \overset{\operatorname{id}\wedge \eta}\longrightarrow EG_+{\wedge} (S^\tau[G^{\ell r}])^{hG_\ell} \to S^\tau[G^{\ell r}], \]

which was the definition of $\Delta _!$ (here, the second displayed map is given by evaluation).

Proposition 4.5 For any finitely dominated Poincaré duality space $M$, we have $I(M) = r(M)$.

Proof. By definition $I(M)$, is the image under $\Delta _! \wedge -$ of $\Delta _!$ itself, where $E = S^\tau \wedge S[G^{\ell r}]$. Lemma 4.4 provides an identification with $r(M)$ in the form of lemma 4.3 in the previous lemma.

Corollary 4.6 If $M$ is homotopy finite, then $I(M) \in H_0(LM)$ lies in summand defined by the conjugacy class of the trivial element of $\pi$.

Proof. By the proposition it is enough to show that $r(M)$ lies in the trivial conjugacy class.

It will be convenient to invoke Waldhausen's algebraic $K$-theory of spaces functor $X\mapsto A(X)$. Here $A(X)$ is the $K$-theory of the category with cofibrations and weak equivalences given by the retractive spaces over $X$ which are relatively finitely dominated [28].

As $M$ is finitely dominated, $M\times S^0$ is a relatively finitely dominated retractive space over $M$ and therefore determines an element of $\pi _0(A(M)) \cong K_0(\mathbb {Z}[\pi _1(M)])$. With respect to this identification, this element is Wall's finiteness obstruction $w(M)$. The image of $w(M)$ in $H_0(LM)$ under the Bökstedt-Dennis trace map [2] is identified with $r(M)$.

If $M$ is homotopy finite, then $w(M)$ lies in the image of the homomorphism $\pi _0(A(\ast )) \to \pi _0(A(M))$. But the composition $\pi _0(A(\ast )) \to \pi _0(A(M)) \to H_0(LM)$ factors through $H_0(L\ast ) =\mathbb {Z}$.

Corollary 4.7 Assume that $M$ is finitely dominated. Suppose that the Bass trace conjecture holds for the group $\pi$. Then the self-intersection invariant $I(M) \in \mathbb {Z}\langle \bar \pi \rangle$ lies in the summand defined by the conjugacy class of the trivial element of $\pi$.

5. Hopf invariants

The main reference for this section is the book of Crabb and Ranicki [7].

Let $Y$ be a cofibrant based $G$-space. Then $Y^{[2]}= Y\wedge Y$ is a based $(\mathbb {Z}_2 \times G)$-space. We may then form the (not naive) $(\mathbb {Z}_2 \times G)$-spectrum

\[ \Sigma^\infty_{\mathbb{Z}_2} (Y^{[2]}). \]

indexed over the complete $\mathbb {Z}_2$-universe $\mathscr U$ (i.e., a countable direct sum of copies of the regular representation $\mathbb {R}[\mathbb {Z}_2]$).

Concretely, the zeroth space of $\Sigma ^\infty _{\mathbb {Z}_2} (Y^{[2]})$ is given by the colimit

\[ \mathop {{\rm colim}}\limits_{V \in \mathscr U} \Omega^VS^V (Y\wedge Y) = \mathop {{\rm colim}}\limits_{V\in \mathscr U} F(S^V,S^V\wedge Y^{[2]}) \]

where $S^V$ is the one-point compactification of $V$ and $F(S^V,S^V\wedge Y^{[2]})$ denotes the function space of unequivariant based maps $S^V\to S^V \wedge Y^{[2]}$.

According to [22, §V.11], one has a tom Dieck fibre sequence of spectra with $G$-action

(5.1)\begin{equation} \Sigma^\infty D_2(Y) \overset \iota\to (\Sigma^\infty_{\mathbb{Z}_2} (Y^{[2]}))^{\mathbb{Z}_2} \overset\phi \to \Sigma^\infty Y. \end{equation}

in which the middle term of (5.1) is the categorical $\mathbb {Z}_2$-fixed point spectrum and $D_2(Y) = Y^{[2]}_{h\mathbb {Z}_2}$ is the quadratic construction.

The zeroth space of the middle term of (5.1) will be denoted by

\[ Q_{\mathbb{Z}_2} (Y^{[2]})^{\mathbb{Z}_2}. \]

Its points are represented by $\mathbb {Z}_2$-equivariant maps $\alpha \colon \! S^V\to S^V \wedge Y^{[2]}$. The zeroth space of the rightmost term of (5.1) is $QY = \Omega ^\infty \Sigma ^\infty (Y)$; its points are represented by a map $\beta \colon \! S^W\to S^W\wedge Y$ for some finite dimensional inner product space $W$.

The displayed map $\phi$ in (5.1) assigns to such an $\alpha$ the induced map of fixed point spaces

\[ \alpha^{\mathbb{Z}_2}\colon\! S^{V^{\mathbb{Z}_2}} \to S^{V^{\mathbb{Z}_2}} \wedge Y \]

where we have used the fact that $Y$ is the fixed point space of $\mathbb {Z}_2$ acting on $Y^{[2]}$. Consequently, on the level of zeroth spaces, there is a homotopy fibre sequence of based $G$-spaces

(5.2)\begin{equation} QD_2(Y) \overset\iota\to Q_{\mathbb{Z}_2} (Y^{[2]})^{\mathbb{Z}_2}\overset\phi\to QY \end{equation}

which is $G$-equivariantly split.

The splitting of (5.2) may be defined as follows: a point of $QY$ is represented by a map $\beta \colon \! S^W \to S^W\wedge Y$ in which $W$ is a trivial $\mathbb {Z}_2$-representation (i.e., a finite dimensional inner product space). This induces the $\mathbb {Z}_2$-equivariant map

\[ S^W \overset{\beta}\to S^W \wedge Y \overset{1_W\wedge \Delta_Y}\longrightarrow S^W\wedge Y^{[2]} \]

representing a point of $Q_{\mathbb {Z}_2} (Y^{[2]})^{\mathbb {Z}_2}$. This provides a section to the map $\phi$ and defines the splitting.

Let $X \in \mathrm{Top}_\ast (G)$ be a finite object. Then a stable $G$-map , is represented by a $G$-map $f_W\colon \! S^W\wedge X \to S^W\wedge Y$. One may associate to $f_W$ the $(\mathbb {Z}_2\times G)$-equivariant map

\[ \Delta_Y \circ f_W\colon\! S^W\wedge X \overset{f_W}\to S^W\wedge Y \overset{1 \wedge \Delta_Y}\longrightarrow S^W\wedge Y^{[2]}. \]

One may also associate to $f_W$ the $(\mathbb {Z}_2\times G)$-equivariant map

$$ (f_W\wedge f_W)\circ \Delta_X\colon\! S^{W\oplus W} \wedge X \overset{1 \wedge \Delta_X}\longrightarrow S^{W\oplus W}\wedge X^{[2]} \overset{f_W\wedge f_W}\longrightarrow S^{W\oplus W}\wedge Y^{[2]}, $$

where it is understood that $W\oplus W$ is given the transposition action of $\mathbb {Z}_2$, and we have implicitly shuffled the factors of the displayed smash product. It follows that $\Delta _Y \circ f_W$ and $(f_W\wedge f_W)\circ \Delta _X$ represent a pair of $G$-maps

\[ \Delta_Y \circ f, (f\wedge f)\circ \Delta_X \colon\! X \to Q_{\mathbb{Z}_2}(Y^{[2]})^{\mathbb{Z}_2}. \]

Furthermore, it is easily checked that these maps are both coequalized by $\phi$:

Set

\[ \{X,Y\wedge Y\}_{G}^{\mathbb{Z}_2} := [X, Q_{\mathbb{Z}_2}(Y^{[2]})^{\mathbb{Z}_2}]_G, \]

i.e., the abelian group of homotopy classes of $G$-equivariant maps $X\to Q_{\mathbb {Z}_2}(Y^{[2]})^{\mathbb {Z}_2}$. Then $\Delta _Y \circ f$ and $(f\wedge f)\circ \Delta _X$ represent elements of $\{X,Y\wedge Y\}_{G}^{\mathbb {Z}_2}$. Moreover, from (5.2) and the above discussion, one has a canonically split inclusion

\[ \iota\colon\! \{X,D_2Y\}_G \to \{X,Y^{[2]}\}_{G}^{\mathbb{Z}_2} . \]

It follows that on the level of homotopy classes, there is a unique $G$-equivariant stable homotopy class

\[ H(f) \in \{X,D_2(Y)\}_{G} \]

such that

(5.3)\begin{equation} \iota\circ H(f) = (f\wedge f)\circ \Delta_X - \Delta_Y \circ f. \end{equation}

Then $H(f)$ is the ( $G$-equivariant geometric) Hopf invariant of the stable $G$-map .

Remark 5.1 In view of the fact that $\iota$ is a split injection, we will typically write $H(f)$ in place of $\iota \circ H(f)$ in (5.3).

Remark 5.2 Crabb and Ranicki [7, §7] only consider the case when $G$ is a discrete group. However, the adaptation to cofibrant topological groups $G$ goes through unchanged. In addition, we note that there is a $1$-connected Hurewicz homomorphism $G\to \pi$, where $\pi = \pi _0(G)$. Under suitable restrictions on the dimension of $X$ and the connectivity of $Y$ (which are fulfilled in the cases we care about), the evident homomorphism

\[ \{X,D_2(Y)\}_G \to \{X\wedge_G (\pi_+),D_2(Y\wedge_G (\pi_+))\}_\pi \]

which carries $H(f)$ to $H(f\wedge _G (\pi _+))$ is an isomorphism. Consequently, $H(f\wedge _G (\pi _+))$ will contain the same information as $H(f)$. The reason we prefer to work with $G$ instead of $\pi$ is that it makes some of the proofs more transparent.

Definition 5.3 The transfer is the composition

\[ \sigma\colon\! \{X,D_2(Y)\}_{G} \overset\iota\to\{X,Y^{[2]}\}_{G}^{\mathbb{Z}_2} \to \{X,Y^{[2]}\}_{G} \]

in which the second homomorphism is induced by forgetting that a map is $\mathbb {Z}_2$-equivariant.

5.1 The diagonal embedding obstruction $\mu _M$

In [17] the first author defines an obstruction to finding a Poincaré embedding of the diagonal as the reduced Hopf invariant of the $(\pi \times \pi )$-equivariant stable map given by inducing $\Delta _!$ along the homomorphism $G\times G \to \pi \times \pi$. After some minor rewriting, takes the form

where $\bar M \to M$ is the universal cover, $\hat M = \bar M \times _\pi (\pi \times \pi )$ and $\hat M^\tau = S^\tau \wedge _{G} ((\pi \times \pi )_+)$. It is straightforward to check that the Hopf invariants in each case coincide (cf. remark 5.2). Hence,

\[ H(\Delta_!) = H(\Delta_! \wedge_{G\times G}( (\pi \times \pi)_+)). \]

It immediately follows that

\[ \mu_M = H(\Delta_!), \]

where $\mu _M$ is the complete obstruction to finding a Poincaré embedding of the diagonal.

Remark 5.4 In the above, we have implicitly used lemma 3.2, remark 3.3 and the proof of proposition 3.4 to define a preferred isomorphism identify $\mathbb {Z}\langle \bar \pi \rangle$ with

\[ \mathbb{Z}\langle \bar \pi \rangle \cong \{EG_+{\wedge} EG_+, S^\tau[G^{\ell r}] \wedge S^\tau[G^{\ell r}] \}_{G} , \]

as well as a preferred isomorphism

\[ Q_d(\pi) \cong \{EG_+{\wedge} EG_+, D_2(S^\tau[G^{\ell r}])\}_{G} . \]

We refer the reader to [17, §6] for more details (note that the discussion in [17, §6] carries over mutatis mutandis from $\pi$-spectra to $G$-spectra).

6. Proof of the main results

As noted in the introduction theorem A follows immediately from theorem B.

Proof of theorem B From the definition of the Hopf invariant we immediately obtain

\[ \sigma H(\Delta_!) = I(M) - \mathfrak e(M) \in H_0(LM). \]

By proposition 3.4, $\tilde {\mathfrak e}(M) \in H_0(LM,M)$ is trivial, and by proposition 4.5

\[ I(M) = r(M). \]

We thus conclude that

\[ \tilde \sigma \mu_M = \tilde \sigma H(\Delta_!) = \tilde r(M), \]

showing the first assertion. The second part follows immediately from [17, theorem A], which states that $\mu _M = 0$ if there exists a Poincaré embedding of the diagonal.

Proof of corollary C If $M$ is homotopy finite or if the Bass trace conjecture holds for $\pi$, then $\tilde r(M) = 0$. The result now follows from theorem B.

Proof of corollary D In this instance, the Bass trace conjecture holds for $\pi$, so $\tilde \sigma (\mu _M) = \tilde r(M)= 0$. The composition

\[ Q_d(\pi) \overset \sigma\to \mathbb{Z} \langle \bar \pi \rangle \to Q_d(\pi) , \]

is given by multiplication by 2, where $\sigma$ is the transfer, and the second displayed map is the projection onto coinvariants. By theorem B, $\tilde \sigma (\mu _M) = 0$. Consequently, $2\mu _M =0$, so by [17, thm. A], it suffices to show that $Q_d(\pi ) = \mathbb {Z} \oplus \tilde Q_d(\pi )$ has no 2-torsion elements (here we have used the fact that $d$ is even to identify $\tilde Q_d(e) =\mathbb {Z}$).

Let use write $\pi$ as a direct product of $H \times K$ in which $H\subset \pi$ is the $2$-primary subgroup. Denote the involution $x \mapsto x^{-1}$ of $\pi$ by $\iota$. Then $\iota$ preserves the decomposition of $\pi$, so $Q_d(\pi ) \cong Q_d(H) \otimes Q_d(K)$. It then suffices to show that $Q_d(H)$ and $Q_d(K)$ are torsion free abelian groups.

Since $d$ is even and $\iota$ fixes $H$ pointwise, we have $Q_d(H) = \mathbb {Z}\langle H \rangle$, so $Q_d(H)$ is torsion free.

Set $K^* = K \setminus \{e\}$. Then $\iota \colon \! K^*\to K^*$ is fixed point free. Consequently, there is a decomposition

\[ K^\ast{=} K_-{\amalg} K_+ \]

in which $K_\pm \subset K^*$ are subsets, and $\iota \colon \! K_- \to K_+$ is an isomorphism. It follows that $\tilde Q_d(K) \cong \mathbb {Z}\langle K_- \rangle$. We infer that $\tilde Q_d(K)$ is torsion free. Hence, $Q_d(K) = \mathbb {Z} \oplus \tilde Q_d(K)$ is also torsion free.

Proof of corollary E. The argument is similar to the proof of corollary D. The composition

\[ \tilde Q_d(\pi) \overset{\tilde \sigma} \to \widetilde{\mathbb{Z}}\langle \bar \pi \rangle \to \tilde Q_d(\pi) , \]

is multiplication by $2$, where the second displayed map is the projection onto coinvariants. By theorem B, $\tilde \sigma (\mu _M) = 0$. Consequently, $2\mu _M = 0$ and it will suffice to show that $\tilde Q_d(\pi )$ has no 2-torsion. We will see that $\tilde Q_d(\pi )$ is torsion free.

Let $\bar \pi ^* =\bar \pi \setminus \{e\}$. Let $\iota \colon \! \pi ^\ast \to \pi ^\ast$ be the involution given by $\iota (x) = x^{-1}$. We claim that $\iota$ defines a induces a free action of $\mathbb {Z}_2$ on $\bar \pi ^*$. We prove this by contradiction: if not, then there are non-trivial elements $g,x\in \pi$ such that

(6.1)\begin{equation} gxg^{{-}1} = x^{{-}1} \end{equation}

Inverting both sides (6.1), we obtain $gx^{-1}g^{-1} = x$. Substituting the last expression into (6.1), we infer that $g^2x^{-1}g^{-2} = x^{-1}$. Inverting both sides of this last expression, we obtain $g^2xg^{-2} = x$.

It follows that $g^2$ commutes with $x$. Let $2k+1$ be the order of $g$. Then $g = (g^2)^{k+1}$ also commutes with $x$. Consequently, $gxg^{-1} = x$. But by assumption $gxg^{-1} = x^{-1}$, so $x = x^{-1}$. Hence, $x^2 = e$ and we obtain a contradiction.

It follows that $\bar \pi ^* = T_- \amalg T_+$ where $\iota$ restricts to an isomorphism $T_- \to T_+$. Hence,

\[ \tilde Q_d(\pi) \cong \mathbb{Z}\langle T_-\rangle \]

is free abelian with basis $T_-$.