Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T20:16:47.832Z Has data issue: false hasContentIssue false
  • English
  • Français

On Steenrod 𝕃-homology, generalized manifolds, and surgery

Part of: Differential topology Homology and cohomology theories Classical Topics in Algebraic Topology Generalized manifolds Categories and geometry Fiber spaces and bundles

Published online by Cambridge University Press:  20 March 2020

Friedrich Hegenbarth  and
Dušan Repovš
Friedrich Hegenbarth
Affiliation:
Dipartimento di Matematica ‘Federigo Enriques’, Università degli studi di Milano, 20133Milano, Italy ([email protected])
Dušan Repovš
Affiliation:
Faculty of Education and Faculty of Mathematics and Physics, University of Ljubljana & Institute of Mathematics, Physics and Mechanics, 1000Ljubljana, Slovenia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to show the importance of the Steenrod construction of homology theories for the disassembly process in surgery on a generalized n-manifold Xn, in order to produce an element of generalized homology theory, which is basic for calculations. In particular, we show how to construct an element of the nth Steenrod homology group 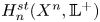$H^{st}_{n} (X^{n}, \mathbb {L}^+)$, where 𝕃+ is the connected covering spectrum of the periodic surgery spectrum 𝕃, avoiding the use of the geometric splitting procedure, the use of which is standard in surgery on topological manifolds.

Keywords

Poincaré duality complexgeneralized manifoldSteenrod 𝕃-homologyperiodic surgery spectrum 𝕃fundamental complex𝕃-homology classQuinn index

MSC classification

Primary: 55N07: Steenrod-Sitnikov homologies 55R20: Spectral sequences and homology of fiber spaces 57P10: Poincaré duality spaces 57R67: Surgery obstructions, Wall groups
Secondary: 18F15: Abstract manifolds and fiber bundles 55M05: Duality 55N20: Generalized (extraordinary) homology and cohomology theories 57P05: Local properties of generalized manifolds 57P99: None of the above, but in this section 57R65: Surgery and handlebodies
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 2 , May 2020 , pp. 579 - 607
Copyright
Copyright © Edinburgh Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to the memory of Professor Andrew Ranicki (1948–2018)

References

1.Bryant, J. L., Ferry, S., Mio, W. and Weinberger, S., Topology of homology manifolds, Ann. Math. 143(2) (1996), 435–467.CrossRefGoogle Scholar
2.Cavicchioli, A., Hegenbarth, F. and Repovš, D., Higher-dimensional generalized manifolds: surgery and constructions, EMS Series of Lectures in Mathematics, Volume 23 (European Mathematical Society, Zurich, 2016).Google Scholar
3.Dugundji, J., Topology (Allyn & Bacon, Boston, 1973).Google Scholar
4.Ferry, S. C., Geometric topology notes, Rutgers University, Piscataway, NJ, 2008. sites.math.rutgers.edu/~sferry/ps/geotop.pdf.Google Scholar
5.Ferry, S. C., Remarks on Steenrod homology, in Novikov conjectures, index theorems, and rigidity (eds. Ferry, S., Ranicki, A. and Rosenberg, J.), pp. 148–166, London Mathematical Society Lecture Note Series 227, Volume 2 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
6.Ferry, S. C., Epsilon-delta surgery over ℤ, Geom. Dedicata 148 (2010), 71–101.CrossRefGoogle Scholar
7.Ferry, S. C. and Pedersen, E. K., Epsilon surgery theory, in Novikov conjecture, index theorem and rigidity (eds. Ferry, S., Ranicki, A. and Rosenberg, J.), pp. 167–226, London Mathematical Society, Lecture Notes Series 227, Volume 2 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
8.Hausmann, J. C. and Vogel, P., Geometry on Poincaré spaces, Mathematical Notes, 41 (Princeton University Press, Princeton, NJ, 1993).Google Scholar
9.Hegenbarth, F. and Repovš, D., Controlled homotopy equivalences on structure sets of manifolds, Proc. Amer. Math. Soc. 142 (2014), 3987–3999.CrossRefGoogle Scholar
10.Hegenbarth, F. and Repovš, D., Controlled surgery and 𝕃-homology, Mediterr. J. Math. 16 (2019), no. 3, Art. 79.CrossRefGoogle Scholar
11.Hu, S. T., Theory of retracts (Wayne State University Press, Detroit, 1965).Google Scholar
12.Jones, L., Patch spaces: a geometric representation for Poincaré spaces, Ann. Math. (2) 97 (1973), 306–343. Corrections, Ann. of Math. (2) 102 (1975), 183–185.CrossRefGoogle Scholar
13.Kahn, D. S., Kaminker, J. and Schochet, C., Generalized homology theories on compact metric spaces, Michigan Math. J. 24(2) (1977), 203–224.Google Scholar
14.Kühl, P., Macko, T. and Mole, A., The total surgery obstruction revisited, Münster J. Math. 6 (2013), 181–269.Google Scholar
15.Levitt, N., Poincaré duality cobordism, Ann. Math. (2) 96 (1972), 211–244.CrossRefGoogle Scholar
16.Marin, A. and Visetti, Y. M., A general proof of Bing's shrinkability criterion, Proc. Amer. Math. Soc. 53(2) (1975), 501–507.Google Scholar
17.Milnor, J., On the Steenrod homology theory, in Novikov conjectures, index theorems, and rigidity (eds. Ferry, S., Ranicki, A. and Rosenberg, J.), pp. 79–96, London Mathematical Society Lecture Note Series 226, Volume 1 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
18.Nicas, A., Induction theorems for groups of homotopy manifold structures, Mem. Amer. Math. Soc. 39(267) (1982).Google Scholar
19.Pedersen, E. K., Quinn, F. and Ranicki, A., Controlled surgery with trivial local fundamental groups, in High-dimensional manifold topology (eds. Farrell, F.T. and Lück, W.), pp. 421–426 (World Scientific Publishing, River Edge, NJ, 2003).CrossRefGoogle Scholar
20.Quinn, F. S., A geometric formulation of surgery, Doctoral Dissertation (Princeton University, Princeton, NJ, 1969).Google Scholar
21.Quinn, F. S., Surgery on Poincaré and normal spaces, Bull. Amer. Math. Soc. 78 (1972), 262–267.CrossRefGoogle Scholar
22.Quinn, F. S., Resolutions of homology manifolds and the topological characterization of manifolds, Invent. Math. 72(2) (1983), 267–284; Corrigendum, Invent. Math. 85 (3) (1986), 653.CrossRefGoogle Scholar
23.Quinn, F. S., An obstruction to the resolution of homology manifolds, Michigan Math. J. 34(2) (1987), 285–291.Google Scholar
24.Ranicki, A. A., The total surgery obstruction, in Proc. Alg. Topol. Conf. Aarhus 1978, pp. 275–316, Lecture Notes Mathematics, Volume 763 (Springer-Verlag, Berlin, 1979).CrossRefGoogle Scholar
25.Ranicki, A. A., Algebraic L-theory and topological manifolds, Cambridge Tracts in Mathematics, Volume 102 (Cambridge University Press, Cambridge, 1992).Google Scholar
26.Yamasaki, M., L-groups of crystallographic groups, Invent. Math. 88(3) (1987), 571–602.CrossRefGoogle Scholar
27.Wall, C. T. C., Poincaré complexes, I., Ann. Math. 86(2) (1967), 213–245.CrossRefGoogle Scholar
28.Wall, C. T. C., Surgery on compact manifolds, 2nd edn, edited and with a foreword by Ranicki, A.A., Mathematical Surveys and Monographs, Volume 69 (American Mathematical Society, Providence, RI, 1999).CrossRefGoogle Scholar
29.Weinberger, S., Homology manifolds, in Handbook of geometric topology, pp. 1085–1102 (North-Holland, Amsterdam, 2002).Google Scholar
30.West, J. E., Mapping Hilbert cube manifolds to ANR's: a solution of a conjecture of Borsuk, Ann. Math. (2) 106 (1977), 1–18.CrossRefGoogle Scholar