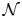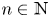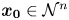13 results
Unique compact representation of magnetic fields using truncated solid harmonic expansions
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convexity of the radial sum of a star body and a ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 289-303
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
The aromatic bicomplex for the description of divergence-free aromatic forms and volume-preserving integrators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 08 August 2023, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the analyticity of WLUD∞ functions of one variable and WLUD∞ functions of several variables in a complete non-Archimedean valued field
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 07 July 2022, pp. 691-704
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality I
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 May 2022, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC ANALYSIS OF SKOLEM’S EXPONENTIAL FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 04 September 2020, pp. 758-782
- Print publication:
- June 2022
-
- Article
- Export citation
An Efficient and Stable Spectral-Element Method for Acoustic Scattering by an Obstacle
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 3 / Issue 3 / August 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 190-208
- Print publication:
- August 2013
-
- Article
- Export citation
Approximate Sampling Formulae for General Finite-Alleles Models of Mutation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 408-428
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
More Eventual Positivity for Analytic Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 5 / 01 October 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1019-1079
- Print publication:
- 01 October 2003
-
- Article
-
- You have access
- Export citation
The mean waiting time of a GI/G/1 queue in light traffic via random thinning
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 256-266
- Print publication:
- March 1995
-
- Article
- Export citation
On a new formula for the transient state probabilities for M/M/1 queues and computational implications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 237-246
- Print publication:
- March 1993
-
- Article
- Export citation
The MacLaurin series for the GI/G/1 queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 176-184
- Print publication:
- March 1992
-
- Article
- Export citation