Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T15:55:45.776Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTIC ANALYSIS OF SKOLEM’S EXPONENTIAL FUNCTIONS

Part of: Real functions Rings and algebras with additional structure Set theory Model theory Approximations and expansions

Published online by Cambridge University Press:  04 September 2020

ALESSANDRO BERARDUCCI  and
MARCELLO MAMINO
ALESSANDRO BERARDUCCI
Affiliation:
DIPARTIMENTO DI MATEMATICA UNIVERSITÀ DI PISA LARGO BRUNO PONTECORVO 5, 56127PISA, ITALYE-mail:[email protected]
MARCELLO MAMINO
Affiliation:
DIPARTIMENTO DI MATEMATICA UNIVERSITÀ DI PISA LARGO BRUNO PONTECORVO 5, 56127PISA, ITALYE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Skolem (1956) studied the germs at infinity of the smallest class of real valued functions on the positive real line containing the constant 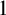$1$ , the identity function 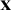${\mathbf {x}}$ , and such that whenever f and g are in the set, 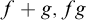$f+g,fg$ and 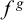$f^g$ are in the set. This set of germs is well ordered and Skolem conjectured that its order type is epsilon-zero. Van den Dries and Levitz (1984) computed the order type of the fragment below 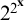$2^{2^{\mathbf {x}}}$ . Here we prove that the set of asymptotic classes within any Archimedean class of Skolem functions has order type 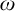$\omega $ . 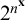As a consequence we obtain, for each positive integer n, an upper bound for the fragment below $2^{n^{\mathbf {x}}}$ . We deduce an epsilon-zero upper bound for the fragment below 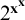$2^{{\mathbf {x}}^{\mathbf {x}}}$ , improving the previous epsilon-omega bound by Levitz (1978). A novel feature of our approach is the use of Conway’s surreal number for asymptotic calculations.

Keywords

Skolem problemsurreal numbersexponentiationordinals

MSC classification

Primary: 03C64: Model theory of ordered structures; o-minimality
Secondary: 03E10: Ordinal and cardinal numbers 16W60: Valuations, completions, formal power series and related constructions 26A12: Rate of growth of functions, orders of infinity, slowly varying functions 41A58: Series expansions (e.g. Taylor, Lidstone series, but not Fourier series)
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 2 , June 2022 , pp. 758 - 782
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altman, H. J., Intermediate arithmetic operations on ordinal numbers . Mathematical Logic Quarterly, vol. 63 (2017), no. 3–4, pp. 228–242.CrossRefGoogle Scholar
Aschenbrenner, M., van den Dries, L., and van der Hoeven, J., Asymptotic Differential Algebra and Model Theory of Transseries , Annals of Mathematics, vol. 195, Princeton University Press, Princeton, NJ, 2017.Google Scholar
Berarducci, A., Kuhlmann, S., Mantova, V., and Matusinski, M., Exponential fields and Conway’s omega-map. Proceedings of the American Mathematical Society , 2018, to appear.Google Scholar
Berarducci, A. and Mantova, V., Surreal numbers, derivations and transseries . Journal of the European Mathematical Society,vol. 20 (2018) no. 2, 339–390.10.4171/JEMS/769CrossRefGoogle Scholar
Berarducci, A. and Mantova, V., Transseries as germs of surreal functions . Transactions of the American Mathematical Society, vol. 371 (2019), no. 5, 3549–3592.CrossRefGoogle Scholar
Carruth, P. W., Arithmetic of ordinals with applications to the theory of ordered Abelian groups . Bulletin of the American Mathematical Society, vol. 48 (2019), no. 4, 262–271.10.1090/S0002-9904-1942-07649-XCrossRefGoogle Scholar
Conway, J. H., On Numbers and Games, London Mathematical Society Monographs, vol. 6, Academic Press, London, UK, 1976.Google Scholar
Dahn, B. I., The limit behaviour of exponential terms . Fundamenta Mathematicae, vol. 124 (1984), no. 2, pp. 169–186.CrossRefGoogle Scholar
van den Dries, L. and Ehrlich, P., Fields of surreal numbers and exponentiation . Fundamenta Mathematicae, vol. 167 (2001), no. 2, 173–188, et Erratum, Fundamenta Mathematicae , vol. 168, no. 2, pp. 295–297.CrossRefGoogle Scholar
van den Dries, L. and Levitz, H., On Skolem’s exponential functions below 22 x . Transactions of the American Mathematical Society, vol. 286 (1984), no. 1, 339–349.CrossRefGoogle Scholar
van den Dries, L., Macintyre, A., and Marker, D., Logarithmic-exponential series . Annals of Pure and Applied Logic, vol. 111 (2001), no. 1-2, pp. 61–113.CrossRefGoogle Scholar
de Jongh, D. H. J. and Parikh, R., Well-partial orderings and hierarchies . Indagationes Mathematicae (Proceedings), vol. 80 (1977), no. 3, pp. 195–207.CrossRefGoogle Scholar
Ehrenfeucht, A., Polynomial functions with exponentiation are well ordered . Algebra Universalis, vol. 3 (1973), no. 1, pp. 261–262.10.1007/BF02945125CrossRefGoogle Scholar
Gonshor, H., An Introduction to the Theory of Surreal Numbers, London Mathematical Society Lecture Notes Series, Cambridge University Press, Cambridge, 1986.CrossRefGoogle Scholar
Gurevič, R., Transcendental numbers and eventual dominance of exponential functions . Bulletin of the London Mathematical Society, vol. 18 (1986), no. 6, pp. 560–570.CrossRefGoogle Scholar
Hahn, H., Über die nichtarchimedischen Grössensysteme . Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften, Mathematisch-Naturwissenschaftliche Classe, vol. 116 (1907), pp. 601–655.Google Scholar
Hardy, G. H., Orders of Infinity, the ‘Infinitärcalcül’ of Paul du Bois-Reymond, Cambridge University Press, Cambridge, 1910.Google Scholar
Kruskal, J. B., Well-quasi-ordering, the tree theorem, and Vazsonyi’s conjecture . Transactions of the American Mathematical Society, vol. 95 (1960), no. 2, p. 210.Google Scholar
Levitz, H., An ordinal bound for the set of polynomial functions with exponentiation . Algebra Universalis, vol. 8 (1978), no. 1, pp. 233–243.CrossRefGoogle Scholar
Lipparini, P., Some transfinite natural sums . Mathematical Logic Quarterly, vol. 64 (2018), no. 6, pp. 514–528.CrossRefGoogle Scholar
Neumann, B. H., On ordered division rings . Transactions of the American Mathematical Society, vol. 66 (1949), no. 1, pp. 202–252.10.1090/S0002-9947-1949-0032593-5CrossRefGoogle Scholar
Richardson, D., Solution of the identity problem for integral exponential functions . Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 15 (1969), no. 20-22, pp. 333–340.CrossRefGoogle Scholar
Schmidt, D., Associative ordinal functions, well partial orderings and a problem of Skolem . Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 24 (1978), no. 19-24, pp. 297–302.CrossRefGoogle Scholar
Sierpiński, W., Cardinal and Ordinal Numbers, Polska Akademia Nauk. Monografie matematyczne tom 34, Państwowe Wydawnictwo Naukowe, Warsaw, 1958, 487 pp.Google Scholar
Skolem, T., An ordered set of arithmetic functions representing the least ε-number . Det Kongelige Norske Videnskabers Selskab Forhandlinger, vol. 29 (1956), pp. 54–59.Google Scholar
Wilkie, A. J., Model completeness results for expansions of the ordered field of real numbers by restricted Pfaffian functions and the exponential function . Journal of the American Mathematical Society, vol. 9 (1996), no. 4, pp. 1051–1094.CrossRefGoogle Scholar