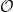 $\mathcal{O}$
$\mathcal{O}$
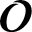 $\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS
$\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS
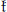 -Type
-Type
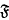 -hyperexcentric modules for Lie algebras
-hyperexcentric modules for Lie algebras