Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T07:15:32.572Z Has data issue: false hasContentIssue false
  • English
  • Français

A new approach to the Koszul property in representation theory using graded subalgebras

Published online by Cambridge University Press:  16 May 2012

Brian J. Parshall  and
Leonard L. Scott
Brian J. Parshall
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA 22903, USA([email protected]; [email protected])
Leonard L. Scott
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA 22903, USA([email protected]; [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a quasi-hereditary algebra 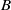, we present conditions which guarantee that the algebra 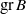obtained by grading 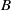by its radical filtration is Koszul and at the same time inherits the quasi-hereditary property and other good Lie-theoretic properties that 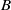might possess. The method involves working with a pair 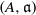consisting of a quasi-hereditary algebra 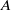and a (positively) graded subalgebra . The algebra 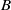arises as a quotient 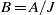of 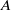by a defining ideal 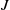of 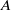. Along the way, we also show that the standard (Weyl) modules for 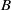have a structure as graded modules for . These results are applied to obtain new information about the finite dimensional algebras (e.g., the 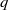-Schur algebras) which arise as quotients of quantum enveloping algebras. Further applications, perhaps the most penetrating, yield results for the finite dimensional algebras associated with semisimple algebraic groups in positive characteristic 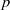. These results require, at least at present, considerable restrictions on the size of .

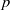Keywords

Koszul algebrasquasi-hereditary algebrasquantum enveloping algebrasalgebraic groupsq-Schur algebrasWeyl modules17B5520G17B50
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 1 , January 2013 , pp. 153 - 197
Copyright
Copyright © Cambridge University Press 2013

References

1.Andersen, H. , Quantum groups at roots of , Comm. Algebra 24 (1996), 3269–3282.CrossRefGoogle Scholar
2.Andersen, H., Jantzen, J. and Soergel, W. , Representations of quantum groups at a th root of unity and of semisimple groups in characteristic , Astérisque 220 (1994).Google Scholar
3.Andersen, H. and Kaneda, M. , Loewy series of modules for the first Frobenius kernel in a reductive algebraic group, Proc. Lond. Math. Soc. 59 (1989), 74–89.CrossRefGoogle Scholar
4.Andersen, H., Polo, P. and Wen, K. , Representations of quantum algebras, Invent. Math. 104 (1991), 571–604.CrossRefGoogle Scholar
5.Andersen, H., Polo, P. and Wen, K. , Injective modules for quantum algebras, Amer. J. Math. 114 (1992), 571–604.CrossRefGoogle Scholar
6.Ariki, S. , Graded -Schur algebras, preprint (arXiv:0903.3454; 2009).Google Scholar
7.Arkhipov, S., Bezrukavnikov, R. and Ginzburg, V. , Quantum groups, the loop Grassmannian, and the Springer resolution, J. Amer. Math. Soc. 17 (2004), 595–678.CrossRefGoogle Scholar
8.Beilinson, A. and Bernstein, J. , Localization of -modules, C. R. Acad. Sci. Paris Ser. I 292 (1981), 15–18.Google Scholar
9.Beilinson, A., Ginzburg, V. and Soergel, W. , Koszul duality patterns in representation theory, J. Amer. Math. Soc. 9 (1996), 473–528.CrossRefGoogle Scholar
10.Brundan, J. and Kleshchev, A. , Blocks of cyclotomic Hecke algebras of Khovanov–Lauda algebras, Invent. Math. 178 (2009), 451–484.CrossRefGoogle Scholar
11.Brundan, J. and Stroppel, C. , Highest weight categories arising from Khovanov’s diagram algebra. II. Koszulity, Transform. Groups 15 (2010), 1–45.CrossRefGoogle Scholar
12.Brylinski, J.-L. and Kashiwara, M. , Kazhdan–Lusztig conjecture and holonomic systems, Invent. Math. 64 (1981), 387–410.CrossRefGoogle Scholar
13.Cline, E., Parshall, B. and Scott, L. , Finite dimensional algebras and highest weight categories, J. Reine Angew. Math. 391 (1988), 85–99.Google Scholar
14.Cline, E., Parshall, B. and Scott, L. , Integral and graded quasi-hereditary algebras, I, J. Algebra 131 (1990), 126–160.CrossRefGoogle Scholar
15.Cline, E., Parshall, B. and Scott, L. , Abstract Kazhdan–Lusztig theories, Tôhoku Math. J. 45 (1993), 511–534.CrossRefGoogle Scholar
16.Cline, E., Parshall, B. and Scott, L. , The homological dual of a highest weight category, Proc. Lond. Math. Soc. 68 (1994), 294–316.CrossRefGoogle Scholar
17.Cline, E., Parshall, B. and Scott, L. , Graded and non-graded Kazhdan–Lusztig theories, in Algebraic groups and Lie groups (ed. Lehrer, G. I. ), pp. 105–125 (Cambridge University Press, 1997).Google Scholar
18.Cline, E., Parshall, B. and Scott, L. , On Ext-transfer for algebraic groups, Transform. Groups 9 (2004), 213–236.CrossRefGoogle Scholar
19.Deng, B., Du, J., Parshall, B. and Wang, J.-P. , Finite dimensional algebras and quantum groups, Math. Surveys and Monographs, Volume 150 (Amer. Math. Soc, 2008).CrossRefGoogle Scholar
20.Dipper, R. and James, G. , The -Schur algebra, Proc. Lond. Math. Soc. 59 (1989), 23–50.CrossRefGoogle Scholar
21.Donkin, S. , On Schur algebras and related algebras, I, J. Algebra 104 (1986), 310–328.CrossRefGoogle Scholar
22.Donkin, S. , The q-Schur algebra, London Math. Soc. Lecture Notes in Mathematics, Volume 253 (London, 1999).Google Scholar
23.Du, J. , A noted on quantized Weyl reciprocity at roots of unity, Algebra Colloq. 2 (1995), 363–372.Google Scholar
24.Du, J. and Scott, L. , Lusztig conjectures, old and new, I, J. Reine Angew. Math. 455 (1994), 141–182.Google Scholar
25.Du, J., Parshall, B. and Scott, L. , Quantum Weyl reciprocity and tilting modules, Comm. Math. Phys. 195 (1998), 321–352.CrossRefGoogle Scholar
26.Fiebig, P. , An upper bound on the exceptional characteristics for Lusztig’s character formula (arXiv:0811.167v2).Google Scholar
27.Green, J., Erdmann, K. and Schocker, M. , Polynomial representations of GLn: with an appendix on schensted correspondence and Littelmann paths, Lecture Notes in Mathematics, Volume 830 (Springer, 2010).Google Scholar
28.Green, E. and Gordon, R. , Graded Artin algebras, J. Algebra 76(1982), 111–137.Google Scholar
29.James, G. , The decomposition matrices of for , Proc. Lond. Math. Soc. 60 (1990), 225–265.CrossRefGoogle Scholar
30.Jantzen, J. C. , Representations of algebraic groups, 2nd edn, Math. Surveys and Monographs, Volume 107 (Amer. Math. Soc, 2003).Google Scholar
31.Jantzen, J. C. , Lectures on quantum groups, Grad. Studies in Math., Volume 6 (Amer. Math. Soc, 1996).Google Scholar
32.Kashiwara, M. and Tanisaki, T. , Kazhdan–Lusztig conjecture for affine Lie algebras with negative level, Duke Math. J. 77 21–62.Google Scholar
33.Kazhdan, D. and Lusztig, G. , Tensor structures arising from affine Lie algebras, I, II, III, IV, J. Amer. Math. Soc. 6 (1993), 905–947; 949–1011, 7 335–381, 383–453.CrossRefGoogle Scholar
34.Lin, Z. , Extensions between simple modules for Frobenius kernels, Math. Z. 207 (1991), 485–499.CrossRefGoogle Scholar
35.Lin, Z. , Comparison of extensions of modules for algebraic groups and quantum groups, in Group representations: cohomology, group actions and topology, Proc. Symp. Pure Math., Volume 63. pp. 355–367. (Amer. Math. Soc, Providence, RI, 1998).CrossRefGoogle Scholar
36.Lusztig, G. , Finite dimensional Hopf algebras arising from quantized universal enveloping algebras, J. Amer. Math. Soc. 3 (1990), 257–296.Google Scholar
37.Lusztig, G. , Quantum groups at a root of 1, Geom. Dedicata 35 (1990), 89–113.CrossRefGoogle Scholar
38.Mazorchuk, V. , Koszul duality for stratified algebras I. Balanced quasi-hereditary algebras, Manuscripta Math. 131 (2010), 1–10.CrossRefGoogle Scholar
39.Mumford, D. , The red book of varieties and schemes, Lecture Notes in Math., Volume 1358 (Springer, 1999).CrossRefGoogle Scholar
40.Parshall, B. and Scott, L. , Derived categories, quasi-hereditary algebras, and algebraic groups, Proc. Ottawa Workshop in Algebra (1987), pp. 1–105.Google Scholar
41.Parshall, B. and Scott, L. , Koszul algebras and the Frobenius endomorphism, Quart. J. Math. 46 (1995), 345–384.CrossRefGoogle Scholar
42.Parshall, B. and Scott, L. , Some -graded representation theory, Quart. J. Math. 60 (2009), 327–351.CrossRefGoogle Scholar
43.Parshall, B. and Scott, L. , A semisimple series for -Weyl and -Specht modules, (arXiv:1109.1489l; 2011).Google Scholar
44.Parshall, B. and Scott, L. , Forced gradings in integral quasi-hereditary algebras, (arXiv:1203.1550).Google Scholar
45.Parshall, B. and Scott, L. , On -filtrations of Weyl modules, preprint in preparation (2012).Google Scholar
46.Priddy, S. , Koszul resolutions, Trans. Amer. Math. Soc. 152 (1970), 39–60.CrossRefGoogle Scholar
47.Riche, S. , Koszul duality and modular representations of semisimple Lie algebras, Duke Math. J. 154 (2010), 31–115.CrossRefGoogle Scholar
48.Tanisaki, T. , Character formulas of Kazhdan–Lusztig type, in Representations of finite dimensional algebras and related topics in Lie theory and geometry, Fields Inst. Commun., Volume 40, pp. 261–276 (Amer. Math. Soc, Providence, RI, 2004).Google Scholar
49.Turner, W. , Rock Blocks, Mem. Amer. Math. Soc. 947 (2009).Google Scholar