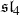Graded extensions of Verma modules

Abstract

In this paper, we investigate extensions between graded Verma modules in the Bernstein–Gelfand–Gelfand category $\mathcal{O}$. In particular, we determine exactly which information about extensions between graded Verma modules is given by the coefficients of the R-polynomials. We also give some upper bounds for the dimensions of graded extensions between Verma modules in terms of Kazhdan–Lusztig combinatorics. We completely determine all extensions between Verma module in the regular block of category $\mathcal{O}$ for $\mathfrak{sl}_4$ and construct various “unexpected” higher extensions between Verma modules.

1. Introduction and description of the results

To determine extensions between Verma modules in Bernstein–Gelfand–Gelfand (BGG) category $\mathcal{O}$ associated to a triangular decomposition of a semi-simple finite dimensional complex Lie algebra $\mathfrak{g}$ is a famous open problem. It was studied in, for example, [ 1, 7, 9–11, 13, 15, 21 ]. The paper [ 15 ] suggested a connection between this problem and a combinatorial gadget, associated to the Weyl group of $\mathfrak{g}$ , called the R-polynomials. Although not explicitly stated in [ 15 ], the expectation that the dimensions of the extension groups between Verma modules should be given by the coefficients of R-polynomials became known as the Gabber–Joseph conjecture. Unfortunately, in [ 7 ] it was shown that this expectation is, in general, wrong. At the present stage, there is not even a conjectural answer to this problem. Some explicit results describing the extension groups between Verma modules in special cases can be found in [ 1, 9, 10, 13, 21 ]. The main result of [ 11 ] determines the Euler characteristic (i.e., the alternating sum) for dimensions of such extensions.

In two recent papers [ 19, 20 ], written jointly with Rafael Mrden, we studied the dimensions of the first extension from a simple module to a Verma module. In the case of the special linear Lie algebra, we gave an explicit formula for this dimension, see [ 19 ]. Outside type A the situation is more complicated. However, an explicit formula can be given in many special cases, see [ 20 ]. These results motivated us to take a new closer look at the classical problem of extensions between Verma modules.

Our first main result, Theorem 2, explicitly determines the role that R-polynomials play in the theory of extensions between Verma modules. Category $\mathcal{O}$ admits a natural $\mathbb{Z}$ -graded lift. Delorme’s formula mentioned above turns out to have a natural graded analogue which asserts that the coefficients of R-polynomials determine the Euler characteristic for dimensions of certain graded extensions between Verma modules. This result can be found in Section 3, see also Subsection 4·3.

In Section 4 we prove a number of general results about extension between graded Verma modules. Combining this additional grading with the homological grading gives a two-dimensional coordinate system (in $\mathbb{Z}^2$ ) in which the potential region for non-zero graded extensions between two fixed Verma modules has the form of a triangle, see Figure 1. If the distance between the indexes of Verma modules is small, then this triangle degenerates to its included side and all extensions are indeed described by the coefficients of the R-polynomials, see Corollary 12. In fact, even in the general case, there are specific situations where graded extensions between Verma modules are given by the coefficients of the R-polynomials, see Corollary 11. In Subsection 4·2 we give several general bounds for the dimension of a fixed extension between graded Verma modules in terms of the Kazhdan–Lusztig combinatorics.

Figure 1. The homomorphisms from $\Delta_x$ to $\mathcal{T}_\bullet(\Delta_y)$ , and thus the extensions from $\Delta_x$ to $\Delta_y$ , are in the dark grey region; the composition factors in $\mathcal{T}_\bullet(\Delta_y)$ are in the light grey region.

Section 5 discusses a few observations about extensions between Verma modules related to the combinatorics of Bruhat order on the Weyl group. In particular, in Proposition 19 we show that graded extension between Verma modules are given by the coefficients of R-polynomials provided that the indexes of the involved Verma modules are both boolean or are both coboolean.

In Section 6 we present a number of concrete results in special cases. In particular, in Theorem 20 we show that in the Weyl type $A_3$ (i.e., for the Lie algebra $\mathfrak{sl}_4$ ) all extensions between Verma modules are given by the coefficients of the R-polynomials despite the nontrivial Kazhdan–Lusztig combinatorics.

Recall the triangle region of potential extensions between Verma modules mentioned above. It has one side included in the region and two sides that are not included. We call the extensions corresponding to the included side “expected” and the extensions corresponding to the interior of the triangle “additional”. If all extensions between two Verma modules are expected, then they are given by the coefficients of the R-polynomials. In Subsection 6·4, we use the results from [ 19 ] to construct families of explicit non-zero additional first extensions between Verma modules in type A. In Subsection 6·5, we use the results from Subsection 6·4 to construct families of explicit non-zero additional second extensions between Verma modules in type A.

The last section of the paper, Section 7, discusses the parabolic and singular cases and the corresponding results similar to the ones that we obtain in the regular case. In particular, Theorem 31 gives a necessary condition for the graded extension algebra of Verma modules to be Koszul.

2. Preliminaries on category $\mathcal{O}$

2·1. Category $\mathcal{O}$

Let $\mathfrak{g}$ be a semi-simple finite dimensional complex Lie algebra with a fixed triangular decomposition $\mathfrak{g}=\mathfrak{n}_-\oplus \mathfrak{h}\oplus \mathfrak{n}_+$ (see [ 16, 25 ] for details). Associated to this datum, we have the Bernstein–Gelfand–Gelfand category $\mathcal{O}$ . See [ 4, 16 ].

Simple modules in $\mathcal{O}$ are exactly the simple highest weight modules $L(\lambda)$ , where $\lambda\in \mathfrak{h}^*$ . For each such $\lambda$ , we also have the corresponding:

1. (1) Verma module $\Delta(\lambda)$ ;

2. (2) dual Verma module $\nabla(\lambda)$ ;

3. (3) indecomposable projective module $P(\lambda)$ ;

4. (4) indecomposable injective module $I(\lambda)$ ;

5. (5) indecomposable tilting module $T(\lambda)$ .

The category $\mathcal O$ is a highest weight category with respect to the dominant order on $\mathfrak{h}^*$ , where $\Delta(\lambda)$ are the standard modules and $\nabla(\lambda)$ are the costandard modules.

Consider the principal block $\mathcal{O}_0$ of $\mathcal{O}$ , which is defined as the indecomposable direct summand containing the trivial $\mathfrak{g}$ -module L(0). Simple modules in $\mathcal{O}_0$ are indexed by the elements of the Weyl group W of $\mathfrak{g}$ . For $w\in W$ , we have the corresponding simple module $L_w\;:\!=\;L(w\cdot 0)$ , where $w\cdot 0$ denotes the usual dot-action of the Weyl group. We similarly denote by $\Delta_w$ , $\nabla_w$ , $P_w$ , $I_w$ and $T_w$ the other structural modules corresponding to the weight $w\in W$ . Then $\mathcal O_0$ is highest weight with respect to the opposite of the Bruhat order on W.

We use Ext and Hom to denote extensions and homomorphisms in $\mathcal{O}$ , respectively. The simple preserving duality on $\mathcal{O}$ is denoted by $\star$ .

2·2. Graded category $\mathcal{O}$

The category $\mathcal{O}_0$ admits a $\mathbb{Z}$ -graded lift $\mathcal{O}_0^{\mathbb{Z}}$ , see [ 28 ]. All structural modules in $\mathcal{O}_0$ admit graded lifts (unique up to isomorphism and shift of grading). We use the following notation for the standard graded lifts of indecomposable structural modules:

1. (1) by ${L}_w$ the graded lift concentrated in degree 0;

2. (2) by ${\Delta}_w$ the graded lift with the top in degree 0;

3. (3) by ${\nabla}_w$ the graded lift with the socle in degree 0;

4. (4) by ${P}_w$ the graded lift with the top in degree 0;

5. (5) by ${I}_w$ the graded lift with the socle in degree 0;

6. (6) by ${T}_w$ the graded lift having the unique $L_w$ subquotient in degree 0.

We denote by $\langle k\rangle$ the functor which shifts the grading, with the convention that $\langle 1\rangle$ maps degree 0 to degree $-1$ . We use ext and hom to denote extensions and homomorphisms in $\mathcal{O}_0^{\mathbb{Z}}$ , respectively. The graded version of $\star$ is also denoted by $\star$ .

2·3. Bruhat order and the zeroth extensions

We recall in this subsection the graded homomorphisms between Verma modules, which is well known (see, for example, [ 12 , chapter 7]). Let $\leq$ be the Bruhat order on W. Then we have

\begin{equation*}\dim\hom(\Delta_x\langle a\rangle,\Delta_y\langle b\rangle ) = \begin{cases}1 &\text{if $x\geq y$ and $b-a = \ell(x)-\ell(y)$}\\0 &\text{otherwise}.\end{cases}\end{equation*}

Moreover, any nonzero homomorphism between Verma modules is injective. Also, the nonzero homomorphisms $L_{w_0}=\Delta_{w_0}\to \Delta_y\langle {\ell(w_0) - \ell(y)} \rangle$ , and their shifts, give the socle of the Verma modules.

2·4. Combinatorics of category $\mathcal{O}_0^{\mathbb{Z}}$

Let $\textbf{H}$ denote the Hecke algebra of W over $\mathbb{Z}[v,v^{-1}]$ in the normalisation of [ 30 ]. It has the standard basis $\{H_w\,:\,w\in W\}$ and the Kazhdan–Lusztig (KL) basis $\{\underline{H}_w\,:\,w\in W\}$ . The KL polynomials $\{p_{x,y}\,:\,x,y\in W\}$ are the entries of the transformation matrix between these two bases, that is

$$ \underline{H}_y=\sum_{x\in W}p_{x,y}H_x, \text{ for all } y\in W.$$

By construction, we have $p_{x,y}\in \mathbb Z[v]$ and $p_{x,y}=0$ for $x\not\leq y$ . When $p_{x,y}\neq 0$ , we have $\deg p_{x,y}=\ell(y)-\ell(x)$ . For $x,y\in W$ and $k\in\mathbb{Z}$ , we denote by $p_{x,y}^{(k)}$ the coefficient at $v^k$ in $p_{x,y}$ .

Taking the Grothendieck group gives rise to an isomorphism of $\mathbb{Z}[v,v^{-1}]$ -modules as follows:

(1) \begin{equation}\textrm{Gr}(\mathcal{O}_0^{\mathbb{Z}}) \cong \textbf{H},\qquad[{\Delta}_w]\mapsto H_w, \text{ for } w\in W.\end{equation}

Here the $\mathbb{Z}[v,v^{-1}]$ -module structure on $\textrm{Gr}(\mathcal{O}_0^{\mathbb{Z}})$ is given by letting the element v act as $\langle -1\rangle$ . By the Kazhdan–Lusztig theorem, see [ 17, 28 ], this isomorphism maps ${P}_w$ to $\underline{H}_w$ , for $w\in W$ . In particular, we have $p_{x,y}\in \mathbb Z_{\geq 0}[v]$ , where its coefficients are the multiplicities of the (graded) filtration of $P_y$ by $\Delta_x$ (see Subsections 2·1, 2·2).

2·5. Endofunctors of $\mathcal{O}_0$

The category $\mathcal{O}_0$ is equipped with the action of various families of functors, see [ 2, 5, 9, 16, 18, 24 ] and references therein. For $w\in W$ , we denote by:

1. (1) $\theta_w$ the indecomposable projective endofunctor of $\mathcal{O}_0$ sending $P_e$ to $P_w$ , see [ 5 ];

2. (2) $\textrm{C}_w$ the corresponding shuffling functor, see [ 9, 24 ];

3. (3) $\top_w$ the corresponding twisting functor, see [ 2, 18 ];

The action of the monoidal category $\mathcal{P}^\mathbb{Z}$ of graded projective functors on $\mathcal{O}_0^{\mathbb{Z}}$ categorifies the right regular $\textbf{H}$ -module.

2·6. R-polynomials

The isomorphism in (1) equips the algebra $\textbf{H}$ with the following $\mathbb{Z}[v,v^{-1}]$ -bases:

1. (1) $\{H_w=[\Delta_w]\,:\,w\in W\}$ , the standard basis;

2. (2) $\{\underline{H}_w=[P_w]\,:\,w\in W\}$ , the KL basis;

3. (3) $\{[\nabla_w]\,:\,w\in W\}$ , the costandard basis;

4. (4) $\{[L_w]\,:\,w\in W\}$ , the dual KL basis;

5. (5) $\{[I_w]\,:\,w\in W\}$ ;

6. (6) $\{[T_w]\,:\,w\in W\}$ .

The R-polynomials $\{r_{x,y}\,:\,x,y\in W\}$ are defined as the entries of the transformation matrix between the standard and the costandard bases, i.e.:

$$ [\Delta_y]=\sum_{x\in W}r_{x,y}[\nabla_x], \text{ for all } y\in W.$$

Note that $r_{x,y}\in\mathbb{Z}[v,v^{-1}]$ , by definition. For $x,y\in W$ and $k\in\mathbb{Z}$ , we denote by $r_{x,y}^{(k)}$ the coefficient at $v^k$ in $r_{x,y}$ .

As $\Delta_{w_0}=\nabla_{w_0}$ , we have

(2) \begin{equation}r_{x,w_0}=\begin{cases}1,& x=w_0;\\0,& \text{otherwise}.\end{cases}\end{equation}

For $w\in W$ and $s\in S$ such that $ws>w$ , we have

$$ [\theta_s\Delta_w]=v[\theta_s\Delta_{ws}]=[\Delta_{ws}]+v[\Delta_w]\,\text{ and }\,[\theta_s\nabla_w]=v^{-1}[\theta_s\nabla_{ws}]=[\nabla_{ws}]+v^{-1}[\nabla_w].$$

From this, we have the following recursive formula for R-polynomials: for $x,y\in W$ and $s\in S$ such that $ys<y$ , we have:

(3) \begin{equation}r_{x,ys}=\begin{cases}r_{xs,y},& xs>x;\\r_{xs,y}+ ({v-v^{-1}})r_{x,y},& xs<x.\end{cases}\end{equation}

Together, (2) and (3) determine the family of R-polynomials uniquely.

Please note that our indexing of R-polynomials differs from the usual one in [ 6, 17 ] by a $w_0$ -shift. For more information on R-polynomials, we refer to [ 17 ] and [ 6 , section 5·3].

2·7. Koszul and Koszul–Ringel dualities

Consider $\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$ the bounded derived category of $\mathcal{O}_0^{\mathbb{Z}}$ . The category $\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$ has a famous auto-equivalence called the Koszul duality and denoted by K, see [ 3, 23, 28 ]. It has the following properties:

1. (1) K sends $P_w$ to $L_{w^{-1}w_0}$ ;

2. (2) K sends $\Delta_w$ to $\nabla_{w^{-1}w_0}$ ;

3. (3) K sends $L_w$ to $I_{w^{-1}w_0}$ ;

4. (4) $\textrm{K}\langle j\rangle\cong [j]\langle -j\rangle\textrm{K}$ .

Another famous auto-equivalence of $\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$ is its Ringel self-duality given by the derived twisting functor $\mathcal{L}\top_{w_0}$ , see [ 29 ]. It has the following properties:

1. (1) $\mathcal{L}\top_{w_0}$ sends $P_w$ to $T_{w_0w}$ ;

2. (2) $\mathcal{L}\top_{w_0}$ sends $T_{w}$ to $I_{w_0w}$ ;

3. (3) $\mathcal{L}\top_{w_0}$ sends $\Delta_{w}$ to $\nabla_{w_0w}$ .

The composition $\textrm{RK}\;:\!=\;(\mathcal L\top_{w_0})^{-1}\circ\textrm{K}$ of the Koszul and Ringel self-dualities results in the Koszul–Ringel self-duality. We have $\textrm{RK}(\Delta_w)=\Delta_{w_0w^{-1}w_0}$ , and thus $\textrm{RK}^2(\Delta_w)=\Delta_w$ . Since $\{\Delta_w\}_{w\in W}$ generates $\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$ , it follows that the Koszul–Ringel self-duality is an involution. It has the following properties:

1. (1) RK sends $T_w$ to $L_{w_0w^{-1}w_0}$ ;

2. (2) RK sends $L_w$ to $T_{w_0w^{-1}w_0}$ ;

3. (3) RK sends $\Delta_w$ to $\Delta_{w_0w^{-1}w_0}$ ;

4. (4) RK sends $\nabla_w$ to $\nabla_{w_0w^{-1}w_0}$ .

We refer to [ 22 ] for further details.

A concrete realisation of this self-duality is via the category $\mathscr{LC}(T)$ of linear complexes of tilting objects is in $\mathcal{O}_0^{\mathbb{Z}}$ . Recall that a complex $\mathcal{T}_\bullet$ of tilting objects is called linear provided that each summand of each $\mathcal{T}_i$ has the form $T_w\langle i\rangle$ , for some $w\in W$ . The essence of the Koszul–Ringel self-duality is that RK restricts to an equivalence between the categories $\mathscr{LC}(T)$ and $\mathcal{O}_0^{\mathbb{Z}}$ where:

• (1) the tilting module $T_w$ (considered as a complex) is sent to the simple module $L_{w_0w^{-1}w_0}$ ;

• (2) the (linear!) complex of tilting modules representing $L_w$ is sent to the tilting module $T_{w_0w^{-1}w_0}$ ;

• (3) the linear tilting coresolution of $\Delta_w$ is sent to the module $\Delta_{w_0w^{-1}w_0}$ ;

• (4) the linear tilting resolution of $\nabla_w$ is sent to the module $\nabla_{w_0w^{-1}w_0}$ .

We use the notation $\mathcal{T}_\bullet(L_w)$ , $\mathcal{T}_\bullet(\Delta_w)$ and $\mathcal{T}_\bullet(\nabla_w)$ for the linear complexes of tilting modules that represent $L_w$ , $\Delta_w$ and $\nabla_w$ , for $w\in W$ , respectively.

3. Delorme formulae

3·1. Ungraded Delorme formula

The following result is proved in [ 11 ].

Proposition 1. For $x,y\in W$ , we have

$$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{Ext}^i_{\mathcal{O}}(\Delta_x,\Delta_y)=\delta_{x,y}.$$

Proof. First, we claim that, for any $M\in\mathcal{D}^b(\mathcal{O}_0)$ , we have the following relation in $\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0))$ :

(4) \begin{equation}[M]= \sum_{x\in W}\sum_{i\geq 0}(\!-\!1)^i\dim\textrm{Ext}^i_{\mathcal{O}}(\Delta_x,M)[\Delta_x].\end{equation}

Indeed, for $M=\nabla_y$ , this formula follows by combining the fact that standard and costandard modules in $\mathcal{O}_0$ are homologically orthogonal with the fact that $[\Delta_x]=[\Delta_x^\star]=[\nabla_x]$ , since $\star$ is simple preserving. For the general M, (4) now follows using the additivity of both sides with respect to distinguished triangles and the fact that costandard modules generate $\mathcal{D}^b(\mathcal{O}_0)$ .

The claim of the proposition is obtained from (4) by plugging in $M=\Delta_y$ and using that $\{[\Delta_x]\,:\,x\in W\}$ is a basis in $\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0))$ .

3·2. Graded Delorme formula

The following is a natural graded lift of Proposition 1. This statement explicitly explains the role which R-polynomials play in the theory of extensions between Verma modules.

Theorem 2. For $x,y\in W$ and $k\in\mathbb{Z}$ , we have:

$$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{ext}^i(\Delta_x\langle -k\rangle,\Delta_y)=r_{x,y}^{(k)}.$$

Proof. First, we claim that, for any $M\in\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$ , we have the following relation in $\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}}))$ :

(5) \begin{equation}[M]= \sum_{x\in W}\sum_{i\geq 0}\sum_{k\in\mathbb{Z}}(\!-\!1)^i\dim\textrm{ext}^i(\Delta_x\langle -k\rangle,M)[\nabla_x\langle -k\rangle].\end{equation}

Indeed, for $M=\nabla_y\langle m\rangle$ , this formula follows from the fact that standard and costandard modules in $\mathcal{O}_0^{\mathbb{Z}}$ are homologically orthogonal. For the general M, (5) now follows using the additivity of both sides with respect to distinguished triangles and the fact that costandard modules generate $\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$ .

The claim of the proposition is obtained from (5) by plugging in $M=\Delta_y$ and the definition of R-polynomials, since $[\nabla_x\langle-k\rangle]=v^k[\nabla_x]$ in $\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}}))$ .

4. General results

4·1. General setup

For $i,j\in\mathbb{Z}$ , $x,y\in W$ and $k\in\mathbb{Z}_{\geq 0}$ , set

$$ E(x,y,i,j,k)\;:\!=\;\dim\textrm{ext}^k(\Delta_x\langle i\rangle,\Delta_y\langle j\rangle).$$

An ultimate goal would be to find a formula for E(x,y,i,j,k). Let us start by listing some straightforward properties:

Proposition 3. For $i,j\in\mathbb{Z}$ , $x,y\in W$ and $k\in\mathbb{Z}_{\geq 0}$ , we have:

1. (a) $E(x,y,i,j,k)=E(x,y,i+a,j+a,k)$ , for all $a\in\mathbb{Z}$ ;

2. (b) $E(x,y,i,j,k)\neq 0$ implies $x\geq y$ ;

3. (c) $E(x,y,i,j,k)=E(w_0x^{-1}w_0,w_0y^{-1}w_0,-i,-j,k+j-i)$ ;

4. (d) $E(x,y,i,j,k)=E(x^{-1},y^{-1},-i,-j,k+j-i)$ ;

5. (e) $E(x,y,i,j,k)=E(w_0y,w_0x,-j,-i,k)$ .

Proof. Property (a) follows from the fact that the shift of grading is an auto-equivalence. Property (b) is a usual property of standard modules in highest weight categories. Property (c) follows from Koszul–Ringel duality. Property (d) follows from property (c) since conjugation by $w_0$ corresponds to an automorphism of the Dynkin diagram, which induces a(n highest weight) auto-equivalence on $\mathcal O_0$ . Property (e) follows by applying first $\mathcal{L}\top_{w_0}$ and then $\star$ .

Due to Proposition 3(a), we can consider the case $j=0$ . We define the Laurent polynomial ${\textrm{E}}_{x,y}(v,u)$ as follows:

$$ {\textrm{E}}_{x,y}(v,u)=\sum_{i\in\mathbb{Z}}\sum_{k\in\mathbb{Z}_{\geq 0}} E(x,y,k-i,0,k)v^{i}u^k.$$

Note that ${\textrm{E}}_{x,y}(v,u)$ is a polynomial in u and a Laurent polynomial in v. In fact, in Corollary 7 below, we will see that ${\textrm{E}}_{x,y}(v,u)$ is also a polynomial in v.

Here we have ${\textrm{E}}_{x,y}(v, -v^{-1})=r_{x,y}(v)$ , and Proposition 3 is expressed as follows.

Proposition 4. We have:

1. (a) ${\textrm{E}}_{x,y} = 0$ unless $y\leq x$ .

2. (b) ${\textrm{E}}_{x,y}(u,v) = \textrm{E}_{w_0y^{-1}w_0,w_0x^{-1}w_0}(v,u)$ .

3. (c) ${\textrm{E}}_{x,y}(u,v) =\textrm{E}_{y^{-1},x^{-1}}(v,u)$ .

4. (d) ${\textrm{E}}_{x,y}(v,u)=\textrm{E}_{w_0y,w_0x}(v,u)$ .

4·2. Bounds in terms of KL polynomials

Proposition 5. For $x,y\in W$ we have

(6) \begin{equation} \sum_{a,b\in\mathbb Z} \dim\hom(\Delta_x\langle b-a \rangle,\mathcal T_b(\Delta_y))v^a u^{b} = \sum_{z\in W} p_{x w_0,z w_0}(v) p_{y,z}(u).\end{equation}

(Note that the summand $ p_{x w_0,z w_0}(v) p_{y,z}(u)$ is zero unless $y\leq z\leq x$ .)

Proof. The Koszul–Ringel duality gives

(7) \begin{equation} [\Delta_{w_0y^{-1} w_0}\;:\;L_{w_0z^{-1} w_0}\langle -b\rangle] = [\mathcal{T}_\bullet(\Delta_y)\;:\;T_z\langle b \rangle[\!-\!b] ].\end{equation}

The left-hand side is, by the BGG reciprocity, equal to $[P_{w_0z^{-1} w_0}\;:\;\Delta_{w_0y^{-1} w_0}\langle -b\rangle]$ . It follows that

(8) \begin{equation} \sum_b[\mathcal{T}_\bullet(\Delta_y)\;:\;T_z\langle b \rangle[\!-\!b] ]u^b = p_{w_0y^{-1} w_0,w_0z^{-1} w_0}(u) = p_{y,z}(u).\end{equation}

On the other hand, for each $z\in W$ , we have

\begin{equation*}\dim \hom(\Delta_x,T_z\langle a\rangle) = [T_z \;:\; \nabla_x\langle -a\rangle] =[T_{w_0zw_0} \;:\; \nabla_{w_0xw_0}\langle -a\rangle] = [P_{z w_0}\;:\;\Delta_{x w_0}\langle -a\rangle],\end{equation*}

where we apply the automorphism induced by conjugation by $w_0$ in the second equality and the Ringel duality in the third equality, and thus

(9) \begin{equation} \sum_a \dim \hom(\Delta_x,T_z\langle a\rangle)v^a = p_{x w_0,z w_0}(v).\end{equation}

Combining (9) and (8), we obtain the claimed equation.

Given $p,q\in \mathbb Z[u^{\pm1},v^{\pm1}]$ , we write $p\leq q$ if all coefficients of $q-p$ are non-negative.

Corollary 6. For $x,y\in W$ we have

(10) \begin{equation} \textrm{E}_{x,y}(v,u)\leq \sum_{z\in W} p_{x w_0,z w_0}(v) p_{y,z}(u). \end{equation}

Proof. Since the space $\operatorname{ext}^b(\Delta_x\langle b-a\rangle,\Delta_y)$ is computed as the homology of the complex $\hom(\Delta_x\langle b-a \rangle [\!-\!b],\mathcal{T}_\bullet(\Delta_y))$ at the homological position 0, the claim follows from Proposition 5.

Corollary 7. We have ${\textrm{E}}_{x,y}\in \mathbb Z[u,v]$ . Moreover, for $x\geq y$ , we have:

1. (a) $\deg_u {\textrm{E}}_{x,y} = \ell(x)-\ell(y)$ ;

2. (b) $\deg_v {\textrm{E}}_{x,y} = \ell(x)-\ell(y)$ ;

3. (c) $\deg {\textrm{E}}_{x,y} = \ell(x)-\ell(y)$ ;

4. (d) the degree of each monomial appearing in ${\textrm{E}}_{x,y}$ has the same parity as $\ell(x)-\ell(y)$ ,

where $\deg_u,\deg_v$ denote the degrees with respect to the variables u,v, respectively. In fact, the coefficients of ${\textrm{E}}_{x,y}(u,v)$ at $u^{\ell(x)-\ell(y)}$ and at $v^{\ell(x)-\ell(y)}$ are both 1.

Proof. Since $p_{w,w'}(\upsilon)\in\mathbb Z_{\geq 0}[\upsilon]$ with the parity vanishing property and $\deg p_{w,w'} = \ell(w')-\ell(w)$ for all $w,w'\in W$ with $w\leq w'$ (see Subsection 2·4), Corollary 6 provides the first statement, the inequality “ $\leq$ ” in all three numbered claims, and (d). To have “ $=$ ” in the numbered claims, it is enough to prove the last remark. But the coefficients of ${\textrm{E}}_{x,y}(u,v)$ at $u^{\ell(x)-\ell(y)}$ and at $v^{\ell(x)-\ell(y)}$ are the same by Proposition 3(c), where the former is the dimension of $\hom(\Delta_x\langle {\ell(y)-\ell(x)}\rangle,\Delta_y)$ . The latter space consists of the unique inclusion between Verma modules (see Subsection 2·3), and thus has dimension one. This completes the proof.

Corollary 8. If $E(x,y,i,0,k)\neq 0$ for $x\geq y$ , then

1. (a) $0\leq k\leq \ell(x)-\ell(y)$ ;

2. (b) $2k+\ell(y)-\ell(x)\leq i\leq k$ ;

3. (c) if $k=0$ , then $i=\ell(y)-\ell(x)$ ;

4. (d) if $k=i$ , then $k=i=\ell(x)-\ell(y)$ ;

5. (e) $\ell(y)-\ell(x)-i$ is even.

Thus, each (k,i) with nonzero E(x,y,i,0,k) is in the dark grey region in Figure 1.

Proof. The claims are exactly the claims in Corollary 7 via the change of variables.

The bound given in Corollary 6 does not take into account the differentials in the complex of homomorphisms between $\Delta_y$ and $\mathcal{T}_\bullet(\Delta_x)$ and can be lowered in various ways. We record one such strenghtening of the bound.

Proposition 9. Let $x,y\in W$ be such that $x\geq y$ . Then, for $k\in\mathbb{Z}_{\geq 0}$ and $i\in\mathbb{Z}$ such that $2k-i\neq \ell(x)-\ell(y)$ , we have:

\begin{equation*}E(x,y,i,0,k)\leq\sum_{w\in W}p^{(k)}_{w_0y^{-1}w_0,w_0w^{-1}w_0}p_{w_0x,w_0w}^{(k-i)}-\max_{\ell(w)=\ell(y)+k, w\geq y}p_{w_0x,w_0w}^{(k-i)}.\end{equation*}

Proof. Let $w\in W$ such that $w\geq y$ and $\ell(w)=\ell(y)+k$ . Via Koszul–Ringel duality, the inclusion $\Delta_{w_0w^{-1}w_0}\langle k\rangle\hookrightarrow\Delta_{w_0y^{-1}w_0}$ gives an injective (component-wise) homomorphism of complexes $\mathcal{T}_\bullet(\Delta_w)\langle -k\rangle[k]\hookrightarrow\mathcal{T}_\bullet(\Delta_y)$ .

Since each hom space between Verma modules is concentrated in one degree, any nonzero homomorphism, say $\phi\;:\;\Delta_x\langle i \rangle \to T_w=\mathcal T_0(\Delta_w)$ does not give rise to a homomorphism of complexes, that is, $d \circ \phi\neq 0$ , where d is (the restriction of) the differential in $\mathcal{T}_\bullet(\Delta_w)$ .

Since $\mathcal{T}_\bullet(\Delta_w)\langle -k\rangle[k]$ is a subcomplex of $\mathcal{T}_\bullet(\Delta_y)$ , we still have $d\circ \phi\neq 0$ when d is the differential in $\mathcal{T}_\bullet(\Delta_y)$ . Hence $\phi$ does not contribute to an (appropriately shifted) extension from $\Delta_x$ to $\Delta_y$ . The claim follows.

4·3. The exact information given by the R-polynomials

Theorem 2 implies that the coefficient $r_{x,y}^{(i)}$ of the R-polynomial $r_{x,y}$ has the following interpretation in terms of the dark grey triangle in Figure 1. We need to consider the integral points in the intersection of the line $b=i$ with the dark grey triangle (the dashed parts excluded) as given by the small black boxes in the following picture:

The coefficient $r_{x,y}^{(i)}$ is exactly the alternating sum of the dimensions of those extensions from (a shift of) $\Delta_x$ to $\Delta_y$ , where the top of $\Delta_x$ is shifted by the coordinates of these small black boxes. Note that the dashed sides are excluded, except for the south and the east vertices of the triangle.

4·4. Consequences

Corollary 10. Let $\ell(x)-\ell(y)\equiv i\mod 2$ . If the intersection of the line $b=i$ with the dark grey triangle contains exactly one integral point, say $(-a,b)$ , then

(11) \begin{equation}a=\frac{i+\ell(x)-\ell(y)}{2}\quad\text{ and }\quad\dim\textrm{ext}^{a}(\Delta_x\langle i\rangle,\Delta_y)=|r_{x,y}^{(-i)}|.\end{equation}

Proof. This follows directly from the discussion in Subsection 4·3.

Corollary 11. Let $x,y\in W$ with $x\geq y$ . Then (11) holds for the following values of i:

$$ i\in\{\ell(x)-\ell(y),\ell(x)-\ell(y)-2,2-\ell(x)+\ell(y),\ell(y)-\ell(x)\}.$$

Proof. If $i=\ell(x)-\ell(y)$ , then the intersection of $b=i$ with the dark grey triangle consists of the east vertex of the triangle. If $i=\ell(y)-\ell(x)$ , then the intersection of $b=i$ with the dark grey triangle consists of the south vertex of the triangle. If $i=\ell(x)-\ell(y)-2$ , then the intersection of $b=i$ with the dark grey triangle consists of the vertices $(\ell(y)-\ell(x)+1,\ell(x)-\ell(y)-2)$ and $(\ell(y)-\ell(x)+2,\ell(x)-\ell(y)-2)$ , however, the latter one belongs to the dashed line. Similarly, if $i=\ell(y)-\ell(x)+2$ , then the intersection of $b=i$ with the dark grey triangle consists of the vertices $(\!-\!1,\ell(y)-\ell(x)+2)$ and $(0,\ell(y)-\ell(x)+2)$ , however, the latter one belongs to the dashed line.

This means that, in all four cases, we have exactly one relevant integral point. Now the claim follows from Corollary 10.

Corollary 12. Let $x,y\in W$ with $x\geq y$ . If $\ell(x)-\ell(y)\leq 3$ , then (11) holds.

Proof. The claim of the corollary follows directly from Corollary 11 since, under the assumption $\ell(x)-\ell(y)\leq 3$ , the values of i listed in Corollary 11 cover all possibilities for potentially non-zero extensions.

4·5. Expected vs additional extensions

As illustrated in Figure 1, the proof of Proposition 5 implies that the non-zero E(x,y,i,0,k) split naturally into two types:

1. (1) The cases when $k={i+\ell(x)-\ell(y)}/{2}$ , i.e., the top of $\Delta_x\langle i\rangle$ lies on the solid dark grey side of the dark grey triangle. We call such cases expected.

2. (2) All other cases. In these cases the top of $\Delta_x\langle i\rangle$ belongs to the interior of the dark grey triangle. We call such cases additional.

Then the discussion in Subsection 4·3 gives the following statement.

Corollary 13. If $x,y\in W$ and $i\in\mathbb{Z}$ are such that all extensions between $\Delta_x\langle i\rangle$ and $\Delta_y$ are known to be expected, then (11) holds.

Each non-zero element in $\textrm{ext}^k(\Delta_x\langle i\rangle,\Delta_y)$ is realised via a non-zero homomorphism from $\Delta_x\langle i\rangle$ to $\mathcal{T}_{k}(\Delta_y)$ . Since the latter has a standard filtration and all non-zero morphisms between standard modules are injective, the map from $\Delta_x\langle i\rangle$ to $\mathcal{T}_{k}(\Delta_y)$ must be injective, in particular, it must be injective when restricted to the simple socle of $\Delta_x\langle i\rangle$ .

For expected extensions, the socle of $\Delta_x\langle i\rangle$ is on the diagonal side of the light gray triangle. This means that the homomorphism from $\Delta_x\langle i\rangle$ to $\mathcal{T}_{k}(\Delta_y)$ which realises this extension has an image inside the direct sum of all $T_w\langle k\rangle$ , where the sum is taken over all w such that $w\geq y$ and $\ell(w)=\ell(y)+k$ .

For additional extensions, the socle of $\Delta_x\langle i\rangle$ is in the interior of the light gray triangle. This means that the homomorphism from $\Delta_x\langle i\rangle$ to $\mathcal{T}_{k}(\Delta_y)$ which realises this extension:

1. (1) either induces a non-zero map to a summand of $\mathcal{T}_{k}(\Delta_y)$ different from the $T_w\langle k\rangle$ as in the previous paragraph;

2. (2) or induces a non-zero map to some $T_w\langle k\rangle$ as in the previous paragraph, in which case the socle of this $T_w\langle k\rangle$ is not simple and this induced map maps the socle of $\Delta_x\langle i\rangle$ to the socle part of $T_w\langle k\rangle$ which lives in a non-maximal degree.

Each of these cases is only possible in the situation when some KL-polynomials are nontrivial.

The first situation is possible only if $\mathcal{T}_{k}(\Delta_y)$ contains a summand $T_w\langle k\rangle$ , for some $w\geq y$ which violates $\ell(w)=\ell(y)+k$ . Via the Koszul–Ringel duality, the fact that $T_w\langle k\rangle$ is a summand of $\mathcal{T}_{k}(\Delta_y)$ means that $[\Delta_{w_0y^{-1}w_0}\;:\;L_{w_0w^{-1}w_0}\langle -k\rangle]\neq 0$ . The latter multiplicity is exactly the coefficient at $v^k$ in the KL polynomial $p_{w_0y^{-1}w_0,w_0w^{-1}w_0}$ . Since $\ell(w)\neq \ell(y)+k$ , this means that $p_{w_0y^{-1}w_0,w_0w^{-1}w_0}$ is not trivial.

The second situation is possible only if the socle of some $T_w\langle k\rangle$ , where $w\geq y$ and $\ell(w)=\ell(y)+k$ , is not simple. Since the socle is a direct sum of $L_{w_0}$ , the latter is if and only if $(T_w\;:\;\Delta_{w_0})>1$ , which is equivalent, via Koszul duality, to the polynomial $p_{e,w_0w}$ being nontrivial.

An immediate corollary of this discussion is the following.

Corollary 14. Let $y\in W$ be such that $p_{w_0y^{-1}w_0,w_0w^{-1}w_0}$ and $p_{e,w_0w}$ are trivial, for all $w\geq y$ . Then (11) holds for all $x\in W$ such that $x\geq y$ .

Proof. By the assumption on trivial KL polynomials, the only non-zero extensions between Verma modules are those where the top of $\Delta_x\langle i\rangle$ is on the solid dark grey side of the dark grey triangle. Therefore (11) follows from Theorem 2.

The assumption of Corollary 14 is satisfied for all $y\in W$ if W is of rank 2. We thus obtain the following.

Corollary 15. (11) holds in all cases when W has rank 2.

Remark 16. If W is of rank 2, a closed formula for the R-polynomials makes Corollary 15 more explicit. For $x,y\in W$ , letting $d = \ell(y)-\ell(x)$ , we have

(12) \begin{equation} r_{y,x} = v^{d} - 2v^{d-2} + 2v^{d-4} -\cdots +(\!-\!1)^{d-1} 2v^{-d+2} +(\!-\!1)^{d} v^{-d}.\end{equation}

One way to see (12) is to directly compute the base change between the costandard and the standard bases, that is, by combining the equations

\begin{equation*}[\Delta_x] = \sum_{z\geq x}[L_z\langle \ell(x)-\ell(z)\rangle]\end{equation*}

and

\begin{equation*} [L_z] = \sum_{y\geq z}(\!-\!1)^{\ell(y)-\ell(z)} [\nabla_y\langle \ell(y)-\ell(z)\rangle]\end{equation*}

well known in the types of rank 2. The coefficients $1,2,\cdots,2,1$ in (12) reflect the shape of the Bruhat interval [x,y] in the dihedral group W.

Therefore, Corollary 15 says that the graded extension between Verma modules are one dimensional in the extremes and two dimensional in the middle (along the solid dark grey side of the expected extensions). The latter result was previously obtained in [ 13 , theorem 1·1].

4·6. Koszulity

Denote by $\mathscr{D}$ the full subcategory of the derived category $\mathcal{D}(\mathcal{O}_0^\mathbb{Z})$ given by the objects $\Delta_w\langle i\rangle[j]$ , where $w\in W$ and $i,j\in\mathbb{Z}$ such that

$$ i\in\{-\ell(w)-2j,-\ell(w)-2j-1\}.$$

Note that the shift put the socle of each $\Delta_w\langle i\rangle[j]$ in the “generating diagonal” $i\in\{-2j,-2j+1\}$ . The group $\mathbb{Z}$ acts freely on $\mathscr{D}$ by sending $\Delta_w\langle i\rangle[j]$ to $\Delta_w\langle i-2m\rangle[j+m]$ , for $m\in\mathbb{Z}$ .

Consider the category $\mathscr{D}$ -mod of finite dimensional $\mathscr{D}$ -modules. The objects of this category are $\mathbb{C}$ -linear functors M from $\mathscr{D}$ to vector spaces (over $\mathbb{C}$ ) such that the sum, over all $\texttt{i}\in \mathscr{D}$ , of the dimensions of $\textrm{M}(\texttt{i})$ is finite. The morphisms in $\mathscr{D}$ -mod are natural transformations of functors.

The following results generalizes [ 14 , theorem 5·1] (see also Theorem 31). Theorem 20 below shows a case that is covered by Theorem 31 but not by [ 14 , theorem 5·1].

Theorem 17. Assume that all extensions between the Verma modules in $\mathcal{O}_0$ are expected. Then the following assertions hold:

1. (a) we have an equivalence $\mathcal{D}^*(\mathcal{O}_0^\mathbb{Z})\cong \mathcal{D}^*(\mathscr{D}\text{-}\textrm{mod})$ where $*\in\{b,\uparrow,\downarrow\}$ ;

2. (b) the path algebra of $\mathscr{D}$ is Koszul and is Koszul self-dual.

Proof. The proof essentially follows the proof of [ 14 , theorem 5·1].

The assumption that all extensions between the Verma modules in $\mathcal{O}_0^{\mathbb{Z}}$ are expected says exactly that $\mathscr{D}$ has no self-extensions (of a nonzero degree). Since $\mathscr{D}$ generates $\mathcal{D}^b(\mathcal{O}_0^\mathbb{Z})$ , the subcategory $\mathscr{D}$ gives rise to a tilting complex in the sense of Rickard (see [ 14 , subsection 2·1], where such $\mathscr{D}$ is called a tilting subset). Therefore, claim (a) follows from the Rickard-Morita Theorem (see [ 14 , theorem 2·1]).

To show claim (b), we note that the equivalence $\mathcal{D}^*(\mathcal{O}_0^\mathbb{Z})\to \mathcal{D}^*(\mathscr{D}\text{-}\textrm{mod})$ is given by $X \mapsto \textrm{Hom}_{\mathcal D^{*}(\mathcal O_0^{\mathbb{Z}})}(-,X)$ where the latter functor is restricted to $\mathscr D$ . Since the Verma modules and the dual Verma modules are homologically orthogonal, simple objects in $\mathscr{D}$ -mod correspond to dual Verma modules under the equivalence. From these we see that the quadratic dual of $\mathscr{D}$ consists of the dual Verma modules, with the similar shifts (the tops on the generating diagonal), and that the composition

\begin{equation*} \mathcal{D}^\uparrow(\mathscr{D}\text{-}\textrm{mod})\xrightarrow{\cong}\mathcal{D}^\uparrow(\mathcal{O}_0^\mathbb{Z})\xrightarrow[\cong]{-^*} \mathcal{D}^\downarrow(\mathcal{O}_0^\mathbb{Z})\xrightarrow{\cong} \mathcal{D}^\downarrow(\mathscr{D}\text{-}\textrm{mod}),\end{equation*}

where the first and the third functors are from (a) and the middle functor is the simple preserving duality, agrees with the Koszul duality functor. Thus both the Koszulity and the Koszul self duality follow from [ 23 , theorem 30].

5. Combinatorics of Bruhat intervals

5·1. Equivalence classes of Bruhat intervals

Denote by $\mathscr{I}$ the set of all pairs $(x,y)\in W^2$ such that $x\geq y$ . Each such pair (x,y) determines uniquely an interval in the Bruhat order, denoted $[y,x]=\{z\in W\,:\, y\leq z\text{ and }z\leq x\}$ . Let $\sim$ denote the minimal equivalence relations on $\mathscr{I}$ that contains all $(x,y)\sim (xs,ys)$ , where $s\in S$ is such that $\ell(x)>\ell(xs)$ and $\ell(y)>\ell(ys)$ , and all $(x,y)\sim (sx,sy)$ , where $s\in S$ is such that $\ell(x)>\ell(sx)$ and $\ell(y)>\ell(sy)$ .

Proposition 18. If $(x,y)\sim(x',y')$ , then ${\textrm{E}}_{x,y}=\textrm{E}_{x',y'}$ .

Proof. In case $(x',y')=(sx,sy)$ , for some $s\in S$ such that $\ell(x)>\ell(sx)$ and $\ell(y)>\ell(sy)$ , we apply $\mathcal{L}\top_s$ . It sends $\Delta_{sx}$ to $\Delta_x$ and $\Delta_{sy}$ to $\Delta_y$ . On top of that, $\mathcal{L}\top_s$ is a derived equivalence and thus induces the necessary isomorphisms between the extension spaces.

In case $(x',y')=(xs,ys)$ , for some $s\in S$ such that $\ell(x)>\ell(xs)$ and $\ell(y)>\ell(ys)$ , we can apply the derived equivalence $\mathcal{L}\textsf{C}_s$ and argue similarly to the previous paragraph. The claim follows.

Note that $(x,y)\sim(x',y')$ does not imply a poset isomorphism between the Bruhat intervals [y,x] and [y’,x’] in general. For example, in type $A_3$ with simple reflections r,s,t representing the following nodes of the Dynkin diagram: , we obviously have $(rts,e)\sim(srts,s)$ . However, the boolean interval [e,rts] is not poset isomorphic to the interval [s,srts]. In fact, they even have different characters as graded posets.

5·2. Boolean and coboolean elements

Recall that an element $w\in W$ is called boolean provided it is a multiplicity-free product of simple reflections. The name is justified by the observation that the Bruhat ideal [e,w], for a boolean element w, is isomorphic, as a poset, to the poset of subsets of the set of simple reflections appearing in w.

Proposition 19. Let $x',y'\in W$ be such that $x'\geq y'$ .

1. (a) Assume that the equivalence class of (x’,y’) contains some (x,y) with x boolean. Then $\textrm{ext}^k(\Delta_{x'}\langle i\rangle,\Delta_{y'})$ is given by (11).

2. (b) Assume that the equivalence class of (x’,y’) contains some (x,y) with $w_0y$ boolean. Then $\textrm{ext}^k(\Delta_{x'}\langle i\rangle,\Delta_{y'})$ is given by (11).

Proof. The two claims of the proposition are connected by the Ringel duality and the simple preserving duality $^\star$ , so it is enough to prove claim (b). By Proposition 18, it is enough to consider the case $x=x'$ and $y=y'$ , i.e., $w_0y$ is boolean. (Note that the latter is if and only if $yw_0$ is boolean.) We claim that, in this case, all KL polynomials $p_{xw_0,zw_0}$ and $p_{y,z}$ , where $y\leq z\leq x$ , are trivial. This and Proposition 5 proves (b).

The claim is a well-known property of KL polynomials (see [ 6 , exercise 5·36.(e)]), which is proved, for example, as follows. If w is boolean, say $w=st\cdots u$ for $s,t,\cdots,u\in S$ distinct, then the KL basis element is of the form $\underline{H}_w=\underline{H}_s\underline{H}_t\cdots \underline{H}_u$ . So all KL polynoimals $p_{w',w}$ , for $w'\leq w$ , are trivial, and so are $p_{w_0w'w_0,w_0ww_0}$ . By Kazhdan–Lusztig inversion formula (see [ 17 , section 3]), the same is true for $p_{w_0w,w_0w'}$ and $p_{ww_0,w'w_0}$ . These include all $p_{xw_0,zw_0}$ and $p_{y,z}$ since $zw_0\leq yw_0$ is boolean.

6. Special cases

6·1. Type $A_1$

In type $A_1$ , we have $W=\{e,s\}$ . The only non-zero extension of positive degree between Verma modules is $\textrm{ext}^1(\Delta_s\langle 1\rangle,\Delta_e)\cong \mathbb{C}$ realised in the projective module $P_s$ . Here is the table for $\textrm{E}_{x,y}(v,u)$ :

6·2. Type $A_2$

In type $A_2$ , we have $W=\{e,s,t,st,ts,w_0=sts=tst\}$ . By Corollary 15, all extensions between Verma modules in this case are given by (11) via the coefficients of R-polynomials. Here is the table for the R-polynomials in this case:

Here is the table for E-polynomials in this case:

6·3. Type $A_3$

In type $A_3$ , the group W is generated by the simple reflections r,s,t representing the following nodes of the Dynkin diagram: . Our main result in this subsection is the following.

Theorem 20. In type $A_3$ , all extensions between Verma modules in $\mathcal{O}_0$ are expected and given by (11).

Please note that Theorem 20 does not claim that, in type $A_3$ , we are always in the situation as described by the assumptions of Corollary 10. The claim is that, regardless whether the assumptions of Corollary 10 hold, all extensions between Verma modules are given by (11).

Proof. In type $A_3$ , there are two non-trivial KL-polynomials of the form $p_{e,w}$ , namely:

$$ p_{e,srts}=v^2+v^4\quad\text{ and }\quad p_{e,rstsr}=v^3+v^5.$$

This implies the following two facts:

The minimal tilting coresolution $\mathcal{T}_\bullet(\Delta_e)$ , apart from the “expected” summands $T_w\langle\ell(w)\rangle[\!-\!\ell(w)]$ , where $w\in S_4$ , also has two additional summands: $T_{srts}\langle 2\rangle[\!-\!2]$ and $T_{rstsr}\langle 3\rangle[\!-\!3]$ .

Figure 2. Dimensions of socles for summands of $\mathcal{T}_\bullet(\Delta_e)$

The following tilting modules have non-simple socle:

1. (1) the module $T_{s}$ , whose expected part of the socle is $L_{w_0}\langle -\ell(w_0s)\rangle$ , has additional socle $L_{w_0}\langle -\ell(w_0s)+2\rangle$ ,

2. (2) the module $T_{rt}$ , whose expected part of the socle is $L_{w_0}\langle -\ell(w_0rt)\rangle$ , has additional socle $L_{w_0}\langle -\ell(w_0rt)+2\rangle$ .

Every $T_w$ not listed above has socle $L_{w_0}\langle -\ell(w_0w)\rangle$ . We can now collect the information about the socles of all tilting summands appearing in $\mathcal{T}_\bullet(\Delta_e)$ in Figure 2. Here the expected hom dimension between $L_{w_0}=\Delta_{w_0}$ and each $\mathcal T_i(\Delta_e)$ is marked by a circle and the additional part is marked by squares. The four additional dimensions come from the above list:

1. (1) the additional socle of $T_{s}\langle 1\rangle[\!-\!1]$ gives one dimension at the point $(\!-\!1,-2)$ ;

2. (2) the additional socle of $T_{rt}\langle 2\rangle[\!-\!2]$ gives one dimension at the point $(\!-\!2,0)$ ;

3. (3) the socle of the additional summand $T_{srts}\langle 2\rangle[\!-\!2]$ gives one dimension at the point $(\!-\!2,0)$ ;

4. (4) the socle of the additional summand $T_{rstsr}\langle 2\rangle[\!-\!2]$ gives one dimension at the point $(\!-\!3,2)$ .

The aim is to show that no homomorphism in a square space gives rise to a nonzero homomorphism of complexes between the corresponding shifts of $L_{w_0}$ and $\mathcal{T}_\bullet(\Delta_e)$ . From this it follows that there is no additional homomorphism of complexes (i.e., no homomorphism of complexes that possibly gives an additional extension) between $\Delta_x$ and $\mathcal{T}_\bullet(\Delta_e)$ since the latter would restrict to a homomorphism from the socle $L_{w_0}$ (see also the socle discussion in Subsection 4·5).

By Proposition 9, the additional socle of $T_{s}\langle 1\rangle[\!-\!1]$ does not contribute to a homomorphism of complexes from $L_{w_0}\langle 1\rangle[\!-\!2]$ to $\mathcal{T}_\bullet(\Delta_e)$ . This means that there are no additional first extensions to $\Delta_e$ (this is a general fact, see [ 21 , theorem 32]) from any Verma modules. Therefore the additional dimension 1 at the point $(\!-\!1,-2)$ decreases the value 5 at the point $(\!-\!2,-2)$ by 1, resulting in the dimension 4.

By Koszul–Ringel duality, the fact that we have $\textrm{ext}^1(\Delta_{w_0}\langle -2\rangle,\Delta_e)=0$ implies that we have $\textrm{ext}^3(\Delta_{w_0}\langle 2\rangle,\Delta_e)=0$ . Therefore, any homomorphism of complexes from $\Delta_{w_0}\langle 2\rangle[\!-\!3]$ to $\mathcal{T}_\bullet(\Delta_e)$ is homotopic to zero. Since no homotopies between these two complexes are possible (as $\textrm{hom}(\Delta_{w_0}\langle 2\rangle,\mathcal{T}_2(\Delta_e))=0$ ), it follows that the composition of the differential in $\mathcal{T}_\bullet(\Delta_e)$ homomorphism $\Delta_{w_0}\langle 2\rangle \to \mathcal{T}_3(\Delta_e)$ is non-zero. Therefore the only relevance of the additional dimension 1 at the point $(\!-\!3,2)$ is that it decreases the value 5 at the point $(\!-\!4,2)$ by 1 resulting in 4, which is a coefficients of the R-polynomial.

It remains to deal with the square point $(\!-\!2,0)$ . Similarly to the above, using Proposition 9, we obtain that the restriction of the differential in $\mathcal{T}_\bullet(\Delta_e)$ to the additional socle of $T_{rt}\langle 2\rangle[\!-\!2]$ is non-zero. This takes care of one dimension at the square point $(\!-\!2,0)$ . The second dimension at this point corresponds to the usual (simple) socle of the additional summand $T_{srts}\langle 2\rangle[\!-\!2]$ . We now argue that the image of the restriction of the differential in $\mathcal{T}_\bullet(\Delta_e)$ to this socle component is linearly independent to the image of the restriction of the differential in $\mathcal{T}_\bullet(\Delta_e)$ to the additional socle of $T_{rt}\langle 2\rangle[\!-\!2]$ .

Our argument is very much ad hoc, we use the explicit description of $\Delta_e$ as given in [ 31 , appendix A]. From it we see that the differential in $\mathcal{T}_\bullet(\Delta_e)$ restricts to a non-zero map from $T_{srts}\langle 2\rangle[\!-\!2]$ to $T_{sts}\langle 3\rangle[\!-\!3]$ and, at the same time, this differential restricts to the zero map from $T_{rt}\langle 2\rangle[\!-\!2]$ to $T_{sts}\langle 3\rangle[\!-\!3]$ . It remains to show that any non-zero map from $T_{srts}\langle 2\rangle[\!-\!2]$ to $T_{sts}\langle 3\rangle[\!-\!3]$ is injective (i.e., does not kill the socle). Since the domain has a standard filtration and the codomain has a costandard filtration, a non-zero map from $T_{srts}\langle 2\rangle[\!-\!2]$ to $T_{sts}\langle 3\rangle[\!-\!3]$ must be a linear combination of maps lifted from some standard subquotient of $T_{srts}\langle 2\rangle[\!-\!2]$ to some costandard subquotient of $T_{sts}\langle 3\rangle[\!-\!3]$ . There is only one such pair which appears with correct shifts: $\Delta_{srts}\langle 2\rangle[\!-\!2]$ for $T_{srts}\langle 2\rangle[\!-\!2]$ and $\nabla_{srts}\langle 2\rangle[\!-\!2]$ for $T_{sts}\langle 3\rangle[\!-\!3]$ . Therefore, a non-zero homomorphism from $T_{srts}\langle 2\rangle[\!-\!2]$ to $T_{sts}\langle 3\rangle[\!-\!3]$ is a lift of a homomorphism from $\Delta_{srts}\langle 2\rangle[\!-\!2]$ to $T_{sts}\langle 3\rangle[\!-\!3]$ . Since any homomorphism from a Verma module to a tilting module is injective, a non-zero map from $\Delta_{srts}\langle 2\rangle[\!-\!2]$ to $T_{sts}\langle 3\rangle[\!-\!3]$ is injective. Since the socles of $T_{srts}\langle 2\rangle[\!-\!2]$ and $\Delta_{srts}\langle 2\rangle[\!-\!2]$ coincide, we get the claim.

The arguments above show that, in the category of complexes, the only homomorphisms from Verma modules to $\mathcal{T}_\bullet(\Delta_e)$ are with expected shifts. Since all $\mathcal{T}_\bullet(\Delta_y)$ are subcomplexes of $\mathcal{T}_\bullet(\Delta_e)$ (up to some shifts in both homological and grading), it follows that the only possible extensions between Verma modules are expected extensions. The fact that they are given by (11) follows from the graded Delorme formula. This completes the proof.

6·4. Some first extensions between Verma modules in type A

In this subsection we use the results of [ 19 ] to construct many additional first extensions between Verma modules in type A. We refer to [ 19 ] for the details of the facts recalled below. We assume that $W=S_n$ with the Dynkin diagram

For $i,j\in\{1,2,\dots,n-1\}$ , we denote by $\hat{w}_{i,j}$ the following element:

$$ \hat{w}_{i,j}=\begin{cases}s_is_{i-1}\dots s_j,& j\leq i;\\s_is_{i+1}\dots s_j,& j> i.\end{cases}$$

Note that $\hat{w}_{i,i}=s_i$ . By construction, $\hat{w}_{i,j}$ has left descent $s_i$ and right descent $s_j$ . We also denote by $w_{i,j}$ the element $\hat{w}_{i,n-j}w_0$ . Dually, the element $w_{i,j}$ has left ascent $s_i$ and right ascent $s_j$ . The set $\{w_{i,j}\}$ is exactly the penultimate two-sided KL cell in $S_n$ .

Each simple $L_{w_{i,j}}$ is graded multiplicity-free in $\Delta_e$ . In fact, $[\Delta_e\;:\;L_{w_{i,j}}\langle -m\rangle]=1$ if and only if $m\in\{\ell(w_{i,j}),\ell(w_{i,j})-2,\ell(w_{i,j})-4,\dots,\ell(w_{i,j})-2q_{i,j}\}$ where

$$ q_{i,j}=\min\{n-1-i,n-1-j,i-1,j-1\}.$$

Note that the ungraded multiplicity of $L_{w_{i,j}}$ in $\Delta_e$ equals $1+q_{i,j}$ .

Recall that an element of $S_n$ is called bigrassmannian provided that it has a unique left descent and a unique right descent (for example, all $\hat{w}_{i,j}$ are bigrassmannian). There are exactly $1+q_{i,j}$ bigrassmannian elements in $S_n$ with left descent $s_i$ and right descent $s_j$ . They form a chain with respect to the Bruhat order and hence are in natural bijection, denoted $\Phi_{i,j}$ , with the graded simple subquotients of $\Delta_e$ isomorphic, up to a shift, to $L_{w_{i,j}}$ (ordered by increasing graded shifts). In particular, the element $\hat{w}_{i,j}$ corresponds to $L_{w_{i,j}}\langle -(\ell(w_{i,j})-2q_{i,j})\rangle$ .

For $w\in S_n$ , denote by $\textbf{BM}_w$ the set of all Bruhat maximal elements in the set of all bigrassmannian elements of the Bruhat interval [e,w].

Proposition 21. Let $w\in S_n$ and let $u\in \textbf{BM}_w$ have left descent $s_i$ and right descent $s_j$ . If $\Phi_{i,j}(u)=L_{w_{i,j}}\langle m\rangle$ and $w_{i,j}\geq w$ , then $\textrm{ext}^1(\Delta_{w_{i,j}}\langle m\rangle,\Delta_{w})\neq 0$ .

Proof. Applying $\textrm{hom}({}_-, \Delta_{w})$ to the short exact sequence

$$ 0\to \textrm{Ker}\langle m\rangle\to \Delta_{w_{i,j}}\langle m\rangle\to L_{w_{i,j}}\langle m\rangle\to 0,$$

we get the exact sequence

\begin{multline*}0\to \textrm{hom}(L_{w_{i,j}}\langle m\rangle, \Delta_{w})\to\textrm{hom}(\Delta_{w_{i,j}}\langle m\rangle, \Delta_{w})\to\textrm{hom}(\textrm{Ker}\langle m\rangle, \Delta_{w})\\ \to\textrm{ext}^1(L_{w_{i,j}}\langle m\rangle, \Delta_{w})\to\textrm{ext}^1(\Delta_{w_{i,j}}\langle m\rangle, \Delta_{w}).\end{multline*}

Here $\textrm{hom}(L_{w_{i,j}}\langle m\rangle, \Delta_{w})=0$ since $w_{i,j}\neq w_0$ .

The above implies that the map

$$ \textrm{hom}(\Delta_{w_{i,j}}\langle m\rangle, \Delta_{w})\to\textrm{hom}(\textrm{Ker}\langle m\rangle, \Delta_{w})$$

is an inclusion. Under the assumption $w_{i,j}\geq w$ , this map, in fact, is an isomorphism. Indeed, we even have

$$ \mathbb{C}\cong\textrm{Hom}_{\mathcal{O}}(\Delta_{w_{i,j}}, \Delta_{w})\cong\textrm{Hom}_{\mathcal{O}}(\textrm{Ker}, \Delta_{w}).$$

Here the first isomorphism is a consequence of $w_{i,j}\geq w$ while the second one is given by the restriction together with the fact that the last hom-space is one-dimensional since both involved modules have isomorphic simple socle which, moreover, has multiplicity one in both modules.

This implies that the map

$$ \textrm{ext}^1(L_{w_{i,j}}\langle m\rangle, \Delta_{w})\to\textrm{ext}^1(\Delta_{w_{i,j}}\langle m\rangle, \Delta_{w})$$

is injective. Since $\textrm{ext}^1(L_{w_{i,j}}\langle m\rangle, \Delta_{w})\neq 0$ by [ 19 , corollary 2], the claim follows.

We note that the non-zero extension in $\textrm{ext}^1(\Delta_{w_{i,j}}\langle m\rangle,\Delta_{w})$ produced by Proposition 21 is expected if and only if $-m=\ell(w_{i,j})-\ell(w)-2$ . In all other cases, we have an additional extension.

Corollary 22. For $i\in\{1,2,\dots,n-1\}$ , consider the element $w_{i,n-i}=s_iw_0$ . Let $w\in S_n$ and let $m = 2- (\ell(w_{i,n-i})-\ell(w))$ (the expected degree of $ext^1$ between $\Delta_{w_{i,n-i}}$ and $\Delta_{w}$ ).

1. (a) If $\Phi_{i,n-i}^{-1} (L_{w_{i,n-i}}\langle m'\rangle )\not\in BM_w$ for all $m'\neq m$ , then we have

   \begin{equation*}\dim\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{i,n-i}},\Delta_{w})=\dim\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m\rangle,\Delta_{w})=|r^{({-}m)}_{w_{i,n-i},w}|.\end{equation*}

2. (b) If $\Phi_{i,n-i}^{-1} (L_{w_{i,n-i}}\langle m' \rangle )\in BM_w$ for some $m'\neq m$ , then we have

   $$ \textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{i,n-i}},\Delta_{w})=\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m'\rangle,\Delta_{w})\oplus\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m\rangle,\Delta_{w}).$$
   Moreover, we have $\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m'\rangle,\Delta_{w})\cong\mathbb{C}$ , while $\dim\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m\rangle,\Delta_{w})=|r^{({-}m)}_{w_{i,n-i},w}|$ .

Proof. Since $w_{i,n-i}=s_iw_0$ , we have the exact sequence

$$ 0\to \Delta_{w_0}\langle -1\rangle\to\Delta_{w_{i,n-i}}\to L_{w_{i,n-i}}\to 0.$$

It induces the exact sequence

$$ \textrm{Ext}^1_{\mathcal{O}}(L_{w_{i,n-i}}, \Delta_{w})\to\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{i,n-i}}, \Delta_{w})\to\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{0}}, \Delta_{w}).$$

By [ 21 , theorem 32], any element in $\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{0}}, \Delta_{w})$ is expected. By [ 19 , corollary 2], the dimension of $\textrm{Ext}^1_{\mathcal{O}}(L_{w_{i,n-i}}, \Delta_{w})$ is at most 1. This naturally splits our consideration into two cases, for the potential degree shift $\tilde{m}$ , namely, the cases $-{\tilde{m}}=\ell(w_{i,{n-i}}){-\ell(w)}-2$ and $-{\tilde{m}}\neq \ell(w_{i,{n-i}}){-\ell(w)}-2$ . In the first case, all first extensions are expected and thus given by (11). This is exactly claim (a).

Now, assume that $-{\tilde{m}}\neq \ell(w_{i,{n-i}}){-\ell(w)}-2$ . The proof of Proposition 21 constructs an embedding from $\textrm{ext}^1(L_{w_{i,n-i}}\langle {\tilde{m}}\rangle, \Delta_{w})$ to $\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle {\tilde{m}}\rangle, \Delta_{w})$ . We have the vanishing $\textrm{ext}^1(\Delta_{w_{0}}\langle {\tilde{m}}-1\rangle, \Delta_{w})=0$ by [ 21 , theorem 32]. This implies that the above embedding is, in fact, an isomorphism. Now claim (b) follows from [ 19 , corollary 2] and the observation that all expected extensions are given by (11).

Example 23. Consider $S_{2n}$ , for $n>2$ , and $w_{n,n}=s_nw_0$ . Let $w=s_n$ , which is bigrassmannian. Then the socle of the module $\Delta_e/\Delta_{s_n}$ is isomorphic to the module $L_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle$ . Hence $\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{i,j}},\Delta_{w})$ has the expected part of dimension $2n-1$ (corresponding to $\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-3)\rangle,\Delta_{s_2})$ ) and also the one-dimensional additional part $\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle,\Delta_{s_n})$ .

6·5. Some additional higher extensions

This section presents a few ways to find additional, in the sense of Subsection 4·5, higher extensions.

We start with the first type of examples observed (in an ungraded setting) by Boe [ 7 ] in disproving the Gabber–Joseph conjecture.

Example 24. If the coefficients $r_{x,y}^{(k)}$ do not alternate in sign, then Theorem 2 implies that there is an additional extension between $\Delta_x$ and $\Delta_y$ . (Here we cannot determine the i such that there are additional ith extensions.) Computer computation of $r_{x,y}$ provides many such examples. We record two here:

In type $D_4$ , the coefficients of $r_{e,w_0}$ are

\begin{equation*}[1, -4, 7, -8, 6, 0, -4, 0, 6, -8, 7, -4, 1].\end{equation*}

The coefficients of $r_{e,w_0}$ in type $E_7$ are

\begin{equation*}[\!-\!1, 7, -22, 42, -57, 63, -65, 71, -87, 113, -137, 127, -55, -47, 111, -137, 173,\end{equation*}

\begin{equation*}-171,23, 223, -399, 505, -708, 1052, -1396, 1580, -1530, 1302, -984, 456, 430,\end{equation*}

\begin{equation*}-1250, 1250,-430, -456, 984, -1302, 1530, -1580, 1396, -1052, 708, -505, 399,\end{equation*}

\begin{equation*}-223, -23, 171, -173,137, -111, 47, 55, -127, 137, -113, 87, -71,65, -63, 57,\end{equation*}

\begin{equation*} -42, 22, -7, 1].\end{equation*}

The second type of examples are also, more or less, combinatorial, this time depending on computations of KL polynomials rather than R-polynomials and using Proposition 5 rather than Theorem 2.

Example 25. Let W be of type $B_3$ with the labelling . We claim that:

1. (1) either $\textrm{Ext}^2(\Delta_{w_0},\Delta_e)$ or $\textrm{Ext}^2(\Delta_{w_0},\Delta_{s_0})$ contains additional extensions;

2. (2) either $\textrm{Ext}^3(\Delta_{w_0},\Delta_e)$ or $\textrm{Ext}^3(\Delta_{w_0},\Delta_{s_0})$ contains additional extensions;

3. (3) either $\textrm{Ext}^4(\Delta_{w_0},\Delta_e)$ or $\textrm{Ext}^4(\Delta_{w_0},\Delta_{s_0})$ contains additional extensions.

A computation of KL polynomials, together with Proposition 5, shows that the dimensions of $\hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{a}(\Delta_e)) $ and $\hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{a-1}(\Delta_{s_0}))$ are as in Figure 3. Recall that the embedding $\mathcal{T}_{\bullet-1}(\Delta_{s_0})\to \mathcal{T}_{\bullet}(\Delta_{e})$ induces an embedding

\begin{equation*}\iota:\hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{\bullet-1}(\Delta_{s_0}))\to \hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{\bullet}(\Delta_e)).\end{equation*}

The claims additional extensions arise from the square (i.e., additional) coordinates (a,b) where the dimension difference at $(a-1,b)$ is greater than the difference at (a,b) in Figure 3. We explain the details for the details for (1). The same argument applies to the other claims.

Figure 3. $\dim \hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_a(\Delta_e)) $ versus $\dim \hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{a-1}(\Delta_{s_0})) $

Suppose the second extension between $\Delta_{w_0}$ and $\Delta_e$ is expected. Then the map

\begin{equation*}d\circ - :\hom(\Delta_{w_0}\langle -1\rangle,\mathcal{T}_{2}(\Delta_e)) \to \hom(\Delta_{w_0}\langle -1\rangle,\mathcal{T}_{3}(\Delta_e))\end{equation*}

is injective, where d is the (relevant restriction of) differential of $\mathcal{T}_\bullet(\Delta_e)$ . Let V be its 3-dimensional image in $\hom(\Delta_{w_0}\langle -1\rangle,\mathcal{T}_{3}(\Delta_e))$ . The embedding $\iota$ restricts to an isomorphism

\begin{equation*}\iota:\hom(\Delta_{w_0}\langle -1\rangle,\mathcal{T}_{3-1}(\Delta_{s_0}))\xrightarrow[]{\simeq} \hom(\Delta_{w_0}\langle -1\rangle,\mathcal{T}_{3}(\Delta_e)),\end{equation*}

also denoted by $\iota$ , since both spaces are of dimension 7. We obtain a 3-dimensional subspace $\iota^{-1}(V)$ in the 7-dimensional space $\hom(\Delta_{w_0}\langle -1\rangle,\mathcal{T}_{3-1}(\Delta_{s_0}))$ which corresponds to morphisms of complexes from $\Delta_{w_0}\langle-1\rangle$ to $\mathcal{T}_\bullet(\Delta_{s_0})$ . At most (in fact exactly) two dimensional subspace of $\iota^{-1}$ is homotopic to zero, because the dimension of at $(2,-1)$ is two. Thus the rest contributes to a nonzero element in $\textrm{ext}^2(\Delta_{w_0}\langle-1\rangle,\Delta_{s_0})$ which is additional.

Another way to construct additional extensions is to use [ 19 ] and Subsection 6·4, as in the following proposition.

Proposition 26. In the setup of Example 23, the Yoneda product of an additional element in $\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle,\Delta_{s_n})$ and an additional element in $\textrm{ext}^1(\Delta_{s_n}\langle 1\rangle,\Delta_e)$ gives an additional element in

$$ \textrm{ext}^2(\Delta_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle,\Delta_{e}).$$

This implies that $\textrm{ext}^2(\Delta_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle,\Delta_{e})\neq 0$ and gives an example of an additional second extension.

Proof. From the Koszul–Ringel self-duality, it follows that the complex $\mathcal{T}_\bullet(\Delta_{s_n})[\!-\!1]\langle 1\rangle$ is a subcomplex of the complex $\mathcal{T}_\bullet(\Delta_e)$ . This inclusion corresponds precisely to an additional element in $\textrm{ext}^1(\Delta_{s_n}\langle 1\rangle,\Delta_e)$ .

A non-zero element in $\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle,\Delta_{s_n})$ corresponds to a non-zero homomorphism in the homotopy category of complexes from the singleton complex $\Delta_{w_{n,n}}[\!-\!1]\langle -(n(2n-1)-1-2(n-1))\rangle$ to $\mathcal{T}_\bullet(\Delta_{s_n})$ . Therefore, to prove the claim it is enough to show that the map from $\Delta_{w_{n,n}}[\!-\!2]\langle -(n(2n-1)-2(n-1))\rangle$ to $\mathcal{T}_\bullet(\Delta_e)$ induced by the inclusion of $\mathcal{T}_\bullet(\Delta_{s_n})[\!-\!1]\langle 1\rangle$ to $\mathcal{T}_\bullet(\Delta_e)$ is not homotopic to zero.

To prove this, it is enough to show that there are no non-zero homomorphisms from $\Delta_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle$ to any indecomposable direct summand of $\mathcal{T}_1(\Delta_e)$ outside of $\mathcal{T}_0(\Delta_{s_n})[\!-\!1]\langle 1\rangle$ .

These direct summands are exactly the modules $T_{s_i}\langle 1\rangle$ , where $i\neq n$ . Since $T_{s_i}$ is a tilting module, a non-zero homomorphism from $\Delta_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle$ to $T_{s_i}\langle 1\rangle$ exists if and only if $\nabla_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle$ is a subquotient of a dual Verma flag of $T_{s_i}\langle 1\rangle$ . Using $\top_{w_0}$ , this is equivalent to $\Delta_{s_n}\langle -(n(2n-1)-2(n-1))\rangle$ being a subquotient of a dual Verma flag of $P_{w_0s_i}\langle 1\rangle$ . By the BGG reciprocity, this is equivalent to $L_{w_0s_i}\langle -(n(2n-1)-2(n-1))\rangle$ being a composition subquotient of $\Delta_{s_n}$ .

Note that $w_0s_i$ belongs to the penultimate KL-cell in the terminology of [ 19 ]. All graded simple penultimate subquotients of $\Delta_e$ are described in [ 19 , proposition 12]. From [ 19 , theorem 1] it follows that the socle of the module $\Delta_e/(\Delta_{s_n}\langle -1\rangle)$ is the unique penultimate subquotient of of this module and that it occurs in the minimal possible degree (in $\Delta_e$ ) among all other penultimate subquotients of $\Delta_e$ . It follows that any other simple subquotient of $\Delta_{s_n}$ of the form $L_{w_0s_i}$ appears in $\Delta_e$ in a strictly higher degree compared to the degree of the socle of $\Delta_e/(\Delta_{s_n}\langle -1\rangle)$ . Going back via the BGG reciprocity and the Ringel duality, we get exactly the claim that any subquotient $\nabla_{w_{n,n}}\langle d\rangle$ of a dual Verma flag of $T_{s_i}\langle 1\rangle$ must be shifted strictly more than by $-(n(2n-1)-2(n-1))$ . This completes the proof.

7. Extensions between singular and between parabolic Verma modules

We briefly discuss generalisations of the previous sections to singular and parabolic categories $\mathcal O$ .

7·1. Singular blocks of $\mathcal{O}$

Thanks to Soergel’s combinatorial description of blocks of category $\mathcal{O}$ , see [ 28 ], it is known that every block of $\mathcal{O}$ is equivalent to an integral (but, in general, singular) block of $\mathcal{O}$ (however, possibly, for a different Lie algebra). Therefore the complete version of the problem to describe extensions between Verma modules must address the case of singular integral blocks.

Let $\mathfrak{p}$ denote a parabolic subalgebra of $\mathfrak{g}$ containing the Borel subalgebra $\mathfrak{h}\oplus\mathfrak{n}_+$ . The subalgebra $\mathfrak{p}$ is uniquely determined by a subset of simple roots, or, equivalently, by the corresponding parabolic subgroup $W^{\mathfrak{p}}$ of W. Let $\textbf{R}^\mathfrak{p}_{\textrm{short}}$ denote the set of the shortest coset representatives in $W/W^{\mathfrak{p}}$ .

Let $\lambda$ be a dominant integral weight such that $W^{\mathfrak{p}}$ is exactly the dot-stabilizer of $\lambda$ . Consider the block $\mathcal{O}_\lambda$ of $\mathcal{O}$ containing $L(\lambda)$ . Then the simple objects in $\mathcal{O}_\lambda$ are $\{L(w\cdot\lambda)\,:\, w\in\textbf{R}^\mathfrak{p}_{\textrm{short}}\}$ . Similarly to the regular case, we also have the corresponding projective, injective, Verma, dual Verma and tilting modules and their graded versions.

7·2. Regular blocks of parabolic category $\mathcal{O}$

Associated to our choice of $\mathfrak{p}$ , one also has the parabolic category $\mathcal{O}^\mathfrak{p}$ introduced in [ 27 ]. It is defined as the full subcategory of $\mathcal{O}$ consisting of all objects, the action of $U(\mathfrak{p})$ on which is locally finite.

Let $\textbf{L}^\mathfrak{p}_{\textrm{short}}$ denote the set of the shortest coset representatives in $W^{\mathfrak{p}}\backslash W$ . Then the category $\mathcal{O}_0^\mathfrak{p}$ is the Serre subcategory of $\mathcal{O}_0$ generated by all $L_w$ such that $w\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ . We use the superscript $\mathfrak{p}$ to denote structural objects in $\mathcal{O}_0^\mathfrak{p}$ . In particular, for $w\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ , we denote by $P^\mathfrak{p}_w$ the indecomposable projective cover of $L^\mathfrak{p}_w=L_w$ in $\mathcal{O}_0^\mathfrak{p}$ and so on. The category $\mathcal{O}_0^\mathfrak{p}$ inherits a graded lift from that for $\mathcal{O}_0$ .

7·3. Koszul–Ringel duality

For a fixed parabolic subalgebra $\mathfrak{p}$ as above and singular dominant integral $\lambda$ with dot-stabilizer $W^\mathfrak{p}$ , the combination of Koszul and Ringel dualities, together with the autoequivalence given by the conjugation with $w_0$ , see [ 3, 22, 29 ], gives rise to the equivalence

$$ \mathcal{D}^b\big((\mathcal{O}_\lambda)^\mathbb{Z}\big)\cong\mathcal{D}^b\big((\mathcal{O}_0^\mathfrak{p})^\mathbb{Z}\big)$$

which sends $\Delta(w\cdot \lambda)$ to $\Delta^{\mathfrak{p}}_{w^{-1}}$ , where $w\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$ .

In particular, this implies that

$$ \textrm{ext}^k(\Delta(x\cdot \lambda),\Delta(y\cdot\lambda)\langle j\rangle)\cong\textrm{ext}^{k+j}(\Delta^\mathfrak{p}_{x^{-1}},\Delta^\mathfrak{p}_{y^{-1}}\langle -j\rangle)$$

and thus the problem to determine all extensions between singular Verma modules is equivalent to the problem to detrmine all extensions between regular parabolic Verma modules.

7·4. Singular and parabolic R-polynomials

Consider the usual $\mathbb{Z}[v,v^{-1}]$ -structure on the Grothendieck group $\textrm{Gr}(\mathcal{O}_\lambda^{\mathbb{Z}})$ . Similarly to the regular case, the group $\textrm{Gr}(\mathcal{O}_\lambda^{\mathbb{Z}})$ has various bases given by the classes of simple, standard, costandard, projective, injective and tilting objects.

The singular R-polynomials $\{sr_{x,y}\,:\,x,y\in W\}$ are defined as the entries of the transformation matrix between the standard and the costandard bases in $\textrm{Gr}(\mathcal{O}_\lambda^{\mathbb{Z}})$ , i.e.:

$$ [\Delta(y\cdot \lambda)]=\sum_{x\in\textbf{R}^\mathfrak{p}_{\textrm{short}}}sr_{x,y}[\nabla(x\cdot\lambda)],\text{ for all } y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}.$$

Note that $sr_{x,y}\in\mathbb{Z}[v,v^{-1}]$ , by definition. For $x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$ and $k\in\mathbb{Z}$ , we denote by $sr_{x,y}^{(k)}$ the coefficient at $v^k$ in $sr_{x,y}$ .

Let $w_0^\mathfrak{p}$ denotes the longest element in $W^\mathfrak{p}$ . The connection between the usual and the singular R-polynomials is clarified by the following:

Lemma 27. For $x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$ , we have

$$ sr_{x,y}=\sum_{w\in W^\mathfrak{p}}r_{x,yw}v^{\ell(w)-2\ell(w_0^\mathfrak{p})}.$$

Proof. Let $\theta_{\lambda}^{\textrm{on}}$ be the translation functor to the $\lambda$ -wall, that is the unique indecomposable projective functor in the sense of [ 5 ] which sends $\Delta_e$ to $\Delta_{\lambda}$ . Then $\theta_{\lambda}^{\textrm{on}}$ sends $\Delta_y$ to $\Delta(y\cdot \lambda)$ . Furthermore, for $y\in \textbf{R}^\mathfrak{p}_{\textrm{long}}$ and $w\in W^\mathfrak{p}$ , we have

$$ \theta_{\lambda}^{\textrm{on}}\nabla_{yw}\cong\nabla(y\cdot\lambda)\langle 2\ell(w_0^\mathfrak{p})-\ell(w)\rangle.$$

Since $\theta_{\lambda}^{\textrm{on}}$ is exact, the claim now follows from the definitions.

Consider the usual $\mathbb{Z}[v,v^{-1}]$ -structure on the Grothendieck group $\textrm{Gr}\big((\mathcal{O}_0^\mathfrak{p})^{\mathbb{Z}}\big)$ . Similarly to the regular case, the group $\textrm{Gr}\big((\mathcal{O}_0^\mathfrak{p})^{\mathbb{Z}}\big)$ has various bases given by the classes of simple, standard, costandard, projective, injective and tilting objects.

The parabolic R-polynomials $\{pr_{x,y}\,:\,x,y\in W\}$ are defined as the entries of the transformation matrix between the standard and the costandard bases in $\textrm{Gr}\big((\mathcal{O}_0^\mathfrak{p})^{\mathbb{Z}}\big)$ , i.e.:

$$ [\Delta_y^\mathfrak{p}]=\sum_{x\in\textbf{L}^\mathfrak{p}_{\textrm{short}}}pr_{x,y}[\nabla_x^\mathfrak{p}],\text{ for all } y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}.$$

Note that $pr_{x,y}\in\mathbb{Z}[v,v^{-1}]$ , by definition. For $x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ and $k\in\mathbb{Z}$ , we denote by $pr_{x,y}^{(k)}$ the coefficient at $v^k$ in $pr_{x,y}$ .

As $\Delta_{w_0^\mathfrak{p}w_0}^\mathfrak{p}=\nabla_{w_0^\mathfrak{p}w_0}^\mathfrak{p}$ , we have

(13) \begin{equation}pr_{x,w_0^\mathfrak{p}w_0}=\begin{cases}1,& x=w_0^\mathfrak{p}w_0;\\0,& \text{otherwise}.\end{cases}\end{equation}

For $w\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ and $s\in S$ such that $ws\not\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ , we have $\theta_s\Delta^\mathfrak{p}_w=\theta_s\nabla^\mathfrak{p}_w=0$ . If $ws\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ and $ws>w$ , then we have

$$ [\theta_s\Delta^\mathfrak{p}_w]=v[\theta_s\Delta^\mathfrak{p}_{ws}]=[\Delta^\mathfrak{p}_{ws}]+v[\Delta^\mathfrak{p}_w]\,\text{ and }\,[\theta_s\nabla^\mathfrak{p}_w]=v^{-1}[\theta_s\nabla^\mathfrak{p}_{ws}]=[{\nabla_{ws}^\mathfrak{p}}]+v^{-1}[\nabla^\mathfrak{p}_w].$$

From this, we have the following recursive formula for parabolic R-polynomials: For $x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ and $s\in S$ such that $ys<y$ and $ys\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ , we have:

(14) \begin{equation}pr_{x,ys}=\begin{cases}pr_{xs,y},& xs<x\text{ and }xs\in \textbf{L}^\mathfrak{p}_{\textrm{short}};\\pr_{xs,y}+ ({v-v^{-1}}){pr_{x,y}},& xs>x\text{ and }xs\in \textbf{L}^\mathfrak{p}_{\textrm{short}};\\-v\, pr_{x,y},& xs\not\in \textbf{L}^\mathfrak{p}_{\textrm{short}}.\end{cases}\end{equation}

Together, (13) and (14) determine the family of parabolic R-polynomials uniquely.

Koszul–Ringel duality relates these two families of polynomials as follows:

Proposition 28. For all $x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ , we have $pr_{x,y}(v)=sr_{x^{-1},y^{-1}}(-v^{-1})$ .

Proof. Taking into account that the conjugation by $w_0$ is an automorphism of the Dynkin diagram, the claim of the proposition follows from the definitions using that the Koszul–Ringel duality sends $\Delta(w\cdot\lambda)$ to $\Delta^\mathfrak{p}_{w_0w^{-1}w_0}$ and $\nabla(w\cdot \lambda)$ to $\nabla_{w_0w^{-1}w_0}^\mathfrak{p}$ and intertwines $[i]\langle j\rangle$ with $[i+j]\langle -j\rangle$ .

7·5. Delorme formulae

Similarly to the regular case, we have both ungraded and graded versions of Delorme formulae for both, the singular and the parabolic cases, with the same proofs as for the regular case.

Proposition 29.

1. (a) For $x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$ , we have

   $$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{Ext}^i_{\mathcal{O}}(\Delta(x\cdot\lambda),\Delta(y\cdot\lambda))=\delta_{x,y}.$$

2. (b) For $x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ , we have

   $$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{Ext}^i_{\mathcal{O}^\mathfrak{p}}(\Delta_x^\mathfrak{p},\Delta_y^\mathfrak{p})=\delta_{x,y}.$$

Proposition 30.

1. (a) For $x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$ and $k\in\mathbb{Z}$ , we have

   $$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{ext}^i(\Delta(x\cdot\lambda)\langle -k\rangle,\Delta(y\cdot\lambda))=sr_{x,y}^{(k)}.$$

2. (b) For $x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$ and $k\in\mathbb{Z}$ , we have

   $$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{ext}^i_{(\mathcal{O}^\mathfrak{p})^\mathbb{Z}}(\Delta_x^\mathfrak{p}\langle -k\rangle,\Delta_y^\mathfrak{p})=pr_{x,y}^{(k)}.$$

7·6. Expected and additional extensions

Under the indexing conventions in Subsections 7·1, 7·2, the expected extensions between singular or parabolic Verma modules are the extensions in

\begin{equation*}\textrm{ext}^k(\Delta(x\cdot \lambda),\Delta(y\cdot\lambda)\langle j\rangle),\quad\textrm{ext}^{k+j}(\Delta^\mathfrak{p}_{x},\Delta^\mathfrak{p}_{y}\langle -j\rangle)\end{equation*}

where $2k+j = \ell(x)-\ell(y)$ . The other (nonzero) extensions are additional. If all extensions are expected, then Proposition 30 says that the dimensions of the expected ext spaces are given by the R-polynomials.

7·7. Koszulity

Consider the categoy $\mathcal{D}^b(\mathcal{O}_\lambda^\mathbb{Z})$ , for a dominant and integral (but not necessarily regular) $\lambda$ . Denote by $\mathscr{D}$ the full subcategory of $\mathcal{D}(\mathcal{O}_\lambda^\mathbb{Z})$ given by the objects $\Delta(w\cdot\lambda)\langle i\rangle[j]$ , where $w\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$ and $i,j\in\mathbb{Z}$ such that

$$ i\in\{-\ell(w)-2j,-\ell(w)-2j-1\}.$$

Then the same argument as Theorem 17 gives the following generalisation.

Theorem 31. Let $\lambda$ be dominant and integral. Assume that all extensions between the Verma modules in $\mathcal{O}_\lambda$ are expected. Then the following assertions hold:

1. (i) We have an equivalence $\mathcal{D}^*(\mathcal{O}_\lambda^\mathbb{Z})\cong \mathcal{D}^*(\mathscr{D}\text{-}\textrm{mod})$ where $*\in\{b,\uparrow,\downarrow\}$ .

2. (ii) The path algebra of $\mathscr{D}$ is Koszul and is Koszul self-dual.