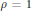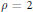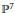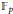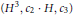6 results
Linear PDE with constant coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. S2-S27
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SMOOTH FANO 4-FOLDS IN GORENSTEIN FORMATS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 31 May 2021, pp. 424-433
- Print publication:
- December 2021
-
- Article
- Export citation
Variation of Mixed Hodge Structures Associated to an Equisingular One-dimensional Family of Calabi-Yau Threefolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 16 January 2020, pp. 441-464
- Print publication:
- April 2021
-
- Article
- Export citation
VARIETIES OF SIGNATURE TENSORS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 04 April 2019, e10
-
- Article
-
- You have access
- Open access
- Export citation
Divisorial Models of Normal Varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 1053-1064
-
- Article
- Export citation
Examples of Calabi–Yau 3-Folds of ℙ7 with ρ = 1
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 5 / 01 October 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1050-1072
- Print publication:
- 01 October 2009
-
- Article
-
- You have access
- Export citation

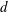
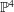
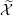
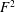
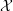
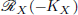 is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.
is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.