Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-18T13:21:07.530Z Has data issue: false hasContentIssue false
  • English
  • Français

Examples of Calabi–Yau 3-Folds of ℙ7 with ρ = 1

Published online by Cambridge University Press:  20 November 2018

Marie-Amélie Bertin
Marie-Amélie Bertin*
Affiliation:
12 rue des Bretons, 94700 Maisons Alfort, France, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

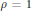We give some examples of Calabi–Yau 3-folds with $\rho =1$ and 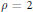$\rho =2$, defined over 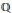$\mathbb{Q}$ and constructed as 4-codimensional subvarieties of 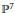${{\mathbb{P}}^{7}}$ via commutative algebra methods. We explain how to deduce their Hodge diamond and top Chern classes from computer based computations over some finite field 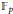${{\mathbb{F}}_{p}}$. Three of our examples (of degree 17 and 20) are new. The two others (degree 15 and 18) are known, and we recover their well-known invariants with our method. These examples are built out of Gulliksen–Negård and Kustin–Miller complexes of locally free sheaves.

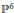Finally, we give two new examples of Calabi–Yau 3-folds of ${{\mathbb{P}}^{6}}$ of degree 14 and 15 (defined over 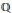$\mathbb{Q}$). We show that they are not deformation equivalent to Tonoli's examples of the same degree, despite the fact that they have the same invariants 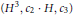$({{H}^{3}},{{c}_{2}}\cdot H,{{c}_{3}})$ and 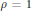$\rho =1$.

Keywords

14J3214Q15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 5 , 01 October 2009 , pp. 1050 - 1072
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Buchsbaum, D. and Eisenbud, D., Algebra structure for finite free resolutions, and some structure theorem for Gorenstein ideals of codimension 3. Amer J. Math. 99(1977), no. 3, 447–485.Google Scholar
[2] Gulliksen, T. and Neg°ard, O., Un complexe résolvant pour certains idéaux déterminentiels. C. R. Acad. Sci. Sér. A-B 274(1972), A16–A18.Google Scholar
[3] Decker, W., Ein, L., and Schreyer, F.-O., Construction of surfaces in P4. J. Algebraic Geom. 2(1993), no. 2, 185–237.Google Scholar
[4] Kustin, A. and Miller, M., Structure theory for a class of grade four Gorenstein ideals. Trans. Amer. Math. Soc. 270(1982), no. 1, 287–307.Google Scholar
[5] Kustin, A. and Miller, M., Constructing big Gorenstein ideals from small ones. J. Algebra 85(1983), no. 2, 303–322.Google Scholar
[6] Lascoux, A., Syzygies des variétés déterminantales , Adv. in Math. 30(1978), no. 3, 202–237.Google Scholar
[7] Lee, N.-H., Calabi–Yau coverings over some singular varieties and new Calabi–Yau 3-folds with Picard number one. Manuscripta Math. 125(2008), no. 4, 531–547.Google Scholar
[8] Lee, N.-H., Calabi–Yau construction by smoothing normal crossing varieties. arXiv:math.AG/0604596.Google Scholar
[9] Mumford, D., Abelian Varieties. Oxford University Press, 1970.Google Scholar
[10] Okonek, C., Note on varieties of codimension 3 in PN. Manuscripta Math. 84(1994), no. 3-4, 421–442.Google Scholar
[11] Papadakis, S., Kustin– Miller unprojection with complexes. J. Algebraic Geom. 13(2004), no. 2, 249–266.Google Scholar
[12] Pragacz, P. and Weyman, J., Complexes associated with trace and evaluation. Another appraoch to Lascoux's resolution. Adv. in Math. 57(1985) no. 2, 163–207.Google Scholar
[13] Tonoli, F., Construction of Calabi–Yau 3-folds in P6. J. Algebraic Geom. 13(2004), no. 2, 209–232.Google Scholar
[14] van Enckevort, C. and van Straten, D., Monodromy calculations of fourth order equations of Calabi–Yau type. In: Mirror Symmetry. A MS/IP Stud. Adv. Math. 38, American Mathematical Society, Providence, RI, 2006, pp. 539–559.Google Scholar