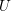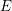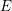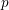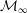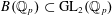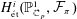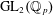8 results
Families of Picard modular forms and an application to the Bloch–Kato conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1327-1401
- Print publication:
- July 2019
-
- Article
- Export citation
A QUOTIENT OF THE LUBIN–TATE TOWER
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 27 July 2017, e17
-
- Article
-
- You have access
- Open access
- Export citation
Strict supports of canonical measures and applications to the geometric Bogomolov conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 997-1040
- Print publication:
- May 2016
-
- Article
- Export citation
Coleman integration for even-degree models of hyperelliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 258-265
-
- Article
-
- You have access
- Export citation
Slopes of the U7 operator acting on a space of overconvergent modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 113-139
-
- Article
-
- You have access
- Export citation
Non-archimedean canonical measures on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 21 April 2010, pp. 683-730
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
Local solutions to positive characteristic non-Archimedean differential equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1465-1477
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
On $\ell$-independence for the étale cohomology of rigid spaces over local fields
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 2 / March 2007
- Published online by Cambridge University Press:
- 26 March 2007, pp. 393-422
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation