Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-13T16:54:57.278Z Has data issue: false hasContentIssue false
  • English
  • Français

Families of Picard modular forms and an application to the Bloch–Kato conjecture

Part of: Algebraic groups Arithmetic algebraic geometry Abelian varieties and schemes Discontinuous groups and automorphic forms Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  25 June 2019

Valentin Hernandez
Valentin Hernandez*
Affiliation:
Département de Mathématiques, Faculté des Sciences d’Orsay, Université Paris-Sud, Bâtiment 307, 91405 Orsay, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we construct a p-adic three-dimensional eigenvariety for the group 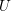$U$(2,1)(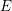$E$), where 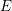$E$ is a quadratic imaginary field and 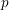$p$ is inert in 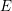$E$. The eigenvariety parametrizes Hecke eigensystems on the space of overconvergent, locally analytic, cuspidal Picard modular forms of finite slope. The method generalized the one developed in Andreatta, Iovita and Stevens [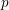$p$-adic families of Siegel modular cuspforms Ann. of Math. (2) 181, (2015), 623–697] by interpolating the coherent automorphic sheaves when the ordinary locus is empty. As an application of this construction, we reprove a particular case of the Bloch–Kato conjecture for some Galois characters of 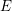$E$, extending the results of Bellaiche and Chenevier to the case of a positive sign.

Keywords

eigenvarietiesp-adic automorphic formsPicard modular varietiesBloch–Kato conjecturep-divisible groups

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties 11F33: Congruences for modular and $p$-adic modular forms 14K10: Algebraic moduli, classification
Secondary: 11F55: Other groups and their modular and automorphic forms (several variables) 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture 14L05: Formal groups, $p$-divisible groups 14G35: Modular and Shimura varieties 14G22: Rigid analytic geometry
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 7 , July 2019 , pp. 1327 - 1401
Copyright
© The Author 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreatta, F., Bijakowski, S., Iovita, A., Kassaei, P. L., Pilloni, V., Stroh, B., Tian, Y. and Xiao, L., Arithmétique p-adique des formes de Hilbert (Société Mathématique de France, Paris, 2016).Google Scholar
Andreatta, F., Iovita, A. and Pilloni, V., p-adic families of Siegel modular cuspforms , Ann. of Math. (2) 181 (2015), 623–697.10.4007/annals.2015.181.2.5Google Scholar
Andreatta, F., Iovita, A. and Stevens, G., Overconvergent modular sheaves and modular forms for GL2/F , Israel J. Math. 201 (2014), 299–359.10.1007/s11856-014-1045-8Google Scholar
Ash, A. and Stevens, G., $p$ -Adic deformations of arithmetic cohomology, Preprint (2008),https://www2.bc.edu/avner-ash/Papers/Ash-Stevens-Oct-07-DRAFT-copy.pdf.Google Scholar
Barnet-Lamb, T., Geraghty, D., Harris, M. and Taylor, R., A family of Calabi-Yau varieties and potential automorphy. II , Publ. Res. Inst. Math. Sci. 47 (2011), 29–98.10.2977/PRIMS/31Google Scholar
Bellaïche, J., Congruences endoscopiques et représentations galoisiennes, Thèse de doctorat, Université de Paris-Sud, Faculté des Sciences d’Orsay (Essonne) (2002).Google Scholar
Bellaïche, J., A propos d’un lemme de Ribet , Rend. Semin. Mat. Univ. Padova 109 (2003), 45–62.Google Scholar
Bellaïche, J., Sur la compatibilité entre les correspondances de Langlands locale et globale pour U(3) , Comment. Math. Helv. 81 (2006), 449–470.10.4171/CMH/58Google Scholar
Bellaïche, J., Relèvement des formes modulaires de Picard , J. Lond. Math. Soc. (2) 74 (2006), 13–25.10.1112/S0024610706022824Google Scholar
Bellaïche, J., Ranks of selmer groups in an analytic family , Trans. Amer. Math. Soc. 364 (2012), 4735–4761.10.1090/S0002-9947-2012-05504-8Google Scholar
Bellaïche, J. and Chenevier, G., Formes non tempérées pour U (3) et conjectures de Bloch-Kato , Ann. Sci. Éc. Norm. Supér. (4) 37 (2004), 611–662.10.1016/j.ansens.2004.05.001Google Scholar
Bellaïche, J. and Chenevier, G., Families of Galois representations and Selmer groups (Société Mathématique de France, Paris, 2009).Google Scholar
Berthelot, P., Cohomologie rigide et cohomologie rigide à supports propres (Université de Rennes 1, Institut de Recherche Mathématique de Rennes [IRMAR], 1996).Google Scholar
Bijakowski, S., Analytic continuation on Shimura varieties with 𝜇-ordinary locus , Algebra Number Theory 10 (2016), 843–885.10.2140/ant.2016.10.843Google Scholar
Bijakowski, S., Formes modulaires surconvergentes, ramification et classicité , Ann. Inst. Fourier (Grenoble) 67 (2017), 2463–2518.10.5802/aif.3140Google Scholar
Bijakowski, S., Pilloni, V. and Stroh, B., Classicité de formes modulaires surconvergentes , Ann. of Math. (2) 183 (2016), 975–1014.10.4007/annals.2016.183.3.5Google Scholar
Blasco, L., Description du dual admissible de U (2, 1)(F) par la théorie des types de C. Bushnell et P. Kutzko , Manuscripta Math. 107 (2002), 151–186.10.1007/s002290100231Google Scholar
Blasius, D. and Rogawski, J. D., Tate classes and arithmetic quotients of the two-ball , in The zeta functions of Picard modular surfaces (Centre de Recherches Mathématiques, Université de Montréal, Montréal, QC, 1992), 421–444.Google Scholar
Bloch, S. and Kato, K., L-functions and Tamagawa numbers of motives , in The Grothendieck Festschrift, Vol. I, Progress in Mathematics, vol. 86 (Birkhäuser, Boston, MA, 1990), 333–400.Google Scholar
Brasca, R., Eigenvarieties for cuspforms over PEL type Shimura varieties with dense ordinary locus , Canad. J. Math. 68 (2016), 1227–1256.10.4153/CJM-2015-052-2Google Scholar
Buzzard, K., Eigenvarieties , in L-functions and Galois representations, London Mathematical Society Lecture Note Series, vol. 320 (Cambridge University Press, Cambridge, 2007), 59–120.10.1017/CBO9780511721267.004Google Scholar
Casselman, B., Introduction to admissible representations of p-adic groups, Preprint (1995),https://www.math.ubc.ca/ cass/research/pdf/p-adic-book.pdf.Google Scholar
Chenevier, G., Familles p-adiques de formes automorphes et applications aux conjectures de Bloch-Kato, Thèse de doctorat, Université Paris-Diderot, Paris 7 (2003).10.1515/crll.2004.031Google Scholar
Chenevier, G., Familles p-adiques de formes automorphes pour GLn , J. Reine Angew. Math. 570 (2004), 143–217.Google Scholar
Chenevier, G., Une correspondance de Jacquet-Langlands p-adique , Duke Math. J. 126 (2005), 161–194.10.1215/S0012-7094-04-12615-6Google Scholar
Chenevier, G. and Harris, M., Construction of automorphic Galois representations. II , Camb. J. Math. 1 (2013), 53–73.10.4310/CJM.2013.v1.n1.a2Google Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations , Publ. Math., Inst. Hautes Étud. Sci. 108 (2008), 1–181; with Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras.10.1007/s10240-008-0016-1Google Scholar
de Shalit, E. and Goren, E. Z., A theta operator on Picard modular forms modulo an inert prime , Res. Math. Sci. 3 (2016), Paper No. 28.10.1186/s40687-016-0075-8Google Scholar
Faltings, G., On the cohomology of locally symmetric Hermitian spaces , in Sémin. d’Algèbre Paul Dubreil et Marie-Paule Malliavin (Paris, 1982), Lecture Notes in Mathematics, vol. 1029 (Springer, Berlin, 1983), 55–98.10.1007/BFb0098927Google Scholar
Fargues, L., La filtration de Harder-Narasimhan des schémas en groupes finis et plats , J. Reine Angew. Math. 645 (2010), 1–39.10.1515/crelle.2010.058Google Scholar
Fargues, L., La filtration canonique des points de torsion des groupes p-divisibles , Ann. Sci. Éc. Norm. Supér. (4) 44 (2011), 905–961.10.24033/asens.2157Google Scholar
Fontaine, J.-M. and Perrin-Riou, B., Autour des conjectures de Bloch et Kato: Cohomologie galoisienne et valeurs de fonctions L , in Motives, Proc. summer research conf. on motives, Seattle, WA, 20 July–2 August 1991 (American Mathematical Society, Providence, RI, 1994), 599–706.Google Scholar
Goldring, W., Galois representations associated to holomorphic limits of discrete series , Compos. Math. 150 (2014), 191–228.10.1112/S0010437X13007355Google Scholar
Goldring, W. and Nicole, M.-H., The 𝜇-ordinary Hasse invariant of unitary Shimura varieties , J. Reine Angew. Math. 728 (2017), 137–151.Google Scholar
Gordon, B. B., Canonical models of Picard modular surfaces , in The zeta functions of Picard modular surfaces (Centre de Recherches Mathématiques, Université de Montréal, Montréal, QC, 1992), 1–29.Google Scholar
Harris, M., Arithmetic vector bundles of Shimura varieties , in Automorphic forms of several variables (Katata, 1983), Progress in Mathematics, vol. 46 (Birkhäuser, Boston, MA, 1984), 138–159.Google Scholar
Harris, M., Automorphic forms and the cohomology of vector bundles on Shimura varieties , in Automorphic forms, Shimura varieties, and L-functions, Proc. Conf., Ann Arbor MI, 1988, Vol. II, Perspectives in Mathematics, vol. 11 (Academic Press, Boston, MA, 1990), 41–91.Google Scholar
Harris, M., Automorphic forms of ∂̄-cohomology type as coherent cohomology classes , J. Differ. Geom. 32 (1990), 1–63.10.4310/jdg/1214445036Google Scholar
Hernandez, V., Invariants de hasse 𝜇-ordinaires , Ann. Inst. Fourier (Grenoble) 68 (2018), 1519–1607.10.5802/aif.3193Google Scholar
Hernandez, V., La filtration canonique des 𝓞-modules p-divisibles , Math. Ann. (2019), doi:10.1007/s00208-018-1789-2.Google Scholar
Hida, H., Iwasawa modules attached to congruences of cusp forms , Ann. Sci. Éc. Norm. Supér. (4) 19 (1986), 231–273.10.24033/asens.1507Google Scholar
Hsieh, M.-L., Eisenstein congruence on unitary groups and Iwasawa main conjectures for CM fields , J. Amer. Math. Soc. 27 (2014), 753–862.10.1090/S0894-0347-2014-00786-4Google Scholar
Jones, O. T. R., An analogue of the BGG resolution for locally analytic principal series , J. Number Theory 131 (2011), 1616–1640.10.1016/j.jnt.2011.02.010Google Scholar
Keys, D., Principal series representations of special unitary groups over local fields , Compos. Math. 51 (1984), 115–130.Google Scholar
Knapp, A. W., Representation theory of semisimple groups: an overview based on examples (PMS-36) (Princeton University Press, 2016).Google Scholar
Kottwitz, R. E., Points on some Shimura varieties over finite fields , J. Amer Math. Soc. 5 (1992), 373–444.10.1090/S0894-0347-1992-1124982-1Google Scholar
Lan, K.-W., Geometric modular forms and the cohomology of torsion automorphic sheaves , in Fifth international congress of Chinese mathematicians, Proc. ICCM ’10, Beijing, 17–22 December 2010, part 1 (American Mathematical Society, Providence, RI / International Press, Somerville, MA, 2012), 183–208.Google Scholar
Lan, K.-W., Arithmetic compactifications of PEL-type Shimura varieties, London Mathematical Society Monographs Series, vol. 36 (Princeton University Press, Princeton, NJ, 2013).Google Scholar
Lan, K.-W., Integral models of toroidal compactifications with projective cone decompositions , Int. Math. Res. Not. IMRN 2017 (2017), 3237–3280.Google Scholar
Langlands, R. P. and Ramakrishnan, D. (eds), The zeta functions of Picard modular surfaces (Centre de Recherches Mathématiques, Université de Montréal, Montréal, QC, 1992).Google Scholar
Larsen, M. J., Arithmetic compactification of some Shimura surfaces , in The zeta functions of Picard modular surfaces (Centre de Recherches Mathématiques, Université de Montréal, Montréal, QC, 1992), 31–45.Google Scholar
Liu, R., Triangulation of refined families , Comment. Math. Helv. 90 (2015), 831–904.10.4171/CMH/372Google Scholar
Matsushima, Y. and Murakami, S., On vector bundle valued harmonic forms and automorphic forms on symmetric Riemannian manifolds , Ann. of Math. (2) 78 (1963), 365–416.10.2307/1970348Google Scholar
Milne, J. S., Automorphic vector bundles on connected Shimura varieties , Invent. Math. 92 (1988), 91–128.10.1007/BF01393994Google Scholar
Pilloni, V., Formes modulaires surconvergentes , Ann. Inst. Fourier (Grenoble) 63 (2013), 219–239.10.5802/aif.2759Google Scholar
Pilloni, V. and Stroh, B., Surconvergence et classicité : le cas déployé, Preprint, (2012),http://perso.ens-lyon.fr/vincent.pilloni/.Google Scholar
Ribet, K. A., A modular construction of unramified p-extensions of Q (𝜇p) , Invent. Math. 34 (1976), 151–162.10.1007/BF01403065Google Scholar
Rogawski, J. D., Automorphic representations of unitary groups in three variables (Princeton University Press, Princeton, NJ, 1990).10.1515/9781400882441Google Scholar
Rogawski, J. D., The multiplicity formula for A-packets , in The zeta functions of Picard modular surfaces (Centre de Recherches Mathématiques, Université de Montréal, Montréal, QC, 1992), 395–419.Google Scholar
Rubin, K., The ‘main conjectures’ of Iwasawa theory for imaginary quadratic fields , Invent. Math. 103 (1991), 25–68.10.1007/BF01239508Google Scholar
Shimura, G., The arithmetic of automorphic forms with respect to a unitary group , Ann. of Math. (2) 107 (1978), 569–605.10.2307/1971129Google Scholar
Skinner, C., Galois representations associated with unitary groups over ℚ , Algebra Number Theory 6 (2012), 1697–1717.10.2140/ant.2012.6.1697Google Scholar
Skinner, C. and Urban, E., Sur les déformations p-adiques des formes de Saito-Kurokawa , C. R. Math. Acad. Sci. Paris 335 (2002), 581–586.10.1016/S1631-073X(02)02540-2Google Scholar
Stroh, B., Compactification de variétés de Siegel aux places de mauvaise réduction , Bull. Soc. Math. France 138 (2010), 259–315.10.24033/bsmf.2591Google Scholar
Urban, E., Eigenvarieties for reductive groups , Ann. of Math. (2) 174 (2011), 1685–1784.10.4007/annals.2011.174.3.7Google Scholar
Wallach, N. R., On the Selberg trace formula in the case of compact quotient , Bull. Amer. Math. Soc. 82 (1976), 171–195.10.1090/S0002-9904-1976-13979-1Google Scholar
Wedhorn, T., Ordinariness in good reductions of Shimura varieties of PEL-type , Ann. Sci. Éc. Norm. Supér. (4) 32 (1999), 575–618.10.1016/S0012-9593(01)80001-XGoogle Scholar
Wedhorn, T., The dimension of Oort strata of Shimura varieties of PEL-type , in Moduli of abelian varieties, Progress in Mathematics, vol. 195 (Birkhäuser, Basel, 2001), 441–471.10.1007/978-3-0348-8303-0_15Google Scholar
Yoshida, T., Week 2: Betti cohomology of Shimura varieties—the Matsushima formula, Preprint (2008), https://pdfs.semanticscholar.org/bd2a/305ad005e3d80d0775ee64996449e62c5189.pdf.Google Scholar