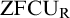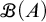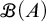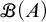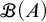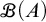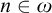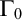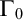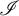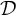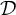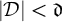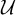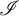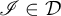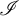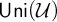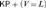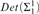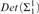19 results
AXIOMATIZATION AND FORCING IN SET THEORY WITH URELEMENTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
CANTOR’S THEOREM MAY FAIL FOR FINITARY PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
WAND/SET THEORIES: A REALIZATION OF CONWAY’S MATHEMATICIANS’ LIBERATION MOVEMENT, WITH AN APPLICATION TO CHURCH’S SET THEORY WITH A UNIVERSAL SET
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POINCARÉ–WEYL’S PREDICATIVITY: GOING BEYOND
 $\Gamma _{0}$
$\Gamma _{0}$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 41-91
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REFLECTION IN SECOND-ORDER SET THEORY WITH ABUNDANT URELEMENTS BI-INTERPRETS A SUPERCOMPACT CARDINAL
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 23 December 2022, pp. 1007-1043
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
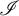 $\mathscr {I}$-ULTRAFILTERS IN THE RATIONAL PERFECT SET MODEL
$\mathscr {I}$-ULTRAFILTERS IN THE RATIONAL PERFECT SET MODEL
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 12 December 2022, pp. 175-194
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON DOUBLE-MEMBERSHIP GRAPHS OF MODELS OF ANTI-FOUNDATION
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 128-144
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TAKING REINHARDT’S POWER AWAY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 07 February 2022, pp. 1643-1662
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE COPERNICAN MULTIVERSE OF SETS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2021, pp. 1033-1069
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LEVEL THEORY, PART 1: AXIOMATIZING THE BARE IDEA OF A CUMULATIVE HIERARCHY OF SETS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 06 May 2021, pp. 436-460
- Print publication:
- December 2021
-
- Article
- Export citation
LEVEL THEORY, PART 2: AXIOMATIZING THE BARE IDEA OF A POTENTIAL HIERARCHY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 461-484
- Print publication:
- December 2021
-
- Article
- Export citation
LEVEL THEORY, PART 3: A BOOLEAN ALGEBRA OF SETS ARRANGED IN WELL-ORDERED LEVELS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 April 2021, pp. 1-26
- Print publication:
- March 2022
-
- Article
- Export citation
MITCHELL-INSPIRED FORCING, WITH SMALL WORKING PARTS AND COLLECTIONS OF MODELS OF UNIFORM SIZE AS SIDE CONDITIONS, AND GAP-ONE SIMPLIFIED MORASSES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 22 June 2020, pp. 392-415
- Print publication:
- March 2022
-
- Article
- Export citation
THE LARGE STRUCTURES OF GROTHENDIECK FOUNDED ON FINITE-ORDER ARITHMETIC
-
- Journal:
- The Review of Symbolic Logic / Volume 13 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 02 August 2019, pp. 296-325
- Print publication:
- June 2020
-
- Article
- Export citation
ALGEBRAIC NEW FOUNDATIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 05 February 2019, pp. 798-832
- Print publication:
- June 2019
-
- Article
- Export citation
CANTORIAN SET THEORY
-
- Journal:
- Bulletin of Symbolic Logic / Volume 24 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 02 January 2019, pp. 393-451
- Print publication:
- December 2018
-
- Article
- Export citation
MODAL STRUCTURALISM AND REFLECTION
-
- Journal:
- The Review of Symbolic Logic / Volume 12 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 14 June 2018, pp. 823-860
- Print publication:
- December 2019
-
- Article
- Export citation
ABOUT SOME FIXED POINT AXIOMS AND RELATED PRINCIPLES IN KRIPKE–PLATEK ENVIRONMENTS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 642-668
- Print publication:
- June 2018
-
- Article
- Export citation
HARRINGTON’S PRINCIPLE IN HIGHER ORDER ARITHMETIC
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 April 2015, pp. 477-489
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation