Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-22T22:46:03.397Z Has data issue: false hasContentIssue false
  • English
  • Français

AXIOMATIZATION AND FORCING IN SET THEORY WITH URELEMENTS

Part of: Set theory

Published online by Cambridge University Press:  11 November 2024

BOKAI YAO Open the ORCID record for BOKAI YAO [Opens in a new window]
BOKAI YAO*
Affiliation:
DEPARTMENT OF PHILOSOPHY AND RELIGIOUS STUDIES PEKING UNIVERSITY BEIJING CHINA URL: https://bokaiyao.com
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the first part of this paper, we consider several natural axioms in urelement set theory, including the Collection Principle, the Reflection Principle, the Dependent Choice scheme and its generalizations, as well as other axioms specifically concerning urelements. We prove that these axioms form a hierarchy over 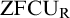$\text {ZFCU}_{\text {R}}$ (ZFC with urelements formulated with Replacement) in terms of direct implication. The second part of the paper studies forcing over countable transitive models of $\text {ZFU}_{\text {R}}$. We propose a new definition of 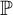${\mathbb P}$-names to address an issue with the existing approach. We then prove the fundamental theorem of forcing with urelements regarding axiom preservation. Moreover, we show that forcing can destroy and recover certain axioms within the previously established hierarchy. Finally, we demonstrate how ground model definability may fail when the ground model contains a proper class of urelements.

Keywords

urelementforcingZFUreflection principlesZFA

MSC classification

Primary: 03E30: Axiomatics of classical set theory and its fragments 03E40: Other aspects of forcing and Boolean-valued models
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 27
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Blass, A. and Ščedrov, A., Freyd’s Models for the Independence of the Axiom of Choice, vol. 404, American Mathematical Society, Providence, Rhode Island, 1989.Google Scholar
Farmer, S. (https://mathoverflow.net/users/160347/farmer-s), Does the axiom schema of collection imply schematic dependent choice in ZFCU? MathOverflow. Available at https://mathoverflow.net/q/387471 (version: 2021-03-27).Google Scholar
Felgner, U., Choice functions on sets and classes , Studies in Logic and the Foundations of Mathematics (J. B. Paris, editor), vol. 84, Elsevier, Amsterdam, 1976, pp. 217–255.Google Scholar
Friedman, S.-D., Gitman, V., and Kanovei, V., A model of second-order arithmetic satisfying AC but not DC . Journal of Mathematical Logic, vol. 19 (2019), no. 1, p. 1850013.CrossRefGoogle Scholar
Gitman, V., Hamkins, J. D., and Johnstone, T. A., What is the theory ZFC without power set? Mathematical Logic Quarterly, vol. 62 (2016), nos. 4–5, pp. 391–406.CrossRefGoogle Scholar
Hall, E. J., A characterization of permutation models in terms of forcing . Notre Dame Journal of Formal Logic, vol. 43 (2002), no. 3, pp. 157–168.CrossRefGoogle Scholar
Hall, E. J., Permutation models and SVC . Notre Dame Journal of Formal Logic, vol. 48 (2007), no. 2, pp. 229–235.CrossRefGoogle Scholar
Hamkins, J. D., Extensions with the approximation and cover properties have no new large cardinals . Fundamenta Mathematicae, vol. 180 (2003), pp. 257–277.CrossRefGoogle Scholar
Hamkins, J. D. and Yao, B., Reflection in second-order set theory with abundant urelements bi-interprets a supercompact cardinal, The Journal of Symbolic Logic (Jack J. Bulloff, Thomas C. Holyoke, Samuel W. Hahn, editors), Berlin, Published online (2022) pp. 1–37. doi:10.1017/jsl.2022.87.CrossRefGoogle Scholar
Jech, T. J.. The Axiom of Choice, Courier Corporation, Mineola, New York, 2008.Google Scholar
Kunen, K., Set Theory an Introduction to Independence Proofs, Elsevier, Strand, London, 2014.Google Scholar
Laver, R., Certain very large cardinals are not created in small forcing extensions . Annals of Pure and Applied Logic, vol. 149 (2007), nos. 1–3, pp. 1–6.CrossRefGoogle Scholar
Lévy, A., The interdependence of certain consequences of the axiom of choice . Fundamenta Mathematicae, vol. 53 (1964), pp. 135–157.CrossRefGoogle Scholar
Lévy, A., The definability of cardinal numbers , Foundations of Mathematics, Springer, 1969, pp. 15–38.CrossRefGoogle Scholar
Lévy, A. and Vaught, R., Principles of partial reflection in the set theories of Zermelo and Ackermann . Pacific Journal of Mathematics, vol. 11 (1961), no. 3, pp. 1045–1062.CrossRefGoogle Scholar
Monro, G. P., On generic extensions without the axiom of choice . Journal of Symbolic Logic, vol. 48 (1983), no. 1, pp. 39–52.CrossRefGoogle Scholar
Woodin, W. H., The continuum hypothesis, the generic-multiverse of sets, and the   $\Omega$  conjecture. Set Theory, Arithmetic, and Foundations of Mathematics: Theorems, Philosophies (Kennedy J, Kossak R, editors), Lecture Notes in Logic. Cambridge University Press; (2011) pp. 13–42.Google Scholar
Yao, B., Set Theory with Urelements, University of Notre Dame, Notre Dame, 2023.Google Scholar
Zarach, A. M., Replacement $\nrightarrow$ collection, Gödel’96: Logical Foundations of Mathematics, Computer Science and Physics—Kurt Gödel’s Legacy, Brno, Czech Republic, August 1996, Proceedings, vol. 6. Association for Symbolic Logic, Cambridge, 1996, pp. 307–323.Google Scholar