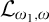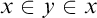Articles
WHICH CLASSES OF STRUCTURES ARE BOTH PSEUDO-ELEMENTARY AND DEFINABLE BY AN INFINITARY SENTENCE?
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2023, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LARGE CARDINALS AS PRINCIPLES OF STRUCTURAL REFLECTION
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2023, pp. 19-70
-
- Article
- Export citation
THE AXIOM OF CHOICE IS FALSE INTUITIONISTICALLY (IN MOST CONTEXTS)
- Part of:
-
- Published online by Cambridge University Press:
- 31 May 2022, pp. 71-96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTRUCTING NONSTANDARD HULLS AND LOEB MEASURES IN INTERNAL SET THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 14 December 2022, pp. 97-127
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON DOUBLE-MEMBERSHIP GRAPHS OF MODELS OF ANTI-FOUNDATION
- Part of:
-
- Published online by Cambridge University Press:
- 17 October 2022, pp. 128-144
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Meeting Report
ASSOCIATION FOR SYMBOLIC LOGIC
-
- Published online by Cambridge University Press:
- 15 March 2023, pp. 145-149
-
- Article
- Export citation
Announcement
NOTICES
-
- Published online by Cambridge University Press:
- 15 March 2023, pp. 150-156
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
BSL volume 29 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 15 March 2023, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
BSL volume 29 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 15 March 2023, pp. b1-b2
-
- Article
-
- You have access
- Export citation