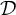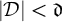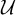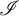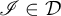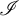1 Introduction
Let us recall some basic definitions. Given
![]() $f,g\in \omega ^{\omega }$
, we say that
$f,g\in \omega ^{\omega }$
, we say that
![]() $f\leq ^*g$
if the set
$f\leq ^*g$
if the set
![]() $\{n\in \omega : g(n)<f(n)\}$
is finite. Inclusion modulo finite is denoted by
$\{n\in \omega : g(n)<f(n)\}$
is finite. Inclusion modulo finite is denoted by
![]() $\subseteq ^*$
:
$\subseteq ^*$
:
![]() $A\subseteq ^*B$
if and only if
$A\subseteq ^*B$
if and only if
![]() $A\setminus B$
is finite. A filter on
$A\setminus B$
is finite. A filter on
![]() $\omega $
is a family
$\omega $
is a family
![]() $\mathcal {F}\subseteq \mathcal {P}(\omega )$
which is closed under finite intersections and supersets. An ultrafilter is a maximal filter with respect to the inclusion relation
$\mathcal {F}\subseteq \mathcal {P}(\omega )$
which is closed under finite intersections and supersets. An ultrafilter is a maximal filter with respect to the inclusion relation
![]() $\subseteq $
. An ideal is a family
$\subseteq $
. An ideal is a family
![]() $\mathscr {I}\subseteq \mathcal {P}(\omega )$
which is closed under finite unions and under subsets. We assume that all our filters are free, that is, for any filter
$\mathscr {I}\subseteq \mathcal {P}(\omega )$
which is closed under finite unions and under subsets. We assume that all our filters are free, that is, for any filter
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $\bigcap \mathcal {F}=\emptyset $
. On the other hand, we assume all our ideals are tall, which means that for any
$\bigcap \mathcal {F}=\emptyset $
. On the other hand, we assume all our ideals are tall, which means that for any
![]() $A\in [\omega ]^{\omega }$
, there is an infinite
$A\in [\omega ]^{\omega }$
, there is an infinite
![]() $B\subseteq A$
such that
$B\subseteq A$
such that
![]() $B\in \mathscr {I}$
. Also, we require that any ideal contains all the finite subsets of
$B\in \mathscr {I}$
. Also, we require that any ideal contains all the finite subsets of
![]() $\omega $
. If for any
$\omega $
. If for any
![]() $\langle A_n:n\in \omega \rangle \subseteq \mathscr {I}$
there is
$\langle A_n:n\in \omega \rangle \subseteq \mathscr {I}$
there is
![]() $B\in \mathscr {I}$
such that
$B\in \mathscr {I}$
such that
![]() $A_n\subseteq ^*B$
for all
$A_n\subseteq ^*B$
for all
![]() $n\in \omega $
, we say that
$n\in \omega $
, we say that
![]() $\mathscr {I}$
is a p-ideal.
$\mathscr {I}$
is a p-ideal.
The notion of filter and ideal are dual to each other in the following sense: let
![]() $\mathcal {F}$
be a filter on
$\mathcal {F}$
be a filter on
![]() $\omega $
, then
$\omega $
, then
![]() $\mathcal {F}^*=\{\omega \setminus A:A\in \mathcal {F}\}$
is an ideal. On the other hand, if
$\mathcal {F}^*=\{\omega \setminus A:A\in \mathcal {F}\}$
is an ideal. On the other hand, if
![]() $\mathscr {I}$
is an ideal on
$\mathscr {I}$
is an ideal on
![]() $\omega $
, then
$\omega $
, then
![]() $\mathscr {I}^*=\{\omega \setminus A:A\in \mathscr {I}\}$
is a filter. For any ideal
$\mathscr {I}^*=\{\omega \setminus A:A\in \mathscr {I}\}$
is a filter. For any ideal
![]() $\mathscr {I}$
, the family of
$\mathscr {I}$
, the family of
![]() $\mathscr {I}$
-positive sets, denoted by
$\mathscr {I}$
-positive sets, denoted by
![]() $\mathscr {I}^+$
, is the collection of all sets which are not elements of
$\mathscr {I}^+$
, is the collection of all sets which are not elements of
![]() $\mathscr {I}$
, that is,
$\mathscr {I}$
, that is,
![]() $\mathscr {I}^+=\mathcal {P}(\omega )\setminus \mathscr {I}$
.
$\mathscr {I}^+=\mathcal {P}(\omega )\setminus \mathscr {I}$
.
An ultrafilter
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\omega $
is rapid if for any function
$\omega $
is rapid if for any function
![]() $f\in \omega ^{\omega }$
, there is
$f\in \omega ^{\omega }$
, there is
![]() $A\in \mathcal {U}$
such that
$A\in \mathcal {U}$
such that
![]() $f\leq ^* e_A$
, where
$f\leq ^* e_A$
, where
![]() $e_A$
is the increasing enumeration of A. An ideal
$e_A$
is the increasing enumeration of A. An ideal
![]() $\mathscr {I}\subseteq \mathcal {P}(\omega )$
is summable if and only if there is a function
$\mathscr {I}\subseteq \mathcal {P}(\omega )$
is summable if and only if there is a function
![]() $g:\omega \to \mathbb {R}^+$
such that for all
$g:\omega \to \mathbb {R}^+$
such that for all
![]() $A\in \mathcal {P}(\omega )$
,
$A\in \mathcal {P}(\omega )$
,
![]() $A\in \mathscr {I}$
if and only of
$A\in \mathscr {I}$
if and only of
![]() $\sum _{n\in A}g(n)<\infty $
.
$\sum _{n\in A}g(n)<\infty $
.
Let us recall the following nice characterization of rapid ultrafilters due to P. Vojtáš:
Theorem 1.1 (Vojtáš, see [Reference Vojtáš15]).
An ultrafilter
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\omega $
is rapid if and only if
$\omega $
is rapid if and only if
![]() $\mathcal {U}$
has non-empty intersection with every summable ideal.
$\mathcal {U}$
has non-empty intersection with every summable ideal.
In [Reference Flašková8], among several results, J. Flašková proved the following refinement of Vojtáš theorem:
Theorem 1.2 (Flašková, see [Reference Flašková8]).
There is a family
![]() $\mathcal {D}$
of summable ideals with cardinality
$\mathcal {D}$
of summable ideals with cardinality
![]() $\mathfrak {d}$
Footnote
1
such that an ultrafilter is rapid if and only if it has non-empty intersection with every ideal from
$\mathfrak {d}$
Footnote
1
such that an ultrafilter is rapid if and only if it has non-empty intersection with every ideal from
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Then she asked the following question:
Question 1.3 (Flašková, see [Reference Flašková8]).
What is the minimal size of a family
![]() $\mathcal {D}$
of summable ideals such that an ultrafilter
$\mathcal {D}$
of summable ideals such that an ultrafilter
![]() $\mathcal {U}$
is rapid if and only if it has non-empty intersection with each ideal in
$\mathcal {U}$
is rapid if and only if it has non-empty intersection with each ideal in
![]() $\mathcal {D}$
?
$\mathcal {D}$
?
Let
![]() $\mathscr {I}$
be an ideal on
$\mathscr {I}$
be an ideal on
![]() $\omega $
. Given an ultrafilter
$\omega $
. Given an ultrafilter
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\omega $
, we say that
$\omega $
, we say that
![]() $\mathcal {U}$
is an
$\mathcal {U}$
is an
![]() $\mathscr {I}$
-ultrafilter if for any function
$\mathscr {I}$
-ultrafilter if for any function
![]() $f:\omega \to \omega $
there is
$f:\omega \to \omega $
there is
![]() $A\in \mathcal {U}$
such that
$A\in \mathcal {U}$
such that
![]() $f[A]\in \mathscr {I}$
. If we only require the previous property to hold only for finite to one functions, we say that
$f[A]\in \mathscr {I}$
. If we only require the previous property to hold only for finite to one functions, we say that
![]() $\mathcal {U}$
is a weak
$\mathcal {U}$
is a weak
![]() $\mathscr {I}$
-ultrafilter. The definition of
$\mathscr {I}$
-ultrafilter. The definition of
![]() $\mathscr {I}$
-ultrafilter was introduced by J. Baumgartner in [Reference Baumgartner3], and it has proved to be very useful in the classification of combinatorial properties of ultrafilters.
$\mathscr {I}$
-ultrafilter was introduced by J. Baumgartner in [Reference Baumgartner3], and it has proved to be very useful in the classification of combinatorial properties of ultrafilters.
In relation to
![]() $\mathscr {I}$
-ultrafilters, J. Flašková makes the following question which is a strengthening of the previous one.
$\mathscr {I}$
-ultrafilters, J. Flašková makes the following question which is a strengthening of the previous one.
![]() $\mathcal {D}$
denotes a family of summable ideals.
$\mathcal {D}$
denotes a family of summable ideals.
Question 1.4 (Flašková, see [Reference Flašková8]).
Is it true that whenever the cardinality of
![]() $\mathcal {D}$
is less than
$\mathcal {D}$
is less than
![]() $\mathfrak {d}$
, then there exist an ultrafilter on the natural numbers which is an
$\mathfrak {d}$
, then there exist an ultrafilter on the natural numbers which is an
![]() $\mathscr {I}_g$
-ultrafilter for every
$\mathscr {I}_g$
-ultrafilter for every
![]() $\mathscr {I}_g\in \mathcal {D}$
, but not a rapid ultrafilter?
$\mathscr {I}_g\in \mathcal {D}$
, but not a rapid ultrafilter?
By Theorem 1.2, we know that the answer to Question 1.3 is at most
![]() $\mathfrak {d}$
. In Section 3 of this paper we prove that in fact the equality holds. In Sections 4–6, we establish the consistency in the positive way of Question 1.4, showing that in the Rational Perfect set model, for any family
$\mathfrak {d}$
. In Section 3 of this paper we prove that in fact the equality holds. In Sections 4–6, we establish the consistency in the positive way of Question 1.4, showing that in the Rational Perfect set model, for any family
![]() $\mathcal {D}$
of summable ideals with cardinality less than
$\mathcal {D}$
of summable ideals with cardinality less than
![]() $\mathfrak {d}$
, there is an ultrafilter which is an
$\mathfrak {d}$
, there is an ultrafilter which is an
![]() $\mathscr {I}$
-ultrafilter for every
$\mathscr {I}$
-ultrafilter for every
![]() $\mathscr {I}\in \mathcal {D}$
, although there is no rapid ultrafilter in such model. This is done in two steps: the first one is proving that after forcing with the Rational Perfect set forcing, p-points which are
$\mathscr {I}\in \mathcal {D}$
, although there is no rapid ultrafilter in such model. This is done in two steps: the first one is proving that after forcing with the Rational Perfect set forcing, p-points which are
![]() $\mathscr {I}$
-ultrafilters continue to still generate p-point which are
$\mathscr {I}$
-ultrafilters continue to still generate p-point which are
![]() $\mathscr {I}$
-ultrafilters, whenever the ideal
$\mathscr {I}$
-ultrafilters, whenever the ideal
![]() $\mathscr {I}$
is an analytic p-ideal. The second step corresponds to prove a preservation theorem along countable support iterations of proper forcings which preserves p-points which are
$\mathscr {I}$
is an analytic p-ideal. The second step corresponds to prove a preservation theorem along countable support iterations of proper forcings which preserves p-points which are
![]() $\mathscr {I}$
-ultrafilters, for any
$\mathscr {I}$
-ultrafilters, for any
![]() $F_{\sigma } \ p$
-ideal
$F_{\sigma } \ p$
-ideal
![]() $\mathscr {I}$
. It turns out that the answer to Question 1.4 is independent of
$\mathscr {I}$
. It turns out that the answer to Question 1.4 is independent of
![]() $\mathsf {ZFC}$
: in [Reference Cancino-Manríquez7], it has been proved that it is relatively consistent with
$\mathsf {ZFC}$
: in [Reference Cancino-Manríquez7], it has been proved that it is relatively consistent with
![]() $\mathsf {ZFC}$
that there is no
$\mathsf {ZFC}$
that there is no
![]() $\mathscr {I}$
-ultrafilter for any
$\mathscr {I}$
-ultrafilter for any
![]() $F_{\sigma }$
ideal
$F_{\sigma }$
ideal
![]() $\mathscr {I}$
, which implies the consistency of a negative answer to Question 1.4.
$\mathscr {I}$
, which implies the consistency of a negative answer to Question 1.4.
As a consequence of our results, we generalize a theorem of T. Bartoszyński and S. Shelah. They proved that in the Rational Perfect set model, Hausdorff ultrafilters are dense in the Rudin–Blass ordering (see [Reference Bartoszyński and Shelah2]). We prove that in the same model,
![]() $\mathscr {I}$
-ultrafilters are dense, for any analytic p-ideal
$\mathscr {I}$
-ultrafilters are dense, for any analytic p-ideal
![]() $\mathscr {I}$
. This result has the interesting consequence that it can not be proved, in
$\mathscr {I}$
. This result has the interesting consequence that it can not be proved, in
![]() $\mathsf {ZFC}$
alone, the existence of an ultrafilter
$\mathsf {ZFC}$
alone, the existence of an ultrafilter
![]() $\mathcal {U}$
none of whose Rudin–Blass predecessors are
$\mathcal {U}$
none of whose Rudin–Blass predecessors are
![]() $\mathscr {I}$
-ultrafilters for any analytic p-ideal. This result contrasts with a theorem of C. Laflamme and J. Zhu, which states, in
$\mathscr {I}$
-ultrafilters for any analytic p-ideal. This result contrasts with a theorem of C. Laflamme and J. Zhu, which states, in
![]() $\mathsf {ZFC}$
, the existence of an ultrafilter
$\mathsf {ZFC}$
, the existence of an ultrafilter
![]() $\mathcal {U}$
none of whose Rudin–Blass predecessors are rapid ultrafilters (see [Reference Laflamme and Zhu11]). In particular, none of them are weak
$\mathcal {U}$
none of whose Rudin–Blass predecessors are rapid ultrafilters (see [Reference Laflamme and Zhu11]). In particular, none of them are weak
![]() $\mathcal {ED}_{fin}$
-ultrafilters, i.e., q-points. In Section 7, we discuss these facts in more detail.
$\mathcal {ED}_{fin}$
-ultrafilters, i.e., q-points. In Section 7, we discuss these facts in more detail.
2 Preliminaries
Let us recall that a family of functions
![]() $\mathcal {D}\subseteq \omega ^{\omega }$
is a dominating family, if for any
$\mathcal {D}\subseteq \omega ^{\omega }$
is a dominating family, if for any
![]() $g\in \omega ^{\omega }$
, there is
$g\in \omega ^{\omega }$
, there is
![]() $f\in \mathcal {D}$
such that
$f\in \mathcal {D}$
such that
![]() $g\leq ^*f$
. The dominating number is defined as the minimal possible cardinality of a dominating family:
$g\leq ^*f$
. The dominating number is defined as the minimal possible cardinality of a dominating family:
An ideal
![]() $\mathscr {I}$
on
$\mathscr {I}$
on
![]() $\omega $
is a p-ideal if for any
$\omega $
is a p-ideal if for any
![]() $\langle A_n:n\in \omega \rangle \subseteq \mathscr {I}$
there is
$\langle A_n:n\in \omega \rangle \subseteq \mathscr {I}$
there is
![]() $B\in \mathscr {I}$
such that for all
$B\in \mathscr {I}$
such that for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $A_n\subseteq ^* B$
.
$A_n\subseteq ^* B$
.
An ultrafilter on
![]() $\omega $
is called a p-point if for any sequence
$\omega $
is called a p-point if for any sequence
![]() $\langle A_n:n\in \omega \rangle $
of elements from
$\langle A_n:n\in \omega \rangle $
of elements from
![]() $\mathcal {U}$
, there is
$\mathcal {U}$
, there is
![]() $A\in \mathcal {U}$
such that for all
$A\in \mathcal {U}$
such that for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $A\subseteq ^*A_n$
. There is a nice characterization of p-points by mean of infinite games which we will make use of:
$A\subseteq ^*A_n$
. There is a nice characterization of p-points by mean of infinite games which we will make use of:
Definition 2.1 (p-point game).
Given an ultrafilter
![]() $\mathcal {U}$
, the two players game
$\mathcal {U}$
, the two players game
![]() $G(\mathcal {U})$
is defined as a sequence of choices were, at round n, Player I chooses an element from the ultrafilter,
$G(\mathcal {U})$
is defined as a sequence of choices were, at round n, Player I chooses an element from the ultrafilter,
![]() $A_n\in \mathcal {U}$
, and Player II chooses a finite subset
$A_n\in \mathcal {U}$
, and Player II chooses a finite subset
![]() $F_n\in [A_n]^{<\omega }$
, and Player II wins if and only if
$F_n\in [A_n]^{<\omega }$
, and Player II wins if and only if
![]() $\bigcup _{n\in \omega } F_n\in \mathcal {U}$
:
$\bigcup _{n\in \omega } F_n\in \mathcal {U}$
:

The following well known characterization of p-points will be used in the proof of Theorem 4.8.
Lemma 2.2 (Laflamme, see [Reference Laflamme10]).
Let
![]() $\mathcal {U}$
be an ultrafilter on
$\mathcal {U}$
be an ultrafilter on
![]() $\omega $
. Then
$\omega $
. Then
![]() $\mathcal {U}$
is a p-point if and only if Player I has no winning strategy in the p-point game.
$\mathcal {U}$
is a p-point if and only if Player I has no winning strategy in the p-point game.
Proof The reader can find a proof in Laflamme’s article [Reference Laflamme10]. Another good reference is found in Wohofsky master’s thesis [Reference Wohofsky16, pp. 53–59].
Let us recall the Rational Perfect set forcing. The family of all finite sequences of natural numbers will be denoted by
![]() $\omega ^{<\omega }$
. For any
$\omega ^{<\omega }$
. For any
![]() $s\in \omega ^{<\omega }$
, the length of the sequence s is defined as its cardinaliy, and will be denoted by
$s\in \omega ^{<\omega }$
, the length of the sequence s is defined as its cardinaliy, and will be denoted by
![]() $\vert s\vert $
. For
$\vert s\vert $
. For
![]() $s\in \omega ^{<\omega }$
and
$s\in \omega ^{<\omega }$
and
![]() $i\in \omega $
, denote by
$i\in \omega $
, denote by
![]() $s^{\frown } i$
the sequence obtained by adding i to the end of the sequence s. A subset
$s^{\frown } i$
the sequence obtained by adding i to the end of the sequence s. A subset
![]() $T\subseteq \omega ^{<\omega }$
is a tree if for any
$T\subseteq \omega ^{<\omega }$
is a tree if for any
![]() $s\in T$
and
$s\in T$
and
![]() $i\leq \vert s\vert $
, we have
$i\leq \vert s\vert $
, we have
![]() $s\upharpoonright i\in T$
. For a tree
$s\upharpoonright i\in T$
. For a tree
![]() $T\subseteq \omega ^{<\omega }$
and
$T\subseteq \omega ^{<\omega }$
and
![]() $s\in T$
, we say that
$s\in T$
, we say that
![]() $i\in \omega $
is an immediate successor of s in T if
$i\in \omega $
is an immediate successor of s in T if
![]() $s^{\frown } i\in T$
. The set of all immediate successors of s in T will be denoted by
$s^{\frown } i\in T$
. The set of all immediate successors of s in T will be denoted by
![]() $succ_{T}(s)=\{i\in \omega :i\text { is an immediate successor of}\ s \text { in } T\}$
. A node
$succ_{T}(s)=\{i\in \omega :i\text { is an immediate successor of}\ s \text { in } T\}$
. A node
![]() $s\in T$
is an splitting node if it has more than one successor in T, that is
$s\in T$
is an splitting node if it has more than one successor in T, that is
![]() $\vert succ_T(s)\vert>1$
, and the set of all splitting nodes of T is denote by
$\vert succ_T(s)\vert>1$
, and the set of all splitting nodes of T is denote by
![]() $split(T)$
. For a tree T and a node
$split(T)$
. For a tree T and a node
![]() $s\in T$
,
$s\in T$
,
![]() $T\upharpoonright s$
denotes the tree of all nodes in T which are
$T\upharpoonright s$
denotes the tree of all nodes in T which are
![]() $\subseteq $
-comparable with s.
$\subseteq $
-comparable with s.
A superperfect tree tree
![]() $T\subseteq \omega ^{<\omega }$
is a non-empty tree satisfying the following properties:
$T\subseteq \omega ^{<\omega }$
is a non-empty tree satisfying the following properties:
-
(1) For all
 $s\in T$
, there is
$s\in T$
, there is
 $t\in split(T)$
such that
$t\in split(T)$
such that
 $s\subseteq t$
.
$s\subseteq t$
. -
(2) For all
 $s\in split(T)$
, s has infinitely many immediate successors.
$s\in split(T)$
, s has infinitely many immediate successors.
The Rational Perfect set forcing, denoted by
![]() $\mathbf {PT}$
, is the partial order whose members are all the superperfect trees, with the order given by set inclusion, that is
$\mathbf {PT}$
, is the partial order whose members are all the superperfect trees, with the order given by set inclusion, that is
![]() $S\leq T$
if and only if
$S\leq T$
if and only if
![]() $S\subseteq T$
.
$S\subseteq T$
.
For
![]() $T\in \mathbf {PT}$
, the stem of T, denoted by
$T\in \mathbf {PT}$
, the stem of T, denoted by
![]() $st(T)$
, is defined as the unique node in
$st(T)$
, is defined as the unique node in
![]() $split(T)$
of minimal length.
$split(T)$
of minimal length.
Given a superperfect tree T, define an order isomorphism between
![]() $\omega ^{<\omega }$
and
$\omega ^{<\omega }$
and
![]() $split(T)$
, which we denote by
$split(T)$
, which we denote by
![]() $\varphi _T$
, as follows:
$\varphi _T$
, as follows:
![]() $\varphi _T(\emptyset )=st(T)$
; assume
$\varphi _T(\emptyset )=st(T)$
; assume
![]() $\varphi _T(s)$
is defined and let
$\varphi _T(s)$
is defined and let
![]() $\{i_k:k\in \omega \}$
be the increasing enumeration of
$\{i_k:k\in \omega \}$
be the increasing enumeration of
![]() $succ_{T}(\varphi _T(s))$
, for each
$succ_{T}(\varphi _T(s))$
, for each
![]() $k\in \omega $
let
$k\in \omega $
let
![]() $r_{s,k}\in split(T)$
be the node of minimal length extending
$r_{s,k}\in split(T)$
be the node of minimal length extending
![]() $\varphi _T(s)^{\frown } i_k$
, and define
$\varphi _T(s)^{\frown } i_k$
, and define
![]() $\varphi _T(s^{\frown } k)=r_{s,k}$
.
$\varphi _T(s^{\frown } k)=r_{s,k}$
.
An ideal
![]() $\mathscr {I}$
on
$\mathscr {I}$
on
![]() $\omega $
is a summable ideal if there exists
$\omega $
is a summable ideal if there exists
![]() $g:\omega \to \mathbb {R}^+$
such that
$g:\omega \to \mathbb {R}^+$
such that
![]() $A\in \mathscr {I}$
if and only if
$A\in \mathscr {I}$
if and only if
![]() $\sum _{n\in A}g(n)<\infty $
. For a given
$\sum _{n\in A}g(n)<\infty $
. For a given
![]() $g:\omega \to \mathbb {R}^+$
, we denote by
$g:\omega \to \mathbb {R}^+$
, we denote by
![]() $\mathscr {I}_g$
the summable ideal defined by g. Note that since we are assuming all our ideals are tall, it should hold that
$\mathscr {I}_g$
the summable ideal defined by g. Note that since we are assuming all our ideals are tall, it should hold that
![]() $\lim _{n\to \infty }g(n)=0$
whenever g defines a summable ideal.
$\lim _{n\to \infty }g(n)=0$
whenever g defines a summable ideal.
Recall that a function
![]() $\varphi :\mathcal {P}(\omega )\to [0,\infty ]$
is a lower semicontinuous submeasure, lscsm for short, if it satisfies the following properties:
$\varphi :\mathcal {P}(\omega )\to [0,\infty ]$
is a lower semicontinuous submeasure, lscsm for short, if it satisfies the following properties:
-
(1)
 $\varphi (\emptyset )=0$
.
$\varphi (\emptyset )=0$
. -
(2) For all
 $A,B\in \mathcal {P}(\omega )$
, if
$A,B\in \mathcal {P}(\omega )$
, if
 $A\subseteq B$
, then
$A\subseteq B$
, then
 $\varphi (A)\leq \varphi (B)$
.
$\varphi (A)\leq \varphi (B)$
. -
(3) For all
 $A,B\in \mathcal {P}(\omega )$
,
$A,B\in \mathcal {P}(\omega )$
,
 $\varphi (A\cup B)\leq \varphi (A)+\varphi (B)$
.
$\varphi (A\cup B)\leq \varphi (A)+\varphi (B)$
. -
(4) For all
 $A\in \mathcal {P}(\omega )$
,
$A\in \mathcal {P}(\omega )$
,
 $\lim _{n\to \infty }\varphi (A\cap n)=\varphi (A)$
.
$\lim _{n\to \infty }\varphi (A\cap n)=\varphi (A)$
.
Given
![]() $\varphi $
a lscsm, there are two ideals associated with
$\varphi $
a lscsm, there are two ideals associated with
![]() $\varphi $
:
$\varphi $
:
-
(1)
 $Fin(\varphi )=\{A\in \mathcal {P}(\omega ):\varphi (A)<\infty \}$
.
$Fin(\varphi )=\{A\in \mathcal {P}(\omega ):\varphi (A)<\infty \}$
. -
(2)
 $Exh(\varphi )=\{A\in \mathcal {P}(\omega ):\lim _{n\to \infty }\varphi (A\setminus n)=0\}$
.
$Exh(\varphi )=\{A\in \mathcal {P}(\omega ):\lim _{n\to \infty }\varphi (A\setminus n)=0\}$
.
The following well known theorem will be necessary in Sections 4–6:
Theorem 2.3.
-
(1) (Solecki, see [Reference Solecki14]) An ideal
 $\mathscr {I}$
is an analytic p-ideal if and only if there is a lscsm
$\mathscr {I}$
is an analytic p-ideal if and only if there is a lscsm
 $\varphi $
such that
$\varphi $
such that
 $\mathscr {I}=Exh(\varphi )$
.
$\mathscr {I}=Exh(\varphi )$
. -
(2) (Mazur, see [Reference Mazur12]) An ideal
 $\mathscr {I}$
is an
$\mathscr {I}$
is an
 $F_{\sigma }$
ideal if and only if there is a lscsm
$F_{\sigma }$
ideal if and only if there is a lscsm
 $\varphi $
such that
$\varphi $
such that
 $\mathscr {I}=Fin(\varphi )$
.
$\mathscr {I}=Fin(\varphi )$
. -
(3) (Solecki, see [Reference Solecki14]) An ideal
 $\mathscr {I}$
is an
$\mathscr {I}$
is an
 $F_{\sigma } \ p$
-ideal if and only if there is a lscsm
$F_{\sigma } \ p$
-ideal if and only if there is a lscsm
 $\varphi $
such that
$\varphi $
such that
 $\mathscr {I}=Fin(\varphi )=Exh(\varphi )$
.
$\mathscr {I}=Fin(\varphi )=Exh(\varphi )$
.
Note that given a lscsm
![]() $\varphi :\mathcal {P}(\omega )\to [0,\infty ]$
, the lower semicontinuity implies that
$\varphi :\mathcal {P}(\omega )\to [0,\infty ]$
, the lower semicontinuity implies that
![]() $\varphi $
is determined by its values on the finite sets, in the sense that for any
$\varphi $
is determined by its values on the finite sets, in the sense that for any
![]() $A\in [\omega ]^{\omega }$
,
$A\in [\omega ]^{\omega }$
,
![]() $\varphi (A)=\lim _{n\to \infty }\varphi (A\cap n)$
. In this way, if
$\varphi (A)=\lim _{n\to \infty }\varphi (A\cap n)$
. In this way, if
![]() $\varphi $
is defined in the ground model V, and
$\varphi $
is defined in the ground model V, and
![]() $V[\dot {G}]$
is a generic extension of V, we can extend
$V[\dot {G}]$
is a generic extension of V, we can extend
![]() $\varphi $
to the whole
$\varphi $
to the whole
![]() $\mathcal {P}(\omega )^{V[\dot {G}]}$
by setting
$\mathcal {P}(\omega )^{V[\dot {G}]}$
by setting
![]() $\varphi (A)=\lim _{n\to \infty }\varphi (A\cap n)$
, for any
$\varphi (A)=\lim _{n\to \infty }\varphi (A\cap n)$
, for any
![]() $A\in \mathcal {P}(\omega )^{V[\dot {G}]}$
. Then, in
$A\in \mathcal {P}(\omega )^{V[\dot {G}]}$
. Then, in
![]() $V[\dot {G}]$
,
$V[\dot {G}]$
,
![]() $\varphi $
defines an
$\varphi $
defines an
![]() $F_{\sigma }$
ideal which extends
$F_{\sigma }$
ideal which extends
![]() $Fin(\varphi )^{V}$
, and moreover, the
$Fin(\varphi )^{V}$
, and moreover, the
![]() $\varphi $
-measure computed in V and
$\varphi $
-measure computed in V and
![]() $V[\dot {G}]$
agrees for any
$V[\dot {G}]$
agrees for any
![]() $A\in \mathcal {P}(\omega )^{V}$
. A similar remark holds for
$A\in \mathcal {P}(\omega )^{V}$
. A similar remark holds for
![]() $F_{\sigma \delta }$
ideals of the form
$F_{\sigma \delta }$
ideals of the form
![]() $Exh(\varphi )$
. Following this remark, whenever we have an
$Exh(\varphi )$
. Following this remark, whenever we have an
![]() $F_{\sigma }$
(resp.
$F_{\sigma }$
(resp.
![]() $F_{\sigma \delta }$
) ideal (resp. p-ideal)
$F_{\sigma \delta }$
) ideal (resp. p-ideal)
![]() $\mathscr {I}$
in the ground model, and we talk about such ideal in a generic extension, we mean the ideal computed by any lscsm which defines
$\mathscr {I}$
in the ground model, and we talk about such ideal in a generic extension, we mean the ideal computed by any lscsm which defines
![]() $\mathscr {I}$
. A similar remark holds for ideals arising along a forcing iteration.
$\mathscr {I}$
. A similar remark holds for ideals arising along a forcing iteration.
Finally, let us recall some concepts and results about the theory of proper forcing.
Definition 2.4. Let
![]() $\mathbb {P}$
be a forcing and
$\mathbb {P}$
be a forcing and
![]() $\theta>2^{\vert \mathbb {P}\vert }$
a cardinal. Let
$\theta>2^{\vert \mathbb {P}\vert }$
a cardinal. Let
![]() $\mathcal {M}\prec H(\theta )$
be countable elementary submodel such that
$\mathcal {M}\prec H(\theta )$
be countable elementary submodel such that
![]() $\mathbb {P}\in \mathcal {M}$
. A condition
$\mathbb {P}\in \mathcal {M}$
. A condition
![]() $q\in \mathbb {P}$
is called an
$q\in \mathbb {P}$
is called an
![]() $(\mathcal {M},\mathbb {P})$
-generic condition if
$(\mathcal {M},\mathbb {P})$
-generic condition if
![]() $\mathbb {P}\cap \mathcal {M}$
is predense below q.
$\mathbb {P}\cap \mathcal {M}$
is predense below q.
Definition 2.5. Let
![]() $\mathbb {P}$
be a forcing notion.
$\mathbb {P}$
be a forcing notion.
![]() $\mathbb {P}$
is proper if for any
$\mathbb {P}$
is proper if for any
![]() $\theta> 2^{\vert \mathbb {P}\vert }$
and any countable elementary submodel
$\theta> 2^{\vert \mathbb {P}\vert }$
and any countable elementary submodel
![]() $\mathcal {M}\prec H(\theta )$
such that
$\mathcal {M}\prec H(\theta )$
such that
![]() $\mathbb {P}\in \mathcal {M}$
, any condition
$\mathbb {P}\in \mathcal {M}$
, any condition
![]() $p\in \mathcal {M}$
has an
$p\in \mathcal {M}$
has an
![]() $(\mathcal {M},\mathbb {P})$
-generic extension
$(\mathcal {M},\mathbb {P})$
-generic extension
![]() $q\leq p$
.
$q\leq p$
.
The following well known results will be used in the proofs of Lemma 5.5 and Theorem 5.1 without explicit mention.
Lemma 2.6. Let
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
be a two step iteration forcing,
$\mathbb {P}*\dot {\mathbb {Q}}$
be a two step iteration forcing,
![]() $\theta $
a sufficiently large cardinal, and let
$\theta $
a sufficiently large cardinal, and let
![]() $\mathcal {M}\prec H(\theta )$
be countable elementary submodel such that
$\mathcal {M}\prec H(\theta )$
be countable elementary submodel such that
![]() $\mathbb {P}*\dot {\mathbb {Q}}\in \mathcal {M}$
. A condition
$\mathbb {P}*\dot {\mathbb {Q}}\in \mathcal {M}$
. A condition
![]() $(p,\dot {q})$
is an
$(p,\dot {q})$
is an
![]() $(\mathcal {M},\mathbb {P}*\dot {\mathbb {Q}})$
-generic condition if and only if p is
$(\mathcal {M},\mathbb {P}*\dot {\mathbb {Q}})$
-generic condition if and only if p is
![]() $(\mathcal {M},\mathbb {P})$
-generic and
$(\mathcal {M},\mathbb {P})$
-generic and
where
![]() $\dot {G}$
is the canonical name for the generic filter for
$\dot {G}$
is the canonical name for the generic filter for
![]() $\mathbb {P}$
over V.
$\mathbb {P}$
over V.
Theorem 2.7. Let
![]() $\mathbb {P}=\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\alpha }:\alpha <\gamma \rangle $
be a countable support iteration such that
$\mathbb {P}=\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\alpha }:\alpha <\gamma \rangle $
be a countable support iteration such that
![]() $\mathbb {P}_0$
is proper and for all
$\mathbb {P}_0$
is proper and for all
![]() $\alpha <\gamma $
,
$\alpha <\gamma $
,
![]() $\mathbb {P}_{\alpha }\Vdash ` `\dot {\mathbb {Q}}_{\alpha }\text { is proper}"$
. Then
$\mathbb {P}_{\alpha }\Vdash ` `\dot {\mathbb {Q}}_{\alpha }\text { is proper}"$
. Then
![]() $\mathbb {P}$
is proper.
$\mathbb {P}$
is proper.
Theorem 2.8 (Blass and Shelah, see [Reference Blass and Shelah5]).
Let
![]() $\kern1.5pt\mathcal {U}$
be a p-point, and let
$\kern1.5pt\mathcal {U}$
be a p-point, and let
![]() $\mathbb {P}=\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\alpha }:\alpha <\gamma \rangle $
be a countable support iteration of proper forcings such that for all
$\mathbb {P}=\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\alpha }:\alpha <\gamma \rangle $
be a countable support iteration of proper forcings such that for all
![]() $\alpha <\gamma $
,
$\alpha <\gamma $
,
![]() $\mathbb {P}_{\alpha }\Vdash ` `\dot {\mathbb {Q}}_{\alpha }\text { forces that } \mathcal {U} \text { generates a } p\text {-point}"$
. Then after forcing with
$\mathbb {P}_{\alpha }\Vdash ` `\dot {\mathbb {Q}}_{\alpha }\text { forces that } \mathcal {U} \text { generates a } p\text {-point}"$
. Then after forcing with
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\mathcal {U}$
generates a p-point.
$\mathcal {U}$
generates a p-point.
3
 $\mathfrak {d}$
is the best
$\mathfrak {d}$
is the best
For the sake of simplicity, let us say that a family
![]() $\mathcal {D}$
of summable ideals is a Vojtáš family if an ultrafilter is rapid if and only if it has non-empty intersection with each member from
$\mathcal {D}$
of summable ideals is a Vojtáš family if an ultrafilter is rapid if and only if it has non-empty intersection with each member from
![]() $\mathcal {D}$
. The main theorem of this section can be stated as follows:
$\mathcal {D}$
. The main theorem of this section can be stated as follows:
Theorem 3.1.
![]() $\mathfrak {d}$
is equal to the minimum cardinality of a Vojtáš family.
$\mathfrak {d}$
is equal to the minimum cardinality of a Vojtáš family.
Since Theorem 1.2 means that
![]() $\mathfrak {d}$
is an upper bound for the minimum cardinality of a Vojtáš family, we only have to prove the following:
$\mathfrak {d}$
is an upper bound for the minimum cardinality of a Vojtáš family, we only have to prove the following:
Proposition 3.2. There is no Vojtáš family
![]() $\mathcal {D}$
of cardinality strictly smaller than
$\mathcal {D}$
of cardinality strictly smaller than
![]() $\mathfrak {d}$
.
$\mathfrak {d}$
.
Proof It is enough to prove that given any non-empty family of summable ideals of cardinality less than
![]() $\mathfrak {d}$
, there is an ultrafilter meeting each ideal in the family, but still there is a tall summable ideal having empty intersection with the ultrafilter. Fix
$\mathfrak {d}$
, there is an ultrafilter meeting each ideal in the family, but still there is a tall summable ideal having empty intersection with the ultrafilter. Fix
![]() $\mathcal {D}=\{\mathscr {I}_{\alpha }:\alpha <\lambda \}$
an arbitrary family of tall summable ideals such that
$\mathcal {D}=\{\mathscr {I}_{\alpha }:\alpha <\lambda \}$
an arbitrary family of tall summable ideals such that
![]() $\lambda <\mathfrak {d}$
, and for
$\lambda <\mathfrak {d}$
, and for
![]() $\alpha \in \lambda $
, let
$\alpha \in \lambda $
, let
![]() $g_{\alpha }:\omega \to \mathbb R$
be a function such that
$g_{\alpha }:\omega \to \mathbb R$
be a function such that
![]() $\mathscr {I}_{\alpha }=\{A\in \mathcal {P}(\omega ):\sum _{n\in A}g_{\alpha }(n)<\infty \}$
. Let E be the set of even natural numbers. For each
$\mathscr {I}_{\alpha }=\{A\in \mathcal {P}(\omega ):\sum _{n\in A}g_{\alpha }(n)<\infty \}$
. Let E be the set of even natural numbers. For each
![]() $F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}$
, define a function
$F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}$
, define a function
![]() $\psi _F$
on E as follows:
$\psi _F$
on E as follows:
 $$ \begin{align*} &\qquad\qquad\qquad\qquad\qquad\qquad \psi_F(0)=0,\\ &\psi_{F}(n+2)=\min\{k\in\omega:k>\psi_{F}(n)\ \text{and}\ (\forall\alpha\in F)(\forall i\ge k)\\ &\qquad\qquad\qquad\qquad\quad(g_{\alpha}(i)\leq1/2^{n+2}(n+2)^{2})\}. \end{align*} $$
$$ \begin{align*} &\qquad\qquad\qquad\qquad\qquad\qquad \psi_F(0)=0,\\ &\psi_{F}(n+2)=\min\{k\in\omega:k>\psi_{F}(n)\ \text{and}\ (\forall\alpha\in F)(\forall i\ge k)\\ &\qquad\qquad\qquad\qquad\quad(g_{\alpha}(i)\leq1/2^{n+2}(n+2)^{2})\}. \end{align*} $$
Since
![]() $\{\psi _{F}:F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}\}$
has cardinality less than
$\{\psi _{F}:F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}\}$
has cardinality less than
![]() $\mathfrak {d}$
, there is a function
$\mathfrak {d}$
, there is a function
![]() $f:E\to \omega $
which is not dominated by
$f:E\to \omega $
which is not dominated by
![]() $\{\psi _{F}:F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}\}$
. We can assume that for all
$\{\psi _{F}:F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}\}$
. We can assume that for all
![]() $n\in E$
,
$n\in E$
,
![]() $f(n+2)-f(n)>n^{2}$
, and we can define the following function:
$f(n+2)-f(n)>n^{2}$
, and we can define the following function:
 $$ \begin{align*} \tilde{f}(n)=\begin{cases} f(n),\text{ if }n\in E,\\ f(n-1)+(n-1)^{2}, \quad \text{if }n\notin E. \end{cases} \end{align*} $$
$$ \begin{align*} \tilde{f}(n)=\begin{cases} f(n),\text{ if }n\in E,\\ f(n-1)+(n-1)^{2}, \quad \text{if }n\notin E. \end{cases} \end{align*} $$
For each
![]() $F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}$
, let
$F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}$
, let
![]() $A_{F}$
be the set where
$A_{F}$
be the set where
![]() $\psi _{F}$
is dominated by f, that is
$\psi _{F}$
is dominated by f, that is
![]() $A_{F}=\{n\in E:\psi _{F}(n)\leq f(n)\}$
. Note that the family
$A_{F}=\{n\in E:\psi _{F}(n)\leq f(n)\}$
. Note that the family
![]() $\{A_{F}:F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}\}$
is a centered family. Indeed, pick
$\{A_{F}:F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}\}$
is a centered family. Indeed, pick
![]() $F_{0},\ldots ,F_{n}\in [\lambda ]^{<\omega }\setminus \{\emptyset \}$
. By the definition of the functions
$F_{0},\ldots ,F_{n}\in [\lambda ]^{<\omega }\setminus \{\emptyset \}$
. By the definition of the functions
![]() $\psi _{F}$
we have that if
$\psi _{F}$
we have that if
![]() $F\subseteq G$
, then
$F\subseteq G$
, then
![]() $\psi _{F}\leq \psi _{G}$
, so in particular, if
$\psi _{F}\leq \psi _{G}$
, so in particular, if
![]() $\psi _{F_{0}\cup \cdots \cup F_{n}}(k)\leq f(k)$
, then we have
$\psi _{F_{0}\cup \cdots \cup F_{n}}(k)\leq f(k)$
, then we have
![]() $\psi _{F_{i}}(k)\leq f(k)$
for
$\psi _{F_{i}}(k)\leq f(k)$
for
![]() $i=0,\ldots ,n$
, and so
$i=0,\ldots ,n$
, and so
![]() $k\in A_{0}\cap \cdots \cap A_{n}$
.
$k\in A_{0}\cap \cdots \cap A_{n}$
.
Now, for
![]() $F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}$
let
$F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}$
let
![]() $B_{F}$
be the set
$B_{F}$
be the set
![]() $\bigcup _{k\in A_{F}}[\tilde {f}(k),\tilde{f}(k+1))$
. Finally, take the family
$\bigcup _{k\in A_{F}}[\tilde {f}(k),\tilde{f}(k+1))$
. Finally, take the family
![]() $\mathcal {G}=\{B_{F}:F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}\}$
. It follows that
$\mathcal {G}=\{B_{F}:F\in [\lambda ]^{<\omega }\setminus \{\emptyset \}\}$
. It follows that
![]() $\mathcal {G}$
is a centered family, by the previous paragraph.
$\mathcal {G}$
is a centered family, by the previous paragraph.
Let us see that
![]() $\mathcal {G}$
has non-empty intersection with each ideal in
$\mathcal {G}$
has non-empty intersection with each ideal in
![]() $\mathcal {D}$
. For
$\mathcal {D}$
. For
![]() $\alpha \in \lambda $
, we claim that
$\alpha \in \lambda $
, we claim that
![]() $B_{\{\alpha \}}\in \mathscr {I}_{\alpha }$
. This follows easily from the definition of
$B_{\{\alpha \}}\in \mathscr {I}_{\alpha }$
. This follows easily from the definition of
![]() ${\psi _{\{\alpha \}}}$
and
${\psi _{\{\alpha \}}}$
and
![]() ${A_{\{\alpha \}}}$
. We have that for all
${A_{\{\alpha \}}}$
. We have that for all
![]() ${n\in A_{\{\alpha \}}}$
,
${n\in A_{\{\alpha \}}}$
,
![]() ${\psi _{\{\alpha \}}(n)\leq f(n)=\tilde {f}(n)}$
, and by the definition of
${\psi _{\{\alpha \}}(n)\leq f(n)=\tilde {f}(n)}$
, and by the definition of
![]() ${\psi _{\{\alpha \}}}$
, for every
${\psi _{\{\alpha \}}}$
, for every
![]() ${k\ge \psi _{\{\alpha \}}(n)}$
,
${k\ge \psi _{\{\alpha \}}(n)}$
,
![]() ${g_{\alpha }(k)\leq \frac {1}{2^{n}n^{2}}}$
, so in particular, for every
${g_{\alpha }(k)\leq \frac {1}{2^{n}n^{2}}}$
, so in particular, for every
![]() ${n\in A_{\{\alpha \}}}$
and every
${n\in A_{\{\alpha \}}}$
and every
![]() ${k\ge \tilde {f}(n)},{\ g_{\alpha }(k)\leq \frac {1}{2^{n}n^{2}}}$
. We have the following:
${k\ge \tilde {f}(n)},{\ g_{\alpha }(k)\leq \frac {1}{2^{n}n^{2}}}$
. We have the following:
 $$ \begin{align*} \sum_{n\in B_{\{\alpha\}}} g_{\alpha}(n)&=\sum_{n\in A_{\{\alpha\}}} \left[\sum_{m\in[\tilde{f}(n),\tilde{f}(n+1))}g_{\alpha}(m)\right]\\ &\leq \sum_{n\in A_{\{\alpha\}}}\left[\sum_{m\in[\tilde{f}(n),\tilde{f}(n+1))} \frac{1}{2^n n^2}\right]\\ & = \sum_{n\in A_{\{\alpha\}}}\frac{n^2}{2^n n^2}\leq \sum_{n\in A_{\{\alpha\}}}\frac{1}{2^n}\leq 1. \end{align*} $$
$$ \begin{align*} \sum_{n\in B_{\{\alpha\}}} g_{\alpha}(n)&=\sum_{n\in A_{\{\alpha\}}} \left[\sum_{m\in[\tilde{f}(n),\tilde{f}(n+1))}g_{\alpha}(m)\right]\\ &\leq \sum_{n\in A_{\{\alpha\}}}\left[\sum_{m\in[\tilde{f}(n),\tilde{f}(n+1))} \frac{1}{2^n n^2}\right]\\ & = \sum_{n\in A_{\{\alpha\}}}\frac{n^2}{2^n n^2}\leq \sum_{n\in A_{\{\alpha\}}}\frac{1}{2^n}\leq 1. \end{align*} $$
What remains is to find a tall summable ideal
![]() $\mathscr {I}$
which has empty intersection with some ultrafilter extending
$\mathscr {I}$
which has empty intersection with some ultrafilter extending
![]() $\mathcal G$
. Consider the following function from
$\mathcal G$
. Consider the following function from
![]() $\omega $
to
$\omega $
to
![]() $\mathbb {R}$
:
$\mathbb {R}$
:
 $$ \begin{align*} h(n)=\begin{cases} 1, \quad \text{if } n\in [0,\tilde{f}(0)),\\ \frac{1}{k+1}, \quad \text{if } n\in [\tilde{f}(k),\tilde{f}(k+1)). \end{cases} \end{align*} $$
$$ \begin{align*} h(n)=\begin{cases} 1, \quad \text{if } n\in [0,\tilde{f}(0)),\\ \frac{1}{k+1}, \quad \text{if } n\in [\tilde{f}(k),\tilde{f}(k+1)). \end{cases} \end{align*} $$
Let
![]() $\mathscr {I}_{h}$
be the corresponding summable ideal. We claim that
$\mathscr {I}_{h}$
be the corresponding summable ideal. We claim that
![]() $\mathcal {G}\subseteq \mathscr {I}_{h}^{+}$
. Pick any
$\mathcal {G}\subseteq \mathscr {I}_{h}^{+}$
. Pick any
![]() $B_{F}\in \mathcal {G}$
. Then,
$B_{F}\in \mathcal {G}$
. Then,
 $$ \begin{align*} \sum_{n\in B_F} h(n) &= \sum_{n\in A_{F}}\left[\sum_{m\in[\tilde{f}(n),\tilde{f}(n+1))}h(m)\right]\\ & = \sum_{n\in A_{F}}\left[\sum_{m\in[\tilde{f}(n),\tilde{f}(n+1))}\frac{1}{n+1}\right]\\ & = \sum_{n\in A_{F}}\frac{n^2}{n+1}\longrightarrow\infty. \end{align*} $$
$$ \begin{align*} \sum_{n\in B_F} h(n) &= \sum_{n\in A_{F}}\left[\sum_{m\in[\tilde{f}(n),\tilde{f}(n+1))}h(m)\right]\\ & = \sum_{n\in A_{F}}\left[\sum_{m\in[\tilde{f}(n),\tilde{f}(n+1))}\frac{1}{n+1}\right]\\ & = \sum_{n\in A_{F}}\frac{n^2}{n+1}\longrightarrow\infty. \end{align*} $$
Then we have
![]() $\mathcal G\subseteq \mathscr {I}_h^+$
, so
$\mathcal G\subseteq \mathscr {I}_h^+$
, so
![]() $\mathcal {G}\cup \mathscr {I}_h^*$
can be extended to an ultrafilter
$\mathcal {G}\cup \mathscr {I}_h^*$
can be extended to an ultrafilter
![]() $\mathcal U$
. Obviously
$\mathcal U$
. Obviously
![]() $\mathscr {I}_h$
and
$\mathscr {I}_h$
and
![]() $\mathcal U$
satisfy our requirements.
$\mathcal U$
satisfy our requirements.
Now, Theorem 3.1 follows immediately by Theorem 1.2 and Proposition 3.2.
4 Rational Perfect set forcing and p-ideals
Definition 4.1. Let
![]() $\mathscr {I}$
be an ideal on
$\mathscr {I}$
be an ideal on
![]() $\omega $
and let
$\omega $
and let
![]() $\mathcal {U}$
be an ultrafilter on
$\mathcal {U}$
be an ultrafilter on
![]() $\omega $
. We say that
$\omega $
. We say that
![]() $\mathcal {U}$
is an
$\mathcal {U}$
is an
![]() $(\mathscr {I},p)$
-point provided
$(\mathscr {I},p)$
-point provided
![]() $\mathcal {U}$
is an
$\mathcal {U}$
is an
![]() $\mathscr {I}$
-ultrafilter and a p-point at the same time.
$\mathscr {I}$
-ultrafilter and a p-point at the same time.
Remark. One could also define weak
![]() $(\mathscr {I},p)$
-points as those ultrafilters
$(\mathscr {I},p)$
-points as those ultrafilters
![]() $\mathcal {U}$
which are weak
$\mathcal {U}$
which are weak
![]() $\mathscr {I}$
-ultrafilters and p-points. However, it is easy to see that
$\mathscr {I}$
-ultrafilters and p-points. However, it is easy to see that
![]() $(\mathscr {I},p)$
-points and weak
$(\mathscr {I},p)$
-points and weak
![]() $(\mathscr {I},p)$
-points are exactly the same, so for checking that
$(\mathscr {I},p)$
-points are exactly the same, so for checking that
![]() $\mathcal {U}$
is an
$\mathcal {U}$
is an
![]() $(\mathscr {I},p)$
-point we need to check that
$(\mathscr {I},p)$
-point we need to check that
![]() $\mathcal {U}$
is a p-point and a weak
$\mathcal {U}$
is a p-point and a weak
![]() $\mathscr {I}$
-ultrafilter. This remark will be used implicitly in the proofs of Theorems 4.8 and 5.1.
$\mathscr {I}$
-ultrafilter. This remark will be used implicitly in the proofs of Theorems 4.8 and 5.1.
Recall from Section 2, the definition of the Rational Perfect set forcing, denoted by
![]() $\mathbf {PT}$
. Also, recall the definition of the isomorphism
$\mathbf {PT}$
. Also, recall the definition of the isomorphism
![]() $\varphi _T:\omega ^{<\omega }\to split(T)$
. Recall that a forcing
$\varphi _T:\omega ^{<\omega }\to split(T)$
. Recall that a forcing
![]() $\mathbb {P}$
satisfies the Axiom A if there exists a family of orderings
$\mathbb {P}$
satisfies the Axiom A if there exists a family of orderings
![]() $\{\leq _n:n\in \omega \}$
such that:
$\{\leq _n:n\in \omega \}$
such that:
-
(1) For all
 $n\in \omega $
,
$n\in \omega $
,
 $\leq _{n+1}\subseteq \leq _n$
and
$\leq _{n+1}\subseteq \leq _n$
and
 $\leq _0\subseteq \leq $
.
$\leq _0\subseteq \leq $
. -
(2) For any maximal antichain
 $\mathcal {A}$
, any condition
$\mathcal {A}$
, any condition
 $p\in \mathbb {P}$
and any natural number
$p\in \mathbb {P}$
and any natural number
 $n\in \omega $
, there is
$n\in \omega $
, there is
 $q\leq _n p$
such that the set
$q\leq _n p$
such that the set
 $\{a\in \mathcal {A}:a\text { is compatible with }q\}$
is countable.
$\{a\in \mathcal {A}:a\text { is compatible with }q\}$
is countable. -
(3) For any sequence
 $\langle p_n:n\in \omega \rangle $
of condition in
$\langle p_n:n\in \omega \rangle $
of condition in
 $\mathbb {P}$
such that for all
$\mathbb {P}$
such that for all
 $n\in \omega $
it holds that
$n\in \omega $
it holds that
 $p_{n+1}\leq _{n}p_n$
, there is a condition
$p_{n+1}\leq _{n}p_n$
, there is a condition
 $p_{\omega }$
such that for all
$p_{\omega }$
such that for all
 $n\in \omega $
,
$n\in \omega $
,
 $p_{\omega }\leq _n p_n$
.
$p_{\omega }\leq _n p_n$
.
Definition 4.2. Let
![]() $n\in \omega $
be a natural number, and let
$n\in \omega $
be a natural number, and let
![]() $T,S\in \mathbf {PT}$
be two conditions. We say that
$T,S\in \mathbf {PT}$
be two conditions. We say that
![]() $S\leq _n T$
if and only if:
$S\leq _n T$
if and only if:
-
(1)
 $S\leq T$
.
$S\leq T$
. -
(2)
 $\varphi _S(n^{\leq n})=\varphi _T(n^{\leq n})$
.
$\varphi _S(n^{\leq n})=\varphi _T(n^{\leq n})$
.
The following lemmas are well known properties of the Rational Perfect set forcing. We refer the reader to [Reference Miller13] for details about the proofs.
Lemma 4.3. The orders from Definition 4.2 give an Axiom A structure to the Rational Perfect set forcing. In particular,
![]() $\mathbf {PT}$
is proper.
$\mathbf {PT}$
is proper.
Lemma 4.4. Let
![]() $\dot {f}$
be an
$\dot {f}$
be an
![]() $\mathbf {PT}$
-name for a function from
$\mathbf {PT}$
-name for a function from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
,
$\omega $
,
![]() $T\in \mathbf {PT}$
a condition and
$T\in \mathbf {PT}$
a condition and
![]() $g\in \omega ^{\omega }$
such that
$g\in \omega ^{\omega }$
such that
![]() $T\Vdash ` `\dot {f}\leq g"$
. Then there is
$T\Vdash ` `\dot {f}\leq g"$
. Then there is
![]() $T'\leq T$
, and a family
$T'\leq T$
, and a family
![]() $\{h_s:s\in split(T')\}\subseteq \omega ^{\omega }$
such that for all
$\{h_s:s\in split(T')\}\subseteq \omega ^{\omega }$
such that for all
![]() $s\in split(T')$
, for all
$s\in split(T')$
, for all
![]() $n\in \omega $
there is
$n\in \omega $
there is
![]() $k_n\in \omega $
such that for all
$k_n\in \omega $
such that for all
![]() $k\in succ_T(s)$
such that
$k\in succ_T(s)$
such that
![]() $k\ge k_n$
, it holds that
$k\ge k_n$
, it holds that
![]() $T'\upharpoonright s^{\frown } k\Vdash ` `\dot {f}\upharpoonright (\vert s\vert +n)=h_s\upharpoonright (\vert s\vert +n)"$
.
$T'\upharpoonright s^{\frown } k\Vdash ` `\dot {f}\upharpoonright (\vert s\vert +n)=h_s\upharpoonright (\vert s\vert +n)"$
.
Lemma 4.5. Let
![]() $T\in \mathbf {PT}$
be a condition, and
$T\in \mathbf {PT}$
be a condition, and
![]() $A, B$
a partition of the splitting nodes of T. There is a stronger condition
$A, B$
a partition of the splitting nodes of T. There is a stronger condition
![]() $T'\leq T$
such that
$T'\leq T$
such that
![]() $split(T')\subseteq A$
or
$split(T')\subseteq A$
or
![]() $split(T')\subseteq B$
.
$split(T')\subseteq B$
.
Theorem 4.6.
![]() $\mathbf {PT}$
preserves p-points.
$\mathbf {PT}$
preserves p-points.
The following lemma will be useful in the proof of Theorem 4.8, since it will allow us to use Lemma 4.4. For
![]() $f,g\in \omega ^{\omega }$
, the notation
$f,g\in \omega ^{\omega }$
, the notation
![]() $f\leq g$
means that for all
$f\leq g$
means that for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $f(n)\leq g(n)$
.
$f(n)\leq g(n)$
.
Lemma 4.7. Let
![]() $\mathscr {I}$
be an analytic p-ideal. Then there exists a function
$\mathscr {I}$
be an analytic p-ideal. Then there exists a function
![]() $g:\omega \to \omega $
such that for any ultrafilter
$g:\omega \to \omega $
such that for any ultrafilter
![]() $\mathcal {U}$
,
$\mathcal {U}$
,
![]() $\mathcal {U}$
is a weak
$\mathcal {U}$
is a weak
![]() $\mathscr {I}$
-ultrafilter if and only if for all finite to one
$\mathscr {I}$
-ultrafilter if and only if for all finite to one
![]() $f\leq g$
there is
$f\leq g$
there is
![]() $A\in \mathcal {U}$
such that
$A\in \mathcal {U}$
such that
![]() $f[A]\in \mathscr {I}$
.
$f[A]\in \mathscr {I}$
.
Proof Let
![]() $\varphi $
be a lscsm such that
$\varphi $
be a lscsm such that
![]() $\mathscr {I}=Exh(\varphi )$
. Note that for any
$\mathscr {I}=Exh(\varphi )$
. Note that for any
![]() $n\in \omega $
there is
$n\in \omega $
there is
![]() $k\in \omega $
such that for all
$k\in \omega $
such that for all
![]() $i\ge k$
,
$i\ge k$
,
![]() $\varphi (\{i\})\leq \frac {1}{2^n}$
(recall that
$\varphi (\{i\})\leq \frac {1}{2^n}$
(recall that
![]() $\mathscr {I}$
is a tall ideal). Recursively construct a sequence
$\mathscr {I}$
is a tall ideal). Recursively construct a sequence
![]() $\langle k_n:n\in \omega \rangle $
such that for all
$\langle k_n:n\in \omega \rangle $
such that for all
![]() $i\ge k_n$
,
$i\ge k_n$
,
![]() $\varphi (\{i\})\leq \frac {1}{2^n},$
and
$\varphi (\{i\})\leq \frac {1}{2^n},$
and
![]() $k_n<k_{n+1}$
. Then define
$k_n<k_{n+1}$
. Then define
![]() $g_{\varphi }(n)=k_n$
. Let us see that
$g_{\varphi }(n)=k_n$
. Let us see that
![]() $g_{\varphi }$
is a witness for the lemma. It is clear that if
$g_{\varphi }$
is a witness for the lemma. It is clear that if
![]() $\mathcal {U}$
is a weak
$\mathcal {U}$
is a weak
![]() $\mathscr {I}$
-ultrafilter, then for all finite to one
$\mathscr {I}$
-ultrafilter, then for all finite to one
![]() $f:\omega \to \omega $
such that
$f:\omega \to \omega $
such that
![]() $f\leq g_{\varphi }$
there is
$f\leq g_{\varphi }$
there is
![]() $A\in \mathcal {U}$
such that
$A\in \mathcal {U}$
such that
![]() $f[A]\in \mathscr {I}$
. So let us assume that for all finite to one
$f[A]\in \mathscr {I}$
. So let us assume that for all finite to one
![]() $f\leq g_{\varphi }$
there is
$f\leq g_{\varphi }$
there is
![]() $A\in \mathcal {U}$
such that
$A\in \mathcal {U}$
such that
![]() $f[A]\in \mathscr {I}$
. Let
$f[A]\in \mathscr {I}$
. Let
![]() $f\in \omega ^{\omega }$
be an arbitrary finite to one function. If
$f\in \omega ^{\omega }$
be an arbitrary finite to one function. If
![]() $D=\{i\in \omega :{g}_{\varphi }(i)\leq f(i)\}\in \mathcal {U}$
, note that for any
$D=\{i\in \omega :{g}_{\varphi }(i)\leq f(i)\}\in \mathcal {U}$
, note that for any
![]() $i\in D$
,
$i\in D$
,
![]() $\varphi (\{f(i)\})\leq 1/2^i$
, so for any
$\varphi (\{f(i)\})\leq 1/2^i$
, so for any
![]() $n\in \omega $
,
$n\in \omega $
,
 $$ \begin{align*} \varphi(f[D]\cap n)\leq \sum_{j\in f[D]\cap n}\varphi(\{j\})&\leq \\ &\quad \sum_{i\in D,f(i)<n}\varphi(\{f(i)\})\leq\sum_{i\in D,f(i)<n}\frac{1}{2^i}\leq \sum_{i\in D}\frac{1}{2^i}. \end{align*} $$
$$ \begin{align*} \varphi(f[D]\cap n)\leq \sum_{j\in f[D]\cap n}\varphi(\{j\})&\leq \\ &\quad \sum_{i\in D,f(i)<n}\varphi(\{f(i)\})\leq\sum_{i\in D,f(i)<n}\frac{1}{2^i}\leq \sum_{i\in D}\frac{1}{2^i}. \end{align*} $$
Then, by the lower semicontinuity of
![]() $\varphi $
, it follows that
$\varphi $
, it follows that
![]() $\varphi (f[D])\leq \sum _{i\in D}\frac {1}{2^i}$
. This same argument can be used to proved that
$\varphi (f[D])\leq \sum _{i\in D}\frac {1}{2^i}$
. This same argument can be used to proved that
![]() $\varphi (f[D]\setminus n)\leq \sum _{i\in D,f(i)\ge n}\frac {1}{2^i}$
, which implies
$\varphi (f[D]\setminus n)\leq \sum _{i\in D,f(i)\ge n}\frac {1}{2^i}$
, which implies
![]() $\lim _{n\to \infty }\varphi (f[D]\setminus n)=0$
, so
$\lim _{n\to \infty }\varphi (f[D]\setminus n)=0$
, so
![]() $f[D]\in \mathscr {I}$
. On the other hand, if
$f[D]\in \mathscr {I}$
. On the other hand, if
![]() $\omega \setminus D=\{n\in \omega :f(n)<g_{\varphi }(n)\}\in \mathcal {U}$
, then there is a finite to one function
$\omega \setminus D=\{n\in \omega :f(n)<g_{\varphi }(n)\}\in \mathcal {U}$
, then there is a finite to one function
![]() $h\in \omega ^{\omega }$
such that
$h\in \omega ^{\omega }$
such that
![]() $h\leq g$
and
$h\leq g$
and
![]() $\omega \setminus D=\{n\in \omega :f(n)=h(n)\}\in \mathcal {U}$
(just define
$\omega \setminus D=\{n\in \omega :f(n)=h(n)\}\in \mathcal {U}$
(just define
![]() $h\upharpoonright (\omega \setminus D)=f\upharpoonright (\omega \setminus D)$
, and extend it to an arbitrary finite to one function h such that
$h\upharpoonright (\omega \setminus D)=f\upharpoonright (\omega \setminus D)$
, and extend it to an arbitrary finite to one function h such that
![]() $h\leq g_{\varphi }$
). By hypothesis, there is
$h\leq g_{\varphi }$
). By hypothesis, there is
![]() $A\in \mathcal {U}$
such that
$A\in \mathcal {U}$
such that
![]() $h[A]\in \mathscr {I}$
. Define
$h[A]\in \mathscr {I}$
. Define
![]() $B=A\cap (\omega \setminus D)$
, then we have
$B=A\cap (\omega \setminus D)$
, then we have
![]() $f[B]=h[B]\in \mathscr {I}$
.
$f[B]=h[B]\in \mathscr {I}$
.
Now we are ready to prove the following theorem.
Theorem 4.8. Let
![]() $\mathscr {I}$
be an analytic p-ideal and
$\mathscr {I}$
be an analytic p-ideal and
![]() $\mathcal {U}$
an
$\mathcal {U}$
an
![]() $(\mathscr {I},p)$
-point. Then in the generic extension by the Rational Perfect set forcing
$(\mathscr {I},p)$
-point. Then in the generic extension by the Rational Perfect set forcing
![]() $\mathcal U$
generates an
$\mathcal U$
generates an
![]() $(\mathscr {I},p)$
-point.
$(\mathscr {I},p)$
-point.
Proof Fix
![]() $\mathcal {U}$
an
$\mathcal {U}$
an
![]() $(\mathscr {I},p)$
-point. Let
$(\mathscr {I},p)$
-point. Let
![]() $\dot {f}$
be a
$\dot {f}$
be a
![]() $\mathbf {PT}$
-name and
$\mathbf {PT}$
-name and
![]() $p\in \mathbf {PT}$
a condition such that
$p\in \mathbf {PT}$
a condition such that
![]() $p\Vdash ` `\dot {f}\in \omega ^{\omega }"$
. By Lemma 4.7, we can assume that
$p\Vdash ` `\dot {f}\in \omega ^{\omega }"$
. By Lemma 4.7, we can assume that
![]() $p\Vdash ` `\dot {f}\leq g_{\varphi }"$
(note that by absoluteness the same
$p\Vdash ` `\dot {f}\leq g_{\varphi }"$
(note that by absoluteness the same
![]() $g_{\varphi }$
from the ground model works in any generic extension), so we are going to prove that in the generic extension, for any
$g_{\varphi }$
from the ground model works in any generic extension), so we are going to prove that in the generic extension, for any
![]() $\dot {f}\leq g_{\varphi }$
there is
$\dot {f}\leq g_{\varphi }$
there is
![]() $A\in \mathcal {U}$
such that
$A\in \mathcal {U}$
such that
![]() $\dot {f}[A]\in \mathscr {I}$
. By Theorem 4.6,
$\dot {f}[A]\in \mathscr {I}$
. By Theorem 4.6,
![]() $\mathcal U$
remains as a p-point in the generic extension, so we can assume that
$\mathcal U$
remains as a p-point in the generic extension, so we can assume that
![]() $p\Vdash ` `\dot {f} \textit {is finite to one}"$
(the case when
$p\Vdash ` `\dot {f} \textit {is finite to one}"$
(the case when
![]() $\dot {f}$
has a restriction on which it is constant follows immediately). By an application of Lemma 4.4, we can assume that for any
$\dot {f}$
has a restriction on which it is constant follows immediately). By an application of Lemma 4.4, we can assume that for any
![]() $s\in split(p)$
there is a function
$s\in split(p)$
there is a function
![]() $h_s\in \omega ^{\omega }$
such that for all
$h_s\in \omega ^{\omega }$
such that for all
![]() $n\in \omega $
and for all but finitely many
$n\in \omega $
and for all but finitely many
![]() $k\in succ_{p}(s)$
,
$k\in succ_{p}(s)$
,
![]() $p\upharpoonright s^{\frown } k\Vdash ` `\dot {f}\upharpoonright (\lvert s\rvert +n)=h_s\upharpoonright (\lvert s\rvert +n)"$
. Since
$p\upharpoonright s^{\frown } k\Vdash ` `\dot {f}\upharpoonright (\lvert s\rvert +n)=h_s\upharpoonright (\lvert s\rvert +n)"$
. Since
![]() $\mathcal U$
is an
$\mathcal U$
is an
![]() $\mathscr {I}$
-ultrafilter, for every
$\mathscr {I}$
-ultrafilter, for every
![]() $s\in split(p)$
we find
$s\in split(p)$
we find
![]() $A_s\in \mathcal U$
such that
$A_s\in \mathcal U$
such that
![]() $h_s[A_s]\in \mathscr {I}$
. Note that
$h_s[A_s]\in \mathscr {I}$
. Note that
![]() $h_s$
is not necessarily a finite to one function, but since
$h_s$
is not necessarily a finite to one function, but since
![]() $\mathcal U$
is a p-point, we can assume that
$\mathcal U$
is a p-point, we can assume that
![]() $h_s\upharpoonright A_s$
is either constant or finite to one. Now, by Lemma 4.5, we can as well assume that the condition p has one of the following properties:
$h_s\upharpoonright A_s$
is either constant or finite to one. Now, by Lemma 4.5, we can as well assume that the condition p has one of the following properties:
-
a) For all
 $s\in split(p)$
the restriction
$s\in split(p)$
the restriction
 $h_s\upharpoonright A_s$
is finite to one.
$h_s\upharpoonright A_s$
is finite to one. -
b) For all
 $s\in split(p)$
the restriction
$s\in split(p)$
the restriction
 $h_s\upharpoonright A_s$
is a constant
$h_s\upharpoonright A_s$
is a constant
 $a_s$
.
$a_s$
.
Let us consider first the case a). Since
![]() $\mathscr {I}$
is a p-ideal and for all
$\mathscr {I}$
is a p-ideal and for all
![]() $s\in split(p)$
we have
$s\in split(p)$
we have
![]() $h_s[A_s]\in \mathscr {I}$
, then there is
$h_s[A_s]\in \mathscr {I}$
, then there is
![]() $Z\in \mathscr {I}$
such that for all
$Z\in \mathscr {I}$
such that for all
![]() $s\in split(p)$
,
$s\in split(p)$
,
![]() $h_s[A_s]\subseteq ^*Z$
. Removing finitely many elements of each
$h_s[A_s]\subseteq ^*Z$
. Removing finitely many elements of each
![]() $A_s$
, we can assume that for all
$A_s$
, we can assume that for all
![]() $s\in split(p)$
we have
$s\in split(p)$
we have
![]() $h_s[A_s]\subseteq Z$
(recall that we are dealing with case a)). Making use of the p-point game we will construct two sequences
$h_s[A_s]\subseteq Z$
(recall that we are dealing with case a)). Making use of the p-point game we will construct two sequences
![]() $\{F_n:n\in \omega \}$
and
$\{F_n:n\in \omega \}$
and
![]() $\{T_n:n\in \omega \}$
such that:
$\{T_n:n\in \omega \}$
such that:
-
(1)
 $T_0\leq _0 p$
.
$T_0\leq _0 p$
. -
(2) For all
 $n\in \omega $
,
$n\in \omega $
,
 $T_{n+1}\Vdash ` `\dot {f}[F_n]\subseteq Z"$
, and
$T_{n+1}\Vdash ` `\dot {f}[F_n]\subseteq Z"$
, and
 $T_{n+1}\leq _{n+1}T_n$
.
$T_{n+1}\leq _{n+1}T_n$
. -
(3)
 $\bigcup _{n\in \omega } F_n\in \mathcal {U}$
.
$\bigcup _{n\in \omega } F_n\in \mathcal {U}$
. -
(4)
 $T_{\omega }=\bigcap _{n\in \omega } T_n$
is a condition.
$T_{\omega }=\bigcap _{n\in \omega } T_n$
is a condition.
The construction is as follows:
-
(i) Player I starts playing
 $A_0=A_{st(p)}$
, and define
$A_0=A_{st(p)}$
, and define
 $T_0=p$
.
$T_0=p$
. -
(ii) Suppose Player II has answered with a set
 $F_0\subseteq A_0$
. Let
$F_0\subseteq A_0$
. Let
 $k_0\in \omega $
be big enough so that for all
$k_0\in \omega $
be big enough so that for all
 $i\in succ_{T_0}(st(T_0))\setminus k_0$
it holds that
$i\in succ_{T_0}(st(T_0))\setminus k_0$
it holds that
 $T\upharpoonright st(T_0)^{\frown } i\Vdash ` `\dot {f}\upharpoonright (\max (F_0)+1)=h_{st(T_0)}\upharpoonright (\max (F_0)+1)$
”. Note that this implies that for all
$T\upharpoonright st(T_0)^{\frown } i\Vdash ` `\dot {f}\upharpoonright (\max (F_0)+1)=h_{st(T_0)}\upharpoonright (\max (F_0)+1)$
”. Note that this implies that for all
 $i\ge k_0$
,
$i\ge k_0$
,
 $T_0\upharpoonright st(T_0)^{\frown } i\Vdash ` `\dot {f}[F_0]\subseteq Z"$
. Then define
$T_0\upharpoonright st(T_0)^{\frown } i\Vdash ` `\dot {f}[F_0]\subseteq Z"$
. Then define  $$ \begin{align*} T_1=\bigcup_{\substack{i\ge k_0,\\ i\in succ_{T_0}(st(T_0))}}T_0\upharpoonright st(T_0)^{\frown} i. \end{align*} $$
$$ \begin{align*} T_1=\bigcup_{\substack{i\ge k_0,\\ i\in succ_{T_0}(st(T_0))}}T_0\upharpoonright st(T_0)^{\frown} i. \end{align*} $$
Then Player I plays the set
 $A_1=\bigcap _{s\in {1^{\leq 1}}}A_{\varphi _{T_1}(s)}\setminus (\max (F_0)+1)$
.
$A_1=\bigcap _{s\in {1^{\leq 1}}}A_{\varphi _{T_1}(s)}\setminus (\max (F_0)+1)$
. -
(iii) Suppose at round number n Player I has played the set
 $$ \begin{align*} A_n=\bigcap_{s\in n^{\leq n}} A_{\varphi_{T_n}(s)}\setminus \left(\max\left(\bigcup_{k<n}F_k\right)+1\right). \end{align*} $$
$$ \begin{align*} A_n=\bigcap_{s\in n^{\leq n}} A_{\varphi_{T_n}(s)}\setminus \left(\max\left(\bigcup_{k<n}F_k\right)+1\right). \end{align*} $$
Suppose Player II responds with a finite set
 $F_n\subseteq A_n$
. Then, let
$F_n\subseteq A_n$
. Then, let
 $k_n\in \omega $
be big enough such that for all
$k_n\in \omega $
be big enough such that for all
 $r\in \varphi _{T_n}(n^{\leq n})$
and all
$r\in \varphi _{T_n}(n^{\leq n})$
and all
 $i\in succ_{T_n}(r)\setminus k_n$
, it holds that
$i\in succ_{T_n}(r)\setminus k_n$
, it holds that
 $T_n\upharpoonright r^{\frown } i\Vdash ` `\dot {f}\upharpoonright (\max \left (\bigcup _{k\leq n}F_n\right )+1)=h_{r}\upharpoonright (\max \left (\bigcup _{k\leq n}F_n\right )+1)"$
. Note that this implies that for each
$T_n\upharpoonright r^{\frown } i\Vdash ` `\dot {f}\upharpoonright (\max \left (\bigcup _{k\leq n}F_n\right )+1)=h_{r}\upharpoonright (\max \left (\bigcup _{k\leq n}F_n\right )+1)"$
. Note that this implies that for each
 $r\in \varphi _{T_n}(n^{\leq n})$
and
$r\in \varphi _{T_n}(n^{\leq n})$
and
 $i\in succ_{T_n}(r)\setminus k_n$
,
$i\in succ_{T_n}(r)\setminus k_n$
,
 $T_n\upharpoonright r^{\frown } i\Vdash ` `\dot {f}[F_n]\subseteq Z"$
. Then define
$T_n\upharpoonright r^{\frown } i\Vdash ` `\dot {f}[F_n]\subseteq Z"$
. Then define
 $T_{n+1}$
as follows:
$T_{n+1}$
as follows:  $$ \begin{align*} T_{n+1}=\bigcup_{s\in n^{\leq n}}\bigcup_{\substack{i\ge k_n,\\ i\in succ_{T_n}(\varphi_{T_n}(s))}}T\upharpoonright \varphi_{T_n}(s)^{\frown} i. \end{align*} $$
$$ \begin{align*} T_{n+1}=\bigcup_{s\in n^{\leq n}}\bigcup_{\substack{i\ge k_n,\\ i\in succ_{T_n}(\varphi_{T_n}(s))}}T\upharpoonright \varphi_{T_n}(s)^{\frown} i. \end{align*} $$
By construction it follows that
 $T_{n+1}\Vdash ` `\dot {f}[F_n]\subseteq Z"$
. Let Player I play the set
$T_{n+1}\Vdash ` `\dot {f}[F_n]\subseteq Z"$
. Let Player I play the set  $$ \begin{align*} A_{n+1}=\bigcap_{s\in(n+1)^{\leq n+1}} A_{\varphi_{T_{n+1}}(s)}\setminus\left(\max\left(\bigcup_{k\leq n}F_k\right)+1 \right). \end{align*} $$
$$ \begin{align*} A_{n+1}=\bigcap_{s\in(n+1)^{\leq n+1}} A_{\varphi_{T_{n+1}}(s)}\setminus\left(\max\left(\bigcup_{k\leq n}F_k\right)+1 \right). \end{align*} $$
By Lemma 2.2, this is not a winning strategy for Player I, so there is a play where Player II wins the game. Let
![]() $\{F_n:n\in \omega \}$
and
$\{F_n:n\in \omega \}$
and
![]() $\{T_n:n\in \omega \}$
be the sequences constructed by Player I in this play, and define
$\{T_n:n\in \omega \}$
be the sequences constructed by Player I in this play, and define
![]() $T_{\omega }=\bigcap _{n\in \omega }T_n$
.
$T_{\omega }=\bigcap _{n\in \omega }T_n$
.
Claim.
![]() $T_{\omega }\Vdash ` `\dot {f}[\bigcup _{n\in \omega }F_n]\subseteq Z"$
. As pointed out in the construction of the two sequences, it holds that
$T_{\omega }\Vdash ` `\dot {f}[\bigcup _{n\in \omega }F_n]\subseteq Z"$
. As pointed out in the construction of the two sequences, it holds that
![]() $T_{n+1}\Vdash ` `\dot {f}[F_n]\subseteq Z"$
. But for all n,
$T_{n+1}\Vdash ` `\dot {f}[F_n]\subseteq Z"$
. But for all n,
![]() $T_{\omega }\leq T_n$
, so the claim is true for
$T_{\omega }\leq T_n$
, so the claim is true for
![]() $T_{\omega }$
.
$T_{\omega }$
.
Now let us deal with case b). Fist note that there is no condition
![]() $q\leq p$
such that the set
$q\leq p$
such that the set
![]() $\{a_s:s\in splitt(q)\}$
is finite. To prove this assume it is false and apply Lemma 4.5 finitely many times, then recall that the function
$\{a_s:s\in splitt(q)\}$
is finite. To prove this assume it is false and apply Lemma 4.5 finitely many times, then recall that the function
![]() $\dot {f}$
is a finite to one function to arrive at a contradiction. By using this remark it is possible to find a stronger condition
$\dot {f}$
is a finite to one function to arrive at a contradiction. By using this remark it is possible to find a stronger condition
![]() $q\leq p$
such that
$q\leq p$
such that
![]() $Z=\{a_s:s\in split(q)\}\in \mathscr {I}$
. The rest follows the same lines of the previous case. Using the p-point game again we construct two sequences
$Z=\{a_s:s\in split(q)\}\in \mathscr {I}$
. The rest follows the same lines of the previous case. Using the p-point game again we construct two sequences
![]() $\{F_n:n\in \omega \}$
and
$\{F_n:n\in \omega \}$
and
![]() $\{T_n:n\in \omega \}$
such that conditions (2)–(5) of the construction for case a) hold, and condition (1) is changed to (1’)
$\{T_n:n\in \omega \}$
such that conditions (2)–(5) of the construction for case a) hold, and condition (1) is changed to (1’)
![]() $T_0\leq q$
. The strategy for player I is defined in the same way as it was in the previous case. Then the condition
$T_0\leq q$
. The strategy for player I is defined in the same way as it was in the previous case. Then the condition
![]() $T_{\omega }$
and the set
$T_{\omega }$
and the set
![]() $\bigcup _{n\in \omega }F_n$
constructed in this way satisfy
$\bigcup _{n\in \omega }F_n$
constructed in this way satisfy
![]() $T\Vdash ` `\dot {f}[\bigcup _{n\in \omega }F_n]\subseteq Z"$
.
$T\Vdash ` `\dot {f}[\bigcup _{n\in \omega }F_n]\subseteq Z"$
.
5 A preservation theorem for
 $(\mathscr {I},p)$
-points
$(\mathscr {I},p)$
-points
In this section we prove the following preservation theorem for
![]() $(\mathscr {I},p)$
-points. We say that a forcing
$(\mathscr {I},p)$
-points. We say that a forcing
![]() $\mathbb {P}$
preserves
$\mathbb {P}$
preserves
![]() $(\mathscr {I},p)$
-points if any
$(\mathscr {I},p)$
-points if any
![]() $(\mathscr {I},p)$
-point from the ground model generates an
$(\mathscr {I},p)$
-point from the ground model generates an
![]() $(\mathscr {I},p)$
-point after forcing with
$(\mathscr {I},p)$
-point after forcing with
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Theorem 5.1. Let
![]() $\mathscr {I}$
be an analytic p-ideal such that
$\mathscr {I}$
be an analytic p-ideal such that
![]() $\mathscr {I}=Fin(\varphi )=Exh(\varphi )$
, for some lscsm
$\mathscr {I}=Fin(\varphi )=Exh(\varphi )$
, for some lscsm
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $\langle \mathbb {P}_{\beta },\dot {\mathbb {Q}}_{\beta }:\beta <\alpha \rangle $
be a countable support iteration of proper forcing notions such that for all
$\langle \mathbb {P}_{\beta },\dot {\mathbb {Q}}_{\beta }:\beta <\alpha \rangle $
be a countable support iteration of proper forcing notions such that for all
![]() $\beta <\alpha $
,
$\beta <\alpha $
,
![]() $\mathbb {P}_{\beta }$
is proper, preserves
$\mathbb {P}_{\beta }$
is proper, preserves
![]() $(\mathscr {I},p)$
-points and
$(\mathscr {I},p)$
-points and
![]() $\mathbb {P}_{\beta }\Vdash ` `\dot {\mathbb {Q}}_{\beta } \textit { is proper and preserves }(\mathscr {I},p)\textit {-points}"$
. Then
$\mathbb {P}_{\beta }\Vdash ` `\dot {\mathbb {Q}}_{\beta } \textit { is proper and preserves }(\mathscr {I},p)\textit {-points}"$
. Then
![]() $\mathbb {P}_{\alpha }$
preserves
$\mathbb {P}_{\alpha }$
preserves
![]() $(\mathscr {I},p)$
-points.
$(\mathscr {I},p)$
-points.
Recall that given a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {f}$
for a real, a pair
$\dot {f}$
for a real, a pair
![]() $(\langle p_n:n\in \omega \rangle ,h)$
is an interpretation for
$(\langle p_n:n\in \omega \rangle ,h)$
is an interpretation for
![]() $\dot {f}$
if
$\dot {f}$
if
![]() $\langle p_n:n\in \omega \rangle $
is a decreasing sequence and for all
$\langle p_n:n\in \omega \rangle $
is a decreasing sequence and for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $p_n\Vdash ` `\dot {f}\upharpoonright n=h\upharpoonright n"$
. In such case, we say that
$p_n\Vdash ` `\dot {f}\upharpoonright n=h\upharpoonright n"$
. In such case, we say that
![]() $\langle p_n:n\in \omega \rangle $
interprets
$\langle p_n:n\in \omega \rangle $
interprets
![]() $\dot {f}$
as h. We need a strengthening of this property.
$\dot {f}$
as h. We need a strengthening of this property.
Definition 5.2. Let
![]() $\dot {f}$
be a
$\dot {f}$
be a
![]() $\mathbb P$
-name for a finite to one function from
$\mathbb P$
-name for a finite to one function from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
and
$\omega $
and
![]() $p\in \mathbb {P}$
a condition. A fine interpretation for
$p\in \mathbb {P}$
a condition. A fine interpretation for
![]() $\dot f$
below p is a pair
$\dot f$
below p is a pair
![]() $(\langle p_n:n\in \omega \rangle ,h)$
such that
$(\langle p_n:n\in \omega \rangle ,h)$
such that
![]() $\langle p_n:n\in \omega \rangle $
is a decreasing sequence,
$\langle p_n:n\in \omega \rangle $
is a decreasing sequence,
![]() $p_0\leq p$
, h is a finite to one function and for all
$p_0\leq p$
, h is a finite to one function and for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $p_n\Vdash ` `\dot {f}\upharpoonright n=h\upharpoonright n"$
and
$p_n\Vdash ` `\dot {f}\upharpoonright n=h\upharpoonright n"$
and
![]() $p_n$
decides the value of
$p_n$
decides the value of
![]() $\dot {f}^{-1}(n)$
.
$\dot {f}^{-1}(n)$
.
It is easy to see that if
![]() $\dot f$
is forced to be a finite to one function, then given a condition p, we can find a fine interpretation for
$\dot f$
is forced to be a finite to one function, then given a condition p, we can find a fine interpretation for
![]() $\dot {f}$
below p. In order to prove Theorem 5.1, we need a slight modification of the notion of derived sequence defined in [Reference Abraham, Foreman and Kanamori1]. There are many different ways to proceed, but we choose to recall the usual notion of derived sequence, and then make use of Lemma 5.4 to state the existence of the objects we need. The notion we work with is that of fine derived sequence, and it is stated just before Lemma 5.4. Alternatively, it is possible to state everything we need in only one definition.
$\dot {f}$
below p. In order to prove Theorem 5.1, we need a slight modification of the notion of derived sequence defined in [Reference Abraham, Foreman and Kanamori1]. There are many different ways to proceed, but we choose to recall the usual notion of derived sequence, and then make use of Lemma 5.4 to state the existence of the objects we need. The notion we work with is that of fine derived sequence, and it is stated just before Lemma 5.4. Alternatively, it is possible to state everything we need in only one definition.
Definition 5.3. Let
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
be a two step forcing iteration, and let
$\mathbb {P}*\dot {\mathbb {Q}}$
be a two step forcing iteration, and let
![]() $\dot {f}$
be a
$\dot {f}$
be a
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
-name and
$\mathbb {P}*\dot {\mathbb {Q}}$
-name and
![]() $(p,\dot {q})\in \mathbb {P}*\dot {\mathbb {Q}}$
a condition such that
$(p,\dot {q})\in \mathbb {P}*\dot {\mathbb {Q}}$
a condition such that
![]() $(p,\dot {q})\Vdash ` `\dot {f}\in \omega ^{\omega }"$
. Let
$(p,\dot {q})\Vdash ` `\dot {f}\in \omega ^{\omega }"$
. Let
![]() $\sqsubseteq $
be a well ordering of
$\sqsubseteq $
be a well ordering of
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
. Let
$\mathbb {P}*\dot {\mathbb {Q}}$
. Let
![]() $(\langle r_n:n\in \omega \rangle ,h)$
be an interpretation of
$(\langle r_n:n\in \omega \rangle ,h)$
be an interpretation of
![]() $\dot {f}$
below
$\dot {f}$
below
![]() $(p,\dot {q})$
, where
$(p,\dot {q})$
, where
![]() $r_n=(p_n,\dot {q}_n)$
. Suppose
$r_n=(p_n,\dot {q}_n)$
. Suppose
![]() $G_{\mathbb {P}}$
is a generic filter for
$G_{\mathbb {P}}$
is a generic filter for
![]() $\mathbb {P}$
over V. Then, in
$\mathbb {P}$
over V. Then, in
![]() $V[G_{\mathbb {P}}]$
, define the following decreasing sequence of conditions
$V[G_{\mathbb {P}}]$
, define the following decreasing sequence of conditions
![]() $\langle t_n:n\in \omega \rangle $
in
$\langle t_n:n\in \omega \rangle $
in
![]() $\dot {\mathbb {Q}}[G_{\mathbb {P}}]$
which interprets
$\dot {\mathbb {Q}}[G_{\mathbb {P}}]$
which interprets
![]() $\dot {f}$
:
$\dot {f}$
:
-
(1) Define
 $n^*=\sup (\{n\in \{-1\}\cup \omega :p_n\in G_{\mathbb {P}}\})$
, where
$n^*=\sup (\{n\in \{-1\}\cup \omega :p_n\in G_{\mathbb {P}}\})$
, where
 $r_{-1}=(p_{-1},\dot {q}_{-1})=(1_{\mathbb {P}},1_{\dot {\mathbb {Q}}})$
.
$r_{-1}=(p_{-1},\dot {q}_{-1})=(1_{\mathbb {P}},1_{\dot {\mathbb {Q}}})$
. -
(2) For
 $n\in \{-1\}\cup \omega $
, if
$n\in \{-1\}\cup \omega $
, if
 $n\leq n^*$
, define
$n\leq n^*$
, define
 $t_n=\dot {q}_n[{G}_{\mathbb {P}}]$
.
$t_n=\dot {q}_n[{G}_{\mathbb {P}}]$
. -
(3) For
 $n\in \omega $
, if
$n\in \omega $
, if
 $n>n^*$
, then define
$n>n^*$
, then define
 $t_n$
to be
$t_n$
to be
 $\dot {s}_n[G_{\mathbb {P}}]$
, where
$\dot {s}_n[G_{\mathbb {P}}]$
, where
 $\dot {s}_n$
is such that there is
$\dot {s}_n$
is such that there is
 $u_n\in \mathbb {P}$
such that
$u_n\in \mathbb {P}$
such that
 $(u_n,\dot {s}_n)\in \mathbb {P}*\dot {\mathbb {Q}}$
is an extension of
$(u_n,\dot {s}_n)\in \mathbb {P}*\dot {\mathbb {Q}}$
is an extension of
 $(u_{n-1},\dot {s}_{n-1})$
such that
$(u_{n-1},\dot {s}_{n-1})$
such that
 $u_{n}\in G_{\mathbb {P}}$
and
$u_{n}\in G_{\mathbb {P}}$
and
 $\dot {s}_n[G_{\mathbb {P}}]$
decides the value of
$\dot {s}_n[G_{\mathbb {P}}]$
decides the value of
 $\dot {f}\upharpoonright n$
, and
$\dot {f}\upharpoonright n$
, and
 $(u_n,\dot {s}_n)$
is
$(u_n,\dot {s}_n)$
is
 $\sqsubseteq $
-minimal with this property.
$\sqsubseteq $
-minimal with this property.
The sequence
![]() $\langle t_i:i\in \omega \rangle $
defined in
$\langle t_i:i\in \omega \rangle $
defined in
![]() $V[G_{\mathbb {P}}]$
is said to be the derived sequence from
$V[G_{\mathbb {P}}]$
is said to be the derived sequence from
![]() $\langle r_n:n\in \omega \rangle $
,
$\langle r_n:n\in \omega \rangle $
,
![]() $G_{\mathbb {P}}$
,
$G_{\mathbb {P}}$
,
![]() $\sqsubseteq $
and
$\sqsubseteq $
and
![]() $\dot {f}$
, and we write
$\dot {f}$
, and we write
![]() $\delta _{G_{\mathbb {P}}}(\langle r_n:n\in \omega \rangle ,\dot {f})$
to denote this sequence, and a
$\delta _{G_{\mathbb {P}}}(\langle r_n:n\in \omega \rangle ,\dot {f})$
to denote this sequence, and a
![]() $\mathbb {P}$
-name of this sequence will be denoted by
$\mathbb {P}$
-name of this sequence will be denoted by
![]() $\tilde {\delta }(\langle r_n:n\in \omega \rangle ,\dot {f})$
. Note that by clause (3), in
$\tilde {\delta }(\langle r_n:n\in \omega \rangle ,\dot {f})$
. Note that by clause (3), in
![]() $V[G_{\mathbb {P}}]$
there is a function g such that
$V[G_{\mathbb {P}}]$
there is a function g such that
![]() $\delta _{G_{\mathbb {P}}}(\langle r_n:n\in \omega \rangle ,\dot {f})$
interprets
$\delta _{G_{\mathbb {P}}}(\langle r_n:n\in \omega \rangle ,\dot {f})$
interprets
![]() $\dot {f}$
as g. If
$\dot {f}$
as g. If
![]() $\tilde {\delta }(\langle r_n:n\in \omega \rangle ,\dot {f})$
is the
$\tilde {\delta }(\langle r_n:n\in \omega \rangle ,\dot {f})$
is the
![]() $\mathbb {P}$
-name for the derived sequence in
$\mathbb {P}$
-name for the derived sequence in
![]() $V[G_{\mathbb {P}}]$
, then define
$V[G_{\mathbb {P}}]$
, then define
![]() $\textrm{int}(\tilde {\delta }(\langle r_n:n\in \omega \rangle ,\dot {f}),\dot {f})$
to be a
$\textrm{int}(\tilde {\delta }(\langle r_n:n\in \omega \rangle ,\dot {f}),\dot {f})$
to be a
![]() $\mathbb {P}$
-name for the function g such that in
$\mathbb {P}$
-name for the function g such that in
![]() $V[G_{\mathbb {P}}]$
, the pair
$V[G_{\mathbb {P}}]$
, the pair
![]() $(\delta _{G_{\mathbb {P}}}(\langle r_n:n\in \omega \rangle ,\dot {f}),\dot {g})$
is an interpretation of
$(\delta _{G_{\mathbb {P}}}(\langle r_n:n\in \omega \rangle ,\dot {f}),\dot {g})$
is an interpretation of
![]() $\dot {f}$
.
$\dot {f}$
.
It is easy to see that if
![]() $\dot {g}=\textrm{int}(\tilde {\delta }(\bar {r},\dot {f}),\dot {f})$
, and
$\dot {g}=\textrm{int}(\tilde {\delta }(\bar {r},\dot {f}),\dot {f})$
, and
![]() $\bar {r}$
interprets
$\bar {r}$
interprets
![]() $\dot {f}$
as h, then
$\dot {f}$
as h, then
![]() $\bar {p}$
interprets
$\bar {p}$
interprets
![]() $\dot {g}$
as h. Also note that clause (3) of the previous definition allows some flexibility in the choice of
$\dot {g}$
as h. Also note that clause (3) of the previous definition allows some flexibility in the choice of
![]() $t_n$
, so we can add more requirements to be satisfied by
$t_n$
, so we can add more requirements to be satisfied by
![]() $t_n$
in relation to
$t_n$
in relation to
![]() $\dot {f}$
. This is where our modification takes place: if
$\dot {f}$
. This is where our modification takes place: if
![]() $\dot {f}$
is forced to be a finite to one function, we could additionally required in clause (3) that
$\dot {f}$
is forced to be a finite to one function, we could additionally required in clause (3) that
![]() $t_n$
determines not only the initial segment
$t_n$
determines not only the initial segment
![]() $\dot {f}\upharpoonright n$
, but also
$\dot {f}\upharpoonright n$
, but also
![]() $\dot {f}^{-1}(n)$
. In this way,
$\dot {f}^{-1}(n)$
. In this way,
![]() $\dot {g}=\textrm{int}(\tilde {\delta }(\bar {r},\dot {f}),\dot {f})$
is forced to be finite to one. Derived sequences having this property will be called fine derived sequences. This is the notion we work with in Lemma 5.4 and the proof of Theorem 5.1. On the other hand, strictly speaking, the derived sequence
$\dot {g}=\textrm{int}(\tilde {\delta }(\bar {r},\dot {f}),\dot {f})$
is forced to be finite to one. Derived sequences having this property will be called fine derived sequences. This is the notion we work with in Lemma 5.4 and the proof of Theorem 5.1. On the other hand, strictly speaking, the derived sequence
![]() $\tilde {\delta }(\langle r_n:n\in \omega \rangle ,\dot {f})$
and the
$\tilde {\delta }(\langle r_n:n\in \omega \rangle ,\dot {f})$
and the
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\textrm{int}(\tilde {\delta }(\bar {r},\dot {f}),\dot {f})$
depend not only on
$\textrm{int}(\tilde {\delta }(\bar {r},\dot {f}),\dot {f})$
depend not only on
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
,
$\mathbb {P}*\dot {\mathbb {Q}}$
,
![]() $\dot {f}$
,
$\dot {f}$
,
![]() $\langle r_n:n\in \omega \rangle $
and G, but also on
$\langle r_n:n\in \omega \rangle $
and G, but also on
![]() $\sqsubseteq $
, and is uniquely determined by this five parameters. With exception of Lemma 5.4, we will usually not explicitly mention the well ordering
$\sqsubseteq $
, and is uniquely determined by this five parameters. With exception of Lemma 5.4, we will usually not explicitly mention the well ordering
![]() $\sqsubseteq $
, and when we mention the expressions a derived sequence or a fine derived sequence, we assume that a well ordering
$\sqsubseteq $
, and when we mention the expressions a derived sequence or a fine derived sequence, we assume that a well ordering
![]() $\sqsubseteq $
of the forcing has been fixed for the whole proof, and implicitly assume that the (fine)derived sequence at hand depends on such well ordering.
$\sqsubseteq $
of the forcing has been fixed for the whole proof, and implicitly assume that the (fine)derived sequence at hand depends on such well ordering.
Lemma 5.4. Let
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
be a forcing iteration,
$\mathbb {P}*\dot {\mathbb {Q}}$
be a forcing iteration,
![]() $\dot f$
a
$\dot f$
a
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
-name for a finite to one function, and
$\mathbb {P}*\dot {\mathbb {Q}}$
-name for a finite to one function, and
![]() $(p,\dot {q})\in \mathbb {P}*\dot {\mathbb {Q}}$
a condition. Let
$(p,\dot {q})\in \mathbb {P}*\dot {\mathbb {Q}}$
a condition. Let
![]() $(\langle r_n:n\in \omega \rangle ,h)$
be a fine interpretation for
$(\langle r_n:n\in \omega \rangle ,h)$
be a fine interpretation for
![]() $\dot f$
below
$\dot f$
below
![]() $(p,\dot {q})$
, where
$(p,\dot {q})$
, where
![]() $r_n=(p_n,\dot {q}_n)$
. Let
$r_n=(p_n,\dot {q}_n)$
. Let
![]() $\sqsubseteq $
be a well ordering of
$\sqsubseteq $
be a well ordering of
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
. Then there is a
$\mathbb {P}*\dot {\mathbb {Q}}$
. Then there is a
![]() $\mathbb {P}$
-name for a fine derived sequence
$\mathbb {P}$
-name for a fine derived sequence
![]() $\tilde {\delta }=\tilde {\delta }(\langle r_n:n\in \omega ,\dot f\rangle )$
, and the pair
$\tilde {\delta }=\tilde {\delta }(\langle r_n:n\in \omega ,\dot f\rangle )$
, and the pair
![]() $(\tilde {\delta },\textrm{int}(\tilde {\delta },\dot {f}))$
is forced to be a fine interpretation of
$(\tilde {\delta },\textrm{int}(\tilde {\delta },\dot {f}))$
is forced to be a fine interpretation of
![]() $\dot f$
in
$\dot f$
in
![]() $V[\dot {G}_{\mathbb P}]$
. Moreover,
$V[\dot {G}_{\mathbb P}]$
. Moreover,
![]() $(\langle p_n:n\in \omega \rangle ,h)$
is a fine interpretation of
$(\langle p_n:n\in \omega \rangle ,h)$
is a fine interpretation of
![]() $\textrm{int}(\tilde {\delta },\dot {f})$
.
$\textrm{int}(\tilde {\delta },\dot {f})$
.
Proof We follow the same notation as in Definition 5.3. Let
![]() $G_{\mathbb {P}}\subseteq \mathbb {P}$
be a generic filter over V, define
$G_{\mathbb {P}}\subseteq \mathbb {P}$
be a generic filter over V, define
![]() $r_{-1}=(p_{-1},\dot {q}_{-1})=(1_{\mathbb {P}},1_{\dot {\mathbb {Q}}})$
and
$r_{-1}=(p_{-1},\dot {q}_{-1})=(1_{\mathbb {P}},1_{\dot {\mathbb {Q}}})$
and
![]() $n^*=\sup (\{n\in \{-1\}\cup \omega :p_n\in G_{\mathbb {P}}\})$
. Define
$n^*=\sup (\{n\in \{-1\}\cup \omega :p_n\in G_{\mathbb {P}}\})$
. Define
![]() $\tilde {\delta }$
as a
$\tilde {\delta }$
as a
![]() $\mathbb {P}$
-name for the sequence
$\mathbb {P}$
-name for the sequence
![]() $\langle t_n:n\in \omega \rangle $
of conditions in
$\langle t_n:n\in \omega \rangle $
of conditions in
![]() $\dot {\mathbb {Q}}[G_{\mathbb {P}}]$
defined as follows:
$\dot {\mathbb {Q}}[G_{\mathbb {P}}]$
defined as follows:
-
For all
 $n\in \omega $
, if
$n\in \omega $
, if
 $n\leq n^*$
, then
$n\leq n^*$
, then
 $t_n=\dot {q}_n[G_{\mathbb {P}}]$
, and for all natural number
$t_n=\dot {q}_n[G_{\mathbb {P}}]$
, and for all natural number
 $n> n^*$
, define
$n> n^*$
, define
 $t_n$
to be
$t_n$
to be
 $\dot {s}_n[G_{\mathbb {P}}]$
, where
$\dot {s}_n[G_{\mathbb {P}}]$
, where
 $\dot {s}_n$
is such that there is
$\dot {s}_n$
is such that there is
 $u_n\in \mathbb {P}$
such that
$u_n\in \mathbb {P}$
such that
 $(u_n,\dot {s}_n)\in \mathbb {P}*\dot {\mathbb {Q}}$
is the
$(u_n,\dot {s}_n)\in \mathbb {P}*\dot {\mathbb {Q}}$
is the
 $\sqsubseteq $
-first extension of
$\sqsubseteq $
-first extension of
 $(u_{n-1},\dot {s}_{n-1})$
such that
$(u_{n-1},\dot {s}_{n-1})$
such that
 $u_n\in G_{\mathbb {P}}$
, and
$u_n\in G_{\mathbb {P}}$
, and
 $\dot {s}_n[G_{\mathbb {P}}]$
decides the value of
$\dot {s}_n[G_{\mathbb {P}}]$
decides the value of
 $\dot {f}^{-1}(n)$
and
$\dot {f}^{-1}(n)$
and
 $\dot {f}\upharpoonright n$
. Let
$\dot {f}\upharpoonright n$
. Let
 $g\in \omega ^{\omega }$
be the function such that
$g\in \omega ^{\omega }$
be the function such that
 $t_n\Vdash ` `\dot {f}\upharpoonright n=g\upharpoonright n"$
. Define
$t_n\Vdash ` `\dot {f}\upharpoonright n=g\upharpoonright n"$
. Define
 $\textrm{int}(\tilde {\delta },\dot {f})$
as a
$\textrm{int}(\tilde {\delta },\dot {f})$
as a
 $\mathbb {P}$
-name for g.
$\mathbb {P}$
-name for g.
By definition of
![]() $\tilde {\delta }$
and the definition of
$\tilde {\delta }$
and the definition of
![]() $\textrm{int}(\tilde {\delta },\dot {f})$
, it follows that
$\textrm{int}(\tilde {\delta },\dot {f})$
, it follows that
![]() $\tilde {\delta }$
is a fine derived sequence and the pair
$\tilde {\delta }$
is a fine derived sequence and the pair
![]() $(\tilde {\delta },\textrm{int}(\tilde {\delta },\dot {f}))$
is forced to a fine interpretation of
$(\tilde {\delta },\textrm{int}(\tilde {\delta },\dot {f}))$
is forced to a fine interpretation of
![]() $\dot {f}$
in
$\dot {f}$
in
![]() $V[\dot {G}_{\mathbb {P}}]$
, since
$V[\dot {G}_{\mathbb {P}}]$
, since
![]() $\textrm{int}(\tilde \delta ,\dot {f})$
is actually a
$\textrm{int}(\tilde \delta ,\dot {f})$
is actually a
![]() $\mathbb {P}$
-name of the function g. It is easy to see that
$\mathbb {P}$
-name of the function g. It is easy to see that
![]() $(\langle p_n:n\in \omega \rangle ,h)$
is a fine interpretation of
$(\langle p_n:n\in \omega \rangle ,h)$
is a fine interpretation of
![]() $\textrm{int}(\tilde {\delta },\dot {f})$
.
$\textrm{int}(\tilde {\delta },\dot {f})$
.
The next lemma can be seen as an intermediate step in the proof of Theorem 5.1, but we consider that it is more readable to write it down as a separated lemma.
Lemma 5.5. Let
![]() $\mathscr {I}$
be an ideal such that
$\mathscr {I}$
be an ideal such that
![]() $\mathscr {I}=Fin(\varphi )=Exh(\varphi )$
, for some lscsm
$\mathscr {I}=Fin(\varphi )=Exh(\varphi )$
, for some lscsm
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $\mathcal {U}$
be an
$\mathcal {U}$
be an
![]() $(\mathscr {I},p)$
-point. Let
$(\mathscr {I},p)$
-point. Let
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
be a two step iteration of proper forcings such that
$\mathbb {P}*\dot {\mathbb {Q}}$
be a two step iteration of proper forcings such that
![]() $\mathbb {P}$
preserves
$\mathbb {P}$
preserves
![]() $(\mathscr {I},p)$
-points. Let
$(\mathscr {I},p)$
-points. Let
![]() $\dot {f}$
be a
$\dot {f}$
be a
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
-name for a finite to one function from
$\mathbb {P}*\dot {\mathbb {Q}}$
-name for a finite to one function from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
. Let
$\omega $
. Let
![]() $(p,\dot {q})\in \mathbb {P}*\dot {\mathbb {Q}}$
be a condition and
$(p,\dot {q})\in \mathbb {P}*\dot {\mathbb {Q}}$
be a condition and
![]() $(\langle r_n:n\in \omega \rangle , h_0)$
be a fine interpretation of
$(\langle r_n:n\in \omega \rangle , h_0)$
be a fine interpretation of
![]() $\dot {f}$
below the condition
$\dot {f}$
below the condition
![]() $(p,\dot {q})$
. We can assume that
$(p,\dot {q})$
. We can assume that
![]() $r_n=(p_n,\dot {q}_n)$
. Let
$r_n=(p_n,\dot {q}_n)$
. Let
![]() $\mathcal {M}\prec H(\theta )$
be a countable elementary submodel such that
$\mathcal {M}\prec H(\theta )$
be a countable elementary submodel such that
![]() $p,\dot {f},\mathbb {P}*\dot {\mathbb {Q}},\mathcal {U},(\langle r_n:n\in \omega \rangle , h_0)\in \mathcal {M}$
, and let
$p,\dot {f},\mathbb {P}*\dot {\mathbb {Q}},\mathcal {U},(\langle r_n:n\in \omega \rangle , h_0)\in \mathcal {M}$
, and let
![]() $Z\in \mathcal {U}$
be a pseudointersection of
$Z\in \mathcal {U}$
be a pseudointersection of
![]() $\mathcal {U}\cap \mathcal {M}$
. Let
$\mathcal {U}\cap \mathcal {M}$
. Let
![]() $m\in \omega $
be such that
$m\in \omega $
be such that
![]() $\varphi (h_0[Z])<m$
. Then for all
$\varphi (h_0[Z])<m$
. Then for all
![]() $n\in \omega $
, there are the following:
$n\in \omega $
, there are the following:
-
(1) An
 $(\mathcal {M},\mathbb {P})$
-generic condition
$(\mathcal {M},\mathbb {P})$
-generic condition
 $p_{n,\mathcal {M}}$
.
$p_{n,\mathcal {M}}$
. -
(2) A
 $\mathbb {P}$
-name
$\mathbb {P}$
-name
 $\tilde {s}_n$
.
$\tilde {s}_n$
. -
(3) A
 $\mathbb {P}$
-name
$\mathbb {P}$
-name
 $\tilde {h}_n$
for a finite to one function from
$\tilde {h}_n$
for a finite to one function from
 $\omega $
to
$\omega $
to
 $\omega $
.
$\omega $
. -
(4) A
 $\mathbb {P}$
-name
$\mathbb {P}$
-name
 for a sequence of conditions in
for a sequence of conditions in
 $\dot {\mathbb {Q}}[\dot {G}_{\mathbb {P}}]$
.
$\dot {\mathbb {Q}}[\dot {G}_{\mathbb {P}}]$
.
Such that:
-
(i)
 $p_{n,\mathcal {M}}\leq p_0$
.
$p_{n,\mathcal {M}}\leq p_0$
. -
(ii)
 $p_{n,\mathcal {M}}\Vdash ` `\tilde {s}_n\leq \dot {q}"$
and
$p_{n,\mathcal {M}}\Vdash ` `\tilde {s}_n\leq \dot {q}"$
and
 $p_{n,\mathcal {M}}\Vdash ` `\tilde {s}_n\in \dot {\mathbb {Q}}[\dot {G}_{\mathbb {P}}]\cap \mathcal {M}[\dot {G}_{\mathbb {P}}]"$
.
$p_{n,\mathcal {M}}\Vdash ` `\tilde {s}_n\in \dot {\mathbb {Q}}[\dot {G}_{\mathbb {P}}]\cap \mathcal {M}[\dot {G}_{\mathbb {P}}]"$
. -
(iii)
 $p_{n,\mathcal {M}}$
forces that
$p_{n,\mathcal {M}}$
forces that
 is a fine interpretation of
is a fine interpretation of
 $\dot {f}$
below
$\dot {f}$
below
 $\tilde {s}_n$
and such that
$\tilde {s}_n$
and such that
 $\varphi (\tilde {h}_n[Z])<m$
.
$\varphi (\tilde {h}_n[Z])<m$
. -
(iv)
 $p_{n,\mathcal {M}}\Vdash ` `\tilde {s}_n\Vdash ` `\dot {f}\upharpoonright n=\tilde {h}_n\upharpoonright n""$
.
$p_{n,\mathcal {M}}\Vdash ` `\tilde {s}_n\Vdash ` `\dot {f}\upharpoonright n=\tilde {h}_n\upharpoonright n""$
.
Proof Fix a natural number
![]() $n\in \omega $
. We need to find the objects in clauses 1)–4). First note that by Lemma 5.4, we can find inside
$n\in \omega $
. We need to find the objects in clauses 1)–4). First note that by Lemma 5.4, we can find inside
![]() $\mathcal {M}$
a
$\mathcal {M}$
a
![]() $\mathbb {P}$
-name for a fine derived sequence
$\mathbb {P}$
-name for a fine derived sequence
![]() $\dot {\delta }=\dot {\delta }(\langle r_n:n\in \omega \rangle ,\dot {f})$
such that
$\dot {\delta }=\dot {\delta }(\langle r_n:n\in \omega \rangle ,\dot {f})$
such that
![]() $\textrm{int}(\dot {\delta },\dot {f})$
is interpreted by
$\textrm{int}(\dot {\delta },\dot {f})$
is interpreted by
![]() $\langle p_n:n\in \omega \rangle $
as
$\langle p_n:n\in \omega \rangle $
as
![]() $h_0$
. For short, denote by
$h_0$
. For short, denote by
![]() $\dot {h}$
the name
$\dot {h}$
the name
![]() $\textrm{int}(\dot {\delta },\dot {f})$
.
$\textrm{int}(\dot {\delta },\dot {f})$
.
Let
![]() $G\subseteq \mathbb {P}$
be a generic filter over V. By hypothesis,
$G\subseteq \mathbb {P}$
be a generic filter over V. By hypothesis,
![]() $\mathcal {U}$
remains as an
$\mathcal {U}$
remains as an
![]() $(\mathscr {I},p)$
-point in
$(\mathscr {I},p)$
-point in
![]() $V[G]$
, and by elementarity,
$V[G]$
, and by elementarity,
![]() $\mathcal {M}[G]\vDash \mathcal {U}\text { is an } (\mathscr {I},p)\text {-point}$
. So for each
$\mathcal {M}[G]\vDash \mathcal {U}\text { is an } (\mathscr {I},p)\text {-point}$
. So for each
![]() $k\in \omega $
, there are
$k\in \omega $
, there are
![]() $u_k\leq p_k$
and
$u_k\leq p_k$
and
![]() $X_k\in \mathcal {U}$
such that
$X_k\in \mathcal {U}$
such that
![]() $u_k\Vdash ` `\varphi (\dot {h}[X_k])<1"$
, since
$u_k\Vdash ` `\varphi (\dot {h}[X_k])<1"$
, since
![]() $\mathscr {I}=Exh(\varphi )$
. Clearly this can by done inside
$\mathscr {I}=Exh(\varphi )$
. Clearly this can by done inside
![]() $\mathcal {M}$
, so we assume these two sequences are in
$\mathcal {M}$
, so we assume these two sequences are in
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $X\in \mathcal {M}\cap \mathcal {U}$
be a pseudointersection of
$X\in \mathcal {M}\cap \mathcal {U}$
be a pseudointersection of
![]() $\langle X_k:k\in \omega \rangle $
. Now, working in
$\langle X_k:k\in \omega \rangle $
. Now, working in
![]() $\mathcal {M}$
, define by recursion a sequence of natural numbers
$\mathcal {M}$
, define by recursion a sequence of natural numbers
![]() $\langle k_l:l\in \omega \rangle $
as follows:
$\langle k_l:l\in \omega \rangle $
as follows:
-
(1)
 $k_0=0.$
$k_0=0.$
-
(2) For all
 $i\leq k_l$
,
$i\leq k_l$
,
 $X\setminus k_{l+1}\subseteq X_i$
.
$X\setminus k_{l+1}\subseteq X_i$
. -
(3) For all
 $i\ge k_{l+1}$
,
$i\ge k_{l+1}$
,
 $p_i\Vdash ` `\dot {h}\upharpoonright k_l= h_0\upharpoonright k_l".$
$p_i\Vdash ` `\dot {h}\upharpoonright k_l= h_0\upharpoonright k_l".$
-
(4) For all
 $i\leq k_l$
, there is
$i\leq k_l$
, there is
 $u_i^{l+1}\leq u_i\leq p_i$
such that
$u_i^{l+1}\leq u_i\leq p_i$
such that
 $u_i^{l+1}\Vdash ` `\varphi (\dot {h}[X_i\setminus k_{l+1}])<m-\max \{\varphi (h_0[F]):F\subseteq k_l\land \varphi (h_0[F])<m\}"$
.
$u_i^{l+1}\Vdash ` `\varphi (\dot {h}[X_i\setminus k_{l+1}])<m-\max \{\varphi (h_0[F]):F\subseteq k_l\land \varphi (h_0[F])<m\}"$
.
Note that 4) can be achieved since
![]() $\dot {h}$
is forced to be finite to one, and
$\dot {h}$
is forced to be finite to one, and
![]() $u_i$
forces
$u_i$
forces
![]() $\dot {h}[X_i]\in \mathscr {I}=Exh(\varphi )$
. Conditions 1)–3) are easy to arrange.
$\dot {h}[X_i]\in \mathscr {I}=Exh(\varphi )$
. Conditions 1)–3) are easy to arrange.
Assume the sequence
![]() $\langle k_j:j\in \omega \rangle $
has been constructed. Without loss of generality, we can assume that
$\langle k_j:j\in \omega \rangle $
has been constructed. Without loss of generality, we can assume that
![]() $Y=\bigcup _{j\in \omega }[k_{3j+1},k_{3j+2})\in \mathcal U$
. Let
$Y=\bigcup _{j\in \omega }[k_{3j+1},k_{3j+2})\in \mathcal U$
. Let
![]() $j_0$
be such that
$j_0$
be such that
![]() $Z\setminus k_{3j_0}\subseteq X\cap Y$
(recall that Z is a pseudointersection of
$Z\setminus k_{3j_0}\subseteq X\cap Y$
(recall that Z is a pseudointersection of
![]() $\mathcal M\cap \mathcal U$
, and
$\mathcal M\cap \mathcal U$
, and
![]() $X\cap Y\in \mathcal U\cap \mathcal M$
). Note that for any
$X\cap Y\in \mathcal U\cap \mathcal M$
). Note that for any
![]() $l> j_0$
we have
$l> j_0$
we have
![]() $[k_{3l-1},k_{3l+1})\cap Z=\emptyset $
. Fix one of such l. We claim that
$[k_{3l-1},k_{3l+1})\cap Z=\emptyset $
. Fix one of such l. We claim that
![]() $u_{k_{3l}}^{3l+1}\Vdash ` `\varphi (\dot {h}[Z])< m"$
. Since
$u_{k_{3l}}^{3l+1}\Vdash ` `\varphi (\dot {h}[Z])< m"$
. Since
![]() $u_{k_{3l}}^{3l+1}\leq p_{k_{3l}}$
, by 3) above we have
$u_{k_{3l}}^{3l+1}\leq p_{k_{3l}}$
, by 3) above we have
which in turn implies
and so
Also, by 2) and the choice of l we have
Note that since
![]() $Z\cap [k_{3l-1},k_{3l+1})=\emptyset $
, the following holds:
$Z\cap [k_{3l-1},k_{3l+1})=\emptyset $
, the following holds:
 $$ \begin{align} u_{k_{3l}}^{3l+1}\Vdash ` `\varphi(\dot{h}[Z])\leq\varphi(\dot{h}[Z\setminus k_{3l}])+\varphi &(\dot{h}[Z\cap k_{3l}])= \\ &\qquad \varphi(\dot{h}[Z\setminus k_{3l+1}])+\varphi(\dot{h}[Z\cap k_{3l-1}])". \nonumber \end{align} $$
$$ \begin{align} u_{k_{3l}}^{3l+1}\Vdash ` `\varphi(\dot{h}[Z])\leq\varphi(\dot{h}[Z\setminus k_{3l}])+\varphi &(\dot{h}[Z\cap k_{3l}])= \\ &\qquad \varphi(\dot{h}[Z\setminus k_{3l+1}])+\varphi(\dot{h}[Z\cap k_{3l-1}])". \nonumber \end{align} $$
Note that (1) implies the following:
This inequality, joint with 4), gives the following:
or equivalently
By (2) and the monotonicity of
![]() $\varphi $
, we have that
$\varphi $
, we have that
Finally by (3) we get
Now let
![]() $l>j_0$
be a natural number big enough so that
$l>j_0$
be a natural number big enough so that
![]() $n<k_{3l-1}$
, and let
$n<k_{3l-1}$
, and let
![]() $q\leq u_{k_{3l}}^{3l+1}$
be an
$q\leq u_{k_{3l}}^{3l+1}$
be an
![]() $(\mathcal {M},{\mathbb {P}})$
-generic condition. Define the following:
$(\mathcal {M},{\mathbb {P}})$
-generic condition. Define the following:
-
(a) In
 $\mathcal {M}$
, let
$\mathcal {M}$
, let
 $\tilde {s}_n$
be the
$\tilde {s}_n$
be the
 $\mathbb {P}$
-name
$\mathbb {P}$
-name
 $\dot {q}_{k_{3l}}$
.
$\dot {q}_{k_{3l}}$
. -
(b) In
 $\mathcal {M}$
, let
$\mathcal {M}$
, let
 be a
be a
 $\mathbb {P}$
-name for the fine derived sequence
$\mathbb {P}$
-name for the fine derived sequence
 $\tilde {\delta }(\langle r^{\prime }_i:i\in \omega \rangle ,\dot {f})$
, where
$\tilde {\delta }(\langle r^{\prime }_i:i\in \omega \rangle ,\dot {f})$
, where
 $r^{\prime }_i=r_{i+k_{3l}}$
, for all
$r^{\prime }_i=r_{i+k_{3l}}$
, for all
 $i\in \omega $
.
$i\in \omega $
. -
(c) In
 $\mathcal {M}$
, let
$\mathcal {M}$
, let
 $\tilde {h}_{n}$
be the
$\tilde {h}_{n}$
be the
 $\mathbb {P}$
-name
$\mathbb {P}$
-name
 $\dot {h}$
.
$\dot {h}$
. -
(d) Define
 $p_{n,\mathcal {M}}=q$
.
$p_{n,\mathcal {M}}=q$
.
We claim that
![]() $p_{n,\mathcal {M}}$
,
$p_{n,\mathcal {M}}$
,
![]() $\tilde {s}_n$
,
$\tilde {s}_n$
,
![]() $\tilde {h}_n$
and
$\tilde {h}_n$
and
![]() are as required.
are as required.
Conditions (1)–(4) are easily seen to be hold by the construction. Condition
![]() $i)$
, follows from the fact that
$i)$
, follows from the fact that
![]() $p_{n,\mathcal {M}}\leq p_{k_{3l}}\leq p_0$
. The first part of
$p_{n,\mathcal {M}}\leq p_{k_{3l}}\leq p_0$
. The first part of
![]() $ii)$
follows from a) and
$ii)$
follows from a) and
![]() $(p_{k_{3l}},\dot {q}_{k_{3l}})\leq (p,\dot {q})$
and the choice of
$(p_{k_{3l}},\dot {q}_{k_{3l}})\leq (p,\dot {q})$
and the choice of
![]() $\tilde {s}_n$
. The second part of condition
$\tilde {s}_n$
. The second part of condition
![]() $ii)$
follows from the fact that
$ii)$
follows from the fact that
![]() $\langle (p_k,\dot {q}_k):k\in \omega \rangle \in \mathcal {M}$
,
$\langle (p_k,\dot {q}_k):k\in \omega \rangle \in \mathcal {M}$
,
![]() $p_{n,\mathcal {M}}\leq p_{k_{3l}}$
and
$p_{n,\mathcal {M}}\leq p_{k_{3l}}$
and
![]() $\tilde {s}_n=\dot {q}_{k_{3l}}$
.
$\tilde {s}_n=\dot {q}_{k_{3l}}$
.
Let us see condition
![]() $(iii)$
. By definition
$(iii)$
. By definition
![]() $\tilde {\delta }(\langle r_i':i\in \omega \rangle ,\dot {f})$
, is a fine interpretation of
$\tilde {\delta }(\langle r_i':i\in \omega \rangle ,\dot {f})$
, is a fine interpretation of
![]() $\dot {f}$
. To see that
$\dot {f}$
. To see that
![]() $\tilde {\delta }(\langle r_i':i\in \omega \rangle ,\dot {f})$
is forced to be below
$\tilde {\delta }(\langle r_i':i\in \omega \rangle ,\dot {f})$
is forced to be below
![]() $\tilde {s}_n$
by
$\tilde {s}_n$
by
![]() $p_{n,\mathcal {M}}$
, let
$p_{n,\mathcal {M}}$
, let
![]() $G\subseteq \mathbb {P}$
be any generic filter such that
$G\subseteq \mathbb {P}$
be any generic filter such that
![]() $p_{n,\mathcal {M}}\in G$
. By definition
$p_{n,\mathcal {M}}\in G$
. By definition
![]() $r_0'=(p_{k_{3l}},\dot {q}_{k_{3l}})$
. Since
$r_0'=(p_{k_{3l}},\dot {q}_{k_{3l}})$
. Since
![]() $p_{n,\mathcal {M}}\leq p_{k_{3l}}$
and
$p_{n,\mathcal {M}}\leq p_{k_{3l}}$
and
![]() $p_{n,\mathcal {M}}\in G$
, it follows that the first term of
$p_{n,\mathcal {M}}\in G$
, it follows that the first term of
![]() $\tilde {\delta }(\langle r_i':i\in \omega \rangle )$
is
$\tilde {\delta }(\langle r_i':i\in \omega \rangle )$
is
![]() $\dot {q}_{k_{3l}}[G]=\tilde {s}_n[G]$
, and all the remaining terms are below the first one since
$\dot {q}_{k_{3l}}[G]=\tilde {s}_n[G]$
, and all the remaining terms are below the first one since
![]() $\tilde {\delta }(\langle r_i':i\in \omega \rangle ,\dot {f})$
is a decreasing sequence. To see that
$\tilde {\delta }(\langle r_i':i\in \omega \rangle ,\dot {f})$
is a decreasing sequence. To see that
![]() $p_{n,\mathcal {M}}\Vdash ` `\varphi (\tilde {h}_n[Z])<m"$
, recall that
$p_{n,\mathcal {M}}\Vdash ` `\varphi (\tilde {h}_n[Z])<m"$
, recall that
![]() $l>j_0$
,
$l>j_0$
,
![]() $p_{n,\mathcal {M}}\leq u_{k_{3l}}^{3l+1}$
and
$p_{n,\mathcal {M}}\leq u_{k_{3l}}^{3l+1}$
and
![]() $u_{k_{kl}}^{3l+1}\Vdash ` `\varphi (\dot {h}[Z])<m"$
.
$u_{k_{kl}}^{3l+1}\Vdash ` `\varphi (\dot {h}[Z])<m"$
.
To see that condition
![]() $(iv)$
holds, just note that
$(iv)$
holds, just note that
![]() $n < k_{3l-1}$
,
$n < k_{3l-1}$
,
![]() $(p_{n,\mathcal {M}},\tilde {s}_n)\leq (p_{k_{3l}},\dot {q}_{k_{3l}})$
and
$(p_{n,\mathcal {M}},\tilde {s}_n)\leq (p_{k_{3l}},\dot {q}_{k_{3l}})$
and
which implies
and also
so it follows that
Since
![]() $n<k_{3l-1}$
, the required property follows.
$n<k_{3l-1}$
, the required property follows.
Before proving Theorem 5.1 we introduce some notation and conventions to be used in the proof. Given a countable support iteration
![]() $\mathbb {P}=\langle \mathbb {P}_n,\dot {\mathbb {Q}}_n:n\in \omega \rangle $
which is factorized as
$\mathbb {P}=\langle \mathbb {P}_n,\dot {\mathbb {Q}}_n:n\in \omega \rangle $
which is factorized as
![]() $\mathbb {P}=\mathbb {P}_n*\tilde {\mathbb {P}}_{[n+1,\omega )}$
, and a condition
$\mathbb {P}=\mathbb {P}_n*\tilde {\mathbb {P}}_{[n+1,\omega )}$
, and a condition
![]() $p\in \mathbb {P}$
, we denote by
$p\in \mathbb {P}$
, we denote by
![]() $(p_0,\dot {p}_{[1,\omega )})$
the factorization of the condition p relative to
$(p_0,\dot {p}_{[1,\omega )})$
the factorization of the condition p relative to
![]() $\mathbb {P}_n*\tilde {\mathbb {P}}_{[n+1,\omega )}$
. In a similar way, if
$\mathbb {P}_n*\tilde {\mathbb {P}}_{[n+1,\omega )}$
. In a similar way, if
![]() $\langle r_n:n\in \omega \rangle $
is a sequence of conditions in
$\langle r_n:n\in \omega \rangle $
is a sequence of conditions in
![]() $\mathbb {P}$
, we denote by
$\mathbb {P}$
, we denote by
![]() $(r_0^k,\dot {r}_{[1,\omega )}^k)$
the factorization of the condition
$(r_0^k,\dot {r}_{[1,\omega )}^k)$
the factorization of the condition
![]() $r_k$
relative to
$r_k$
relative to
![]() $\mathbb {P}_n*\tilde {\mathbb {P}}_{[n+1,\omega )}$
. On the other hand, consider
$\mathbb {P}_n*\tilde {\mathbb {P}}_{[n+1,\omega )}$
. On the other hand, consider
![]() $\mathbb {P}$
factorized as
$\mathbb {P}$
factorized as
![]() $\mathbb {P}_n*\dot {\mathbb {Q}}_{n+1}*\tilde {\mathbb {P}}_{[n+2,\omega )}$
and let
$\mathbb {P}_n*\dot {\mathbb {Q}}_{n+1}*\tilde {\mathbb {P}}_{[n+2,\omega )}$
and let
![]() $G_{n}\subseteq \mathbb {P}_{n}$
be a generic filter over V. We will be translating
$G_{n}\subseteq \mathbb {P}_{n}$
be a generic filter over V. We will be translating
![]() $\dot {\mathbb {Q}}_{n+1}[G_{n}]$
-names in
$\dot {\mathbb {Q}}_{n+1}[G_{n}]$
-names in
![]() $V[G_n]$
to
$V[G_n]$
to
![]() $\mathbb {P}_{n+1}$
-names names in V, and vice versa. In this setting, when working in
$\mathbb {P}_{n+1}$
-names names in V, and vice versa. In this setting, when working in
![]() $V[G_n]$
, we consider
$V[G_n]$
, we consider
![]() $\dot {\mathbb {Q}}_{n+1}[G_n]$
as the evaluation of the
$\dot {\mathbb {Q}}_{n+1}[G_n]$
as the evaluation of the
![]() $\mathbb {P}_n$
-name
$\mathbb {P}_n$
-name
![]() $\dot {\mathbb {Q}}_{n+1}$
, and
$\dot {\mathbb {Q}}_{n+1}$
, and
![]() $\tilde {\mathbb {P}}_{[n+2,\omega )}[G_n]$
as a suitable
$\tilde {\mathbb {P}}_{[n+2,\omega )}[G_n]$
as a suitable
![]() $\dot {\mathbb {Q}}_{n+1}[G_n]$
-name for the residual iteration after
$\dot {\mathbb {Q}}_{n+1}[G_n]$
-name for the residual iteration after
![]() $\mathbb {P}_{n+1}=\mathbb {P}_n*\dot {\mathbb {Q}}_{n+1}$
, or more exactly, for the quotient
$\mathbb {P}_{n+1}=\mathbb {P}_n*\dot {\mathbb {Q}}_{n+1}$
, or more exactly, for the quotient
![]() $\mathbb {P}_{\omega }/G_{n+1}$
, where
$\mathbb {P}_{\omega }/G_{n+1}$
, where
![]() $G_{n+1}\subseteq \mathbb {P}_{n+1}$
is a generic filter over V. So, when working in
$G_{n+1}\subseteq \mathbb {P}_{n+1}$
is a generic filter over V. So, when working in
![]() $V[G_n]$
, we will write
$V[G_n]$
, we will write
![]() $\dot {\mathbb {Q}}_{n+1}[G_n]*\tilde {\mathbb {P}}_{n+1}[G_n]$
for the quotient forcing
$\dot {\mathbb {Q}}_{n+1}[G_n]*\tilde {\mathbb {P}}_{n+1}[G_n]$
for the quotient forcing
![]() $\mathbb {P}_{\omega }/G_n$
in
$\mathbb {P}_{\omega }/G_n$
in
![]() $V[G_n]$
. The point of this is the two step factorization of
$V[G_n]$
. The point of this is the two step factorization of
![]() $\mathbb {P}_{\omega }/G_n$
, so we can apply the previous lemma in
$\mathbb {P}_{\omega }/G_n$
, so we can apply the previous lemma in
![]() $V[G_n]$
, and then make a translation of elements from
$V[G_n]$
, and then make a translation of elements from
![]() $V[G_n]$
to
$V[G_n]$
to
![]() $\mathbb {P}_n$
-names in V. Finally, we will be making an abuse of notation when referring to the
$\mathbb {P}_n$
-names in V. Finally, we will be making an abuse of notation when referring to the
![]() $\mathbb {P}_{\omega }$
-name
$\mathbb {P}_{\omega }$
-name
![]() $\dot {f}$
: when talking about
$\dot {f}$
: when talking about
![]() $\dot {f}$
in the extensions given by
$\dot {f}$
in the extensions given by
![]() $\mathbb {P}_n$
, we implicitly assume that we are taking about an appropriated
$\mathbb {P}_n$
, we implicitly assume that we are taking about an appropriated
![]() $\mathbb {P}_{[n+1,\omega )}$
-name which is equivalent to
$\mathbb {P}_{[n+1,\omega )}$
-name which is equivalent to
![]() $\dot {f}$
after forcing with
$\dot {f}$
after forcing with
![]() $\mathbb {P}_{[n+1,\omega )}$
on the generic extension by
$\mathbb {P}_{[n+1,\omega )}$
on the generic extension by
![]() $\mathbb {P}_n$
.
$\mathbb {P}_n$
.
Proof of Theorem 5.1
Let us first note that the successor step is easy to handle: let
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
be a two step iteration of proper forcings such that
$\mathbb {P}*\dot {\mathbb {Q}}$
be a two step iteration of proper forcings such that
![]() $\mathbb {P}$
preserves
$\mathbb {P}$
preserves
![]() $(\mathscr {I},p)$
-points and
$(\mathscr {I},p)$
-points and
![]() $\mathbb {P}\Vdash ` `\dot {\mathbb {Q}}\text { preserves } (\mathscr {I},p)\text {-points}"$
. Let
$\mathbb {P}\Vdash ` `\dot {\mathbb {Q}}\text { preserves } (\mathscr {I},p)\text {-points}"$
. Let
![]() $\mathcal {U}$
be an
$\mathcal {U}$
be an
![]() $(\mathscr {I},p)$
-point in the ground model. Let
$(\mathscr {I},p)$
-point in the ground model. Let
![]() $G\subseteq \mathbb {P}$
be V-generic. Then, in
$G\subseteq \mathbb {P}$
be V-generic. Then, in
![]() $V[G]$
,
$V[G]$
,
![]() $\mathcal {U}$
generates a
$\mathcal {U}$
generates a
![]() $(\mathscr {I},p)$
-point, and
$(\mathscr {I},p)$
-point, and
![]() $\dot {\mathbb {Q}}[G]$
preserves
$\dot {\mathbb {Q}}[G]$
preserves
![]() $(\mathscr {I},p)$
-points. If
$(\mathscr {I},p)$
-points. If
![]() $H\subseteq \dot {\mathbb {Q}}$
is
$H\subseteq \dot {\mathbb {Q}}$
is
![]() $V[G]$
-generic, then
$V[G]$
-generic, then
![]() $\mathcal {U}$
generates an
$\mathcal {U}$
generates an
![]() $(\mathscr {I},p)$
-point in
$(\mathscr {I},p)$
-point in
![]() $V[G][H]=V[G*H]$
. So
$V[G][H]=V[G*H]$
. So
![]() $\mathbb {P}*\dot {\mathbb {Q}}$
preserves
$\mathbb {P}*\dot {\mathbb {Q}}$
preserves
![]() $\mathcal {U}$
as an
$\mathcal {U}$
as an
![]() $(\mathscr {I},p)$
-point.
$(\mathscr {I},p)$
-point.
We are left with the limit step. Let us assume all the hypothesis in the statement of Theorem 5.1. Note that we can assume that the iteration has length
![]() $\omega $
, since every real appears in a successor stage or in a countable cofinality stage, so we assume
$\omega $
, since every real appears in a successor stage or in a countable cofinality stage, so we assume
![]() $\mathbb {P}_{\omega }=\langle \mathbb {P}_n,\dot {\mathbb {Q}}_n:n\in \omega \rangle $
. Let
$\mathbb {P}_{\omega }=\langle \mathbb {P}_n,\dot {\mathbb {Q}}_n:n\in \omega \rangle $
. Let
![]() $\mathcal U$
be an
$\mathcal U$
be an
![]() $(\mathscr {I},p)$
-point,
$(\mathscr {I},p)$
-point,
![]() $\dot f$
a
$\dot f$
a
![]() $\mathbb P_{\omega }$
-name for a function from
$\mathbb P_{\omega }$
-name for a function from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
and
$\omega $
and
![]() $p\in \mathbb P_{\omega }$
a condition. Note that by Theorem 2.8, we have that
$p\in \mathbb P_{\omega }$
a condition. Note that by Theorem 2.8, we have that
![]() $\mathcal {U}$
generates a p-point after forcing with
$\mathcal {U}$
generates a p-point after forcing with
![]() $\mathbb {P}_{\omega }$
, so we can assume that
$\mathbb {P}_{\omega }$
, so we can assume that
![]() $p\Vdash ` `\mathcal {U}\text { generates a } p\text {-point}"$
. If there is a condition
$p\Vdash ` `\mathcal {U}\text { generates a } p\text {-point}"$
. If there is a condition
![]() $q\leq p$
and
$q\leq p$
and
![]() $X\in \mathcal U$
such that
$X\in \mathcal U$
such that
![]() $q\Vdash ` `\dot {f}\upharpoonright X \textit {is constant}"$
, then we are done. Otherwise, there is
$q\Vdash ` `\dot {f}\upharpoonright X \textit {is constant}"$
, then we are done. Otherwise, there is
![]() $q\leq p$
and there exists
$q\leq p$
and there exists
![]() $A\in \mathcal U$
such that
$A\in \mathcal U$
such that
![]() $\dot f\upharpoonright A$
is forced to be finite to one by q, so we can assume that
$\dot f\upharpoonright A$
is forced to be finite to one by q, so we can assume that
![]() $\dot f$
is finite to one. Let
$\dot f$
is finite to one. Let
![]() $\mathcal M\prec H(\theta )$
be a countable elementary submodel such that
$\mathcal M\prec H(\theta )$
be a countable elementary submodel such that
![]() $\dot {f},\mathcal U,p,\mathbb P_{\omega }\in \mathcal M$
. Fix
$\dot {f},\mathcal U,p,\mathbb P_{\omega }\in \mathcal M$
. Fix
![]() $Z\in \mathcal U$
a pseudointersection of
$Z\in \mathcal U$
a pseudointersection of
![]() $\mathcal U\cap \mathcal M$
. In
$\mathcal U\cap \mathcal M$
. In
![]() $\mathcal M$
, let
$\mathcal M$
, let
![]() $(\langle r_n:n\in \omega \rangle ,h_0)$
be a fine interpretation for
$(\langle r_n:n\in \omega \rangle ,h_0)$
be a fine interpretation for
![]() $\dot {f}$
below p, and assume
$\dot {f}$
below p, and assume
![]() $\varphi (h_0[Z])< m$
for some fixed
$\varphi (h_0[Z])< m$
for some fixed
![]() $m\in \omega $
. For each
$m\in \omega $
. For each
![]() $n\in \omega $
, we assume
$n\in \omega $
, we assume
![]() $r_n$
has the form
$r_n$
has the form
![]() $\langle r_n^k:k\in \omega \rangle $
. We will construct by recursion four sequences
$\langle r_n^k:k\in \omega \rangle $
. We will construct by recursion four sequences
![]() $\langle q_n:n\in \omega \rangle $
,
$\langle q_n:n\in \omega \rangle $
,
![]() $\langle \dot {s}_n:n\in \omega \rangle $
,
$\langle \dot {s}_n:n\in \omega \rangle $
,
![]() $\langle \dot {h}_n:n\in \omega \rangle $
and
$\langle \dot {h}_n:n\in \omega \rangle $
and
![]() such that the following holds:
such that the following holds:
-
(a) For
 $n=0$
,
$n=0$
,
 $q_0$
is a
$q_0$
is a
 $(\mathcal {M},\mathbb {P}_0)$
-generic condition.
$(\mathcal {M},\mathbb {P}_0)$
-generic condition. -
(b) For all
 $n\in \omega $
,
$n\in \omega $
,
 $q_n$
is
$q_n$
is
 $(\mathcal {M},\mathbb {P}_n)$
-generic and
$(\mathcal {M},\mathbb {P}_n)$
-generic and
 $q_{n}=(q_0,\ldots ,\dot {q}_n)$
, where
$q_{n}=(q_0,\ldots ,\dot {q}_n)$
, where
 $\dot {q}_n$
is a
$\dot {q}_n$
is a
 $\mathbb {P}_{n-1}$
-name for
$\mathbb {P}_{n-1}$
-name for
 $n>0$
.
$n>0$
. -
(c) For all positive
 $n\in \omega $
,
$n\in \omega $
,
 $\dot {h}_n$
is a
$\dot {h}_n$
is a
 $\mathbb {P}_{n-1}$
-name and
$\mathbb {P}_{n-1}$
-name and
 $q_{n-1}\Vdash ` `\dot {h}_n\in \mathcal {M}[\dot {G}_{\mathbb {P}_{n-1}}]"$
.
$q_{n-1}\Vdash ` `\dot {h}_n\in \mathcal {M}[\dot {G}_{\mathbb {P}_{n-1}}]"$
. -
(d) For all positive
 $n\in \omega $
,
$n\in \omega $
,
 is a
is a
 $\mathbb {P}_{n-1}$
-name for a decreasing sequence of conditions in
$\mathbb {P}_{n-1}$
-name for a decreasing sequence of conditions in
 $\tilde {\mathbb {P}}_{[n,\omega )}[\dot {G}_{\mathbb {P}_{n-1}}]$
.
$\tilde {\mathbb {P}}_{[n,\omega )}[\dot {G}_{\mathbb {P}_{n-1}}]$
. -
(e) For all positive
 $n\in \omega $
,
$n\in \omega $
,
 $\dot {s}_n$
is a
$\dot {s}_n$
is a
 $\mathbb {P}_{n-1}$
-name and
$\mathbb {P}_{n-1}$
-name and
 $q_{n-1}$
forces that
$q_{n-1}$
forces that
 $\dot {s}_n$
is a condition in
$\dot {s}_n$
is a condition in
 $\tilde {\mathbb {P}}_{[n,\omega )}[\dot {G}_{\mathbb {P}_{n-1}}]\cap \mathcal {M}[\dot {G}_{\mathbb {P}_{n-1}}]$
.
$\tilde {\mathbb {P}}_{[n,\omega )}[\dot {G}_{\mathbb {P}_{n-1}}]\cap \mathcal {M}[\dot {G}_{\mathbb {P}_{n-1}}]$
. -
(f) For all positive
 $n\in \omega $
,
$n\in \omega $
,
 $q_{n-1}$
forces that
$q_{n-1}$
forces that
 is a fine interpretation of
is a fine interpretation of
 $\dot {f}$
below
$\dot {f}$
below
 $\dot {s}_n$
.
$\dot {s}_n$
. -
(g) For all positive
 $n\in \omega $
,
$n\in \omega $
,
 $q_{n-1}$
forces that
$q_{n-1}$
forces that
 $\varphi (\dot {h}_n[Z])<m$
.
$\varphi (\dot {h}_n[Z])<m$
. -
(h) For all positive
 $n\in \omega $
,
$n\in \omega $
,
 $q_{n-1}\Vdash ` `\dot {s}_n\Vdash ` `\dot {f}\upharpoonright n=\dot {h}_n\upharpoonright n""$
.
$q_{n-1}\Vdash ` `\dot {s}_n\Vdash ` `\dot {f}\upharpoonright n=\dot {h}_n\upharpoonright n""$
. -
(i) For all positive
 $n\in \omega $
,
$n\in \omega $
,
 $q_{n-1}\Vdash ` `\dot {q}_n\leq \dot {s}_{0}^n"$
and
$q_{n-1}\Vdash ` `\dot {q}_n\leq \dot {s}_{0}^n"$
and
 $q_0\leq r_0^0$
.
$q_0\leq r_0^0$
. -
(j) For all
 $n\in \omega $
,
$n\in \omega $
,
 $q_n\Vdash ` `\dot {s}_{n+1}\leq \dot {s}_{[1,\omega )}^{n}"$
.
$q_n\Vdash ` `\dot {s}_{n+1}\leq \dot {s}_{[1,\omega )}^{n}"$
.
Suppose first we have succeeded in the above construction and consider the condition
![]() $q=\bigcup _{n\in \omega }q_n$
. Note that by construction of q we have
$q=\bigcup _{n\in \omega }q_n$
. Note that by construction of q we have
![]() $q\leq q_0$
. We claim that
$q\leq q_0$
. We claim that
![]() $q\Vdash ` `\varphi (\dot {f}[Z])\leq m"$
. It is enough to prove
$q\Vdash ` `\varphi (\dot {f}[Z])\leq m"$
. It is enough to prove
![]() $q\Vdash "(\forall n\in \omega )(\dot {f}\upharpoonright n=\dot {h}_n\upharpoonright n)"$
, since by g), this would imply that q forces the measure of the initial segments of
$q\Vdash "(\forall n\in \omega )(\dot {f}\upharpoonright n=\dot {h}_n\upharpoonright n)"$
, since by g), this would imply that q forces the measure of the initial segments of
![]() $\dot {f}[Z]$
to be smaller than m, and by the lower semicontinuity of
$\dot {f}[Z]$
to be smaller than m, and by the lower semicontinuity of
![]() $\varphi $
, this implies that
$\varphi $
, this implies that
![]() $\varphi (\dot {f}[Z])$
is at most m. First note that for any positive
$\varphi (\dot {f}[Z])$
is at most m. First note that for any positive
![]() $n\in \omega $
, it holds that
$n\in \omega $
, it holds that
![]() $q_{n}^{\frown } \dot {s}_{n+1}\leq q_{n-1}^{\frown } \dot {s}_{n}$
. To see this fix a positive
$q_{n}^{\frown } \dot {s}_{n+1}\leq q_{n-1}^{\frown } \dot {s}_{n}$
. To see this fix a positive
![]() $n\in \omega $
. Clause j) is equivalent to write
$n\in \omega $
. Clause j) is equivalent to write
![]() $q_{n-1}^{\frown } \dot {q}_n\Vdash ` `\dot {s}_{n+1}\leq \dot {s}_{[1,\omega )}^n"$
. This, together with
$q_{n-1}^{\frown } \dot {q}_n\Vdash ` `\dot {s}_{n+1}\leq \dot {s}_{[1,\omega )}^n"$
. This, together with
![]() $q_{n-1}\Vdash ` `\dot {q}_n\leq \dot {s}_0^n"$
(see clause i)) and the factorization
$q_{n-1}\Vdash ` `\dot {q}_n\leq \dot {s}_0^n"$
(see clause i)) and the factorization
![]() $\dot {s}_{n}=(\dot {s}_0^n,\dot {s}_{[1,\omega )}^n)$
gives the conclusion that
$\dot {s}_{n}=(\dot {s}_0^n,\dot {s}_{[1,\omega )}^n)$
gives the conclusion that
![]() $q_n^{\frown }\dot {s}_{n+1}\leq q_{n-1}^{\frown } \dot {s}_n$
. Then, note that this implies that for all
$q_n^{\frown }\dot {s}_{n+1}\leq q_{n-1}^{\frown } \dot {s}_n$
. Then, note that this implies that for all
![]() $k\ge n$
, it holds that
$k\ge n$
, it holds that
![]() $q_k^{\frown } \dot {s}_{k+1}\leq q_{n-1}^{\frown } \dot {s}_{n}$
. This implies that for all
$q_k^{\frown } \dot {s}_{k+1}\leq q_{n-1}^{\frown } \dot {s}_{n}$
. This implies that for all
![]() $k\in \omega $
,
$k\in \omega $
,
![]() $q\upharpoonright k=q_k\leq q_{n-1}^{\frown } \dot {s}_{n}\upharpoonright k$
, which means that
$q\upharpoonright k=q_k\leq q_{n-1}^{\frown } \dot {s}_{n}\upharpoonright k$
, which means that
![]() $q\leq q_{n-1}^{\frown } \dot {s}_{n}$
. Since clause h) is equivalent to
$q\leq q_{n-1}^{\frown } \dot {s}_{n}$
. Since clause h) is equivalent to
![]() $q_{n-1}^{\frown } \dot {s}_n\Vdash ` `\dot {f}\upharpoonright n=\dot {h}_n\upharpoonright n"$
, we conclude that
$q_{n-1}^{\frown } \dot {s}_n\Vdash ` `\dot {f}\upharpoonright n=\dot {h}_n\upharpoonright n"$
, we conclude that
![]() $q\Vdash ` `\dot {f}\upharpoonright n=\dot {h}_n\upharpoonright n"$
. Finally, since n was an arbitrary positive natural number, we conclude that
$q\Vdash ` `\dot {f}\upharpoonright n=\dot {h}_n\upharpoonright n"$
. Finally, since n was an arbitrary positive natural number, we conclude that
![]() $q\Vdash "(\forall n\in \omega )(\dot {f}\upharpoonright n=\dot {h}_n\upharpoonright n)"$
.
$q\Vdash "(\forall n\in \omega )(\dot {f}\upharpoonright n=\dot {h}_n\upharpoonright n)"$
.
Let us construct the sequences. We start defining
![]() $\dot {s}_0=p_0$
,
$\dot {s}_0=p_0$
,
![]() $\dot {h}_0=h_0$
and
$\dot {h}_0=h_0$
and
![]() . Consider the factorization
. Consider the factorization
![]() $\mathbb {P}=\mathbb {P}_0*\tilde {\mathbb {P}}_{[1,\omega )}$
. Relative to this factorization, any condition r in
$\mathbb {P}=\mathbb {P}_0*\tilde {\mathbb {P}}_{[1,\omega )}$
. Relative to this factorization, any condition r in
![]() $\mathbb {P}_{\omega }$
is factored as
$\mathbb {P}_{\omega }$
is factored as
![]() $r=(r_0,\dot {r}_{[1,\omega )})$
. For the sequence
$r=(r_0,\dot {r}_{[1,\omega )})$
. For the sequence
![]() $\langle r_n:n\in \omega \rangle $
we will write
$\langle r_n:n\in \omega \rangle $
we will write
![]() $r_n=(r_0^n,\dot {r}_{[1,\omega )}^{n})$
. Then note that all conditions from Lemma 5.5 are satisfied for
$r_n=(r_0^n,\dot {r}_{[1,\omega )}^{n})$
. Then note that all conditions from Lemma 5.5 are satisfied for
![]() $\mathscr {I}$
,
$\mathscr {I}$
,
![]() $\varphi $
,
$\varphi $
,
![]() $\mathbb {P}_0*\tilde {\mathbb {P}}_{[1,\omega )}$
,
$\mathbb {P}_0*\tilde {\mathbb {P}}_{[1,\omega )}$
,
![]() $\mathcal {U}$
,
$\mathcal {U}$
,
![]() $\dot {f}$
,
$\dot {f}$
,
![]() $p=(p_0,\dot {p}_{[1,\omega )})$
,
$p=(p_0,\dot {p}_{[1,\omega )})$
,
![]() $(\langle r_n:n\in \omega \rangle ,h_0),\ Z$
,
$(\langle r_n:n\in \omega \rangle ,h_0),\ Z$
,
![]() $m,$
and
$m,$
and
![]() $\mathcal {M}$
. So for
$\mathcal {M}$
. So for
![]() $n=1$
, by an application of Lemma 5.5 we get
$n=1$
, by an application of Lemma 5.5 we get
![]() $q_{1,\mathcal {M}}$
,
$q_{1,\mathcal {M}}$
,
![]() $\tilde {s}_1$
,
$\tilde {s}_1$
,
![]() $\tilde {h}_1$
,
$\tilde {h}_1$
,
![]() that satisfy conditions 1)
that satisfy conditions 1)
![]() $-$
4) from Lemma 5.5, and such that conditions
$-$
4) from Lemma 5.5, and such that conditions
![]() $i)$
–
$i)$
–
![]() $iv)$
are adapted as follows:
$iv)$
are adapted as follows:
-
(1)
 $q_{1,\mathcal {M}}\leq r_0^0$
is a
$q_{1,\mathcal {M}}\leq r_0^0$
is a
 $(\mathcal {M},\mathbb {P}_0)$
-generic condition.
$(\mathcal {M},\mathbb {P}_0)$
-generic condition. -
(2)
 $q_{1,\mathcal {M}}\Vdash ` `\tilde {s}_{1}\leq \dot {p}_{[1,\omega )}"$
and
$q_{1,\mathcal {M}}\Vdash ` `\tilde {s}_{1}\leq \dot {p}_{[1,\omega )}"$
and
 $q_{\mathcal {M}}\Vdash ` `\tilde {s}_{1}\in \tilde {\mathbb {P}}_{[1,\omega )}[\dot {G}_{\mathbb {P}_0}]\cap \mathcal {M}[\dot {G}_{\mathbb {P}_0}]"$
.
$q_{\mathcal {M}}\Vdash ` `\tilde {s}_{1}\in \tilde {\mathbb {P}}_{[1,\omega )}[\dot {G}_{\mathbb {P}_0}]\cap \mathcal {M}[\dot {G}_{\mathbb {P}_0}]"$
. -
(3)
 $q_{1,\mathcal {M}}$
forces that
$q_{1,\mathcal {M}}$
forces that
 is a fine interpretation of
is a fine interpretation of
 $\dot {f}$
below
$\dot {f}$
below
 $\tilde {s}_1$
, as well as
$\tilde {s}_1$
, as well as
 $\varphi (\tilde {h}_1[Z])<m$
.
$\varphi (\tilde {h}_1[Z])<m$
. -
(4)
 $q_{1,\mathcal {M}}\Vdash ` `\tilde {s}_1\Vdash ` `\dot {f}\upharpoonright 1=\tilde {h}_1\upharpoonright 1""$
.
$q_{1,\mathcal {M}}\Vdash ` `\tilde {s}_1\Vdash ` `\dot {f}\upharpoonright 1=\tilde {h}_1\upharpoonright 1""$
.
Now define
![]() $\dot {q}_0=q_{1,\mathcal {M}}$
,
$\dot {q}_0=q_{1,\mathcal {M}}$
,
![]() $\dot {s}_1=\tilde {s}_1$
,
$\dot {s}_1=\tilde {s}_1$
,
![]() $\dot {h}_1=\tilde {h}_1$
, and
$\dot {h}_1=\tilde {h}_1$
, and
![]() just as was obtained. Let us see that conditions a)–j) are satisfied. Conditions a) and b) follow trivially from 1) above. Condition c) follows from 3) above. Condition d) follows from 3) above. Condition e) follows from 2) above. Conditions f) and g) follow from 3) above. Condition h) is condition 4) above. Condition i) follows from 1) and 2). Condition j) follows from 2).
just as was obtained. Let us see that conditions a)–j) are satisfied. Conditions a) and b) follow trivially from 1) above. Condition c) follows from 3) above. Condition d) follows from 3) above. Condition e) follows from 2) above. Conditions f) and g) follow from 3) above. Condition h) is condition 4) above. Condition i) follows from 1) and 2). Condition j) follows from 2).
Now assume that we have constructed
![]() $q_{n-1}$
,
$q_{n-1}$
,
![]() $\dot {s}_n$
,
$\dot {s}_n$
,
![]() $\dot {h}_n,$
and
$\dot {h}_n,$
and
![]() with the required properties. Consider the factorization
with the required properties. Consider the factorization
![]() $\mathbb {P}_{\omega }=\mathbb {P}_{n-1}*\dot {\mathbb {Q}}_{n}*\tilde {\mathbb {P}}_{[n+1,\omega )}$
. Let
$\mathbb {P}_{\omega }=\mathbb {P}_{n-1}*\dot {\mathbb {Q}}_{n}*\tilde {\mathbb {P}}_{[n+1,\omega )}$
. Let
![]() $G_{n-1}\subseteq \mathbb {P}_{n-1}$
be a generic filter over V such that
$G_{n-1}\subseteq \mathbb {P}_{n-1}$
be a generic filter over V such that
![]() $q_{n-1}\in G_{n-1}$
. Then let
$q_{n-1}\in G_{n-1}$
. Then let
![]() $s_n=\dot {s}_n[G_{n-1}]$
,
$s_n=\dot {s}_n[G_{n-1}]$
,
![]() $h_{n}=\dot {h}_{n}[G_{n-1}],$
and
$h_{n}=\dot {h}_{n}[G_{n-1}],$
and
![]() $\vec {t}_n$
be the evaluations of
$\vec {t}_n$
be the evaluations of
![]() $\dot {s}_{n}$
,
$\dot {s}_{n}$
,
![]() $\dot {h}_n,$
and
$\dot {h}_n,$
and
![]() , respectively, by the filter
, respectively, by the filter
![]() $G_{n-1}$
. We work in
$G_{n-1}$
. We work in
![]() $\mathcal {M}[G_{n-1}]$
. Then we have that
$\mathcal {M}[G_{n-1}]$
. Then we have that
![]() $\dot {\mathbb {Q}}_{n}[G_{n-1}]*\tilde {\mathbb {P}}_{[n+1,\omega )}[G_{n-1}]\in \mathcal {M}[G_{n-1}]$
. Moreover,
$\dot {\mathbb {Q}}_{n}[G_{n-1}]*\tilde {\mathbb {P}}_{[n+1,\omega )}[G_{n-1}]\in \mathcal {M}[G_{n-1}]$
. Moreover,
and
Summarizing, we have the following:
-
(1)
 $s_n=(s_0^n,\dot {s}_{[1,\omega )}^n),\dot {f},\mathscr {I},\varphi ,\mathcal {U},\dot {\mathbb {Q}}_{n}[G_{n-1}]*\tilde {\mathbb {P}}_{[n+1,\omega )}[G_{n-1}]\in \mathcal {M}[G_{n-1}]$
.
$s_n=(s_0^n,\dot {s}_{[1,\omega )}^n),\dot {f},\mathscr {I},\varphi ,\mathcal {U},\dot {\mathbb {Q}}_{n}[G_{n-1}]*\tilde {\mathbb {P}}_{[n+1,\omega )}[G_{n-1}]\in \mathcal {M}[G_{n-1}]$
. -
(2)
 $(\vec {t}_n,h_{n})\in \mathcal {M}[G_{n-1}]$
is a fine interpretation of
$(\vec {t}_n,h_{n})\in \mathcal {M}[G_{n-1}]$
is a fine interpretation of
 $\dot {f}$
below
$\dot {f}$
below
 $s_{n}$
.
$s_{n}$
. -
(3) Z is a pseudointersection of
 $\mathcal {M}[G_{n-1}]\cap \mathcal {U}$
and
$\mathcal {M}[G_{n-1}]\cap \mathcal {U}$
and
 $\varphi (h_n[Z])<m.$
$\varphi (h_n[Z])<m.$
Then we are in conditions to apply Lemma 5.5 for
![]() $n+1$
and
$n+1$
and
![]() $s_n$
taking the place of the condition p in the lemma. We get the following:
$s_n$
taking the place of the condition p in the lemma. We get the following:
-
(1) A
 $(\mathcal {M}[G_{n-1}],\dot {\mathbb {Q}}_{n}[G_{n-1}])$
-generic condition
$(\mathcal {M}[G_{n-1}],\dot {\mathbb {Q}}_{n}[G_{n-1}])$
-generic condition
 $q_{\mathcal {M}[G_{n-1}]}$
.
$q_{\mathcal {M}[G_{n-1}]}$
. -
(2) A
 $\dot {\mathbb {Q}}_{n}[G_{n-1}]$
-name
$\dot {\mathbb {Q}}_{n}[G_{n-1}]$
-name
 $\tilde {s}_{n+1}$
for a condition in
$\tilde {s}_{n+1}$
for a condition in $\tilde {\mathbb {P}}_{[n+1,\omega )}[G_{n-1}][\dot {G}_{\dot {\mathbb {Q}}_n[G_{n-1}]}]\cap \mathcal {M}[G_{n-1}][\dot {G}_{\dot {\mathbb {Q}}_n[G_{n-1}]}]$
.
$\tilde {\mathbb {P}}_{[n+1,\omega )}[G_{n-1}][\dot {G}_{\dot {\mathbb {Q}}_n[G_{n-1}]}]\cap \mathcal {M}[G_{n-1}][\dot {G}_{\dot {\mathbb {Q}}_n[G_{n-1}]}]$
. -
(3) A
 $\dot {\mathbb {Q}}_{n}[G_{n-1}]$
-name
$\dot {\mathbb {Q}}_{n}[G_{n-1}]$
-name
 $\tilde {h}_{n+1}$
for a finite to one function from
$\tilde {h}_{n+1}$
for a finite to one function from
 $\omega $
to
$\omega $
to
 $\omega $
.
$\omega $
. -
(4) A
 $\dot {\mathbb {Q}}_{n}[G_{n-1}]$
-name
$\dot {\mathbb {Q}}_{n}[G_{n-1}]$
-name
 for a sequence of conditions in
for a sequence of conditions in
 $\tilde {\mathbb {P}}_{[n+1,\omega )}[G_{n-1}][\dot {G}_{\dot {\mathbb {Q}}_n[G_{n-1}]}]$
.
$\tilde {\mathbb {P}}_{[n+1,\omega )}[G_{n-1}][\dot {G}_{\dot {\mathbb {Q}}_n[G_{n-1}]}]$
.
And such that the following hold:
-
(i)
 $q_{\mathcal {M}[G_{n-1}]}\leq s_n^0$
is a
$q_{\mathcal {M}[G_{n-1}]}\leq s_n^0$
is a
 $(\mathcal {M}[G_{n-1}],\dot {\mathbb {Q}}_n[G_{n-1}])$
-generic condition.
$(\mathcal {M}[G_{n-1}],\dot {\mathbb {Q}}_n[G_{n-1}])$
-generic condition. -
(ii)
 $q_{\mathcal {M}[G_{n-1}]}\Vdash ` `\tilde {s}_{n+1}\leq \dot {s}_{[1,\omega )}^{n}"$
and
$q_{\mathcal {M}[G_{n-1}]}\Vdash ` `\tilde {s}_{n+1}\leq \dot {s}_{[1,\omega )}^{n}"$
and
 $q_{\mathcal {M}}\Vdash ` `\tilde {s}_{n+1}\in \tilde {\mathbb {P}}_{[n+1,\omega )}[G_{n-1}] [\dot {G}_{\mathbb {Q}_n[G_{n-1}]}]\cap \mathcal {M}[\dot {G}_{n-1}][\dot {G}_{\mathbb {Q}_n[G_{n-1}]}]"$
.
$q_{\mathcal {M}}\Vdash ` `\tilde {s}_{n+1}\in \tilde {\mathbb {P}}_{[n+1,\omega )}[G_{n-1}] [\dot {G}_{\mathbb {Q}_n[G_{n-1}]}]\cap \mathcal {M}[\dot {G}_{n-1}][\dot {G}_{\mathbb {Q}_n[G_{n-1}]}]"$
. -
(iii)
 $q_{\mathcal {M}[G_{n-1}]}$
forces that
$q_{\mathcal {M}[G_{n-1}]}$
forces that
 is a fine interpretation of
is a fine interpretation of
 $\dot {f}$
below
$\dot {f}$
below
 $\tilde {s}_{n+1}$
, as well as
$\tilde {s}_{n+1}$
, as well as
 $\varphi (\tilde {h}_{n+1}[Z])<m$
.
$\varphi (\tilde {h}_{n+1}[Z])<m$
. -
(iv)
 $q_{\mathcal {M}[G_{n-1}]}\Vdash ` `\tilde {s}_{n+1}\Vdash ` `\dot {f}\upharpoonright (n+1)=\tilde {h}_{n+1}\upharpoonright (n+1)""$
.
$q_{\mathcal {M}[G_{n-1}]}\Vdash ` `\tilde {s}_{n+1}\Vdash ` `\dot {f}\upharpoonright (n+1)=\tilde {h}_{n+1}\upharpoonright (n+1)""$
.
All of these happen regarding
![]() $V[G_{n-1}]$
and
$V[G_{n-1}]$
and
![]() $\mathcal {M}[G_{n-1}]$
, and the construction was achieved by only assuming that
$\mathcal {M}[G_{n-1}]$
, and the construction was achieved by only assuming that
![]() $q_{n-1}\in G_{n-1}$
, and so everything above is forced by
$q_{n-1}\in G_{n-1}$
, and so everything above is forced by
![]() $q_{n-1}$
. Now, going back to V, we define the corresponding
$q_{n-1}$
. Now, going back to V, we define the corresponding
![]() $\mathbb {P}_{n}$
-names:
$\mathbb {P}_{n}$
-names:
-
 $\alpha $
)
$\alpha $
)
 $\dot {q}_n$
as a
$\dot {q}_n$
as a
 $\mathbb {P}_{n-1}$
-name for
$\mathbb {P}_{n-1}$
-name for
 $\dot {q}_{\mathcal {M}[G_{n-1}]}$
.
$\dot {q}_{\mathcal {M}[G_{n-1}]}$
. -
 $\beta $
)
$\beta $
)
 $\dot {s}_{n+1}$
as a
$\dot {s}_{n+1}$
as a
 $\mathbb {P}_{n-1}*\dot {\mathbb {Q}}_{n}$
-name for
$\mathbb {P}_{n-1}*\dot {\mathbb {Q}}_{n}$
-name for
 $\tilde {s}_{n+1}$
.
$\tilde {s}_{n+1}$
. -
 $\gamma $
)
$\gamma $
)
 $\dot {h}_{n+1}$
as a
$\dot {h}_{n+1}$
as a
 $\mathbb {P}_{n-1}*\dot {\mathbb {Q}}_{n}$
-name for
$\mathbb {P}_{n-1}*\dot {\mathbb {Q}}_{n}$
-name for
 $\tilde {h}_{n+1}$
.
$\tilde {h}_{n+1}$
. -
 $\delta $
)
$\delta $
)
 as a
as a
 $\mathbb {P}_{n-1}*\dot {\mathbb {Q}}_{n}$
-name for
$\mathbb {P}_{n-1}*\dot {\mathbb {Q}}_{n}$
-name for
 .
.
Finally, define
![]() $q_n=q_{n-1}\ ^{\frown } \dot {q}_n$
. Checking that these names are as required is routing as for case
$q_n=q_{n-1}\ ^{\frown } \dot {q}_n$
. Checking that these names are as required is routing as for case
![]() $n=1$
. This finishes the construction of the sequences, and therefore, the proof of Theorem 5.1.
$n=1$
. This finishes the construction of the sequences, and therefore, the proof of Theorem 5.1.
6 Answer to Question 1.4
Now we are ready to answer Question 1.4 stated in Section 1. We only state a remark that help us to prove a slightly more general result.
Lemma 6.1. Let
![]() $\mathscr {I}$
an analytic p-ideal. There is a summable ideal
$\mathscr {I}$
an analytic p-ideal. There is a summable ideal
![]() $\mathscr {J}$
such that
$\mathscr {J}$
such that
![]() $\mathscr {J}\subseteq \mathscr {I}$
.
$\mathscr {J}\subseteq \mathscr {I}$
.
Proof Let
![]() $\varphi $
be a lscsm which defines
$\varphi $
be a lscsm which defines
![]() $\mathscr {I}$
. Define
$\mathscr {I}$
. Define
![]() $Z=\{n\in \omega :\varphi (\{n\})=0\}$
. Note that since
$Z=\{n\in \omega :\varphi (\{n\})=0\}$
. Note that since
![]() $\varphi $
is a lscsm, the set Z is coinfinite. Now, for
$\varphi $
is a lscsm, the set Z is coinfinite. Now, for
![]() $n\notin Z$
, define
$n\notin Z$
, define
![]() $g(n)=\varphi (\{n\})$
, and for
$g(n)=\varphi (\{n\})$
, and for
![]() $n\in Z$
, define
$n\in Z$
, define
![]() $g(n)=1/2^n$
. The lower semicontinuity of
$g(n)=1/2^n$
. The lower semicontinuity of
![]() $\varphi $
implies that
$\varphi $
implies that
![]() $\mathscr {I}_g\subseteq \mathscr {I}$
.
$\mathscr {I}_g\subseteq \mathscr {I}$
.
It is clear that if
![]() $\mathscr {J}\subseteq \mathscr {I}$
are ideals, and
$\mathscr {J}\subseteq \mathscr {I}$
are ideals, and
![]() $\mathcal {U}$
is an
$\mathcal {U}$
is an
![]() $\mathscr {J}$
-ultrafilter, then
$\mathscr {J}$
-ultrafilter, then
![]() $\mathcal {U}$
is an
$\mathcal {U}$
is an
![]() $\mathscr {I}$
-ultrafilter as well.
$\mathscr {I}$
-ultrafilter as well.
Theorem 6.2. It is consistent that there is no rapid ultrafilter but given any family
![]() $\mathcal D$
of analytic p-ideals such that
$\mathcal D$
of analytic p-ideals such that
![]() $\lvert \mathcal D\rvert <\mathfrak {d}$
, there is an ultrafilter
$\lvert \mathcal D\rvert <\mathfrak {d}$
, there is an ultrafilter
![]() $\mathcal U$
which is an
$\mathcal U$
which is an
![]() $\mathscr {I}$
-ultrafilter for all
$\mathscr {I}$
-ultrafilter for all
![]() $\mathscr {I}\in \mathcal D$
.
$\mathscr {I}\in \mathcal D$
.
Proof First note that for all summable ideal
![]() $\mathscr {I}_g$
, it holds that
$\mathscr {I}_g$
, it holds that
![]() $\mathscr {I}_g=Fin(\varphi _g)=Exh(\varphi _g)$
, where
$\mathscr {I}_g=Fin(\varphi _g)=Exh(\varphi _g)$
, where
![]() $\varphi _g$
is the lscsm induced by
$\varphi _g$
is the lscsm induced by
![]() $g:\omega \to \mathbb {R}^+$
. The forcing
$g:\omega \to \mathbb {R}^+$
. The forcing
![]() $\mathbb {P}_{\omega _2}$
is an
$\mathbb {P}_{\omega _2}$
is an
![]() $\omega _2$
-length countable support iteration of the Rational Perfect set forcing over a model of
$\omega _2$
-length countable support iteration of the Rational Perfect set forcing over a model of
![]() $\mathsf {ZFC}+\mathsf {CH}$
. Theorem 4.8 states that Rational Perfect forcing preserves
$\mathsf {ZFC}+\mathsf {CH}$
. Theorem 4.8 states that Rational Perfect forcing preserves
![]() $(\mathscr {I},p)$
-points whenever
$(\mathscr {I},p)$
-points whenever
![]() $\mathscr {I}$
in an analytic p-ideal, and Theorem 5.1 makes sure that
$\mathscr {I}$
in an analytic p-ideal, and Theorem 5.1 makes sure that
![]() $(\mathscr {I},p)$
-points are preserved along the iteration whenever
$(\mathscr {I},p)$
-points are preserved along the iteration whenever
![]() $\mathscr {I}$
is an
$\mathscr {I}$
is an
![]() $F_{\sigma } \ p$
-ideal. Recall that in the Rational Perfect set model the dominating number is equal to
$F_{\sigma } \ p$
-ideal. Recall that in the Rational Perfect set model the dominating number is equal to
![]() $\omega _2$
. So let
$\omega _2$
. So let
![]() $\mathcal {D}$
be a family of analytic p-ideals such that
$\mathcal {D}$
be a family of analytic p-ideals such that
![]() $\vert \mathcal {D}\vert =\omega _1$
. Since every real appears before a stage of cofinality
$\vert \mathcal {D}\vert =\omega _1$
. Since every real appears before a stage of cofinality
![]() $\omega _1$
, it can be assumed that each ideal in
$\omega _1$
, it can be assumed that each ideal in
![]() $\mathcal {D}$
belongs to the ground model. By Lemma 6.1, for every
$\mathcal {D}$
belongs to the ground model. By Lemma 6.1, for every
![]() $\mathscr {I}\in \mathcal {D}$
there is a summable ideal
$\mathscr {I}\in \mathcal {D}$
there is a summable ideal
![]() $\mathscr {J}(\mathscr {I})$
such that
$\mathscr {J}(\mathscr {I})$
such that
![]() $\mathscr {J}(\mathscr {I})\subseteq \mathscr {I}$
. Define
$\mathscr {J}(\mathscr {I})\subseteq \mathscr {I}$
. Define
![]() $\mathcal {D}'=\{\mathscr {J}(\mathscr {I}):\mathscr {I}\in \mathcal {D}\}$
. Since these ideals are from the ground model, there is an ultrafilter
$\mathcal {D}'=\{\mathscr {J}(\mathscr {I}):\mathscr {I}\in \mathcal {D}\}$
. Since these ideals are from the ground model, there is an ultrafilter
![]() $\mathcal {U}$
that is an
$\mathcal {U}$
that is an
![]() $(\mathscr {I},p)$
-point for every ideal
$(\mathscr {I},p)$
-point for every ideal
![]() $\mathscr {I}\in \mathcal {D}'$
(for example,
$\mathscr {I}\in \mathcal {D}'$
(for example,
![]() $\mathcal {U}$
may be a Ramsey ultrafilter). This ultrafilter remains as an
$\mathcal {U}$
may be a Ramsey ultrafilter). This ultrafilter remains as an
![]() $(\mathscr {I},p)$
-point for every
$(\mathscr {I},p)$
-point for every
![]() $\mathscr {I}\in \mathcal {D}'$
in the forcing extension by
$\mathscr {I}\in \mathcal {D}'$
in the forcing extension by
![]() $\mathbb {P}_{\omega _2}$
, which implies that
$\mathbb {P}_{\omega _2}$
, which implies that
![]() $\mathcal {U}$
is an
$\mathcal {U}$
is an
![]() $(\mathscr {I},p)$
-point for any
$(\mathscr {I},p)$
-point for any
![]() $\mathscr {I}\in \mathcal {D}$
.
$\mathscr {I}\in \mathcal {D}$
.
7 Final remarks
Let us recall that T. Bartoszyński and S. Shelah have proved that in the Rational Perfect set model, the Hausdorff ultrafilters are dense in the Rudin–Blass ordering (see [Reference Bartoszyński and Shelah2]).
Theorem 7.1 (Bartoszyński and Shelah, see [Reference Bartoszyński and Shelah2]).
In the Rational Perfect set model, Hausdorff ultrafilters are dense in the Rudin–Blass ordering.
Theorem 6.2 implies the same fact for a broader class of ideals. First let us recall the Near Coherence of Filters principle:
Definition 7.2 (Near Coherence of Filters principle (NCF); Blass, see [Reference Blass4]).
Let
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $\mathcal {V}$
be two ultrafilters on
$\mathcal {V}$
be two ultrafilters on
![]() $\omega $
. Then there is a finite to one function
$\omega $
. Then there is a finite to one function
![]() $f:\omega \to \omega $
such that
$f:\omega \to \omega $
such that
![]() $f(\mathcal {U})=f(\mathcal {V})$
.
$f(\mathcal {U})=f(\mathcal {V})$
.
Theorem 7.3 (Blass and Shelah, see [Reference Blass and Shelah6]).
The Near Coherence of Filters holds in the Rational Perfect set model.
Let us work in the Rational Perfect set model. Let
![]() $\mathscr {I}$
be any analytic p-ideal, and apply Theorem 6.2 to the family
$\mathscr {I}$
be any analytic p-ideal, and apply Theorem 6.2 to the family
![]() $\mathcal {D}=\{\mathscr {I}\}$
to obtain an
$\mathcal {D}=\{\mathscr {I}\}$
to obtain an
![]() $\mathscr {I}$
-ultrafilter
$\mathscr {I}$
-ultrafilter
![]() $\mathcal {U}$
. Now let
$\mathcal {U}$
. Now let
![]() $\mathcal {V}$
be an arbitrary ultrafilter on
$\mathcal {V}$
be an arbitrary ultrafilter on
![]() $\omega $
. By Theorem 7.3, there is a finite to one function
$\omega $
. By Theorem 7.3, there is a finite to one function
![]() $f\in \omega ^{\omega }$
such that
$f\in \omega ^{\omega }$
such that
![]() $f(\mathcal {U})=f(\mathcal {V})$
. Since
$f(\mathcal {U})=f(\mathcal {V})$
. Since
![]() $f(\mathcal {U})$
is a
$f(\mathcal {U})$
is a
![]() $\mathscr {I}$
-ultrafilter and
$\mathscr {I}$
-ultrafilter and
![]() $f(\mathcal {U})=f(\mathcal {V})\leq _{RB}\mathcal {V}$
, we have found an
$f(\mathcal {U})=f(\mathcal {V})\leq _{RB}\mathcal {V}$
, we have found an
![]() $\mathscr {I}$
-ultrafilter below
$\mathscr {I}$
-ultrafilter below
![]() $\mathcal {V}$
. We have proved the following:
$\mathcal {V}$
. We have proved the following:
Corollary 7.4. It is relatively consistent with
![]() $\mathsf {ZFC}$
that for any analytic p-ideal,
$\mathsf {ZFC}$
that for any analytic p-ideal,
![]() $\mathscr {I}$
-ultrafilters are dense in the Rudin–Blass ordering. Actually, this holds in the Rational Perfect set model.
$\mathscr {I}$
-ultrafilters are dense in the Rudin–Blass ordering. Actually, this holds in the Rational Perfect set model.
Also, recall that C. Laflamme and J. Zhu, in their article The Rudin Blass ordering of ultrafilters from 1998 (see [Reference Laflamme and Zhu11]), have proved in
![]() $\mathsf {ZFC}$
that there is an ultrafilter
$\mathsf {ZFC}$
that there is an ultrafilter
![]() $\mathcal {U}$
with no Rudin–Blass predecessors which are rapid. In particular, no predecessor of
$\mathcal {U}$
with no Rudin–Blass predecessors which are rapid. In particular, no predecessor of
![]() $\mathcal {U}$
is a q-point, equivalently, a weak
$\mathcal {U}$
is a q-point, equivalently, a weak
![]() $\mathcal {ED}_{fin}$
-ultrafilter. Corollary 7.4 implies that it is not possible to prove the same for
$\mathcal {ED}_{fin}$
-ultrafilter. Corollary 7.4 implies that it is not possible to prove the same for
![]() $\mathscr {I}$
-ultrafilters whenever
$\mathscr {I}$
-ultrafilters whenever
![]() $\mathscr {I}$
is an analytic p-ideal.
$\mathscr {I}$
is an analytic p-ideal.
Recall that given two ideals
![]() $\mathscr {I}$
and
$\mathscr {I}$
and
![]() $\mathscr {J}$
on
$\mathscr {J}$
on
![]() $\omega $
, we say that
$\omega $
, we say that
![]() $\mathscr {I}$
is Katětov below
$\mathscr {I}$
is Katětov below
![]() $\mathscr {J}$
, denoted by
$\mathscr {J}$
, denoted by
![]() $\mathscr {I}\leq _K\mathscr {J}$
, if there is a function
$\mathscr {I}\leq _K\mathscr {J}$
, if there is a function
![]() $f:\omega \to \omega $
such that for all
$f:\omega \to \omega $
such that for all
![]() $A\in \mathscr {I}$
,
$A\in \mathscr {I}$
,
![]() $f^{-1}[A]\in \mathscr {J}$
. If the function f is required to be finite to one, then we say that
$f^{-1}[A]\in \mathscr {J}$
. If the function f is required to be finite to one, then we say that
![]() $\mathscr {I}$
is Katětov–Blass below
$\mathscr {I}$
is Katětov–Blass below
![]() $\mathscr {J}$
, and it is denoted by
$\mathscr {J}$
, and it is denoted by
![]() $\mathscr {I}\leq _{KB}\mathscr {J}$
. For a given ideal
$\mathscr {I}\leq _{KB}\mathscr {J}$
. For a given ideal
![]() $\mathscr {I}$
and an ultrafilter
$\mathscr {I}$
and an ultrafilter
![]() $\mathcal {U}$
, it is easily seen that
$\mathcal {U}$
, it is easily seen that
![]() $\mathcal {U}$
is an
$\mathcal {U}$
is an
![]() $\mathscr {I}$
-ultrafilter if and only if
$\mathscr {I}$
-ultrafilter if and only if
![]() $\mathscr {I}\nleq _K\mathcal {U}^*$
. Similarly,
$\mathscr {I}\nleq _K\mathcal {U}^*$
. Similarly,
![]() $\mathcal {U}$
is a weak
$\mathcal {U}$
is a weak
![]() $\mathscr {I}$
-ultrafilter if and only if
$\mathscr {I}$
-ultrafilter if and only if
![]() $\mathscr {I}\nleq _{KB}\mathcal {U}^*$
. Using this terminology, Laflamme and Zhu’s theorem can be restated as follows:
$\mathscr {I}\nleq _{KB}\mathcal {U}^*$
. Using this terminology, Laflamme and Zhu’s theorem can be restated as follows:
Theorem 7.5 (Laflamme and Zhu, see [Reference Laflamme and Zhu11]).
There exists an ultrafilter
![]() $\mathcal {U}$
such that for all finite to one
$\mathcal {U}$
such that for all finite to one
![]() $f\in \omega ^{\omega }$
,
$f\in \omega ^{\omega }$
,
![]() $\mathcal {ED}_{fin}\leq _{KB}f(\mathcal {U})^*$
.
$\mathcal {ED}_{fin}\leq _{KB}f(\mathcal {U})^*$
.
Thus, it follows trivially that for any Borel ideal
![]() $\mathscr {I}\leq _{KB}\mathcal {ED}_{fin}$
, there is an ultrafilter for which any Rudin–Blass predecessor
$\mathscr {I}\leq _{KB}\mathcal {ED}_{fin}$
, there is an ultrafilter for which any Rudin–Blass predecessor
![]() $\mathcal {V}\leq _{RB}\mathcal {U}$
, its dual ideal is Katětov–Blass above
$\mathcal {V}\leq _{RB}\mathcal {U}$
, its dual ideal is Katětov–Blass above
![]() $\mathscr {I}$
, that is
$\mathscr {I}$
, that is
![]() $\mathscr {I}\leq _{KB}\mathcal {V}^*$
. However, we do not know of a Borel ideal
$\mathscr {I}\leq _{KB}\mathcal {V}^*$
. However, we do not know of a Borel ideal
![]() $\mathscr {I}\nleq _{KB}\mathcal {ED}_{fin}$
having this property.
$\mathscr {I}\nleq _{KB}\mathcal {ED}_{fin}$
having this property.
Definition 7.6. Let
![]() $\mathscr {I}$
be a tall ideal on
$\mathscr {I}$
be a tall ideal on
![]() $\omega $
. We say that
$\omega $
. We say that
![]() $\mathscr {I}$
is Laflamme–Zhu if there is an ultrafilter
$\mathscr {I}$
is Laflamme–Zhu if there is an ultrafilter
![]() $\mathcal {U}$
all of whose Rudin–Blass predecessors are such that its dual ideal is Katětov–Blass above of
$\mathcal {U}$
all of whose Rudin–Blass predecessors are such that its dual ideal is Katětov–Blass above of
![]() $\mathscr {I}$
. We say that
$\mathscr {I}$
. We say that
![]() $\mathscr {I}$
is trivially Laflamme–Zhu if
$\mathscr {I}$
is trivially Laflamme–Zhu if
![]() $\mathscr {I}<_{KB}\mathcal {ED}_{fin}$
.
$\mathscr {I}<_{KB}\mathcal {ED}_{fin}$
.
The previous remarks lead us to ask the following:
Question 7.7. Does there exist a Borel or analytic tall ideal other than
![]() $\mathcal {ED}_{fin}$
which is non-trivially Laflamme–Zhu?
$\mathcal {ED}_{fin}$
which is non-trivially Laflamme–Zhu?
Question 7.8. Is there a critical ideal
![]() $\mathscr {I}$
for the Borel (analytic) Laflamme–Zhu ideals, i.e., such that any ideal
$\mathscr {I}$
for the Borel (analytic) Laflamme–Zhu ideals, i.e., such that any ideal
![]() $\mathscr {J}$
is Laflamme–Zhu if and only if
$\mathscr {J}$
is Laflamme–Zhu if and only if
![]() $\mathscr {J}\leq _{KB}\mathscr {I}$
?
$\mathscr {J}\leq _{KB}\mathscr {I}$
?
Question 7.9. In case there is an analytic ideal
![]() $\mathscr {I}\nleq _{KB}\mathcal {ED}_{fin}$
which is Laflamme–Zhu, let
$\mathscr {I}\nleq _{KB}\mathcal {ED}_{fin}$
which is Laflamme–Zhu, let
![]() $\mathbf {LZ}_{Borel}$
and
$\mathbf {LZ}_{Borel}$
and
![]() $\mathbf {LZ}_{Analytic}$
be the families of all Borel and analytic ideals which are Laflamme–Zhu, respectively. What is the structure of the Katětov–Blass order restricted to such classes?
$\mathbf {LZ}_{Analytic}$
be the families of all Borel and analytic ideals which are Laflamme–Zhu, respectively. What is the structure of the Katětov–Blass order restricted to such classes?
In the case of an affirmative answer to Question 7.7
, such ideal can not be Katětov–Blass above the ideal
![]() $\mathsf {conv}$
generated by convergent sequences of rationals in
$\mathsf {conv}$
generated by convergent sequences of rationals in
![]() $\mathbb {Q}\cap [0,1]$
, since p-points are characterized as the
$\mathbb {Q}\cap [0,1]$
, since p-points are characterized as the
![]() $\mathsf {conv}$
-ultrafilters. Also, by Corollary 7.4, such an ideal can not be an analytic p-ideal. In particular it can not be a summable ideal. In [Reference Hrušák and Meza-Alcántara9] it has been proved that Hausdorff ultrafilters are exactly the
$\mathsf {conv}$
-ultrafilters. Also, by Corollary 7.4, such an ideal can not be an analytic p-ideal. In particular it can not be a summable ideal. In [Reference Hrušák and Meza-Alcántara9] it has been proved that Hausdorff ultrafilters are exactly the
![]() $\mathcal {G}_{fc}$
-ultrafilters, which together with Theorem 7.1 imply that any Lafflame–Zhu ideal can not be Katětov–Blass above the ideal
$\mathcal {G}_{fc}$
-ultrafilters, which together with Theorem 7.1 imply that any Lafflame–Zhu ideal can not be Katětov–Blass above the ideal
![]() $\mathcal {G}_{fc}$
, the ideal on
$\mathcal {G}_{fc}$
, the ideal on
![]() $[\omega ]^2$
of graphs with finite chromatic number.
$[\omega ]^2$
of graphs with finite chromatic number.