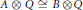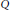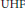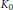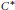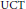Research Article
The Equivariant Grothendieck Groups of the Russell-Koras Threefolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-32
-
- Article
-
- You have access
- Export citation
Merit Factors of Polynomials Formed by Jacobi Symbols
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-50
-
- Article
-
- You have access
- Export citation
A Continuous Field of Projectionless C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 51-72
-
- Article
-
- You have access
- Export citation
Stratification Theory from the Weighted Point of View
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 73-97
-
- Article
-
- You have access
- Export citation
On the Curves Associated to Certain Rings of Automorphic Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 98-121
-
- Article
-
- You have access
- Export citation
A Truncated Integral of the Poisson Summation Formula
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 122-160
-
- Article
-
- You have access
- Export citation
Classification of Simple Tracially AF C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 161-194
-
- Article
-
- You have access
- Export citation
On the Steinberg Map and Steinberg Cross-Section for a Symmetrizable Indefinite Kac-Moody Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 195-211
-
- Article
-
- You have access
- Export citation
Group Actions and Codes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 212-224
-
- Article
-
- You have access
- Export citation