Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T21:20:23.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Merit Factors of Polynomials Formed by Jacobi Symbols

Published online by Cambridge University Press:  20 November 2018

Peter Borwein  and
Kwok-Kwong Stephen Choi
Peter Borwein
Affiliation:
Department of Mathematics and Statistics, Simon Fraser University, Burnaby, BC, V5A 1S6
Kwok-Kwong Stephen Choi
Affiliation:
Department of Mathematics, The University of Hong Kong, Pokfulam Road, Hong Kong
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

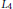We give explicit formulas for the ${{L}_{4}}$ norm (or equivalently for the merit factors) of various sequences of polynomials related to the polynomials

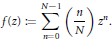$$f\left( z \right):=\,\sum\limits_{n=0}^{N-1}{\left( \frac{n}{N} \right){{z}^{n}}.}$$

and

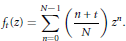$${{f}_{t}}(z)\,=\,\sum\limits_{n=0}^{N-1}{\left( \frac{n+t}{N} \right){{z}^{n}}.}$$

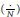where $\left( \frac{.}{N} \right)$ is the Jacobi symbol.

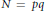Two cases of particular interest are when $N\,=\,pq$ is a product of two primes and 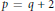$p\,=\,q\,+\,2$ or 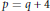$p\,=\,q\,+\,4$. This extends work of Høholdt, Jensen and Jensen and of the authors.

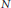This study arises from a number of conjectures of Erdős, Littlewood and others that concern the norms of polynomials with −1, 1 coefficients on the disc. The current best examples are of the above form when $N$ is prime and it is natural to see what happens for composite 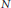$N$.

Keywords

11J5411B8312-04Character polynomialClass Number−1, 1 coefficientsMerit factorFekete polynomialsTuryn PolynomialsLittlewood polynomialsTwin PrimesJacobi Symbols
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 1 , 01 February 2001 , pp. 33 - 50
Copyright
Copyright © Canadian Mathematical Society 2001

References

[A-80] Apostol, T. M., Introduction to Analytic Number Theory. Springer-Verlag, Berlin, 1980.Google Scholar
[B-95] Beck, J., Flat polynomials on the unit circle—note on a problem of Littlewood. Bull. London Math. Soc. 23(1991), 269–27.Google Scholar
[BEW-98] Berndt, B. C., Evans, R. J. and S. Williams, K., Gauss and Jacobi Sums. In: Canadian Mathematical Society Series of Monographs and Advanced Texts, Wiley-Interscience, New York, 1998.Google Scholar
[BC-98] Borwein, P. and Choi, K. K., Explicit Merit Factor Formulae for Fekete and Turyn Polynomials. Under submission.Google Scholar
[BC-99] Borwein, P. and Choi, K. K., Merit Factors of Character Polynomials. J. LondonMath. Soc., to appear.Google Scholar
[E-57] Erdős, P., Some unsolved problems. Michigan Math. J. 4(1957), 291–300.Google Scholar
[E-62] Erdős, P., An inequality for the maximum of trigonometric polynomials. Ann. Polon. Math. 12(1962), 151–154.Google Scholar
[CGP-98] Conrey, B., Granville, A. and Poonen, B., Zeros of Fekete polynomials. In press.Google Scholar
[G-83] Golay, M. J., The merit factor of Legendre sequences. IEEE Trans. Inform. Theory 29(1983), 934–936.Google Scholar
[HJ-88] Høholdt, T. and Jensen, H., Determination of the merit factor of Legendre sequences. IEEE Trans. Inform. Theory 34(1988), 161–164.Google Scholar
[HJJ-91] Høholdt, T., Jensen, H. and Jensen, J., The merit factor of binary sequences related to difference sets. IEEE Trans. Inform. Theory 37(1991), 617–626.Google Scholar
[K-80] Kahane, J-P., Sur les polynômes à coefficients unimodulaires. Bull. LondonMath. Soc. 12(1980), 321–342.Google Scholar
[L-68] Littlewood, J. E., Some Problems in Real and Complex Analysis. Heath Mathematical Monographs, Lexington, Massachusetts, 1968.Google Scholar
[M-94] Montgomery, H. L., Ten Lectures on the Interface Between Analytic Number Theory and Harmonic Analysis. CBMS 84, Amer.Math. Soc., Providence, RI, 1994.Google Scholar
[NB-90] Newman, D. J. and Byrnes, J. S., The L4 norm of a polynomial with coefficients ±1. Amer. Math.Monthly 97(1990), 42–45.Google Scholar
[S-90] Saffari, B., Barker sequences and Littlewood's “two-sided conjectures” on polynomials with ±1 coefficients. Séminaire d’Analyse Harmonique. Année 1989/90, Univ. Paris XI, Orsay, 1990, 139–151.Google Scholar