Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-26T01:16:52.612Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of Simple Tracially AF C*-Algebras

Published online by Cambridge University Press:  20 November 2018

Huaxin Lin
Huaxin Lin*
Affiliation:
Department of Mathematics, East China Normal University, Shanghai, China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that pre-classifiable (see 3.1) simple nuclear tracially 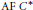$\text{AF}\,\,{{C}^{*}}$-algebras 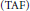$\left( \text{TAF} \right)$ are classified by their 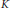$K$-theory. As a consequence all simple, locally 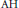$\text{AH}$ and 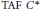$\text{TAF}\,\,\,{{C}^{*}}$-algebras are in fact 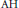$\text{AH}$ algebras (it is known that there are locally 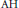$\text{AH}$ algebras that are not 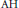$\text{AH}$). We also prove the following Rationalization Theorem. Let $A$ and 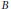$B$ be two unital separable nuclear simple $\text{TAF}\,\,\,{{C}^{*}}$-algebras with unique normalized traces satisfying the Universal Coefficient Theorem. 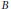If $A$ and $B$ have the same (ordered and scaled) $K$-theory and 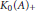${{K}_{0}}{{\left( A \right)}_{+}}$ is locally finitely generated, then 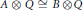$A\,\otimes \,Q\,\cong \,B\,\otimes \,Q$, where $Q$ is the 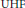$\text{UHF}$-algebra with the rational 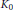${{K}_{0}}$. Classification results (with restriction on 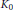${{K}_{0}}$ - theory) for the above 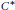${{C}^{*}}$-algebras are also obtained. 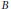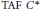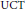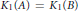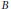For example, we show that, if $A$ and $B$ are unital nuclear separable simple $\text{TAF}\,\,\,{{C}^{*}}$-algebras with the unique normalized trace satisfying the $\text{UCT}$ and with ${{K}_{1}}\left( A \right)\,=\,{{K}_{1}}\left( B \right)$, and $A$ and $B$ have the same rational (scaled ordered) 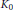${{K}_{0}}$, then 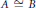$A\,\cong \,B$. Similar results are also obtained for some cases in which 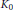${{K}_{0}}$ is non-divisible such as 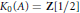${{K}_{0}}\left( A \right)\,=\,\mathbf{Z}\left[ 1/2 \right]$.

Keywords

46L0546L35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 1 , 01 February 2001 , pp. 161 - 194
Copyright
Copyright © Canadian Mathematical Society 2001

References

[Bl] Blackadar, B., K-Theory for Operator Algebras. Springer-Verlag, New York, 1986.Google Scholar
[BH] Blackadar, B. and Handelman, D., Dimension functions and traces on C*-algebras. J. Funct. Anal. 45(1982), 297–340.Google Scholar
[BKR] B. Blackadar, Kumjian, A. and Rørdam, M., Approximately central matrix units and the structure of noncommutative tori. K-theory 6(1992), 267–284.Google Scholar
[BK1] Blackadar, B. and Kirchberg, E., Generalized inductive limits of finite-dimensional C*-algebras. Math. Ann. 307(1997), 343–380.Google Scholar
[BK2] Blackadar, B. and Kirchberg, E., Inner quasidiagonality and strong NF algebras. Preprint.Google Scholar
[Br] Brown, L. G., Extensions and the structure of C*-algebras. Istituto Nazionale di AltaMathematica, Symposia Mathematica 20(1976), 539–566.Google Scholar
[BP] Brown, L. G. and Pedersen, G. K., C*-algebras of real rank zero. J. Funct. Anal. 99(1991), 131–149.Google Scholar
[CE1] Choi, M-D. and Effros, E., The completely positive lifting problem for C*-algebras. Ann. Math. 104(1976), 585–609.Google Scholar
[D1] Dadarlat, M., Reduction to dimension three of local spectra of real rank zero C*-algebras. J. Reine Angew.Math. 460(1995), 189–212.Google Scholar
[D2] Dadarlat, M., Approximately unitarily equivalent morphisms and inductive limit C*-algebras. K-theory 9(1995), 117–137.Google Scholar
[D3] Dadarlat, M., Nonnuclear subalgebras of AF algebras. Preprint.Google Scholar
[D4] Dadarlat, M., On the approximation of quasidiagonal C*-algebras. Preprint.Google Scholar
[D5] Dadarlat, M., Residually finite dimensional C*-algebras. Preprint.Google Scholar
[DE] Dadarlat, M. and Eilers, S., Approximate homogeneity is not a local property. Preprint, 1997.Google Scholar
[DL1] Dadarlat, M. and Loring, T., K-homology, asymptotic representations, and unsuspended E-theory. J. Funct. Anal. 126(1994), 367–383.Google Scholar
[DL2] Dadarlat, M. and Loring, T., A universal multi-coefficient theorem for the Kasparov groups. Duke J. Math. 84(1996), 355–377.Google Scholar
[Ell1] Elliott, G. A., On the classification of C*-algebras of real rank zero. J. Reine Angew.Math. 443(1993), 179–219.Google Scholar
[Ell2] Elliott, G. A., The classification problem for amenable C*-algebras. Proc. ICM ‘94 (Zurich, Switzerland), Birkhauser, Basel, 1995, 922–932.Google Scholar
[EE] Elliott, G. A. and Evans, D. E., The structure of irrational rotationC*-algebras. Ann.Math. 138(1993), 477–501.Google Scholar
[EG] Elliott, G. A. and Gong, G., On the classification of C*-algebras of real rank zero, II. Ann. Math. 144(1996), 497–610.Google Scholar
[EGL] Elliott, G. A., Gong, G. and Li, L., On the classification of simple inductive limit C*-algebras, II: The isomorphism theorem. Preprint.Google Scholar
[EGLP] Elliott, G. A., G. Gong, Lin, H. and Pasnicu, C., Abelian C*-subalgebras of C*-algebras of real rank zero and inductive limit C*-algebras. DukeMath. J. 85(1996), 511–554.Google Scholar
[EHS] Effros, E., D. Handelman and Shen, C. L., Dimension groups and their affine representations. Amer. J. Math. 102(1980), 385–407.Google Scholar
[G1] Gong, G., On the inductive limits of matrix algebras over higher dimensional spaces, I and II. Math. Scand. 80(1997) 40–55 and 56–100.Google Scholar
[G2] Gong, G., On the classification of simple inductive limit C*-algebras, I; The reduction theorem. Preprint.Google Scholar
[H] Higson, N., A characterization of KK-theory. Pacific J. Math. 126(1987), 253–276.Google Scholar
[Li] Li, L., C*-algebra homomorphisms and K-theory. K-theory 18(1999), 157–172.Google Scholar
[Ln1] Lin, H., Skeleton C*-subalgebras. Canad. J. Math. 44(1992), 324–341.Google Scholar
[Ln2] Lin, H., Almost multiplicative morphisms and some applications. J. Operator Theory 37(1997), 121–154.Google Scholar
[Ln3] Lin, H., Extensions of C(X)by simple C*-algebras of real rank zero. Amer. J. Math. 119(1997), 1263–1289.Google Scholar
[Ln4] Lin, H., Classification of simple C*-algebras with unique traces. Amer. J. Math. 119(1997), 1263–1289.Google Scholar
[Ln5] Lin, H., Stable approximate unitarily equivalence of homomorphisms. J. Operator Theory, to appear.Google Scholar
[Ln6] Lin, H., Tracially AF C*-algebras. Trans. Amer.Math. Soc., to appear.Google Scholar
[Ln7] Lin, H., Locally type I simple tracially AF C*-algebras. Preprint.Google Scholar
[Pa] Paulsen, V. I., Completely bounded maps and dilations. Pitnam Research Notes in Math. 146, Sci. Tech. Harlow, 1986.Google Scholar
[Pd] Pedersen, G. K., C*-algebras and their Automorphism Groups. Academic Press, London/New York/San Francisco, 1979.Google Scholar
[Po] Popa, S., On local finite dimensional approximation of C*-algebras. Pacific J. Math. 181(1997), 141–158.Google Scholar
[Ph] Phillips, N. C., A classification theorem for nuclear purely infinite simple C*-algebras. Preprint.Google Scholar
[R] Rørdam, M., Classification of certain infinite simple C*-algebras. J. Funct. Anal. 131(1995), 415–458.Google Scholar
[RS] Rosenberg, J. and Schochet, C., The Kunneth theorem and the universal Coefficient theorem for Kasparov's generalized functor. DukeMath. J. 55(1987), 431–474.Google Scholar
[Sc1] Schochet, C., Topological methods for C*-algebras III: axiomatic homology. Pacific J. Math. 114(1984), 399–445.Google Scholar
[Sc2] Schochet, C., Topological methods for C*-algebras IV: mod p homology. Pacific J. Math. 114(1984), 447–468.Google Scholar
[Th] Thomsen, K., On isomorphisms of inductive limits of C*-algebras. Proc. Amer. Math. Soc. 113(1991), 947–953.Google Scholar
[Zh1] Zhang, S., C*-algebras with real rank zero and the internal structure of their corona and multiplier algebras, I. Pacific J. Math. 155(1992), 169–197.Google Scholar
[Zh2] Zhang, S., A property of purely infinite simple C*-algebras. Proc. Amer. Math. Soc. 109(1990), 717–720.Google Scholar
[Zh3] Zhang, S., Matricial structure and homotopy type of simple C*-algebras with real rank zero. J. Operator Theory 26(1991), 283–312.Google Scholar