We study the automorphism group of the algebraic closure of a substructure A of a pseudo-finite field F. We show that the behavior of this group, even when A is large, depends essentially on the roots of unity in F. For almost all completions of the theory of pseudofinite fields, we show that over A, algebraic closure agrees with definable closure, as soon as A contains the relative algebraic closure of the prime field.

We show, for each computable ordinal α and degree a > 0(α), the existence of a torsion-free abelian group with proper αth jump degree a.

Assuming 2ℵ0 = ℵ1 and 2ℵ1 = ℵ2, we build a partial order that forces the existence of a well-order of H(ω2) lightface definable over ⟨H(ω1), ∈⟩ and that preserves cardinal exponentiation and cofinalities.

This paper studies homogeneously Suslin (hom) sets of reals in tame mice. The following results are established: In 0¶ the hom sets are precisely the sets. In Mn every hom set is correctly , and (δ + 1)-universally Baire where δ is the least Woodin. In Mω, every hom set is <λ-hom, where λ is the supremum of the Woodins.

We construct a fibered dimension function in some topological differential fields.

A structure 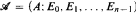is an n-grid if each Ei, is an equivalence relation on A and whenever X and Y are equivalence classes of, respectively, distinct Ei, and Ej, then X ∩ Y is finite. A coloring χ: A → n is acceptable if whenever X is an equivalence class of Ei, then {x ∈ X: χ(x) = i} is finite. If B is any set, then the n-cube Bn = (Bn; E0, …, En−1) is considered as an n-grid, where the equivalence classes of Ei are the lines parallel to the i-th coordinate axis. Kuratowski [9], generalizing the n = 3 case proved by Sierpihski [17], proved that ℝn has an acceptable coloring iff 2ℵ0 ≤ ℵn−2. The main result is: if 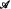is a semialgebraic (i.e., first-order definable in the field of reals) n-grid, then the following are equivalent: (1) if 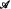embeds all finite n-cubes, then 2ℵ0 ≤ ℵn−2: (2) if 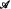embeds ℝn, then 2ℵ0 ≤ ℵn−2; (3) 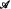has an acceptable coloring.

We show that the theory of the local structure of the enumeration degrees is computably isomorphic to the theory of first order arithmetic. We introduce a novel coding method, using the notion of a -pair, to code a large class of countable relations.

We work in , the untyped λ-calculus in which all unsolvables are identified. We resolve a conjecture of Barendregt asserting that the range of a definable map is either infinite or a singleton. This is refuted by constructing a λ-term Ξ such that ΞM = ΞI ⇔ ΞM ≠ ΞΩ. The construction generalizes to ranges of any finite size, and to some other sensible lambda theories.

In this article we establish the undecidability of representability and of finite representability as algebras of binary relations in a wide range of signatures. In particular, representability and finite representability are undecidable for Boolean monoids and lattice ordered monoids, while representability is undecidable for Jónsson's relation algebra. We also establish a number of undecidability results for representability as algebras of injective functions.

We prove that a Kueker theory with infinite dcl(∅) does not have the strict order property and that strongly minimal types are dense: any non-algebraic formula is contained in a strongly minimal type.

We consider VC-minimal theories admitting unpackable generating families, and show that in such theories, forking of formulae over a model M is equivalent to containment in global types definable over M, generalizing a result of Dolich on o-minimal theories in [4].

In this paper, we propose a weak regularity principle which is similar to both weak König's lemma and Ramsey's theorem. We begin by studying the computational strength of this principle in the context of reverse mathematics. We then analyze different ways of generalizing this principle.

We show that strongly compact cardinals and MM are sensitive to λ-closed forcings for arbitrarily large λ. This is done by adding ‘regressive’ λ-Kurepa trees in either case. We argue that the destruction of regressive Kurepa trees requires a non-standard application of MM. As a corollary, we find a consistent example of an ω2-closed poset that is not forcing equivalent to any ω2-directed-closed poset.

In this paper we describe the well-founded initial segment of the free Heyting algebra α on finitely many, α, generators. We give a complete classification of initial sublattices of 2 isomorphic to 1 (called ‘low ladders’), and prove that for 2 ≤ α < ω, the height of the well-founded initial segment of α is ω2.

We construct a Galois connection between closure and interior operators on a given set. All arguments are intuitionistically valid. Our construction is an intuitionistic version of the classical correspondence between closure and interior operators via complement.

We prove that if holds for a singular cardinal μ, then any collection of fewer than cf(μ) stationary subsets of μ+ must reflect simultaneously.