Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schlutzenberg, Farmer
2023.
The definability of E in self-iterable mice.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 2,
p.
103208.
SARGSYAN, GRIGOR
2023.
NEGATIVE RESULTS ON PRECIPITOUS IDEALS ON .
The Journal of Symbolic Logic,
Vol. 88,
Issue. 2,
p.
490.


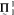 sets. In
sets. In 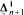 , and (
, and (