For each real number 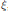 $\xi$, let
$\xi$, let 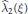 $\widehat{{{\lambda }_{2}}}\left( \xi \right)$ denote the supremum of all real numbers
$\widehat{{{\lambda }_{2}}}\left( \xi \right)$ denote the supremum of all real numbers  $\text{ }\!\!\lambda\!\!\text{ }$
such that, for each sufficiently large
$\text{ }\!\!\lambda\!\!\text{ }$
such that, for each sufficiently large  $X$
, the inequalities
$X$
, the inequalities 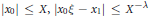 $\left| {{x}_{0}} \right|\,\le \,X,\,\left| {{x}_{0}}\xi \,-\,{{x}_{1}} \right|\,\le \,{{X}^{-\lambda \text{ }}}$ and
$\left| {{x}_{0}} \right|\,\le \,X,\,\left| {{x}_{0}}\xi \,-\,{{x}_{1}} \right|\,\le \,{{X}^{-\lambda \text{ }}}$ and 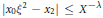 $\left| {{x}_{0}}{{\xi }^{2}}\,-\,{{x}_{2}} \right|\,\le \,{{X}^{-\lambda \text{ }}}$ admit a solution in integers
$\left| {{x}_{0}}{{\xi }^{2}}\,-\,{{x}_{2}} \right|\,\le \,{{X}^{-\lambda \text{ }}}$ admit a solution in integers 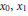 ${{x}_{0}},\,{{x}_{1}}$ and
${{x}_{0}},\,{{x}_{1}}$ and  ${{x}_{2}}$ not all zero, and let
${{x}_{2}}$ not all zero, and let 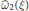 $\widehat{{{\omega }_{2}}}\left( \xi \right)$ denote the supremum of all real numbers
$\widehat{{{\omega }_{2}}}\left( \xi \right)$ denote the supremum of all real numbers  $\omega $ such that, for each sufficiently large
$\omega $ such that, for each sufficiently large  $X$, the dual inequalities
$X$, the dual inequalities 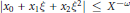 $\left| {{x}_{0}}\,+\,{{x}_{1}}\xi \,+\,{{x}_{2}}{{\xi }^{2}} \right|\,\le \,{{X}^{-\omega }}$,
$\left| {{x}_{0}}\,+\,{{x}_{1}}\xi \,+\,{{x}_{2}}{{\xi }^{2}} \right|\,\le \,{{X}^{-\omega }}$, 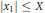 $\left| {{x}_{1}} \right|\,\le \,X$ and
$\left| {{x}_{1}} \right|\,\le \,X$ and 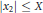 $\left| {{x}_{2}} \right|\,\le \,X$ admit a solution in integers
$\left| {{x}_{2}} \right|\,\le \,X$ admit a solution in integers 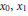 ${{x}_{0}},\,{{x}_{1}}$ and
${{x}_{0}},\,{{x}_{1}}$ and  ${{x}_{2}}$ not all zero. Answering a question of Y. Bugeaud and M. Laurent, we show that the exponents
${{x}_{2}}$ not all zero. Answering a question of Y. Bugeaud and M. Laurent, we show that the exponents 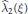 $\widehat{{{\lambda }_{2}}}\left( \xi \right)$ where
$\widehat{{{\lambda }_{2}}}\left( \xi \right)$ where 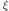 $\xi$ ranges through all real numbers with
$\xi$ ranges through all real numbers with 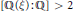 $[\mathbb{Q}(\xi )\,:\mathbb{Q}]\,>\,2$ form a dense subset of the interval
$[\mathbb{Q}(\xi )\,:\mathbb{Q}]\,>\,2$ form a dense subset of the interval 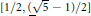 $\left[ 1/2,\,\left( \sqrt{5}\,-\,1 \right)/2 \right]$ while, for the same values of
$\left[ 1/2,\,\left( \sqrt{5}\,-\,1 \right)/2 \right]$ while, for the same values of 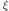 $\xi$, the dual exponents
$\xi$, the dual exponents 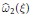 $\widehat{{{\omega }_{2}}}\left( \xi \right)$ form a dense subset of
$\widehat{{{\omega }_{2}}}\left( \xi \right)$ form a dense subset of 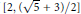 $\left[ 2,\,\left( \sqrt{5}\,+\,3 \right)/2 \right]$. Part of the proof rests on a result of V. Jarník showing that
$\left[ 2,\,\left( \sqrt{5}\,+\,3 \right)/2 \right]$. Part of the proof rests on a result of V. Jarník showing that 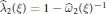 $\widehat{{{\lambda }_{2}}}\left( \xi \right)=1-{{\hat{\omega }}_{2}}{{\left( \xi \right)}^{-1}}$ for any real number
$\widehat{{{\lambda }_{2}}}\left( \xi \right)=1-{{\hat{\omega }}_{2}}{{\left( \xi \right)}^{-1}}$ for any real number 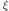 $\xi$ with
$\xi$ with 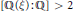 $[\mathbb{Q}(\xi )\,:\mathbb{Q}]\,>\,2$.
$[\mathbb{Q}(\xi )\,:\mathbb{Q}]\,>\,2$.
 $\text{m}$
-Primary Ideals
$\text{m}$
-Primary Ideals