Let $F$ denote a binary form of order $d$ over the complex numbers. If $r$ is a divisor of $d$, then the Hilbert covariant ${{H}_{r,\,d}}\,\left( F \right)$ vanishes exactly when $F$ is the perfect power of an order $r$ form. In geometric terms, the coefficients of $H$ give defining equations for the image variety $X$ of an embedding ${{\text{P}}^{r}}\,\to \,{{\text{P}}^{d}}$. In this paper we describe a new construction of the Hilbert covariant and simultaneously situate it into a wider class of covariants called the Göttingen covariants, all of which vanish on $X$. We prove that the ideal generated by the coefficients of $H$ defines $X$ as a scheme. Finally, we exhibit a generalisation of the Göttingen covariants to $n$-ary forms using the classical Clebsch transfer principle.

We answer the natural question: when is a transversely holomorphic symplectic foliation induced by a generalized complex structure? The leafwise symplectic form and transverse complex structure determine an obstruction class in a certain cohomology, which vanishes if and only if our question has an affirmative answer. We first study a component of this obstruction, which gives the condition that the leafwise cohomology class of the symplectic form must be transversely pluriharmonic. As a consequence, under certain topological hypotheses, we infer that we actually have a symplectic fibre bundle over a complex base. We then show how to compute the full obstruction via a spectral sequence. We give various concrete necessary and sufficient conditions for the vanishing of the obstruction. Throughout, we give examples to test the sharpness of these conditions, including a symplectic fibre bundle over a complex base that does not come from a generalized complex structure, and a regular generalized complex structure that is very unlike a symplectic fibre bundle, i.e., for which nearby leaves are not symplectomorphic.

Given a Bratteli diagram $B$, we study the set ${{\mathcal{O}}_{B}}$ of all possible orderings on $B$ and its subset ${{\mathcal{P}}_{B}}$ consisting of perfect orderings that produce Bratteli–Vershik topological dynamical systems (Vershik maps). We give necessary and sufficient conditions for the ordering $\omega $ to be perfect. On the other hand, a wide class of non-simple Bratteli diagrams that do not admit Vershik maps is explicitly described. In the case of finite rank Bratteli diagrams, we show that the existence of perfect orderings with a prescribed number of extreme paths constrains significantly the values of the entries of the incidence matrices and the structure of the diagram $B$. Our proofs are based on the new notions of skeletons and associated graphs, defined and studied in the paper. For a Bratteli diagram $B$ of rank $k$, we endow the set ${{\mathcal{O}}_{B}}$ with product measure $\mu $ and prove that there is some $1\,\le \,j\,\le \,k$ such that $\mu $-almost all orderings on $B$ have $j$ maximal and $j$ minimal paths. If $j$ is strictly greater than the number of minimal components that $B$ has, then $\mu $-almost all orderings are imperfect.

For a Lie group 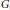$G$, we show that the map 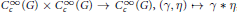$C_{c}^{\infty }\,\left( G \right)\,\times \,C_{c}^{\infty }\,\left( G \right)\,\to \,C_{c}^{\infty }\,\left( G \right),\,\left( \gamma ,\,\eta \right)\mapsto \,\gamma \,*\,\eta $ taking a pair of test functions to their convolution, is continuous if and only if 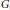$G$ is 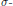$\sigma -$compact. More generally, consider 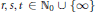$r,\,s,\,t\,\in {{\mathbb{N}}_{0}}\,\cup \,\left\{ \infty \right\}$ with 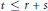$t\,\le \,r\,+\,s$, locally convex spaces 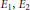${{E}_{1}}\,,\,{{E}_{2}}$ and a continuous bilinear map 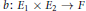$b:\,{{E}_{1}}\,\times \,{{E}_{2}}\,\to \,F$ to a complete locally convex space $F$. Let 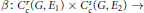$\beta :\,C_{c}^{r}\,\left( G,\,{{E}_{1}} \right)\,\times \,C_{c}^{S}\,\left( G,\,{{E}_{2}} \right)\,\to$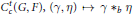$C_{c}^{t}\,\left( G,\,F \right),\,\left( \gamma ,\,\eta \right)\,\mapsto \,\gamma \,*\,b\,\eta$ be the associated convolution map. The main result is a characterization of those $\left( G,\,r,s,t,b \right)$ for which 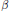$\beta$ is continuous. Convolution of compactly supported continuous functions on a locally compact group is also discussed as well as convolution of compactly supported ${{L}^{1}}$-functions and convolution of compactly supported Radon measures.

This paper concerns the problem of existence of taut foliations among 3-manifolds. From the work of David Gabai we know that a closed 3-manifold with non-trivial second homology group admits a taut foliation. The essential part of this paper focuses on Seifert fibered homology 3-spheres. The result is quite different if they are integral or rational but non-integral homology 3-spheres. Concerning integral homology 3-spheres, we can see that all but the 3-sphere and the Poincaré 3-sphere admit a taut foliation. Concerning non-integral homology 3-spheres, we prove there are infinitely many that admit a taut foliation, and infinitely many without a taut foliation. Moreover, we show that the geometries do not determine the existence of taut foliations on non-integral Seifert fibered homology 3-spheres.

The main result of this paper is a characterization of the abelian varieties $B/K$ defined over Galois number fields with the property that the $L$-function $L\left( B/K;\,s \right)$ is a product of $L$-functions of non-$\text{CM}$ newforms over $Q$ for congruence subgroups of the form ${{\Gamma }_{1}}\,\left( N \right)$. The characterization involves the structure of End$\left( B \right)$, isogenies between the Galois conjugates of $B$, and a Galois cohomology class attached to $B/K$.

We call the varieties having this property strongly modular. The last section is devoted to the study of a family of abelian surfaces with quaternionic multiplication. As an illustration of the ways in which the general results of the paper can be applied, we prove the strong modularity of some particular abelian surfaces belonging to that family, and we show how to find nontrivial examples of strongly modular varieties by twisting.

This article establishes a sufficient condition for Kobayashi hyperbolicity of unbounded domains in terms of curvature. Specifically, when $\Omega \,\subset \,{{\mathbb{C}}^{n}}$ corresponds to a sub-level set of a smooth, real-valued function Ψ such that the form $\omega \,=\,\mathbf{i}\partial \bar{\partial }\Psi $ is Kähler and has bounded curvature outside a bounded subset, then this domain admits a hermitian metric of strictly negative holomorphic sectional curvature.

“Co-Frobenius” coalgebras were introduced as dualizations of Frobenius algebras. We previously showed that they admit left-right symmetric characterizations analogous to those of Frobenius algebras. We consider the more general quasi-co-Frobenius $\left( \text{QcF} \right)$ coalgebras. The first main result in this paper is that these also admit symmetric characterizations: a coalgebra is $\text{QcF}$ if it is weakly isomorphic to its (left, or right) rational dual $\text{Rat}\left( {{C}^{*}} \right)$ in the sense that certain coproduct or product powers of these objects are isomorphic. Fundamental results of Hopf algebras, such as the equivalent characterizations of Hopf algebras with nonzero integrals as left (or right) co-Frobenius, $\text{QcF}$, semiperfect or with nonzero rational dual, as well as the uniqueness of integrals and a short proof of the bijectivity of the antipode for such Hopf algebras all follow as a consequence of these results. This gives a purely representation theoretic approach to many of the basic fundamental results in the theory of Hopf algebras. Furthermore, we introduce a general concept of Frobenius algebra, which makes sense for infinite dimensional and for topological algebras, and specializes to the classical notion in the finite case. This will be a topological algebra $A$ that is isomorphic to its complete topological dual ${{A}^{\vee }}$. We show that $A$ is a (quasi)Frobenius algebra if and only if $A$ is the dual ${{C}^{*}}$ of a (quasi)co-Frobenius coalgebra $C$. We give many examples of co-Frobenius coalgebras and Hopf algebras connected to category theory, homological algebra and the newer $q$-homological algebra, topology or graph theory, showing the importance of the concept.