Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T06:30:50.330Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuity of Convolution of Test Functions on Lie Groups

Published online by Cambridge University Press:  20 November 2018

Lidia Birth  and
Helge Glöckner
Lidia Birth
Affiliation:
Universität Paderborn, Institut für Mathematik, Warburger Str.100, 33098 Paderborn, Germany e-mail: [email protected] [email protected]
Helge Glöckner
Affiliation:
Universität Paderborn, Institut für Mathematik, Warburger Str.100, 33098 Paderborn, Germany e-mail: [email protected] [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a Lie group 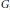$G$, we show that the map 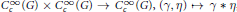$C_{c}^{\infty }\,\left( G \right)\,\times \,C_{c}^{\infty }\,\left( G \right)\,\to \,C_{c}^{\infty }\,\left( G \right),\,\left( \gamma ,\,\eta \right)\mapsto \,\gamma \,*\,\eta $ taking a pair of test functions to their convolution, is continuous if and only if 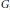$G$ is 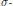$\sigma -$compact. More generally, consider 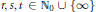$r,\,s,\,t\,\in {{\mathbb{N}}_{0}}\,\cup \,\left\{ \infty \right\}$ with 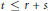$t\,\le \,r\,+\,s$, locally convex spaces 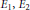${{E}_{1}}\,,\,{{E}_{2}}$ and a continuous bilinear map 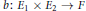$b:\,{{E}_{1}}\,\times \,{{E}_{2}}\,\to \,F$ to a complete locally convex space $F$. Let 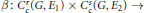$\beta :\,C_{c}^{r}\,\left( G,\,{{E}_{1}} \right)\,\times \,C_{c}^{S}\,\left( G,\,{{E}_{2}} \right)\,\to$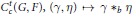$C_{c}^{t}\,\left( G,\,F \right),\,\left( \gamma ,\,\eta \right)\,\mapsto \,\gamma \,*\,b\,\eta$ be the associated convolution map. The main result is a characterization of those 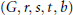$\left( G,\,r,s,t,b \right)$ for which 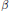$\beta$ is continuous. Convolution of compactly supported continuous functions on a locally compact group is also discussed as well as convolution of compactly supported 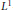${{L}^{1}}$-functions and convolution of compactly supported Radon measures.

Keywords

22E3046F0522D1542A8543A1043A1546A0346A1346E25Lie grouplocally compact groupsmooth functioncompact supporttest functionsecond countabilitycountable basissigma-compactnessconvolutioncontinuityseminormproduct estimates
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 1 , February 2014 , pp. 102 - 140
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Ardanza-Trevijano, S. and Chasco, M. J., The Pontryagin duality of sequential limits of topological Abelian groups. J. Pure Appl. Algebra 202(2005), no. 1–3, 11–21. http://dx.doi.org/10.1016/j.jpaa.2005.02.006 Google Scholar
[2] Außenhofer, L., Contributions to the duality theory of abelian topological groups and to the theory of nuclear groups. Dissertationes Math. 384(1999).Google Scholar
[3] Außenhofer, L., On the nuclearity of dual groups. arxiv:1209.3993. July 2007.Google Scholar
[4] Außenhofer, L., On the Hausdorff variety generated by all locally kω groups and on Schwartz groups. Topol. Appl. 159(2012), no. 9, 2248–2257. http://dx.doi.org/10.1016/j.topol.2011.11.058 Google Scholar
[5] Bargetz, C., Convolution of distribution-valued functions. Applications. Rev. Colombiana Mat. 45(2011), no. 1, 51–80.Google Scholar
[6] Bargetz, C., Topological tensor products and the convolution of vector-valued distributions. Doctoral Dissertation, University of Innsbruck, 2012.Google Scholar
[7] Bauer, H., Maβ-und Integrationstheorie. Second ed., de Gruyter, Berlin, 1992.Google Scholar
[8] Berg, C., Christensen, J. P. R., and Ressel, P., Harmonic analysis on semigroups. Graduate Texts in Mathematics, 100, Springer-Verlag, New York, 1984.Google Scholar
[9] Biller, H., Analyticity and naturality of the multi-variable functional calculus. Expo. Math. 25(2007), no. 2, 131–163. http://dx.doi.org/10.1016/j.exmath.2006.09.001 Google Scholar
[10] Birth, L., Untersuchungen zur Faltung auf Liegruppen. Diplomarbeit (advised by H. Glöckner), University of Paderborn, 2011.Google Scholar
[11] Bisgaard, T. M., The topology of finitely open sets is not a vector space topology. Arch. Math. 60(1993), no. 6, 546–552. http://dx.doi.org/10.1007/BF01236081 Google Scholar
[12] Bourbaki, N., Topological vector spaces. Chapters 1–5, Elements of Mathematics, Springer-Verlag, Berlin, 1987.Google Scholar
[13] Bourbaki, N., General topology. Chapters 1–4, Elements of Mathematics (Berlin), Springer-Verlag, Berlin, 1989.Google Scholar
[14] Ehrenpreis, L., Analytic functions and the Fourier transform of distributions. I. Ann. of Math. 63(1956), 129–159. http://dx.doi.org/10.2307/1969993 Google Scholar
[15] Engelking, R., General topology. Sigma Series in Pure Mathematics, 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[16] Folland, G. B., A course in abstract harmonic analysis. Studies in Advanced Mathematics. CRC Press, Boca Raton, FL, 1995.Google Scholar
[17] Gimperlein, H., Krötz, B., and Lienau, C., Analytic factorization of Lie group representations. J. Funct. Anal. 262(2012), no. 2, 667–681. http://dx.doi.org/10.1016/j.jfa.2011.10.002 Google Scholar
[18] Glöckner, H., Lie groups without completeness restrictions, Banach Center Publ. 55(2002), 43–59.Google Scholar
[19] Glöckner, H., Lie group structures on quotient groups and universal complexifications for infinite-dimensional Lie groups. J. Funct. Anal. 194(2002), 347–409. http://dx.doi.org/10.1006/jfan.2002.3942 Google Scholar
[20] Glöckner, H., Lie groups over non-discrete topological fields. arxiv:math/0408008. Google Scholar
[21] Glöckner, H., Applications of hypocontinuous bilinear maps in infinite-dimensional differential calculus. In: Generalized Lie theory in mathematics, physics and beyond, Springer, Berlin, 2009, pp. 171–186.Google Scholar
[22] Glöckner, H., Continuity of bilinear maps on direct sums of topological vector spaces. J. Funct. Anal. 262(2012), no. 5, 2013–2030. http://dx.doi.org/10.1016/j.jfa.2011.12.018 Google Scholar
[23] Glöckner, H., Upper bounds for continuous seminorms and special properties of bilinear maps. Topology Appl. 159(2012), no. 13, 2990–3001. http://dx.doi.org/10.1016/j.topol.2012.05.010 Google Scholar
[24] Glöckner, H., Continuity of LF-algebra representations associated to representations of Lie groups. Kyoto J. Math., to appear. arxiv:1203.3418v3. Google Scholar
[25] Glöckner, H., Gramlich, R., and Hartnick, T., Final group topologies, Kac-Moody groups and Pontryagin duality. Israel J. Math. 177(2010), 49–101. http://dx.doi.org/10.1007/s11856-010-0038-5 Google Scholar
[26] Glöckner, H., Lucht, L. G., and Porubský, Š., General Dirichlet series, arithmetic convolution equations and Laplace transforms. Stud. Math. 193(2009), no. 2, 109–129. http://dx.doi.org/10.4064/sm193-2-2 Google Scholar
[27] Hamilton, R. S., The inverse function theorem of Nash and Moser. Bull. Amer. Math. Soc. 7(1982), no. 1, 65–222. http://dx.doi.org/10.1090/S0273-0979-1982-15004-2 Google Scholar
[28] Herv´e, M., Analyticity in infinite-dimensional spaces. de Gruyter Studies in Mathematics, 10,Walter de Gruyter & Co., Berlin, 1989.Google Scholar
[29] Hirai, T., Shimomura, H., Tatsuuma, N., and Hirai, E., Inductive limits of topologies, their direct product, and problems related to algebraic structures. J. Math. Kyoto Univ. 41(2001), no. 3, 475–505.Google Scholar
[30] Jarchow, H., Locally convex spaces. Mathematical Textbooks, B. G. Teubner, Stuttgart, 1981.Google Scholar
[31] Lang, S., Fundamentals of differential geometry. Graduate Texts in Mathematics, 191, Springer-Verlag, 1999.Google Scholar
[32] Larcher, J.,Multiplications and convolutions in L. Schwartz’ spaces of test functions and distributions and their continuity. arxiv:1209.4174. Google Scholar
[33] Michor, P.W., Manifolds of differentiable mappings. Shiva Mathematics Series, 3, Shiva Publishing, Nantwich, 1980.Google Scholar
[34] Milnor, J., Remarks on infinite-dimensional Lie groups. In: Relativité, groupes et topologie II (Les Houches, 1983), North-Holland, Amsterdam, 1984, pp. 1007–1057.Google Scholar
[35] Neeb, K.-H. and Olafsson, G., Reflection positivity and conformal symmetry. arxiv:1206.2039v1. Google Scholar
[36] Rudin, W., Functional analysis. McGraw-Hill Series in Higher Mathematics, McGraw-Hill, New York, 1973.Google Scholar
[37] Rudin, W., Real and complex analysis. Third ed., McGraw-Hill, New York, 1987.Google Scholar
[38] Schaefer, H. H. and Wolff, M. P., Topological vector spaces. Graduate Texts in Mathematics, 3, Springer-Verlag, New York, 1999.Google Scholar
[39] Schwartz, L., Théorie des distributions. Publications de l'Institut de Math´ematique de l'Université de Strasbourg, No. IX–X, Hermann, Paris, 1966.Google Scholar
[40] Shiraishi, R., On θ-convolutions of vector-valued distributions. J. Sci. Hiroshima Univ. Ser. A-I Math. 27(1963), 173–212.Google Scholar
[41] Voigt, J., On the convex compactness property for the strong operator topology. Note Mat. 12(1992), 259–269.Google Scholar