Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T04:59:55.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Frobenius Algebras and Hopf Algebras

Published online by Cambridge University Press:  20 November 2018

Miodrag Cristian Iovanov
Miodrag Cristian Iovanov*
Affiliation:
University of Southern California, Department of Mathematics, 3620 South Vermont Ave. KAP 108, Los Angeles, California 90089-2532/ e-mail: [email protected] [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

“Co-Frobenius” coalgebras were introduced as dualizations of Frobenius algebras. We previously showed that they admit left-right symmetric characterizations analogous to those of Frobenius algebras. We consider the more general quasi-co-Frobenius 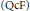$\left( \text{QcF} \right)$ coalgebras. The first main result in this paper is that these also admit symmetric characterizations: a coalgebra is 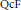$\text{QcF}$ if it is weakly isomorphic to its (left, or right) rational dual 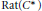$\text{Rat}\left( {{C}^{*}} \right)$ in the sense that certain coproduct or product powers of these objects are isomorphic. Fundamental results of Hopf algebras, such as the equivalent characterizations of Hopf algebras with nonzero integrals as left (or right) co-Frobenius, 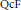$\text{QcF}$, semiperfect or with nonzero rational dual, as well as the uniqueness of integrals and a short proof of the bijectivity of the antipode for such Hopf algebras all follow as a consequence of these results. This gives a purely representation theoretic approach to many of the basic fundamental results in the theory of Hopf algebras. Furthermore, we introduce a general concept of Frobenius algebra, which makes sense for infinite dimensional and for topological algebras, and specializes to the classical notion in the finite case. This will be a topological algebra $A$ that is isomorphic to its complete topological dual 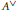${{A}^{\vee }}$. We show that $A$ is a (quasi)Frobenius algebra if and only if $A$ is the dual 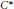${{C}^{*}}$ of a (quasi)co-Frobenius coalgebra $C$. We give many examples of co-Frobenius coalgebras and Hopf algebras connected to category theory, homological algebra and the newer $q$-homological algebra, topology or graph theory, showing the importance of the concept.

Keywords

16T1518G3516T0520N9918D1005E10coalgebraHopf algebraintegralFrobeniusQcFco-Frobenius.
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 1 , February 2014 , pp. 205 - 240
Copyright
Copyright © Canadian Mathematical Society 2014

References

[A] Abe, E., Hopf Algebras. Cambridge University Press, Cambridge, 1977.Google Scholar
[Ab] Abrams, L., Two-dimensional topological quantum field theories and Frobenius algebras. J. Knot Theory Ramifications 5(1996), 569–587. http://dx.doi.org/10.1142/S0218216596000333 Google Scholar
[AF] Anderson, D. and Fuller, K., Rings and Categories of Modules. Graduate Texts in Math. Vol. 13, Springer, Berlin–Heidelberg–New York, 1974.Google Scholar
[B] Bichon, J., N-Complexes et algebres de Hopf. C. R. Acad. Sci. Paris Ser. I 337(2003), 441–444. http://dx.doi.org/10.1016/j.crma.2003.09.002 Google Scholar
[CKQ] Chin, W., Kleiner, M., and Quinn, D., Almost split sequences for comodules. J. Algebra 249(2002), 1–19. http://dx.doi.org/10.1006/jabr.2001.9086 Google Scholar
[CM] Chin, W. and Montgomery, S., Basic coalgebras. AMS/IP Stud. Adv. Math. 4(1997), 41–47.Google Scholar
[CNO] Cuadra, J., Năstăsescu, C., and Van Oystaeyen, F., Graded almost noetherian rings and applications to coalgebras. J. Algebra 256(2002), 97–110. http://dx.doi.org/10.1016/S0021-8693(02)00099-6 Google Scholar
[CT04] Cuadra, J. and Torrecillas, B., Serial coalgebras. J. Pure Appl. Algebra 189(2004), 89–107. http://dx.doi.org/10.1016/j.jpaa.2003.11.005 Google Scholar
[DIN] Dăscălescu, S., Iovanov, M. C., and Năstăsescu, C., Path subcoalgebras, finiteness properties, and quantum groups. J. Noncommut. Geom., to appear.Google Scholar
[D] Doi, Y., Homological Coalgebra. J. Math. Soc. Japan 33(1981), 31–50.http://dx.doi.org/10.2969/jmsj/03310031 Google Scholar
[D-V] Dubois-Violette, M., dN = 0: generalized homology. K-Theory 14(1998), 371–404.http://dx.doi.org/10.1023/A:1007786403736 Google Scholar
[DNR] Dăscălescu, S., Năstăsescu, C., and Raianu, Ş., Hopf Algebras: an introduction. Lecture Notes in Pure Appl. Math. 235, Marcel Dekker, New York, 2001.Google Scholar
[F] Faith, C., Algebra II: Ring Theory. Grundlehren der MathematischenWissenschaften 191, Springer-Verlag, Berlin–Heidelberg–New York, 1976.Google Scholar
[G] Gabriel, P., Des catégories abéliennes. Bulletin de la S.M.F. 90(1962), 323–448.Google Scholar
[GTN] Gomez-Torrecillas, J. and Năstăsescu, C., Quasi-co-Frobenius coalgebras. J. Algebra 174(1995), 909–923. http://dx.doi.org/10.1006/jabr.1995.1158 Google Scholar
[GMN] Gomez-Torrecillas, J., Manu, C., and Năstăsescu, C., Quasi-co-Frobenius coalgebras II. Comm. Algebra 31(2003), 5169–5177. http://dx.doi.org/10.1081/AGB-120023152 Google Scholar
[HR74] Heyneman, R. and Radford, D., Reflexivity and Coalgebras of Finite Type. J. Algebra 28(1974), 215–246. http://dx.doi.org/10.1016/0021-8693(74)90035-0 Google Scholar
[INV06] Castaño-Iglesias, F., Năstăsescu, C., and Vercruysse, J., Quasi-Frobenius Functors. Applications.arxiv:math/0612662. Google Scholar
[ITh] Iovanov, M. C., The Representation Theory of Profinite Algebras. In: Interactions with Category Theory, Algebraic Topology and Compact Groups, PhD Thesis, SUNY Buffalo, 2009.Google Scholar
[I] Iovanov, M. C., Co-Frobenius Coalgebras. J. Algebra 303(2006), 146–153; arxiv:math/0604251, xxx.lanl.gov/abs/math.QA/0604251. http://dx.doi.org/10.1016/j.jalgebra.2006.04.028 Google Scholar
[I09] Iovanov, M. C., When Does the Rational Torsion Split Off for Finitely Generated Modules. Algebr. Represent. Theory 12(2009), 287–309. DOI 10.1007/s10468-009-9144-7 http://dx.doi.org/10.1007/s10468-009-9144-7 Google Scholar
[IR12] Iovanov, M. C. and Raianu, S., The bijectivity of the antipode revisited. Comm. Algebra 39(2011), 4662–4668. http://dx.doi.org/10.1080/00927872.2011.617273 Google Scholar
[Kap96] Kapranov, M., On the q-analogue of Homological algebra. Preprint, arxiv:9611005v1; arxiv.org/PS cache/q-alg/pdf/9611/9611005v1.pdf. Google Scholar
[Kas] C. Kassel, , Quantum Groups. Graduate Texts in Math. 155, Springer-Verlag, 1995.Google Scholar
[KW] Kassel, C. and Wambst, M., Algebre homologique des N-complexes et homologie de Hochschild aux racines de l'unite. Publ. Res. Inst. Math. Sci. Kyoto 34(1998) 91–114. http://dx.doi.org/10.2977/prims/1195144755 Google Scholar
[L] I-Peng Lin, B., Semiperfect coalgebras. J. Algebra 49(1977), 357–373. http://dx.doi.org/10.1016/0021-8693(77)90246-0 Google Scholar
[LS] Larson, R. G. and Sweedler, M. E., An associative orthogonal bilinear form for Hopf algebras. Amer. J. Math. 91(1969), 75–94. http://dx.doi.org/10.2307/2373270 Google Scholar
[M42a] Mayer, W., A new homology theory. I. Ann. of Math. 43(1942), 370–380. http://dx.doi.org/10.2307/1968874 Google Scholar
[M42b] Mayer, W., A new homology theory. II. Ann. of Math. 43(1942), 594–605. http://dx.doi.org/10.2307/1968874 Google Scholar
[M] Montgomery, S., Hopf algebras and their actions on rings. Amer. Math. Soc., Providence, RI, 1993.Google Scholar
[MTW] Menini, C., Torrecillas Jover, B., and Wisbauer, R.,Strongly rational comodules and semiperfect Hopf algebras over QF rings. J. Pure Appl. Algebra 155(2001), 237–255. http://dx.doi.org/10.1016/S0022-4049(99)00097-3 Google Scholar
[Par81] Pareigis, B., A noncommutative noncocommutative Hopf algebra in “nature”. J. Algebra 70(1981), 356–374. http://dx.doi.org/10.1016/0021-8693(81)90224-6 Google Scholar
[R] Radford, D. E., Finiteness conditions for a Hopf algebra with a nonzero integral. J. Algebra 46(1977), 189–195. http://dx.doi.org/10.1016/0021-8693(77)90400-8 Google Scholar
[R1] Radford, D., Coreflexive coalgebras. J. Algebra 26(1973), 512–535. http://dx.doi.org/10.1016/0021-8693(73)90012-4 Google Scholar
[Rad82] Radford, D. E., On the structure of pointed coalgebras. J. Algebra 77(1982), 1–14. http://dx.doi.org/10.1016/0021-8693(82)90274-5 Google Scholar
[Ra] Raianu, ş., An easy proof for the uniqueness of integrals. In: Hopf algebras and quantum groups (Brussels, 1998), Lecture Notes in Pure and Appl. Math. 209, Dekker, New York, 2000, 237–240.Google Scholar
[Si] Simson, D., Incidence coalgebras of intervally finite posets, their integral quadratic forms and comodule categories. Colloq. Math. 115(2009), 259–295. http://dx.doi.org/10.4064/cm115-2-9 Google Scholar
[Su] Sullivan, J. B., The uniqueness of integrals for Hopf algebras and some existence theorems of integrals for commutative Hopf algebras. J. Algebra 19(1971), 426–440. http://dx.doi.org/10.1016/0021-8693(71)90100-1 Google Scholar
[Sw] Sweedler, M. E., Hopf Algebras. Benjamin, New York, 1969.Google Scholar
[Sw1] Sweedler, M. E., Integrals for Hopf algebras. Ann. Math. 89(1969), 323–335. http://dx.doi.org/10.2307/1970672 Google Scholar
[St] ştefan, D., The uniqueness of integrals (a homological approach). Comm. Algebra 23(1995), 1657–1662. http://dx.doi.org/10.1080/00927879508825302 Google Scholar
[Tak] Takeuchi, M., Topological Coalgebras. J. Algebra 97(1985), 505–539. http://dx.doi.org/10.1016/0021-8693(85)90062-6 Google Scholar
[Tak77] Takeuchi, M., Morita theorems for categories of comodules. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 24(1977), 629–644.Google Scholar
[Taf71] Taft, E. J., The Order of the Antipode of Finite-dimensional Hopf Algebra. Proc. Nat. Acad. Sci. USA 68(1971), 2631–2633. http://dx.doi.org/10.1073/pnas.68.11.2631 Google Scholar
[vD] van Daele, A., The Haar measure on finite quantum groups. Proc. Amer. Math. Soc. 125(1997), 3489–3500. http://dx.doi.org/10.1090/S0002-9939-97-04037-9 Google Scholar
[vD1] van Daele, A., An algebraic framework for group duality. Adv. Math. 140(1998), 323–366. http://dx.doi.org/10.1006/aima.1998.1775 Google Scholar
[W] Weibel, C., An introduction to homological algebra. Cambridge Stud. Adv. Math. 38, Cambridge University Press, Cambridge, 1994.Google Scholar