1. Introduction
We all use mathematics in everyday life, whether to calculate the change given to us in the store, to tell time, or to choose the shortest line in the grocery store. Not only humans use math; numerical cognition abilities are important for survival across species: fish join the larger shoal to reduce their chances of being eaten, bees can identify flowers by counting the number of their petals, and so forth (Agrillo et al. Reference Agrillo, Petrazzini, Bisazza and Henik2016; Gross et al. Reference Gross, Pahl, Si, Zhu, Tautz and Zhang2009; Pisa & Agrillo Reference Pisa and Agrillo2008). These efforts have led to the widely accepted view that humans and animals are born with a “sense for number” – the ability to perceive, manipulate, and understand numerosities (Cantlon et al. Reference Cantlon, Platt and Brannon2009b; Dehaene Reference Dehaene1997; Feigenson et al. Reference Feigenson, Dehaene and Spelke2004) – and that this ability, along with general cognitive abilities, enables humans to understand more complex mathematical principles. Recently, however, it has been suggested that perceiving numerosities might not be as innate and automatic as previously thought. Instead, a new line of theories suggest that a “sense of magnitude” that enables discrimination between different continuous magnitudes, such as between the densities of two groups of apples or the total surface areas of two pizza trays, is even more basic and automatic than a sense of numbers (Henik et al. Reference Henik, Gliksman, Kallai and Leibovich2017; Gebuis & Reynvoet Reference Gebuis and Reynvoet2012a; Leibovich & Ansari Reference Leibovich and Ansari2016; Leibovich et al. Reference Leibovich, Henik and Salti2015; Reference Leibovich, Kallai, Itamar and Henik2016a; Mix et al. Reference Mix, Huttenlocher and Levine2002a).
In this review, we introduce the mainstream theories in the field of numerical cognition (e.g., number sense theory) and the studies on which these theories are based. Specifically, we concentrate on studies that employed comparison of non-symbolic stimuli (i.e., groups of items) and point out how the results of such studies can be explained by a sense of magnitude and not necessarily number. Later, we explain the sense of magnitude theory and review studies that directly demonstrate that continuous magnitudes are more automatic and basic than numerosities. The idea of a sense of magnitude, or a general system that processes all magnitudes, is not new (for a review, see Mix & Sandhofer [2007]). In fact, this idea was popular before the 1990s (e.g., Meck & Church Reference Meck and Church1983; Moyer & Landauer Reference Moyer and Landauer1967) and was neglected with the increased popularity of the number sense theory. The current review integrates new evidence supporting this idea. Importantly, we review empirical evidence suggesting that processing of continuous magnitudes, and not number (i.e., discrete numerosity), is innate and automatic. We also discuss the role of domain-general factors such as language and cognitive control in the acquisition of the concept of number. Lastly, we discuss possible implications of the sense of magnitude theory on research in numerical cognition and the diagnosis and amelioration of learning disabilities specific for math (i.e., developmental dyscalculia [DD]).
2. Mainstream theories in the field of numerical cognition
Because numbers play an important role in our lives, research has long been occupied with the cognitive structures underlying numerical cognition. We present three major theories that are at the forefront of the field and have set the tone for research in numerical cognition and the procedures for diagnosis of math learning difficulties (MLDs) and DD. The theories are summarized in Figure 1.

Figure 1. Main theories in numerical cognition (based on Leibovich et al. Reference Leibovich, Kallai, Itamar and Henik2016a). (A) The model suggested by Dehaene and Changeux (Reference Dehaene and Changeux1993), emphasizing the existence of an innate “numerosity detector” that sums numerosities regardless of continuous magnitudes. (B) The two core systems theory (Feigenson et al. Reference Feigenson, Dehaene and Spelke2004) separating processing of small and large numbers; the main difference is ratio-dependent performance in core system 1 and violation of this dependency in core system 2. (C) The approximate number system (ANS) theory suggesting that different magnitudes (examples in the figure) are being processed by an approximate analog representation of numbers.
In his seminal book, Dehaene (Reference Dehaene1997) suggested that humans and animals are born with a “sense of number,” the ability to perceive, understand, and manipulate numerosities. For example, when encountering six strawberries, we can sense their “sixness” similarly to the way we sense their redness (Burr & Ross Reference Burr and Ross2008; Nieder & Dehaene Reference Nieder and Dehaene2009), suggesting that perceiving numerosities is as basic as perceiving colors. Dehaene and Changeux (Reference Dehaene and Changeux1993) suggested a computational model explaining the process of numerosity estimation. According to this model, items are first represented spatially, according to their location. These locations are then mapped onto a topographic map. This map codes only locations and ignores all other features of the items, including continuous magnitude (like the size of an individual item). Finally, specialized neurons sum the numerosities from this map, allowing us to estimate the numerosity of a heterogeneous group of items. This model was later supported by further evidence in the work of Verguts and Fias (Reference Verguts and Fias2004) (see Fig. 1A).
Feigenson et al. (Reference Feigenson, Dehaene and Spelke2004) expanded on the original concept of the number sense. They proposed the existence of two distinct core systems of numerical representation in humans and animals; core system 1 represents large numerosities (>4), and core system 2 represents small numerosities (1–4) (see Fig. 1B). Both core systems are considered cross modal and cross species. Core system 1 forms abstract and approximate representations of large numerosities. This system allows numerical discrimination from infancy and recognition of ordinal relationships. This system's discrimination depends on the ratio between the quantities, regardless of continuous magnitudes; as we get older, the sensitivity of this system increases, and we can discriminate relatively similar numerosities. For example, 6-month-old infants can discriminate numerosities of ratio 1:2 (e.g., 20 from 40 items) but not 2:3, whereas adults can discriminate 7:8 (Barth et al. Reference Barth, Kanwisher and Spelke2003). This is consistent with Weber's law, which states that the difference in intensity needed to detect a difference between two stimuli (the difference between two numerosities, for example) is proportional to the intensities of the stimuli. Studies that reported that numerical ratio modulates performance even when numbers are presented as two symbolic numerosities (Moyer & Landauer Reference Moyer and Landauer1967) led Feigenson et al. to claim that the system allowing representation of non-symbolic numerosities is later used for complex mathematical thinking.
Core system 2 forms exact representations of small numerosities. Contrary to system 1, this system is sensitive to continuous magnitudes. In infants, this system is limited to processing and computation of three objects at most, and in adulthood, it reaches four objects. This ability to quickly, efficiently, and accurately identify small numerosities is called subitizing (Kaufman & Lord Reference Kaufman, Lord, Reese and Volkmann1949). Performance in this range is not ratio dependent. For example, infants can successfully discriminate between two versus three items but not between four versus six, despite the identical ratio (Feigenson & Carey Reference Feigenson and Carey2003). There is evidence for a connection between this system and mathematical abilities; Ashkenazi et al. (Reference Ashkenazi, Mark-Zigdon and Henik2013) found a deficit in subitizing abilities specific to children with DD. The existence of these two core systems might explain why some mathematical abilities are basic and intuitive, whereas others are considered difficult to acquire; estimations utilize core system 1, and exact numerical judgments in the subitizing range utilize core system 2. Neither system, however, is equipped to deal with exact calculations above the subitizing range (Feigenson et al. Reference Feigenson, Dehaene and Spelke2004). The studies described in this review focus mainly on numerosities above the subitizing range.
Unlike Feigenson et al. (Reference Feigenson, Dehaene and Spelke2004), Cantlon et al. (Reference Cantlon, Platt and Brannon2009b) do not distinguish between the representation of small and large numerosities. Instead, they suggest that different magnitudes, both numerical and continuous, share common representation mechanisms (see Fig. 1C), specifically that numerosities, as well as other magnitudes, are represented by an approximate number system (ANS) (for a similar view, see Cohen Kadosh & Walsh Reference Cohen Kadosh and Walsh2008; Cohen Kadosh et al. Reference Cohen Kadosh, Lammertyn and Izard2008). The first evidence supporting shared representation is that perception of different continuums, like numerosity, space, and loudness of pitch, follows Weber's law. In addition, several studies indicate that other than for numbers, the parietal lobe, and specifically the intraparietal sulcus (IPS), is activated on estimations of continuous magnitudes. Cantlon et al. (Reference Cantlon, Platt and Brannon2009b, p. 89) propose that “a system that once computed one magnitude (e.g., size) could have been hijacked to perform judgments along a new dimension (e.g., number)” (see also Henik et al. Reference Henik, Leibovich, Naparstek, Diesendruck and Rubinsten2012). It is not yet clear whether neurons in the parietal lobe are general magnitude neurons that are activated in all magnitude judgments, or whether there are specialized neurons for different magnitudes and they are all intermixed in the same area (for further discussion, see Leibovich & Ansari Reference Leibovich and Ansari2016).
The theories mentioned previously emphasize the existence of a built-in module that can “sense” numerosities. There are, however, some theoretical concerns regarding these theories. Mix et al. (Reference Mix, Huttenlocher and Levine2002a) claim that the evidence showing that infants can process numerosities is ambiguous. When comparing two sets of stimuli of different numerosities, in addition to numerosity there are differences in overall contour length, total surface area, and so forth. These continuous magnitudes can serve as an alternative explanation to a number sense. Previous studies have referred to these confounds and tried to break the correlation between numerosity and continuous magnitudes. However, a re-examination of the literature indicates that the influence of continuous magnitudes on performance in numerosity comparison tasks cannot be ruled out (Gebuis & Reynvoet Reference Gebuis and Reynvoet2012a; Reference Gebuis and Reynvoet2012b; Gebuis et al. Reference Gebuis, Gevers and Cohen Kadosh2014; Hurewitz et al. Reference Hurewitz, Gelman and Schnitzer2006; Leibovich & Ansari Reference Leibovich and Ansari2016; Leibovich & Henik Reference Leibovich and Henik2013; Soltész & Szücs Reference Soltész and Szücs2014). We now review the evidence supporting the number sense view and discuss its validity in the light of theoretical and methodological considerations.
3. Re-examination of behavioral evidence for the number sense
Non-symbolic stimuli are useful when studying basic numerosity processing; they can be used with different populations – adults, infants, and animals. Non-symbolic stimuli, however, also contain non-numerical continuous magnitudes. Because of the potential influence of these continuous magnitudes and because it is impossible to create two sets of items that differ in numerosity only (Leibovich & Henik Reference Leibovich and Henik2013; see also Fig. 2), various studies have employed different methods to try to minimize the effect of continuous magnitudes in numerosity comparison tasks. Three main methods are used to do so. The first method is to manipulate one of the continuous magnitudes (i.e., keep one continuous magnitude constant across different numerosities) or to manipulate one continuous magnitude so it is not correlated with numerosity. The second method is to manipulate different continuous magnitudes in each trial so that in a given stimulus, only one magnitude is manipulated, but throughout the experiment, several magnitudes are manipulated. The third method uses different congruency conditions between numerosity and continuous magnitudes. We now demonstrate the different methods and show why it is still possible that continuous magnitudes affect participant performance.
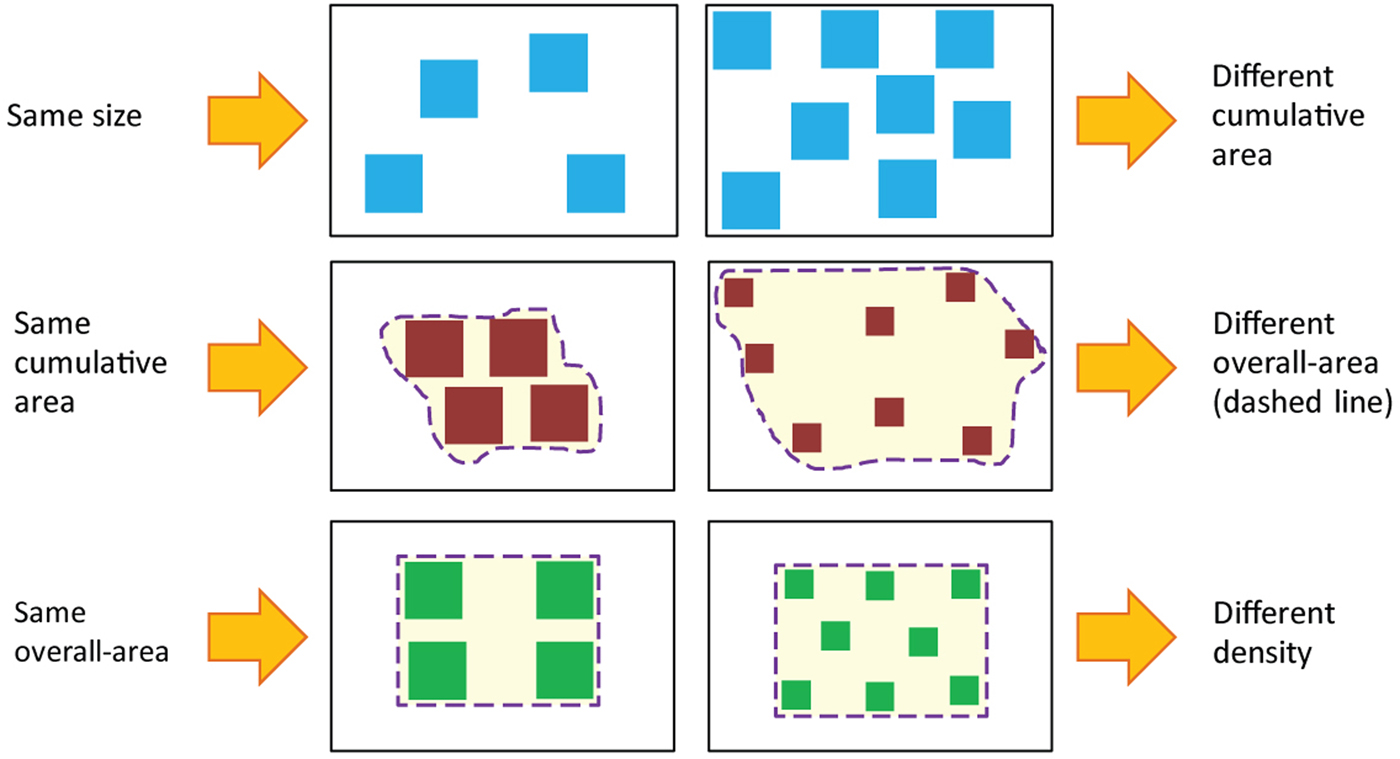
Figure 2. Correlation between number and continuous magnitudes. As illustrated in the figure, an attempt to equate one continuous magnitude in two different groups of items changes other continuous magnitudes, so that it is virtually impossible to get two groups of items that will vary only in their numerosity. Reprinted from Leibovich and Henik (Reference Leibovich and Henik2013).
The first method is based on the logic that continuous magnitudes are correlated with each other; therefore, it is sufficient to manipulate only one continuous magnitude. For example, as the average size of a set of stimuli increases, the total circumference of the dots, the total area they occupy, and so forth also increase. In the study of Abreu-Mendoza and Arias-Trejo (Reference Abreu-Mendoza and Arias-Trejo2015), participants were presented with two arrays of items and were asked to decide which array had more items. To prevent participants from using continuous magnitudes in making their decision, the total surface areas of the arrays were equal. It is impossible, however, to change one continuous magnitude (total area in this case) without changing the others. In this example, when equating the areas of two arrays with different numerosities, the less numerous array has a greater average diameter necessarily. Hence, participants can rely on average diameter when making a decision. Accordingly, in this study, even though it is reasonable to assume that the numerical decision was not based on area, it is still possible it was made using other continuous magnitudes and not necessarily numerosity (for more studies that used a similar method, see Chassy & Grodd Reference Chassy and Grodd2012; Im et al. Reference Im, Zhong and Halberda2016; Mussolin et al. Reference Mussolin, Mejias and Noël2010).
In the second method, several continuous magnitudes are manipulated throughout the experiment, but in a given stimulus, only one magnitude is manipulated. For example, Halberda et al. (Reference Halberda, Mazzocco and Feigenson2008) asked 14-year-olds to decide which of two colored dots were more numerous in a single array of yellow and blue dots. In half of the trials, the average size of the blue dots was equal to the average size of yellow dots. In the other half, the total areas of blue and yellow dots were identical. As in the first method, in a given trial, participants can use the other continuous magnitudes that were not manipulated. For example, in trials in which the areas of the dots were equal, the more numerous dots were smaller. These other continuous magnitudes can be used as a predictor of numerosity. Empirical data demonstrate this weakness; Tokita and Ishiguchi (Reference Tokita and Ishiguchi2010) asked adult participants to compare target numerosity with standard (5, 10, 20, or 40) numerosity. In a third of the trials, the areas of individual dots were equated; in another third, the total area of the arrays were equated; and in the remaining third, both were equated. The Weber fraction and the point of subjective equality (PSE; i.e., the point at which the perceived numerosities of target and standard stimuli seem equal) were calculated for all conditions. Participants underestimated numerosity of large elements and overestimated numerosity of small elements. Namely, continuous magnitudes affected performance even when they were manipulated differently in different trials (for more studies that use this method, see Barth et al. Reference Barth, La Mont, Lipton and Spelke2005; Eger et al. Reference Eger, Pinel, Dehaene and Kleinschmidt2015; Fazio et al. Reference Fazio, Bailey, Thompson and Siegler2014; Gomez et al. Reference Gomez, Piazza, Jobert, Dehaene-Lambertz, Dehaene and Huron2015; Mussolin et al. Reference Mussolin, Mejias and Noël2010).
The third method for manipulating continuous magnitudes is to employ different congruency conditions between numerosity and continuous magnitudes. For example, in the study of Nys and Content (Reference Nys and Content2012), adult participants performed a numerical or area comparison task. The stimuli were composed of dot arrays and different congruency conditions: congruent, meaning that the more numerous array had more area than the less numerous array; and incongruent, meaning that the less numerous array had more area. An interaction was found between task and congruency. Namely, the difference in performance between congruent and incongruent trials (i.e., congruency effect) was greater in the area comparison task than in the number comparison task. In other words, number interfered more when it was irrelevant, compared with area. Accordingly, it was concluded that numerosity is a more salient cue than continuous magnitudes (for other studies using congruency, see Barth et al. Reference Barth, La Mont, Lipton and Spelke2005; Bonny & Lourenco Reference Bonny and Lourenco2013; Nys & Content Reference Nys and Content2012). There are, however, contradictory findings in the literature (Durgin Reference Durgin2008; Gebuis & Reynvoet Reference Gebuis and Reynvoet2012b; Leibovich et al. Reference Leibovich, Henik and Salti2015; Reference Leibovich, Kallai, Itamar and Henik2016a; Szücs et al. Reference Szücs, Nobes, Devine, Gabriel and Gebuis2013). Hurewitz et al. (Reference Hurewitz, Gelman and Schnitzer2006) conducted a similar study and found that numbers affected performance in the area comparison task only when the numerical ratio was closer to zero (i.e., very large differences in numerosity). They reached the opposite conclusion from Nys and Content and argued that area is a more salient cue than numerosity. Recently, Leibovich et al. (Reference Leibovich, Henik and Salti2015; Reference Leibovich, Kallai, Itamar and Henik2016a) found that number interfered with performance in a non-symbolic comparison task only if it was prompted by being the relevant dimension in a previous task.
A very strong line of evidence supporting the ANS, and especially the claim that number sense is innate, comes from cross-modal matching tasks with infants and animals. In such tasks, subjects are exposed to visual and auditory displays of a number of objects or events (see Fig. 3D); for example, a visual display of two and three dots and the sound of three tones. It has been found that subjects prefer to look at the visual display that matches the number of tones, that is, two objects when hearing two tones and three objects when hearing three tones (e.g., Jordan & Baker Reference Jordan and Baker2011; Jordan et al. Reference Jordan, Suanda and Brannon2008b). Such evidence, however, should be taken with a grain of salt. As reviewed by Cantrell and Smith (Reference Cantrell and Smith2013), with 5- to 8-month-old infants as participants, only two of six studies reported preferred matching between auditory and visual quantities (see their Table 7). In studies with newborns as participants (e.g., Izard et al. Reference Izard, Sann, Spelke and Steri2009), because of poor visual acuity, they are unlikely to be able to see objects that are placed relatively close to one another as being separate from one another, and they lack the ability to separate between object and background or between one object and another. Therefore, it is hard to interpret the results as an indication of an innate number sense. Another possibility might be that when participants hear “more,” they prefer to look at “more” (Mix et al. Reference Mix, Levine, Newcombe and Henik2016). With that being said, pinpointing the exact conditions under which cross-modal matching is observed can be very informative to further understand magnitude processing in infancy. Similarly, cross-modal priming studies were previously taken as evidence for a generalized magnitude system and not necessarily as evidence for the existence of an approximate number system (e.g., Oppenheimer et al. Reference Oppenheimer, LeBoeuf and Brewer2008).
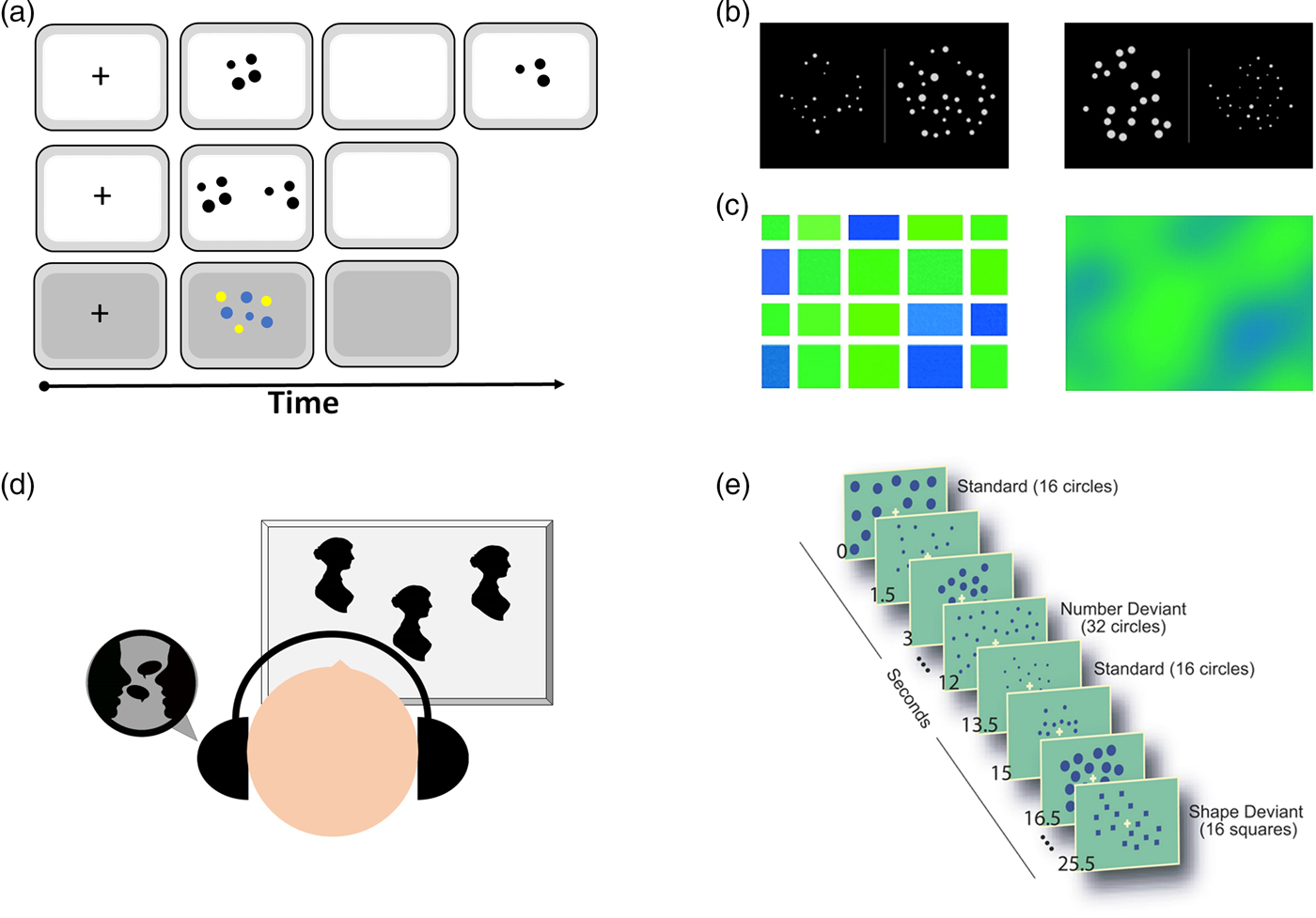
Figure 3. Examples of tasks for human participants. (A) Comparison task: two stimuli are shown side by side sequentially or simultaneously. Sometimes, one array with two colored dots is used (Agrillo et al. Reference Agrillo, Piffer, Bisazza and Butterworth2015). (B) Non-symbolic Stroop task (based on Leibovich et al. Reference Leibovich, Henik and Salti2015; Reference Leibovich, Vogel, Henik and Ansari2016b). In such a task, participants are asked to choose either the group containing more dots (e.g., number comparison task) or the group containing more area (e.g., area comparison task). All five continuous magnitudes (density, area, convex hull, etc.) are either congruent or incongruent with numerosity. (C) Castelli et al.'s (Reference Castelli, Glaser and Butterworth2006) task, in which participants need to indicate whether they see more blue or more green. The left stimulus aims to study numerosity processing, whereas the right stimulus aims to study processing of continuous magnitudes. It is clear from the left panel that the answer could be reached by both numerosity processing and continuous magnitude processing. (D) Cross-modal matching task, in which subjects are exposed to a number of visual and auditory stimuli. Looking time is longer when the numbers match than when the numbers do not match. (E) Passive habituation task (Cantlon et al. Reference Cantlon, Brannon, Carter and Pelphrey2006), in which participants are repeatedly presented with a specific numerosity. In the dishabituation phase, the number changes. To account for general detection of change, a control condition is employed in which the shape of the items, but not their number, changes.
Another line of evidence for the innate nature of the number sense comes from habituation studies with newborns and infants. In habituation studies, subjects are serially exposed to the same type of stimuli that have a common feature (e.g., the same number of items). This is done until subjects' looking time decreases. The reduction in looking time is taken as a sign that the common feature has been detected and the stimuli have lost their novelty. In the test phase, the subjects are exposed to a new stimulus (e.g., a different number of items), and the looking time is measured. When a novelty has been detected, looking time increases. To ask whether infants are born with a number sense, such habituation studies included displaying the same number of items in different spatial locations and changing the number of items in the test phase. Because the looking time of infants increased in the test phase, the conclusion was that infants are able to detect change in quantities from birth. However, as mentioned previously, changing the number of items necessarily changes continuous magnitudes. Hence, the increase in looking time can occur in response to detecting a change in different continuous magnitudes (for a detailed review, see Mix et al. Reference Mix, Huttenlocher and Levine2002a). Some works aimed to pit number against continuous magnitudes in a preferential looking time task. For example, Libertus et al. (Reference Libertus, Starr and Brannon2014) used dot arrays and changed the number of dots, keeping total surface area constant, or changed the total surface area, keeping the number constant. The authors concluded that infants preferred looking at changes in number compared with changes in total surface area. However, keeping total surface area constant does not mean that the dishabituation was to number. It could have been, for example, to the physical size of each dot, as physical size correlated with number. Because there is no way of confirming what infants habituated to, it is equally possible that these results demonstrate that “physical size of dots trumps cumulative area” (Libertus et al. Reference Libertus, Starr and Brannon2014, p. 108).
To conclude, in this section we reviewed different methods that tried to minimize the effect of continuous magnitudes in numerosity comparison tasks and habituation tasks. These methods were based on the assumption that if continuous magnitudes were not relevant and not correlated with numerosity, they would not influence performance while comparing numerosities. Some empirical studies, however, show that even under these conditions, continuous magnitudes affect numerical estimations (Cantrell et al. Reference Cantrell, Kuwabara and Smith2015b; Gebuis & Reynvoet Reference Gebuis and Reynvoet2012a). We review evidence for the role of continuous magnitude in number processing at length in section 6.
4. The origin of the number sense: Evidence from animal studies
As stated earlier, the ability to compare magnitudes is not unique to humans; it is an important ability for survival across species. Therefore, it has been argued that the number sense is not specific to humans, but is shared across species. Put differently, not only humans, but also animals are born with the ability to process numerosities (e.g., Dehaene Reference Dehaene1997; Feigenson et al. Reference Feigenson, Dehaene and Spelke2004; Nieder Reference Nieder2005).
In this context, the numerical abilities of different animals were tested – from primates to insects. Cantlon and Brannon (Reference Cantlon and Brannon2006) trained rhesus monkeys to discriminate a range of 1–9 dots per array and then tested their ability to discriminate numerosities in the range of 10–30. The authors reported that the monkeys were able to extend the numerical rule to the higher numerosity range. Moreover, response time (RT) and accuracy patterns of the monkeys were similar to those of humans in the same task; RT and error rates of both monkeys and humans increased with an increase in the similarity between the numerosities of the dots (i.e., as the numerical ratio got closer to 1). Similar findings were also reported by Beran (Reference Beran2007). In a more recent study, Viswanathan and Nieder (Reference Viswanathan and Nieder2013) searched for the underlying brain circuitry supporting numerosity representation; monkeys performed a color discrimination task of dot arrays while activity from neurons in the ventral intraparietal sulcus and the dorsolateral prefrontal cortex was recorded. The monkeys were not trained on numerosity discrimination. The authors reported neuronal activity in the tested frontal and parietal areas that was tuned to specific numerosity; different neurons showed maximal firing rates in response to different numerosities. Taken together, these studies provide evidence supporting the existence of a spontaneous number sense, enabled by frontoparietal networks in the monkey's brain.
The number sense is not restricted to the visual modality. Sometimes other senses are used to estimate magnitudes. This was demonstrated in different mammals. Meck and Church (Reference Meck and Church1983) revealed that rats can discriminate between durations and between different numerosities; rats were trained to choose between pressing on one of two levers according to a series of light flashes – one lever was associated with a longer duration, and one was associated with a shorter duration of the flashing light (see Fig. 4A). The rats were able to choose the right lever even when bursts of noise were used instead of light flashes. A more ecological example comes from the study of McComb et al. (Reference McComb, Packer and Pusey1994). This study tested the ability of lions to discriminate numerosity in the auditory modality. Specifically, McComb et al. tested whether lions (in nature) can estimate the size of an opponent group based on the number of roaring sounds. The authors used playback of one or three roars to simulate the presence of an unfamiliar intruder. According to the results, the lions were able to discriminate the number of roars and act accordingly – to take flight if the number of roars indicated the presence of more numerous lions and to stay to fight if the number of roars indicated the presence of a group with fewer lions.
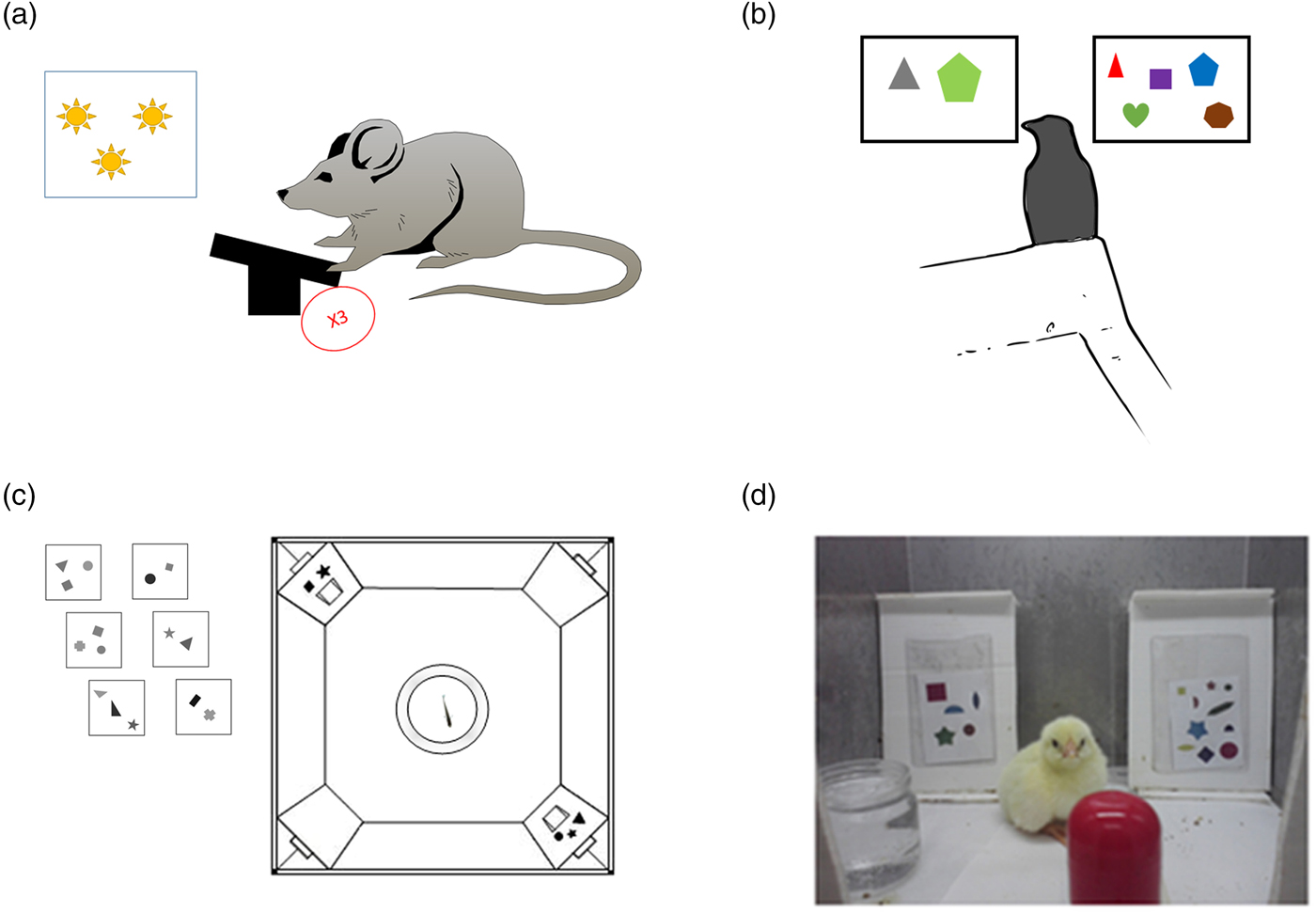
Figure 4. Examples of tasks for animals. (A) Illustration based on Meck and Church (Reference Meck and Church1983). A rat sees a number of light flashes or hears a number of tones and needs to press a lever a similar number of times to get food. (B) Birds: A jungle crow is presented with two groups of items, one containing two items and one containing five items, and is trained to peck five items. In the test phase, novel quantities are presented (Bogale et al. Reference Bogale, Kamata, Mioko and Sugita2011). (C) Fish: Fish are trained to go through the door with the larger number of items painted above it (Agrillo et al. Reference Agrillo, Dadda, Serena and Bisazza2009). (D) Chicks: Chicks are trained to select the screen with the larger number of items (Rugani et al. Reference Rugani, Vallortigara and Regolin2013).
To test how far back the number sense goes in evolution, studies were conducted with birds and fish whose brain structures differ from those of mammals and specifically primates. In these animals too, there is evidence supporting the existence of an innate number sense: Watanabe (Reference Watanabe1998) trained pigeons to respond to four objects and not respond to two objects. During the test trials, the pigeons responded to three, four, and five but not to two objects. Accordingly, the author suggested that pigeons could discriminate numerosities. Discrimination with even larger numerosities was reported in jungle crows by Bogale et al. (Reference Bogale, Kamata, Mioko and Sugita2011). In this work, jungle crows were trained to discriminate two from five. The crows also received a control test for non-numerical cues, such as spatial arrangement, shape, and total area. In the test phase, the crows showed the ability to discriminate between novel quantities, such as five and eight (see Fig. 4B). This discrimination, according to the authors, was not controlled by continuous magnitudes. Hence, the authors argued that much like other animals, jungle crows have a natural tendency to select the larger quantity and that this decision is affected by numerical ratio and stimuli magnitude. In an electrophysiological study by Ditz and Nieder (Reference Ditz and Nieder2015), crows were presented sequentially with two dot arrays and had to peck the second display of dots only if both displays contained the same numerosity. To minimize the influence of continuous magnitudes on performance, either surface area, total circumference, or the density of the dots was manipulated in different stimuli. Despite the very different neuroanatomy of birds, it was found that neurons in the endbrain of the bird (an area termed nidopallium caudolaterale [NCL]) were tuned to a preferred numerosity. Fish, too, were shown to rely on numerosity to survive: Larger groups of fish (i.e., shoals) have less chance of being attacked by predators. For this reason, a fish that successfully chooses to join a larger shoal increases its chances of survival. This was demonstrated in a study by Agrillo et al. (Reference Agrillo, Dadda, Serena and Bisazza2008). In this study, a single fish (mosquitofish) was placed in a central fish tank. This fish tank was flanked with two other fish tanks with different numbers of fish inside. It was found that the single fish spent more time next to the fish tank containing the larger number of fish. A later study by the same group (Agrillo et al. Reference Agrillo, Dadda, Serena and Bisazza2009) demonstrated that mosquitofish are able to discriminate between two and three objects even “when denied access to non-numerical information” (p. 1). In this study, fish were trained to discriminate between two and three sets of geometrical objects that varied in shape, size, brightness, and viewing distance. During the test phase, the fish were tested while controlling for one continuous magnitude at a time (see Fig. 4C). The authors reported that fish were able to discriminate two from three and that total luminance and the sum of the perimeters of the stimuli did not affect performance.
In all of these studies, however, as with humans, it was still impossible to control all of the continuous magnitudes and support claim that magnitude comparisons are based solely on numerosity judgments. For example, Cantlon and Brannon (Reference Cantlon and Brannon2006) had three different types of dot arrays. In a third of the stimuli, the densities of the two dot arrays were equal. This means that the convex hull (the area occupied by all of the dots and the area surrounding them) was larger in the array with the larger numerosity. In another third, the surface areas of the two dot arrays were equal. This means that the more numerous dots were smaller. In the remaining third of the dot arrays, the convex hulls of the two dot arrays were equal. This means that the more numerous dot array was denser. A similar approach was taken by Ditz and Nieder (Reference Ditz and Nieder2015). In some studies, only one or two continuous magnitudes were manipulated. For example, Bogale et al. (Reference Bogale, Kamata, Mioko and Sugita2011) controlled for total surface area but did not report other magnitudes such as density and convex hull. Similarly, Agrillo et al. (Reference Agrillo, Dadda, Serena and Bisazza2009) reported controlling for item size and brightness, but not other continuous magnitudes that might have influenced performance.
The inability to keep all dimensions apart from numerosity constant is true for various modalities. In the study of Meck and Church (Reference Meck and Church1983), increasing the number of flashing light events during 2 seconds meant that the tempo would be faster than when fewer flashing light events occurred in the same duration. In the study of McComb et al. (Reference McComb, Packer and Pusey1994), increasing the number of roars affected the loudness of the roars.
As in the case for studies employing non-symbolic stimuli with humans at different stages of development, the most common method to rule out the influence of continuous magnitudes is to manipulate one continuous magnitude in a given stimulus so that overall, throughout the experiment, none of the continuous magnitudes can be used as a reliable cue of numerosity. The assumption is that under these conditions, participants will not use continuous magnitudes but will base their decision only on numerosity. As we will see, however, a growing body of evidence suggests that this assumption is wrong. In fact, participants are able to use continuous magnitudes even when they are irrelevant to the task and are not a reliable cue of numerosity (Gebuis & Reynvoet Reference Gebuis and Reynvoet2012a; Reference Gebuis and Reynvoet2013; Leibovich et al. Reference Leibovich, Henik and Salti2015; Reference Leibovich, Vogel, Henik and Ansari2016b).
5. Neural correlates of non-symbolic numerosities
The number sense theory assumes the existence of a “number detector,” or specific brain tissue in the parietal lobe that is dedicated to the processing of numerosity (Piazza et al. Reference Piazza, Facoetti, Trussardi, Berteletti, Conte, Lucangeli, Dehaene and Zorzi2010). Neuroimaging studies seeking such brain tissue have used stimuli similar to those used in behavioral studies (e.g., arrays of items). This poses a problem because different ways of manipulating continuous magnitudes might result in the activity of different brain regions (or different levels of activity of the same brain regions). Studies attempting to find brain areas dedicated to the processing of numerosity have used either comparison tasks (e.g., see Fig. 3A) or passive-viewing (habituation) tasks (Fig. 3E). We now review some examples of such studies and demonstrate the difficulty in attributing activity found for such tasks to pure non-symbolic numerosity processing.
In a functional magnetic resonance imaging (fMRI) study, participants compared either the numerosities of two presented dot arrays (i.e., number comparison task) or the physical sizes of two presented disks (i.e., size comparison task; Chassy & Grodd Reference Chassy and Grodd2012). The right IPS was activated in both tasks. The contrast between the tasks revealed that the right superior parietal lobule (SPL) was more active in the number comparison than in the size comparison task, which according to the authors indicates that the SPL is involved in comparison of exact quantities. Importantly, all of the dots in the number comparison task were presented in the same size. Thus, the total area was perfectly correlated with numerosity. Hence, it is possible that instead of comparing numerosity processing with size processing, the study compared continuous magnitude processing, which requires summation of the area of all of the dots (i.e., total dot area), with size processing, which does not require such summation (i.e., comparison of disk areas), and the areas found when contrasting activity in area and dot comparison tasks might reflect this difference rather than a difference in numerosity.
In the study of Cantlon et al. (Reference Cantlon, Libertus, Pinel, Dehaene, Brannon and Pelphrey2009a), 6- to 7-year-old children and adults performed a non-symbolic numerosity comparison task. Some of the continuous magnitudes were manipulated to prevent participants from using them as indicators of numerosity. The manipulation included presenting large numerosities with small dot size and small numerosities with large dot size, while keeping the same density for all trials. The left SPL was active in both children and adults. Although the brain activity in the study was attributed to numerosity processing, another way to interpret these results is by considering the consistent correlation between dot size and numerosity. By making the more numerous dots consistently smaller than the less numerous dots, participants could theoretically have responded according to the size of the dots and not their numerosity. In addition, keeping density constant creates a correlation between numerosity and convex hull. Namely, convex hull increases with numerosity and therefore could have been used as an indicator of numerosity.
In the study of Holloway et al. (Reference Holloway, Price and Ansari2010), a different continuous magnitude manipulation was applied; adult participants were presented with two arrays of squares and were asked to choose the display side containing more squares. In these arrays, the individual size of each square varied. To prevent participants from relying on density and total surface area, these continuous magnitudes were manipulated so that in 25% of the trials, both magnitudes were congruent with numerosity (i.e., the more numerous squares were also denser, and their overall area was greater than the other array); in 25% of trials, both density and total surface area were incongruent with numerosity; and in the other 50% of trials, only density (25%) or total surface area (25%) was congruent with numerosity. Brain activity in this task was contrasted with a control condition in which the same stimuli were combined into a single irregular shape and participants were asked to decide which shape more resembled a diagonal line. The right inferior parietal lobule (IPL) and right SPL were found to be more active in the numerosity task compared with the control task. These areas are probably involved in numerosity comparison, but is that the only explanation? In addition to its role in numerical cognition, the IPL is also involved in cognitive control; IPL activity increases with conflict (Brass et al. Reference Brass, Ullsperger, Knoesche, von Cramon and Phillips2005; Greene et al. Reference Greene, Nystrom, Engell, Darley and Cohen2004). Accordingly, activity of this area can also reflect different levels of conflict in the two tasks.
Harvey et al. (Reference Harvey, Klein, Petridou and Dumoulin2013) manipulated continuous magnitudes by including several control conditions. In each condition, a different continuous magnitude was held constant. For example, density was held constant while numerosity changed (i.e., a small number of dots were presented using a large dot size, and a large number of dots were presented using a small dot size to create the same density level for different numerosities). The task included a display of a dot array that could appear in either black or white (in different trials). Adult participants were asked to indicate the color of the dots in the array. It was found that as numerosity increased, brain activity shifted from medial to lateral areas of the posterior SPL. The interpretation given by Harvey et al. indicates that the topographic organization evidence was in line with previous reports of the role of the SPL in numerosity manipulations (Cantlon et al. Reference Cantlon, Libertus, Pinel, Dehaene, Brannon and Pelphrey2009a). However, Gebuis et al. (Reference Gebuis, Gevers and Cohen Kadosh2014) claimed that it is arguable whether the neural processing was directed at pure numerosity without the confounding continuous magnitudes. Gebuis et al. pointed out that the topographic representation found in each condition actually encoded the changes in the continuous magnitudes that were not held constant in each condition. The positive relationship between numerosity and continuous magnitudes, taken together with the parietal lobe involvement in sensory integration (Calton & Taube Reference Calton and Taube2009; Naghavi & Nyberg Reference Naghavi and Nyberg2005; Shafritz et al. Reference Shafritz, Gore and Marois2002; Vallentin & Nieder Reference Vallentin and Nieder2010; Walsh Reference Walsh2003), led Gebuis et al. to propose that the suggested topographic map “reflects a weighted response of neurons that encode different sensory cues rather than a pure numerosity estimate” (p. 1).
Castelli et al.'s (Reference Castelli, Glaser and Butterworth2006) study is the only study, to the best of our knowledge, to directly compare brain areas that were active during numerosity and continuous magnitude comparison tasks. In the continuous condition, the stimulus was a rectangle containing alternating shades of green and blue. In the numerosity condition, the rectangle was composed of individual (and therefore countable) squares of blue and green rectangles. In both tasks, participants had to choose whether they were presented with “more blue or more green” (see Fig. 3C). The authors reported that bilateral regions of the IPS and regions of the parietal–occipital transition zone were significantly more active during the processing of numerosities than durig the processing of continuous magnitudes. Therefore, the results of this study were taken as evidence that the IPS is more strongly activated when numerical magnitudes are processed than when continuous magnitudes are processed. Note, however, that although in the continuous task participants were able to judge whether they saw more blue or more green only by using continuous magnitudes (e.g., area), in the numerosity task, participants were also able to base their decisions on comparison of the area covered with blue to the area covered with green. Hence, brain regions found in this contrast are not necessarily specific to numerosities.
5.1. Habituation studies at the brain level
Another way of revealing areas that are specific to numerosity processing is by using habituation studies. The idea behind such studies is to repeatedly present the same numerosity (i.e., habituation) and change all other magnitudes to find areas that will be more active when a new numerosity is eventually presented (i.e., during dishabituation). Such brain areas are assumed to be involved with the processing of numerosity. Cantlon et al. (Reference Cantlon, Brannon, Carter and Pelphrey2006) hypothesized that non-symbolic numerosity would activate the IPS in both 4-year-old children and adults. In this study, participants were repeatedly presented with 16 dots that differed in density, cumulative area, and spatial arrangement. Then, a novel stimulus was presented. In the novel stimulus, either the number of dots changed (to 32) or the shape of the dots changed (to triangles or squares; see Fig. 3E). The IPS response to novel stimuli that differed in number versus the response to novel stimuli that differed in shape was measured. Results indicated that both 4-year-old children and adults activated the IPS (bilaterally) in response to a change in number and not shape; therefore, the authors claimed that the IPS is specific to numerosity processing. This study has two limitations. The first one concerns the manipulation of only three continuous magnitudes. In a habituation study, it is important to prevent habituation effects to irrelevant properties by presenting a variety of exemplars. This principle was applied to only three continuous magnitudes, leaving all other possible magnitudes exposed to habituation. If there is at least one continuous magnitude that correlated with numerosity and was not varied consistently (total circumference, for example), the habituation is no longer specific to numerosity. The second limitation concerns the contrast between the changes in number versus the changes in shape during dishabituation. The stimuli changed by a ratio of 2:1 and from dots to squares or rectangles. In a habituation design (without an active task to reflect saliency), it is impossible to be sure that changing the number of dots from 16 to 32 has the same saliency as changing a circle to a square. Therefore, the differences in IPS activation might reflect differences in saliency.
As far as we know, there is currently only one fMRI study that was able to show a distance-dependent dishabituation of a specific brain region to a change in non-symbolic numerosity. Piazza et al. (Reference Piazza, Izard, Pinel, Le Bihan and Dehaene2004) habituated participants to a specific numerosity. The numerosities used for dishabituation varied in numerical distance from the habituated numerosity. The results revealed that the activity in the IPS region (and surrounding areas) during dishabituation correlated with the numerical distance; activity was higher for large numerical distance and smaller for small numerical distance. Accordingly, the authors suggested that numerosities are extracted automatically from a visual scene. Gebuis and Reynvoet (Reference Gebuis and Reynvoet2012a), however, argued that it is possible that participants in the study of Piazza et al. integrated multiple continuous magnitudes presented to them, because not all of the continuous magnitudes were discorrelated with numerosity.
So far we have reviewed empirical evidence supporting the claim that numerosity processing is basic, innate, and automatic (i.e., supporting the number sense theory). Specifically, we have reviewed behavioral and neuroimaging studies with animals, infants, children, and adults, concluding that numerosity processing is evolutionarily ancient, innate, and automatic; this processing takes place in dedicated brain circuitries. All of these studies share the assumption that if a continuous magnitude is not correlated with numerosity, it will not be processed and will not affect performance. Unfortunately, as mentioned before, it is impossible to avoid a correlation between numerosity and all of the continuous magnitudes at once, nor it is possible to present different numerosities with the same continuous magnitudes. Therefore, it is very possible that in the studies discussed previously, performance was affected, at least partially, by continuous magnitudes. In the next section, we review studies that directly tested the role of continuous magnitudes in numerosity comparison tasks and suggested that when making numerical comparisons, we use both numerosity and continuous magnitudes.
6. Evidence supporting holistic processing of numerosity and continuous magnitudes
To evaluate the contribution of continuous magnitudes to numerosity comparisons, adult participants compared dot arrays containing 5–25 dots each (Leibovich & Henik Reference Leibovich and Henik2014). In these dot arrays, all continuous magnitudes were manipulated at once, to be minimally correlated with numerosity, so they could not be used as a reliable cue for numerosity (Gebuis & Reynvoet Reference Gebuis and Reynvoet2011). The numerical ratio between the compared arrays and the ratio between five different continuous magnitudes were used as predictors of accuracy and RT. For both of these measures, the ratio between different continuous magnitudes explained about half of the explained variance. Namely, continuous magnitudes affected performance even though they were neither relevant to the task nor predictive of numerosity. This point has been recently demonstrated even in the subitizing range. A work by Salti et al. (Reference Salti, Katzin, Katzin, Leibovich and Henik2017) revealed that different manipulations of continuous magnitudes influence performance in a non-symbolic Stroop-like task with numerosities in the subitizing range (e.g., 2–4; for an example of a non-symbolic Stroop-like stimuli, see Fig. 3B).
Recent studies also suggested that numerosity processing might not be as automatic as previously assumed. Gebuis and Reynvoet (Reference Gebuis and Reynvoet2013) employed a habituation paradigm in which participants were adapted to specific numerosities or to specific continuous magnitudes, while event-related potentials (ERPs) were recorded. The results were analyzed twice; one analysis considered the change in numerosity to be the dishabituation event. This analysis did not reveal any brain area that detected the change. In the second analysis, however, the change in continuous magnitudes was considered to be the dishabituation event. This analysis revealed brain areas that responded to the change in continuous magnitudes. The same pattern of results was repeated even when participants were told that the numerosity of the dots would change. In the light of these results, the authors suggested that it is continuous magnitudes, and not numerosities, that are being extracted automatically from arrays of items. Similarly, in another ERP study (Soltész & Szücs Reference Soltész and Szücs2014), participants were habituated to either shape or number. Although shape adaptation occurred fast and in the range of early visual components, adaptation to number occurred only later. This pattern goes against the claim that numerosity processing is automatic like the processing of shapes and colors (Burr & Ross Reference Burr and Ross2008). Recently, DeWind and colleagues (DeWind et al. Reference DeWind, Adams, Platt and Brannon2015; Park et al. Reference Park, DeWind, Woldorff and Brannon2016b) used a new method for creating non-symbolic stimuli (groups of dots) and analyzing the influence of numerosity and of continuous magnitudes. They suggested that numerosity is processed automatically and very early in the visual stream. However, there are both methodological and empirical caveats concerning the method of DeWind and colleagues. First, in these works, it is not clear whether there is a correlation between number and continuous magnitudes, and if there is, how strong it is. This is important because a strong correlation between number and continuous magnitudes can change strategy. Namely, if, for example, the correlation between area and numerosity is 0.7, then participants can reliably choose the larger area. The findings of DeWind and colleagues can also be accounted for by the signal clarity view, stating that numbers can be more salient in habituation studies simply because they have less variance than continuous magnitudes. For example, Park et al. (Reference Park, DeWind, Woldorff and Brannon2016b) used five numerosities in their experiment. The variance in the continuous magnitudes was greater. This facilitates use of numerosity rather than other continuous magnitudes.
Recent studies also found that numerosity is not processed independently of continuous magnitudes, as proposed by the number sense theory. Gebuis and Reynvoet (Reference Gebuis and Reynvoet2014) asked participants to passively view ordinal arrays of dots (e.g., groups of three, four, five, six, and nine dots) while ERPs were recorded. A trial was composed of five dot arrays, presented consecutively. Numerosity and five continuous magnitudes (convex hull, aggregate surface, density, diameter, and contour length) always increased with numerosity in the first four-dot arrays. Namely, more dots were denser, occupied more surface area, and so forth than fewer dots (i.e., congruent). In the fifth and last dot array, the continuous magnitudes were congruent in half of the trials or incongruent with numerosity in the other half. The authors found congruity-related changes in ERPs above left parietal and mid–right frontal electrodes. Specifically, these channels showed greater positive amplitude in response to incongruent trials than to congruent trials. This result cannot be reconciled with numerosity processing that is independent of continuous magnitudes.
Although, as demonstrated previously, it is very difficult (if not impossible) to isolate brain areas that are specific to processing of numerosity independent of continuous magnitudes, there is a strong line of evidence showing a great overlap between the processing of numerosity and continuous magnitudes (Cappelletti et al. Reference Cappelletti, Gessaroli, Hithersay, Mitolo, Didino, Kanai, Cohen Kadosh and Walsh2013; Dormal et al. Reference Dormal, Andres and Pesenti2012). For example, in the fMRI study of Pinel et al. (Reference Pinel, Piazza, Le Bihan and Dehaene2004), it was found that numerical size, physical size, and luminance activated bilateral IPS and occipitotemporal regions during comparison tasks. Behavioral analysis of the results revealed that both physical size and luminance affected performance in the numerical judgment task even when they were irrelevant. The authors argued that these results demonstrate distributed processing along the IPS, with some areas specific for one magnitude and a considerable overlap between all of them. Such evidence supports the shared representation of space, time, and number suggested previously by Walsh (Reference Walsh2003).
The majority of non-symbolic comparison studies, including all imaging studies mentioned so far, examine numerosity above the subitizing range. One fMRI study that dealt specifically with performance in the subitizing range was conducted by Leibovich et al. (Reference Leibovich, Henik and Salti2015). The study manipulated the congruity of numerosity and continuous magnitudes of dot arrays (half of the trials in each task were congruent, and half were incongruent) and task order (half of the participants started with the numerosity discrimination task, and half with the area discrimination task). The results indicated that performance was faster and more accurate in the area task. Importantly, although area always affected performance in the numerosity task, numerosity affected performance in the area task only for participants who started with the numerosity discrimination task. Interestingly, the order in which the tasks were administered affected activations at the brain level. Namely, during congruent trials, the group that started with the numerosity task showed activation in the right frontoparietal areas, whereas the group that started with the area task showed activation in homologue left frontoparietal areas. This study demonstrates that even in the subitizing range, continuous magnitudes still influence performance at both behavioral and functional levels, and this effect is further modulated by task context.
Further evidence supporting shared representation of different magnitudes derives from neural recording studies in primates. In the study of Tudusciuc and Nieder (Reference Tudusciuc and Nieder2007), rhesus monkeys were presented with a sample stimulus (either a group of dots in the numerosity task or a line in the continuous task). After a short delay, a test stimulus appeared. The test stimulus matched the sample stimulus (in either numerosity or length) only in half of the trials. The monkeys had to respond only when the test stimulus matched the sample stimulus (i.e., a delayed match-to-sample task). During training, electrodes recorded the neuronal activity in the depth of the monkeys' IPS. This study revealed the existence of a neural population that was active for both the continuous and numerosity tasks, suggesting that some neural populations are involved in general magnitude processing. The authors speculated that this neuron population resides in an area equivalent to that found in humans by Pinel et al. (Reference Pinel, Piazza, Le Bihan and Dehaene2004).
In addition to studies at the brain level presented previously, molecular studies with animals provide evidence for molecular mechanisms allowing size discrimination during early visual processing. In their seminal paper, Lettvin et al. (Reference Lettvin, Maturana, McCulloch and Pitts1959) noticed that a frog's choice of food is driven by size and motion. In their own words, “He [a frog] can be fooled easily not only by a bit of dangled meat but by any moving small object” (p. 1940). This observation implies a mechanism that can discriminate between small and large objects to choose the appropriate behavior. Such size-based decisions are important for other species too. Zebrafish, for example, behave differently in response to small and large objects; the zebrafish approaches small stimuli (having the size of its prey) and avoids larger stimuli (having the size of its predators). This pattern of results was replicated even when the stimuli were not animals, but small and large squares, further supporting the suggestion of Lettvin et al. that size alone is sufficient to modify behavior. Preuss et al. (Reference Preuss, Trivedi, vom Berg-Maurer, Ryu and Bollmann2014) went further and asked which molecular mechanisms can explain such behavior. These authors provided direct evidence revealing that neurons in the deeper layer of the tectum (the uppermost part of the midbrain) provide inhibitory input to the tectum in response to small objects. In contrast, the superficial neurons in this area provide inhibitory output to the tectum, unless a large object comes into view (see also Abbas & Meyer Reference Abbas and Meyer2014). These two studies suggest that the processing of size is very basic and innate. Hence, it is possible that size and other continuous magnitudes play an important role not only in evolutionarily older animals, but also in primates and particularly in humans.
7. The role of continuous magnitudes in numerical cognition
So far we have reviewed some studies that support the number sense theory and some that do not. One reason for these contradicting findings can be the result of different ways of manipulating continuous magnitudes. This possibility was tested recently by Smets et al. (Reference Smets, Sasanguie, Szücs and Reynvoet2015; but see also Gebuis & Reynvoet Reference Gebuis and Reynvoet2012c). The authors employed several conditions to directly evaluate the influence of different methods of continuous magnitude manipulation on performance in non-symbolic estimation and comparison tasks. In the first condition, the surface area was kept constant in half of the trials and diameter was kept constant in the other half; in the second condition, four continuous magnitudes (convex hull, total surface, average diameter, and density) were manipulated at once so they were not correlated with the numerical ratio; and in the third condition, all continuous magnitudes were correlated with numerosities. Performance (measured using the Weber fraction, a measure based on accuracy that describes the smallest difference in numerosity that can still be discriminated) was modulated by the method of controlling continuous magnitudes; performance was worst when manipulating four continuous magnitudes simultaneously, better when only one continuous magnitude was manipulated, and best when all of the continuous magnitudes were correlated with numerosity. The differences in performance were more noticeable when the numerosities were more similar (i.e., having higher numerical ratios). A similar pattern of results was reported by Clayton et al. (Reference Clayton, Gilmore and Inglis2015). These studies reflect one of the major problems in studying non-symbolic numerosity comparisons – performance is highly sensitive to the way researchers choose to manipulate continuous magnitudes. The question then remains, what is really measured in such tasks? Is it the ability to process numerosity? Is it the ability to integrate multiple magnitudes to make a decision? Is it the ability to inhibit irrelevant continuous magnitudes?
Such questions led to a new line of theories suggesting that continuous magnitudes play an important role in the development of basic numerical abilities. This new line of theories takes into account the natural correlation between numerosity and continuous magnitudes and proposes a general system to process different magnitudes. The logic behind these theories is that any given group of items has, in addition to numerosity, different continuous magnitudes that usually correlate with numerosity. Thus, when required to make a numerical decision, continuous magnitudes will also be used. In other words, we use all available cues to make an informed decision rather than relying on a single magnitude. Accordingly, humans (and other species) will use any information available to make decisions. In this context, Gebuis and Reynvoet (Reference Gebuis and Reynvoet2012b) suggested that developing a system unique for numbers is redundant and costly. Because numerosity and continuous magnitudes are usually positively correlated, it is more likely that we have a general magnitude system that makes numerical decisions according to both continuous magnitudes and numerosity, as suggested previously (e.g., Cantlon et al. Reference Cantlon, Platt and Brannon2009b). In other words, they propose a holistic process in which people do not extract numerosity independently from the other continuous magnitudes. Although the idea of a generalized magnitude system is not new and has been explored in multiple studies (e.g., Meck & Church Reference Meck and Church1983; Moyer & Landauer Reference Moyer and Landauer1967), these studies suggest not only that number and non-numerical magnitudes are processed by the same system, but also that the processing of non-numerical magnitudes is automatic and hence influences empirical efforts to measure the ability to compare or estimate processing of non-symbolic numerosities.
Leibovich and Henik (Reference Leibovich and Henik2013) acknowledged the challenges in assuming that numerosities are processed independently from continuous magnitudes and presented a developmental model for the acquisition of numerical knowledge. According to this model, people are not necessarily born with the ability to represent numerosities, but are able to develop this ability because of the correlation between numerosity and continuous magnitudes. Their theoretical model suggests that humans are born with the innate ability to distinguish between continuous magnitudes, not numerosities. With time, infants explore their environment and learn by experience that usually more toys will take more space in their toy box, or put more generally, that numerosity and continuous magnitudes positively correlate. It is only after understanding this correlation that the number sense and the idea of numerosity can develop (for a similar ideas see Henik et al. Reference Henik, Gliksman, Kallai and Leibovich2017).
Furthermore, a new and important theory, the signal clarity theory (Cantrell & Smith Reference Cantrell and Smith2013), suggests that the influence of numerosity on performance can be a result of the experimental design. Specifically, this view claims that an important distinction should be made between what happens in the natural environment and in an experimental setup. In the environment, numerosity and continuous magnitudes usually correlate. In an experimental setup, in contrast, researchers control and manipulate continuous magnitudes by breaking this correlation. This manipulation creates greater variance of the continuous magnitudes and very small variance in numerosity. A possible outcome is that the numerical signal is much more salient than the continuous signals. For example, if in a habituation task six items are consecutively presented and all continuous magnitudes vary, it is much more likely that participants will pay more attention to changes in numerosities. According to the signal clarity view, infants are able to learn “on-line,” during an experimental session, which dimension has the least variance and to use the information. Importantly, experiments do not use environmental scenarios; hence, the results obtained do not necessarily represent reality (Cantrell & Smith Reference Cantrell and Smith2013).
8. New outlook on the contribution of cognitive control to the development of a number sense
The theories mentioned previously and others (e.g., Gebuis & Reynvoet Reference Gebuis and Reynvoet2012b; Gevers et al. Reference Gevers, Cohen Kadosh, Gebuis and Henik2016; Henik et al. Reference Henik, Gliksman, Kallai and Leibovich2017; Leibovich & Henik Reference Leibovich and Henik2013; Mix et al. Reference Mix, Levine, Newcombe and Henik2016) suggest that numerosities and continuous magnitudes are processed holistically because they usually correlate. This correlation, however, is not perfect. An everyday example of the violation of this correlation is the following scenario in a grocery store: When waiting in line, you will usually choose to wait behind the person with the emptiest cart because usually less-filled carts carry fewer items (Fig. 5A). There are, however, exceptions to this rule; you will wait less time after a full cart containing a few large items than after a half-empty cart containing many small items (Fig. 5B).
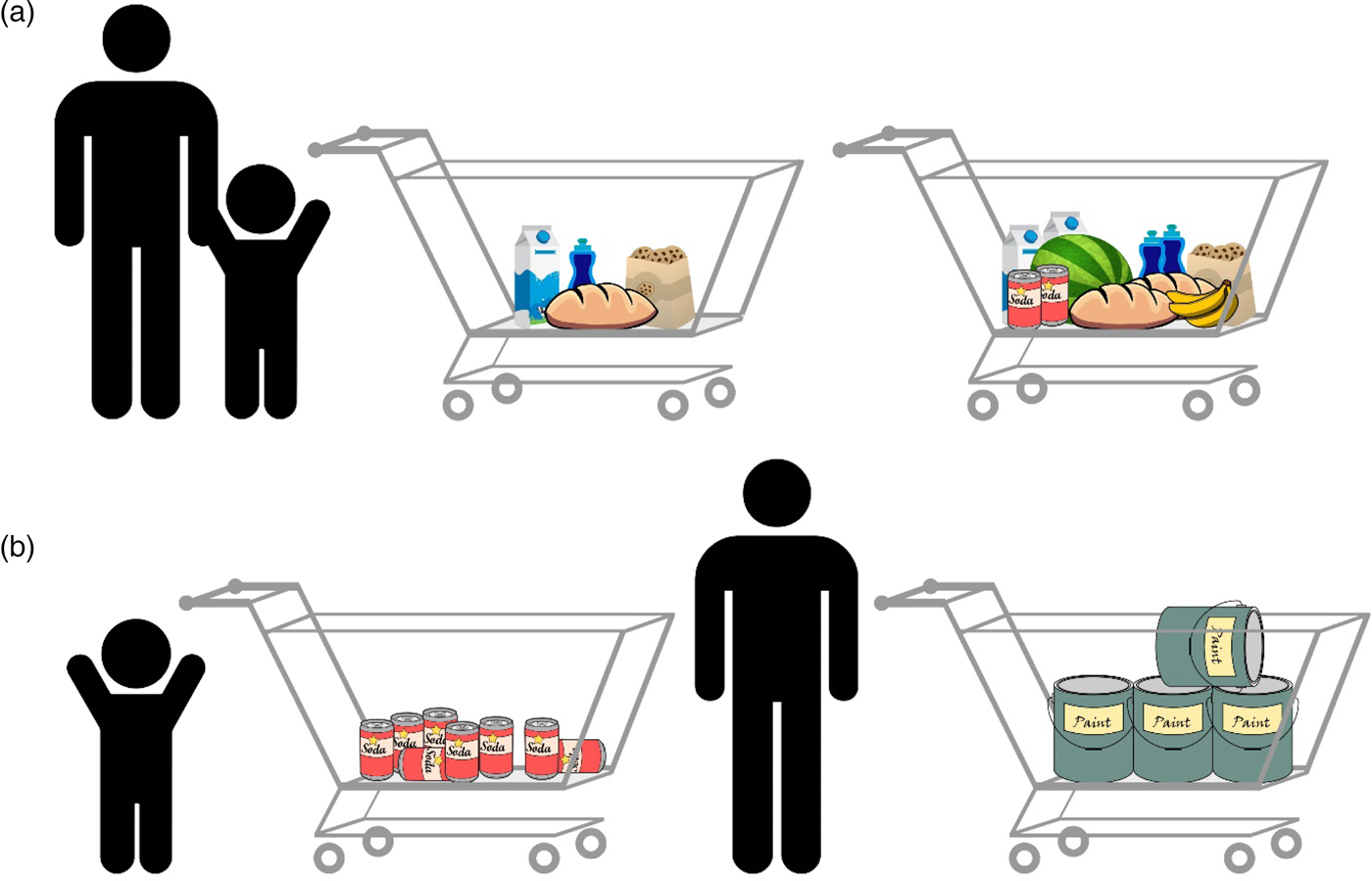
Figure 5. Numerosity comparison at the grocery store. (A) An example of a typical correlation: Usually, more items will occupy more space, will have greater surface area, and so forth in comparison with fewer items. In this case, understanding the correlation and using it facilitate performance, allowing us to make faster and more accurate decisions. Both adults and children are able to indicate which cart has more items. (B) Violation of this correlation: The full cart on the right contains fewer items, but they still take more space and have greater surface area than all of the items in the other cart. Although adults can identify the violation of the correlation and choose the fuller cart because of the ability to inhibit the influence of continuous variables, young children might not be able to understand that the full cart has fewer items.
Accordingly, it is possible that both integration and inhibition abilities, which are different aspects of cognitive control, are required to allow us to use the natural correlation between numerosities and continuous magnitudes, without being “enslaved” by it, namely, to be able to use this correlation (i.e., integration) and to deal with its violations (i.e., inhibition). It is well known that cognitive control abilities, including inhibition, develop with age (e.g., Morton Reference Morton2010). It is also known that cognitive control correlates with math abilities (e.g., Bull et al. Reference Bull, Espy and Wiebe2008). The exact role of cognitive control in the process of acquiring mathematical knowledge, however, is less clear because performance in different numerical comparison tasks does not always correlate with cognitive control abilities (Clayton & Gilmore Reference Clayton and Gilmore2015; Keller & Libertus Reference Keller and Libertus2015; Smets et al. Reference Smets, Sasanguie, Szücs and Reynvoet2015).
Additionally, in non-symbolic numerosity comparison tasks, it is virtually impossible to dissociate cognitive control from ANS acuity. The Weber fraction computed from a dot discrimination task is considered an indicator of ANS acuity. It has been demonstrated, though, that the Weber fraction is influenced by the level of congruity between numerosity and continuous magnitudes in both children and adults. Specifically, the Weber fraction was higher (i.e., performance was worse) in incongruent than in congruent trials (Tokita & Ishiguchi Reference Tokita and Ishiguchi2013). On the other hand, to avoid this confound means eliminating the conflict, that is, to use pairs of stimuli in which numerical and continuous magnitude perfectly correlate. However, in this case, one cannot be sure that participants are basing their decision on numerosity, continuous magnitude, or a combination of both. Hence, the ability to discriminate between very similar numerosities and the ability to inhibit irrelevant continuous magnitudes are inseparable. This not only is true in behavioral studies, but also might apply to neuroimaging methods; at the brain level, during incongruent trials it is reasonable to expect parietal areas to be active in response to processing numerosities, and frontal areas to be active in response to conflict. This, however, is an oversimplification because there are areas in the frontoparietal network that are involved in both cognitive control and processing of size (Brass et al. Reference Brass, Ullsperger, Knoesche, von Cramon and Phillips2005), and frontal areas that are associated with cognitive control, such as the inferior frontal gyrus (IFG), are also reported consistently in numerosity comparison tasks (Kaufmann et al. Reference Kaufmann, Koppelstaetter, Delazer, Siedentopf, Rhomberg, Golaszewski, Felber and Ischebeck2005). Another example comes from a recent fMRI study by Leibovich et al. (Reference Leibovich, Henik and Salti2015; Reference Leibovich, Vogel, Henik and Ansari2016b). In this study, participants compared the total area or the number of either congruent or incongruent dot arrays. IPS activity was found only when contrasting congruent versus incongruent trials, but not area versus dot comparison. Hence, IPS activity in this comparison task was probably related to conflict. It is possible that methods that correlate a specific pattern of activity of the same area in different tasks, such as multivariate voxel pattern analysis (MVPA), will eventually be able to partially separate ANS acuity from cognitive control, but as of now, such data do not exist.
Against this background, we put forward a theoretical model for the development of mathematical abilities. This model is similar to some recently suggested models (Mix et al. Reference Mix, Levine, Newcombe and Henik2016) in that it includes the role of continuous magnitudes and assumes a general system for processing magnitudes. This model, however, also has some unique suggestions. First, we hypothesize that number sense is not innate, but acquired. We emphasize the role of the correlation between number and continuous magnitudes in the process of learning the concept of numbers. We also take a more domain-general view and discuss the role of cognitive abilities such as individuation, language, and cognitive control in the development of the concept of number. This model expands two previously suggested models (Leibovich & Henik Reference Leibovich and Henik2013; Leibovich et al. Reference Leibovich, Kallai, Itamar and Henik2016a).
This model assumes that humans are not born with the ability to discriminate numerosities. Instead, babies use continuous magnitudes of groups of objects when comparing them. There are two reasons for this assumption. First, newborns have very poor visual acuity. Until the age of 4 weeks, babies are unable to focus their vision because muscles in the eye, fovea, and brain areas related to visual processing have not fully matured. The result is very blurry vision (Fig. 6). It is only at the age of 8 weeks that babies can focus on objects, but only at distances up to 100 cm (Banks Reference Banks1980; Dobson & Teller Reference Dobson and Teller1978). The second reason is that babies are not born with the cognitive ability to individuate objects. In other words, until the age of about 5 months, babies cannot tell where one object ends and another one begins (Carey Reference Carey2001). Without the ability to individuate, it is unclear how the concept of the number of items can even be applicable.
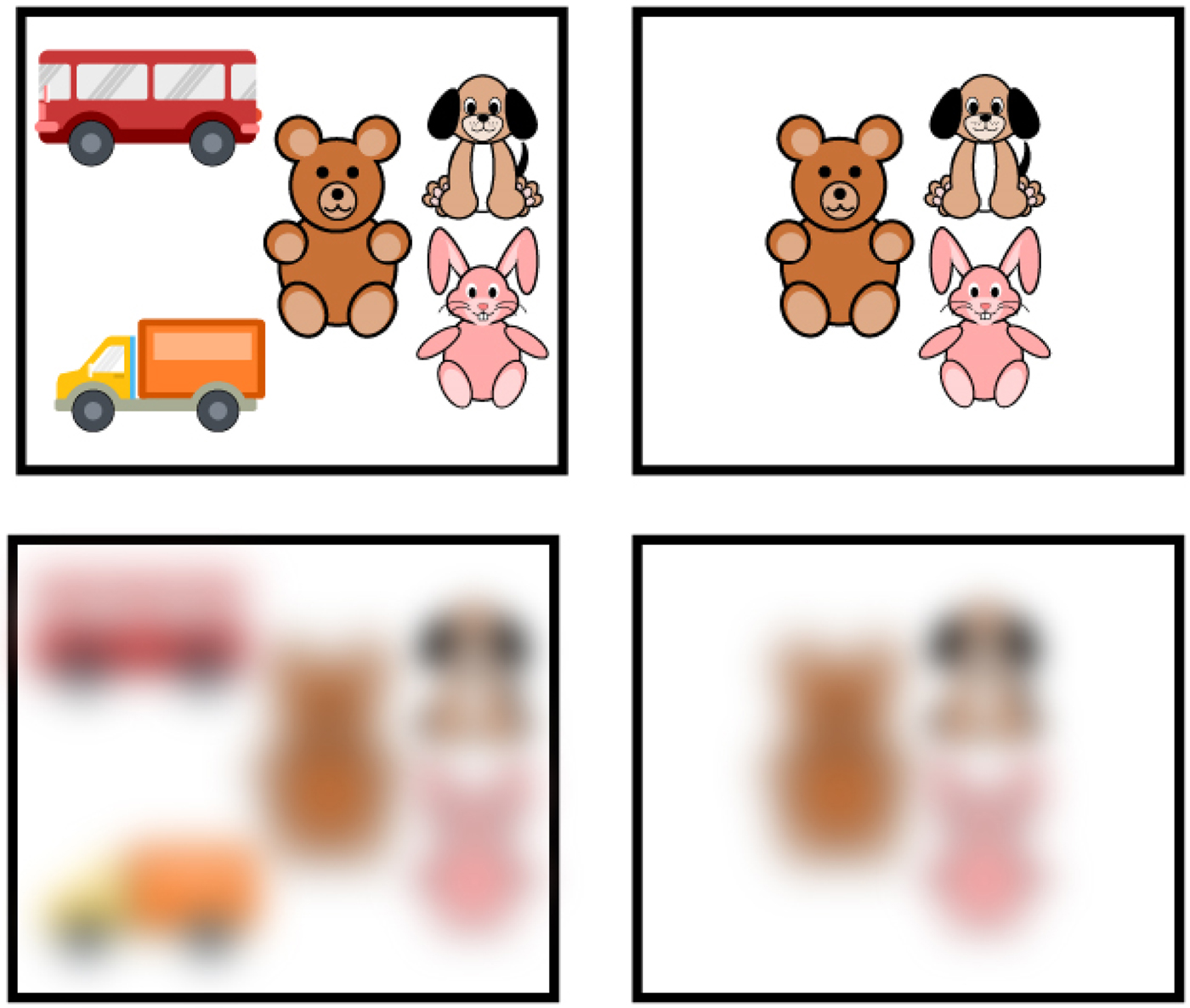
Figure 6. Poor visual acuity of newborns. Example of arrays of items and how they look with poor visual acuity. The images in the top squares demonstrate how groups of toys would look to an adult. The images in the bottom squares demonstrate how the groups of toys would look to newborns, whose visual acuity is 25 times worse than that of an adult, from a distance of more than 45 cm.
Instead of being born with a sense of numbers, we suggest that a number sense develops from understanding the correlation between numerosity and continuous magnitudes (Fig. 7). Such a process was referred to in the past as “statistical learning” (e.g., Frost et al. Reference Frost, Siegelman, Narkiss and Afek2013), in the context of object individuation: When babies notice that some properties stay together, they understand that these properties belong to the same object. Statistical learning also helps with studying language – to understand that some combinations of sounds go together more frequently (for an elaborate discussion, see Mix & Sandhofer Reference Mix, Sandhofer and Roberts2007). Therefore, it is possible that a similar process can serve in learning the natural correlation between number and continuous magnitudes. Once babies are able to individuate items, they are exposed to the natural correlation of numerosities and continuous magnitudes. For example, more candies will occupy more space on the plate. It is because of such experiences that children learn this correlation and even over-apply it by constantly integrating both numerosity and continuous magnitudes when estimating numerosities. For that critical stage to occur, first some notion of numerosity should exist. We hypothesize that it is through language, or more specifically through number words, that the discrete quantity of a set (i.e., numerosity) is emphasized. Please note that Mix et al. (Reference Mix, Levine, Newcombe and Henik2016) have recently suggested that number words orient attention toward numerosities. Over-applyication of such correlations was observed in Piaget's (Reference Piaget1952) number conservation task. In such a task, a child will see two rows containing the same number of items (e.g., coins). The items in the two rows are equally distant from one another (i.e., the two rows have the same total surface area and convex hull). The experimenter then asks the child if the two rows contain the same or different numbers of coins. The child usually answers “same.” Then, the experimenter changes the spacing of the items in one row (in front of the child), creating a larger convex hull in one row, and repeats the question. As the convex hull differences become larger, the child is more likely to indicate that the more spaced row contains more items. Older children will perform this task better; namely, they will be less confounded by the convex hull. More recently, it has been suggested that even though adults have high accuracy in such a task, they activate more cognitive control–related areas when the convex hull and the number of items are incongruent (Leroux et al. Reference Leroux, Spiess, Zago, Rossi, Lubin, Turbelin, Mazoyer, Tzourio-Mazoyer, Houdé and Joliot2009).

Figure 7. Theoretical model describing developmental landmarks of basic numerical abilities. Because of physiological constraints, newborns' vision is not acute enough to focus on specific items (Banks Reference Banks1980). Only at the age of 5 months are babies able to individuate items from the background and from one another (Carey Reference Carey2001). Individuation is critical to understanding the concept of numerosity. With the development of language and specifically number words, more attention is given to numerosities. With experience, a child learns correlations; for example, usually, more toys will take more space in the toy box. With the development of cognitive control and inhibition – general abilities that are related not only to math – a child can understand that correlations can be violated and compare numerosities even when they do not correlate with continuous variables. We suggest that this is the starting point required for basic math abilities.
To be able to deal with the violation of the correlation, proper cognitive control abilities should be developed. When inhibition abilities are well developed, it is possible to both use the correlation between numerosities and continuous magnitudes when it is appropriate and ignore continuous magnitudes when they are irrelevant, as in the case of the grocery store shopping carts mentioned earlier or when a child is asked to count the number of different-sized objects. It is only then that a child can really understand the concept of numbers and why, for example, the quantities of five apples and five watermelons are equal, even though watermelons are bigger. Count words may also play an important role in emphasizing numerosity over continuous magnitudes. As suggested by Mix et al. (Reference Mix, Levine, Newcombe and Henik2016), “Count words signal that number is a distinct property, independent of these other quantitative dimensions” (p. 20). In their work, they also review evidence suggesting that adults in Western cultures that do not have number words have problems discriminating or estimating large quantities.
9. Outstanding questions and future directions
9.1. Specifying the role of cognitive control in the development of basic numerical abilities
The role of cognitive control in the development of basic numerical abilities is not yet clear. One major challenge is that cognitive control is in fact a compilation of abilities. Hence, the first challenge is to find ways to “separate,” if possible, numerical cognition abilities from cognitive control abilities. As discussed previously, it is virtually impossible to create a non-symbolic comparison task without creating the need to use cognitive control.
A second challenge stems from the fact that there is no single measure of cognitive control, and different studies that correlate math abilities with cognitive control test different cognitive control components. For example, one possible division relates to three major components: inhibition, updating, and shifting. These components consist of several sub-components (Miyake et al. Reference Miyake, Friedman, Emerson, Witzki, Howerter and Wager2000). Let us consider the case of inhibition. Two hallmark tasks to measure inhibition are the Stroop and flanker tasks. In the Stroop task, a color word is presented in a font color that is either congruent to the word (e.g., the word RED printed in red color) or incongruent (e.g., the word RED printed in green color). In the flanker task, subjects are asked to report the direction of the middle arrow in a horizontal line consisting of five arrows. Here too, the middle arrow can be congruent with the flanking arrows (e.g., all arrows are pointing right: ![]() ) or incongruent with the flanking arrows (e.g., the middle arrow is pointing left and the flanking arrows are pointing right:
) or incongruent with the flanking arrows (e.g., the middle arrow is pointing left and the flanking arrows are pointing right: ![]() ). It has been demonstrated that performance in these two different tasks, both aimed at measuring inhibition, do not correlate (Shilling et al. Reference Shilling, Chetwynd and Rabbitt2002). To examine the role of cognitive control in the context of numerical abilities, different studies used different tasks to measure cognitive control, for example, the NEPSY (A Developmental Neuropsychological Assessment)-II inhibition subset, in which participants view a picture of a circle and need to say “square” (Gilmore et al. 2013; Keller & Libertus Reference Keller and Libertus2015); the Stroop task with words or numbers (Bull & Scerif Reference Bull and Scerif2001; St Clair-Thompson & Gathercole Reference St Clair-Thompson and Gathercole2006); delayed response (Espy et al. Reference Espy, McDiarmid, Cwik, Stalets, Hamby and Senn2004); peg tapping (Blair & Razza Reference Blair and Razza2007); and many more (for a review see Cragg & Gilmore Reference Cragg and Gilmore2014). Those different studies drew different conclusions regarding the correlation between math abilities and inhibition abilities, maybe because different tasks tap into different aspects of inhibition, and some aspects can be more related to math abilities than others.
). It has been demonstrated that performance in these two different tasks, both aimed at measuring inhibition, do not correlate (Shilling et al. Reference Shilling, Chetwynd and Rabbitt2002). To examine the role of cognitive control in the context of numerical abilities, different studies used different tasks to measure cognitive control, for example, the NEPSY (A Developmental Neuropsychological Assessment)-II inhibition subset, in which participants view a picture of a circle and need to say “square” (Gilmore et al. 2013; Keller & Libertus Reference Keller and Libertus2015); the Stroop task with words or numbers (Bull & Scerif Reference Bull and Scerif2001; St Clair-Thompson & Gathercole Reference St Clair-Thompson and Gathercole2006); delayed response (Espy et al. Reference Espy, McDiarmid, Cwik, Stalets, Hamby and Senn2004); peg tapping (Blair & Razza Reference Blair and Razza2007); and many more (for a review see Cragg & Gilmore Reference Cragg and Gilmore2014). Those different studies drew different conclusions regarding the correlation between math abilities and inhibition abilities, maybe because different tasks tap into different aspects of inhibition, and some aspects can be more related to math abilities than others.
It is important to understand the specific mechanisms of inhibition and cognitive control in general in numerical cognition. One way to shed light on this topic is to use a variety of tasks that measure cognitive control and examine their correlations with numerical abilities. Nevertheless, one should always be aware that correlation is not a causality, and direct empirical studies should be conducted to determine the underlying role of cognitive control in the development of numerical cognition.
9.2. The role of continuous magnitudes in dyscalculia
The reviewed body of work suggests that number sense may not be innate. Hence, it is important to ask how number sense develops in typically developed children and in children and adults with learning difficulties specific to mathematics (i.e., DD or MLD). DD and MLD manifest in different behaviors, which led Rubinsten and Henik (Reference Rubinsten and Henik2009) to suggest that different brain dysfunctions may underlie each syndrome. The authors proposed a distinction between “pure” DD, comorbid DD (with attention deficit hyperactivity disorder [ADHD]/dyslexia), and MLD that arises from different brain dysfunctions. With respect to “pure” DD (which is attributed to dysfunction of the IPS), one possibility that comes to mind in this context is that difficulty in understanding the correlation between numerosity and continuous magnitudes can lead to impaired number sense and poor math abilities. This suggestion can be tested empirically. For example, by using a numerosity comparison task with different levels of congruency (Gebuis & Reynvoet Reference Gebuis and Reynvoet2012b), one can empirically test the ability of individuals with dyscalculia to rely on continuous magnitudes when they correlate with numerosity. Specifically, in typically developed adults, accuracy was found to increase when the number of continuous magnitudes that positively correlated with numerosity increased, suggesting that participants were able to use the correlation between continuous magnitudes and numerosities. If performance of individuals with dyscalculia does not have a similar pattern, it might mean that individuals with dyscalculia are not aware of the correlation between numerosities and continuous magnitudes. This would be a domain-specific account of dyscalculia (see also Gliksman et al. Reference Gliksman, Naparstek, Ifergane and Henik2015).
There are, however, new studies suggesting a more domain-general account for dyscalculia. For example, in the study of Bugden and Ansari (Reference Bugden and Ansari2016), children with dyscalculia and typically developed children performed a non-symbolic comparison task in which the total area of the dots was either congruent or incongruent with numerosity. Although both groups performed similarly in the congruent trials, children with dyscalculia performed worse in the incongruent trials. Such a pattern suggests a more domain-general account of dyscalculia because the only difference between those with DD and typically developed children was in incongruent trials that required cognitive control. Such studies also demonstrate the importance of understanding the specific role of cognitive control, facilitation, and inhibition in numerical cognition, as discussed previously.
9.3. Asking the right question: A neural base for holistic processing of numerosities
As demonstrated, it is virtually impossible to separate continuous magnitudes from numerosity processing, especially without triggering other cognitive processes such as cognitive control. Because number and continuous magnitudes cannot be separated, it is virtually impossible to empirically design a study that will show that only continuous magnitudes are processed or only numerosities are processed. Accordingly, at the brain level, it becomes difficult to define brain areas dedicated to numerosity processing. We would like to argue that in the light of compelling evidence for holistic processing of numerosity and continuous magnitudes, a suitable goal would be to ask which brain areas support integration of different dimensions of magnitudes (i.e., holistic processing). It has already been suggested by Walsh (Reference Walsh2003) that space, time, and number are all being processed in the parietal lobe because integration of this information is needed to direct actions in the real world, for example, to know when to cross the road when a car is approaching. Indeed, areas in the parietal lobe, such as the IPS and the SPL, were found to be active during numerosity processing but also during tasks requiring integration of information (Graziano 2000; Jancke Reference Jancke2001). This integration might not be limited to these areas; for example, the right temporoparietal junction was found to be involved in feature integration. Specifically, right temporoparietal junction activity was found to be modulated by the number of congruent features presented to participants, even from multisensory inputs (Calvert et al. Reference Calvert, Campbell and Brammer2000; Pollmann et al. Reference Pollmann, Zinke, Baumgartner, Geringswald and Hanke2014). Pursuing a line of research that asks about integration of information throughout development and testing such integration abilities in individuals with different math abilities can broaden what we know about brain areas supporting numerical cognition and can help define which abilities should be improved to improve math abilities.
10. Conclusion
The main goal of this review is to encourage researchers not to assume that number sense is simply innate, but to put this hypothesis (almost regarded as an axiom) to the test. The theoretical model presented in this review raises more questions than answers. It is important to understand that the ANS theory and the suggested model are not mutually exclusive, and therefore, providing evidence against one theory does not necessarily mean that the other theory is right. This is especially true in the light of the methodological challenges of studying numerosity in isolation from continuous magnitudes. It is our hope that this review and our theoretical model will start a discussion that will result in new and exciting research directions aimed at investigating the possible role of continuous magnitudes and cognitive control abilities in typical and atypical development of math abilities. Such research directions can have crucial implications for the way we study behavioral and neural mechanisms relating to numerical cognition in humans and other species. Furthermore, these different directions can also lead to changes in the way basic math is taught and the way math difficulties are diagnosed and ameliorated.
ACKNOWLEDGMENTS
This work was supported by the European Research Council (ERC) under the European Union's Seventh Framework Programme (FP7/2007–2013)/ERC Grant Agreement 295644 to Avishai Henik.
The authors thank Ashael Raveh for his help with designing the figures for this article.











Target article
From “sense of number” to “sense of magnitude”: The role of continuous magnitudes in numerical cognition
Related commentaries (29)
A “sense of magnitude” requires a new alternative for learning numerical symbols
Approximate number sense theory or approximate theory of magnitude?
Commentary on Leibovich et al.: What next?
Computational foundations of the visual number sense
Controlling for continuous variables is not futile: What we can learn about number representation despite imperfect control
Direct and rapid encoding of numerosity in the visual stream
Evidence for a number sense
From continuous magnitudes to symbolic numbers: The centrality of ratio
How not to develop a sense of number
Infants discriminate number: Evidence against the prerequisite of visual object individuation and the primacy of continuous magnitude
Infants, animals, and the origins of number
Innateness of magnitude perception? Skill can be acquired and mastered at all ages
Is the ANS linked to mathematics performance?
Magnitude rather than number: More evidence needed
Magnitude, numerosity, and development of number: Implications for mathematics disabilities
Multitudes are adaptable magnitudes in the estimation of number
Number faculty is alive and kicking: On number discriminations and number neurons
Numerical intuitions in infancy: Give credit where credit is due
Numerical magnitude evaluation as a foundation for decision making
Perceiving numerosity from birth
Right idea, wrong magnitude system
Selecting the model that best fits the data
The contribution of fish studies to the “number sense” debate
The contributions of non-numeric dimensions to number encoding, representations, and decision-making factors
The evolvement of discrete representations from continuous stimulus properties: A possible overarching principle of cognition
The number sense is neither last resort nor of primary import
What is a number? The interplay between number and continuous magnitudes
What is the precise role of cognitive control in the development of a sense of number?
Why try saving the ANS? An alternative proposal
Author response
Toward an integrative approach to numerical cognition