Part XIV. Quantum Mechanics and Locality
Where the Theory of Probability Fails
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 616-623
-
- Article
- Export citation
Part XV. Language and Thought
Must Beliefs be Sentences?
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 626-643
-
- Article
- Export citation
A Reply to Brian Loar's “Must Beliefs be Sentences?”
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 644-653
-
- Article
- Export citation
Beliefs and Concepts: Comments on Brian Loar “Must Beliefs Be Sentences?”
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 654-661
-
- Article
- Export citation
Reply to Fodor and Harman
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 662-666
-
- Article
- Export citation
Part XVI. Commensurability, Comparability, Communicability
Commensurability, Comparability, Communicability
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 668-688
-
- Article
- Export citation
Implications of Incommensurability
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 689-703
-
- Article
- Export citation
Comment on Kuhn's “Commensurability, Comparability, Communicability”
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 704-711
-
- Article
- Export citation
Response to Commentaries
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 712-716
-
- Article
- Export citation
Part XVII. The Sure-Thing Principle
The Sure Thing Principle
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 718-730
-
- Article
- Export citation
Front matter
PBM volume 1982 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. fi-fx
-
- Article
-
- You have access
- Export citation


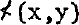 is the (small) angle between x and y so that 0 ≤
is the (small) angle between x and y so that 0 ≤