Research Article
Regularity of the solutions for elliptic problems on nonsmooth domains in ℝ3. Part II: Regularity in neighbourhoods of edges
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 517-545
-
- Article
- Export citation
Robustness and convergence of suboptimal controls in distributed parameter systems
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1153-1179
-
- Article
- Export citation
Local existence and blow-up criterion for the Boussinesq equations
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 935-946
-
- Article
- Export citation
Diffusion-mediated permanence problem for a heterogeneous Lotka–Volterra competition model
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 281-336
-
- Article
- Export citation
The second Hamiltonian structure for the periodic Toda lattice
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 547-566
-
- Article
- Export citation
Eigenvalue problems for the wave equation with strong damping
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 755-771
-
- Article
- Export citation
Cauchy problem for the Ginzburg-Landau equation for the superconductivity model
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1181-1192
-
- Article
- Export citation
Some new properties of Sobolev mappings: intersection theoretical approach
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 337-358
-
- Article
- Export citation
Positive definite temperature functions and a correspondence to positive temperature functions
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 947-961
-
- Article
- Export citation
Periodic oscillations of forced pendulums with very small length*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 67-76
-
- Article
- Export citation
Existence and uniqueness of discontinuous solutions for a hyperbolic system
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1193-1205
-
- Article
- Export citation
Invariant radicals
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 773-780
-
- Article
- Export citation
Stable summands of U(n)
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 963-973
-
- Article
- Export citation
Travelling wave solutions for a balance law
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 567-593
-
- Article
- Export citation
Regularity of the solutions for elliptic problems on nonsmooth domains in ℝ3, Part I: countably normed spaces on polyhedral domains
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 77-125
-
- Article
- Export citation
On the zeros of the second derivative
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 359-368
-
- Article
- Export citation
Global well-posedness and conservation laws for the water wave interaction equation
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 369-384
-
- Article
- Export citation
Singular boundary value problems for P-Laplacian-like equations
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 975-981
-
- Article
- Export citation
Inhomogeneous Fuchs equations and the limit cycles in a class of near-integrable quadratic systems
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1207-1217
-
- Article
- Export citation
Stability and instability of steady-state solutions for a hydrodynamic model of semiconductors
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 781-796
-
- Article
- Export citation

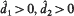 such that for every
such that for every 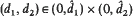 the RD-model is
the RD-model is 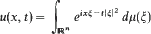
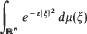
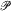 is introduced to give an isomorphism between the class ofall positive definite temperature functions and the class of all possible temperature functions in
is introduced to give an isomorphism between the class ofall positive definite temperature functions and the class of all possible temperature functions in 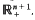 Then correspondence given by
Then correspondence given by 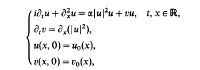
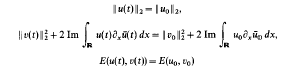
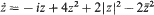 which represents one of two codimension-five components in the intersection of two strata in the centre manifold,
which represents one of two codimension-five components in the intersection of two strata in the centre manifold, 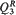 and
and