We consider a model of binary opinion dynamics where one opinion is inherently “superior” than the other, and social agents exhibit a “bias” toward the superior alternative. Specifically, it is assumed that an agent updates its choice to the superior alternative with probability α > 0 irrespective of its current opinion and opinions of other agents. With probability 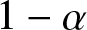$1-\alpha$, it adopts majority opinion among two randomly sampled neighbors and itself. We are interested in the time it takes for the network to converge to a consensus on the superior alternative. In a complete graph of size n, we show that irrespective of the initial configuration of the network, the average time to reach consensus scales as 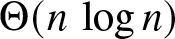$\Theta(n\,\log n)$ when the bias parameter α is sufficiently high, that is, $\alpha \gt \alpha_c$ where αc is a threshold parameter that is uniquely characterized. 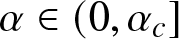When the bias is low, that is, when $\alpha \in (0,\alpha_c]$, we show that the same rate of convergence can only be achieved if the initial proportion of agents with the superior opinion is above certain threshold 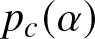$p_c(\alpha)$. If this is not the case, then we show that the network takes 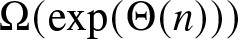$\Omega(\exp(\Theta(n)))$ time on average to reach consensus.

Motivated by Ahmadi-Javid (Journal of Optimization Theory Applications, 155(3), 2012, 1105–1123) and Ahmadi-Javid and Pichler (Mathematics and Financial Economics, 11, 2017, 527–550), the concept of Tsallis Value-at-Risk (TsVaR) based on Tsallis entropy is introduced in this paper. TsVaR corresponds to the tightest possible upper bound obtained from the Chernoff inequality for the Value-at-Risk. The main properties and analogous dual representation of TsVaR are investigated. These results partially generalize the Entropic Value-at-Risk by involving Tsallis entropies. Three spaces, called the primal, dual, and bidual Tsallis spaces, corresponding to TsVaR are fully studied. It is shown that these spaces equipped with the norm induced by TsVaR are Banach spaces. The Tsallis spaces are related to the $L^p$ spaces, as well as specific Orlicz hearts and Orlicz spaces. Finally, we derive explicit formula for the dual TsVaR norm.

A system experiences random shocks over time, with two critical levels, d1 and d2, where $d_{1} \lt d_{2}$. k consecutive shocks with magnitudes between d1 and d2 partially damaging the system, causing it to transition to a lower, partially working state. Shocks with magnitudes above d2 have a catastrophic effect, resulting in complete failure. This theoretical framework gives rise to a multi-state system characterized by an indeterminate quantity of states. When the time between successive shocks follows a phase-type distribution, a detailed analysis of the system’s dynamic reliability properties such as the lifetime of the system, the time it spends in perfect functioning, as well as the total time it spends in partially working states are discussed.

We study three classes of shock models governed by an inverse gamma mixed Poisson process (IGMP), namely a mixed Poisson process with an inverse gamma mixing distribution. In particular, we analyze (1) the extreme shock model, (2) the δ-shock model, and the (3) cumulative shock model. For the latter, we assume a constant and an exponentially distributed random threshold and consider different choices for the distribution of the amount of damage caused by a single shock. For all the treated cases, we obtain the survival function, together with the expected value and the variance of the failure time. Some properties of the inverse gamma mixed Poisson process are also disclosed.

In this paper, the ordering properties of convex and increasing convex orders of the dependent random variables are studied. Some closure properties of the convex and increasing convex orders under independent random variables are extended to the dependent random variables under the Archimedean copula. Two applications are provided to illustrate our results.

In this paper, we introduce a novel way to quantify the remaining inaccuracy of order statistics by utilizing the concept of extropy. We explore various properties and characteristics of this new measure. Additionally, we expand the notion of inaccuracy for ordered random variables to a dynamic version and demonstrate that this dynamic information measure provides a unique determination of the distribution function. Moreover, we investigate specific lifetime distributions by analyzing the residual inaccuracy of the first-order statistics. Nonparametric kernel estimation of the proposed measure is suggested. Simulation results show that the kernel estimator with bandwidth selection using the cross-validation method has the best performance. Finally, an application of the proposed measure on the model selection is provided.

Imagine, you enter a grocery store to buy food. How many people do you overlap with in this store? How much time do you overlap with each person in the store? In this paper, we answer these questions by studying the overlap times between customers in the infinite server queue. We compute in closed form the steady-state distribution of the overlap time between a pair of customers and the distribution of the number of customers that an arriving customer will overlap with. Finally, we define a residual process that counts the number of overlapping customers that overlap in the queue for at least $\delta$ time units and compute its distribution.

In this paper, we establish some stochastic comparison results for largest claim amounts of two sets of independent and also for interdependent portfolios under the setup of the proportional odds model. We also establish stochastic comparison results for aggregate claim amounts of two sets of independent portfolios. Further, stochastic comparisons for largest claim amounts from two sets of independent multiple-outlier claims have also been studied. The results we obtained apply to the whole family of extended distributions, also known as the Marshall–Olkin family of distributions. We have given many numerical examples to illustrate the results obtained.

We study site and bond percolation in simple directed random graphs with a given degree distribution. We derive the percolation threshold for the giant strongly connected component and the fraction of vertices in this component as a function of the percolation probability. The results are obtained for degree sequences in which the maximum degree may depend on the total number of nodes n, being asymptotically bounded by $n^{\frac{1}{9}}$.

In this work, we establish a connection between the cumulative residual entropy and the Gini mean difference (GMD). Some relationships between the extropy and the GMD, and the truncated GMD and dynamic versions of the cumulative past extropy are also established. We then show that several entropy and extropy measures discussed here can be brought into the framework of probability weighted moments, which would facilitate finding estimators of these measures.

This paper considers the first passage times to constant boundaries and the two-sided exit problem for Lévy process with a characteristic exponent in which at least one of the two jumps having rational Laplace transforms. The joint distribution of the first passage times and undershoot/overshoot are obtained. The processes recover many models that have appeared in the literature such as the compound Poisson risk models, the perturbed compound Poisson risk models, and their dual ones. As applications, we obtain the solutions for popular path-dependent options such as lookback and barrier options in terms of Laplace transforms.

We study 2-stage game-theoretic problem oriented 3-stage service policy computing, convolutional neural network (CNN) based algorithm design, and simulation for a blockchained buffering system with federated learning. More precisely, based on the game-theoretic problem consisting of both “win-lose” and “win-win” 2-stage competitions, we derive a 3-stage dynamical service policy via a saddle point to a zero-sum game problem and a Nash equilibrium point to a non-zero-sum game problem. This policy is concerning users-selection, dynamic pricing, and online rate resource allocation via stable digital currency for the system. The main focus is on the design and analysis of the joint 3-stage service policy for given queue/environment state dependent pricing and utility functions. The asymptotic optimality and fairness of this dynamic service policy is justified by diffusion modeling with approximation theory. A general CNN based policy computing algorithm flow chart along the line of the so-called big model framework is presented. Simulation case studies are conducted for the system with three users, where only two of the three users can be selected into the service by a zero-sum dual cost game competition policy at a time point. Then, the selected two users get into service and share the system rate service resource through a non-zero-sum dual cost game competition policy. Applications of our policy in the future blockchain based Internet (e.g., metaverse and web3.0) and supply chain finance are also briefly illustrated.

This article considers the individual equilibrium behavior and socially optimal strategy in a fluid queue with two types of parallel customers and incomplete fault. Assume that the working state and the incomplete fault state appear alternately in the buffer. Different from the linear revenue and expenditure structure, an exponential utility function can be constructed to obtain the equilibrium balking thresholds in the fully observable case. Besides, the steady-state probability distribution and the corresponding expected social benefit are derived based on the renewal process and the standard theory of linear ordinary differential equations. Furthermore, a reasonable entrance fee strategy is discussed under the condition that the fluid accepts the globally optimal strategies. Finally, the effects of the diverse system parameters on the entrance fee and the expected social benefit are explicitly illustrated by numerical comparisons.

This paper extends the standard double-exponential jump-diffusion (DEJD) model to allow for successive jumps to bring about different effects on the asset price process. The double-exponentially distributed jump sizes are no longer assumed to have the same parameters; instead, we assume that these parameters may take a series of different values to reflect growing or diminishing effects from these jumps. The mathematical analysis of the stock price requires an introduction of a number of distributions that are extended from the hypoexponential (HE) distribution. Under such a generalized setting, the European option price is derived in closed-form which ensures its computational convenience. Through our numerical examples, we examine the effects on the return distributions from the growing and diminishing severity of the upcoming jumps expected in the near future, and investigate how the option prices and the shapes of the implied volatility smiles are influenced by the varying severity of jumps. These results demonstrate the benefits of the modeling flexibility provided by our extension.

In this paper, we consider the friendship paradox in the context of random walks and paths. Among our results, we give an equality connecting long-range degree correlation, degree variability, and the degree-wise effect of additional steps for a random walk on a graph. Random paths are also considered, as well as applications to acquaintance sampling in the context of core-periphery structure.

We focus on exponential semi-Markov decision processes with unbounded transition rates. We first provide several sufficient conditions under which the value iteration procedure converges to the optimal value function and optimal deterministic stationary policies exist. These conditions are also valid for general semi-Markov decision processes possibly with accumulation points. Then, we apply our results to a service rate control problem with impatient customers. The resulting exponential semi-Markov decision process has unbounded transition rates, which makes the well-known uniformization technique inapplicable. We analyze the structure of the optimal policy and the monotonicity of the optimal value function by using the customization technique that was introduced by the author in prior work.

We consider the propagation of a stochastic SIR-type epidemic in two connected populations: a relatively small local population of interest which is surrounded by a much larger external population. External infectives can temporarily enter the small population and contribute to the spread of the infection inside this population. The rules for entry of infectives into the small population as well as their length of stay are modeled by a general Markov queueing system. Our main objective is to determine the distribution of the total number of infections within both populations. To do this, the approach we propose consists of deriving a family of martingales for the joint epidemic processes and applying classical stopping time or convergence theorems. The study then focuses on several particular cases where the external infection is described by a linear branching process and the entry of external infectives obeys certain specific rules. Some of the results obtained are illustrated by numerical examples.

Finite state Markov processes and their aggregated Markov processes have been extensively studied, especially in ion channel modeling and reliability modeling. In reliability field, the asymptotic behaviors of repairable systems modeled by both processes have been paid much attention to. For a Markov process, it is well-known that limiting measures such as availability and transition probability do not depend on the initial state of the process. However, for an aggregated Markov process, it is difficult to directly know whether this conclusion holds true or not from the limiting measure formulas expressed by the Laplace transforms. In this paper, four limiting measures expressed by Laplace transforms are proved to be independent of the initial state through Tauber’s theorem. The proof is presented under the assumption that the rank of transition rate matrix is one less than the dimension of state space for the Markov process, which includes the case that all states communicate with each other. Some numerical examples and discussions based on these are presented to illustrate the results directly and to show future related research topics. Finally, the conclusion of the paper is given.

We establish here an integral inequality for real log-concave functions, which can be viewed as an average monotone likelihood property. This inequality is then applied to examine the monotonicity of failure rates.

In this paper, we investigate the pricing of vulnerable European options in a market where the underlying stocks are not perfectly liquid. A liquidity discount factor is used to model the effect of liquidity risk in the market, and the default risk of the option issuer is incorporated into the model using a reduced-form model, where the default intensity process is correlated with the liquidity risk. We obtain a semiclosed-form pricing formula of vulnerable options through the inverse Fourier transform. Finally, we illustrate the effects of default risk and liquidity risk on option prices numerically.